Tent混沌和变邻域局部搜索优化的GSA

娄 奥，姚敏立，贾维敏，袁 丁

(1.火箭军工程大学 作战保障学院，陕西 西安 710025；2.火箭军工程大学 核工程学院，陕西 西安 710025)

智能算法又称“软计算”，是人们受自然界规律启迪，模仿其原理求解优化问题的算法。其中，群集式智能算法通过相互合作的简单个体搜索复杂问题的最优解，具有可扩充性好、实现简单等优点[1-2]。

引力搜索算法(Gravitational Search Algorithm, GSA)是伊朗科学家RASHEDI等[3]提出的一种新型群集式智能算法。有研究表明，当对基准函数测试时，引力搜索算法的全局搜索性能优于遗传算法、粒子群算法等其他智能算法[4]。但是，引力搜索算法存在易陷入局部最优、搜索精度有待提高等问题。为改善算法性能，文献[5]引入历史经验的思想，较好地提高了搜索精度；文献[6]基于进化程度和种群极值，设置自适应算子引导种群的搜索方向；文献[7]根据算法互补思想，设计新的粒子速度公式，也取得不错的实验效果。

笔者引入混沌和局部搜索思想优化引力搜索算法的全局寻优性能，提出一种Tent混沌和变邻域局部搜索优化的引力搜索算法(GSA optimized by Tent chaos and Variable neighborhood Local search，TVL-GSA)。首先设计一种遍历均匀性更好的Tent混沌模型初始化种群；再对粒子速度和引力系数进行改进；最后基于莱维飞行作变邻域局部搜索。

1 Tent混沌和变邻域局部搜索优化的引力搜索算法

1.1 引力搜索算法

引力搜索算法吸收牛顿第二定律的特点，赋予个体质量属性，使粒子之间存在吸引力。粒子的适应值越优，其质量也越大。粒子质量公式如下所示:

(1)

式中，t表示当前迭代次数，Mi,t是粒子i在t时刻的质量，fi,t是粒子i的适应值，wt是t时刻所有粒子的最差适应值，N是粒子总数。粒子i和j在第d维的引力大小的更新式为

(2)

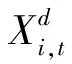
1.2 改进Tent混沌

文献[8]指出，利用Tent混沌的遍历性初始化种群，可以改善其分布均匀性，增强算法的全局搜索能力。但是，标准Tent混沌序列的相邻点有较强的相关性，易迭代到固有不动点而失去意义。为解决该问题，文献[8]提出一种分段式改进Tent混沌模型，不足之处是削弱了Tent混沌遍历均匀性强的优势。

笔者设计一种基于小随机附加项的改进Tent混沌模型，在避开固有不动点的前提下，尽可能维持Tent混沌的结构属性，保留其均匀性特征。改进Tent混沌的表达式如下:

(3)

式中，r是区间[0,1]内的随机数(下同)，T是最大迭代次数(下同)。取h=0.5，T=1 000，生成文献[8]和笔者改进的Tent混沌序列。序列分布直方图如图1及图2所示。

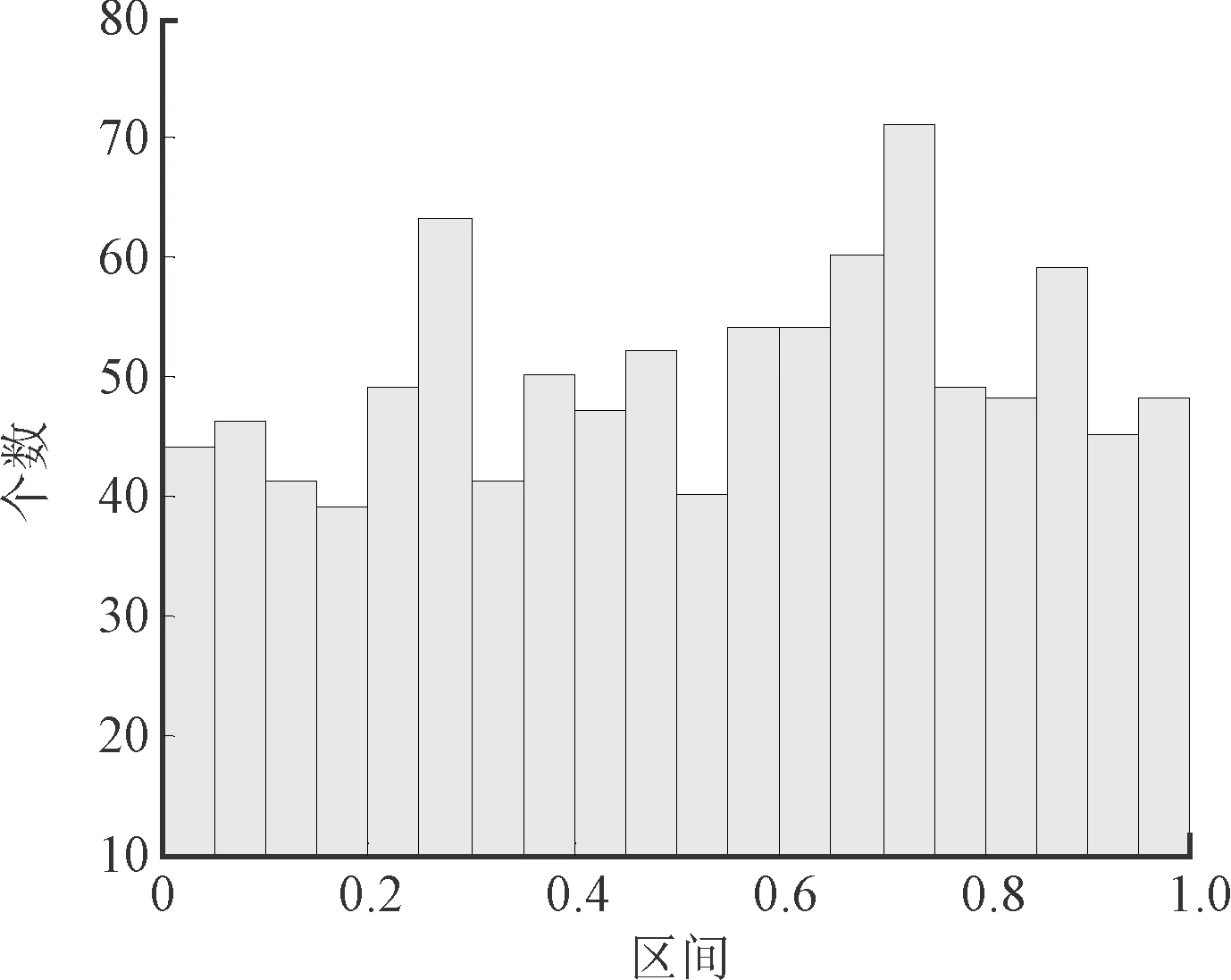
图1 文献[8]混沌序列分布直方图

图2 笔者改进的Tent混沌序列分布直方图

由图1和图2直观可见，两种混沌序列在[0,1]内各个子区间都有点分布，没有小周期和迭代归零的现象。而且，笔者改进的Tent混沌序列的点分布得更加均匀，遍历性更好。

1.3 基于莱维飞行的变邻域局部搜索策略

当求解多峰函数时，引力搜索算法的粒子一旦靠近局部峰值，极易因聚集效应驱使种群陷入局部最优。因此，对可能接近局部峰值的粒子作局部搜索，理论上可以抑制甚至避免种群落入局部最优陷阱的趋势。

(1)设种群第t次迭代后最优粒子的位置是Xb,t，对其作基于莱维飞行的局部搜索[9]:

(4)

式中，Xn b,t是搜索得到的新位置,Lβ是搜索步长。其中,μ～N(0,σ2)，ν～N(0,1)，1<β<3，o(Xb,t-1-Xb,t)是Xb,t-1和Xb,t的欧几里德度量,

(5)

(2)在式(4)中引入线性变化的惯性权重系数ω[10]。更新后公式为

(6)

其中，ωmax是最大权重,ωmin是最小权重，文中分别取其经验值1和0。

(3)计算Xn b,t的适应值。若其不小于Xb,t的适应值，则需要扩大邻域范围继续搜索。为式(6)添加邻域扩变系数γ：

(7)

其中，χ是区间[0,0.5]内实数。为控制成本，最多搜索3次。若找到更优解，则Xnb,t替换Xb,t。

1.4 改进粒子速度更新策略

引力搜索算法的速度公式为

vi,t=rvi,t-1+ai,t。

(8)

TVL-GSA在此基础上添加历史记忆信息，改进后公式为

.

vi,t=rvi,t-1+1.5ai,t+0.5(Xb,t-1-Xi,t-1),

(9)

其中，vi,t、ai,t是粒子i第t次迭代的速度、加速度；Xi,t-1是粒子i第t-1次迭代的位置。

1.5 改进引力系数公式

由式(2)可知,引力系数Gt与引力大小相关，会直接影响粒子移动(种群搜索)的速率。TVL-GSA为Gt增添系数d改变其下降速率:

Gt=G0(exp(-αt/T))d，

(10)

其中，G0是引力系数初值，一般取100;α是引力衰减系数，一般取20。d取不同值使Gt变化趋势差异较大，如图3所示。随着d值变大，Gt的下降加快，使引力搜索算法更早地进行精细搜索。这样的设计有利于单峰函数加速收敛到全局最优解，但也可能使多峰函数错过全局最优，陷入局部最优。为中和效果，d取经验值3。

1.6 TVL-GSA算法流程

TVL-GSA的主要思想包括3部分:第1部分，引入改进Tent混沌初始化种群，增加种群多样性，避免粒子在迭代早期就陷入局部最优;第2部分，改进引力搜索算法的速度和引力系数公式，对所有粒子完成引力搜索;第3部分，种群更新后，对最优粒子执行基于莱维飞行的变邻域局部搜索，引导种群脱离局部最优，并影响后续迭代中种群的搜索方向。

TVL-GSA的具体流程如图4所示。

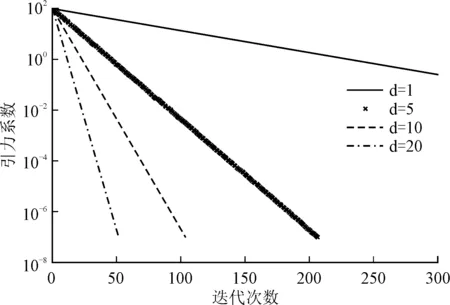
图3 引力系数变化曲线

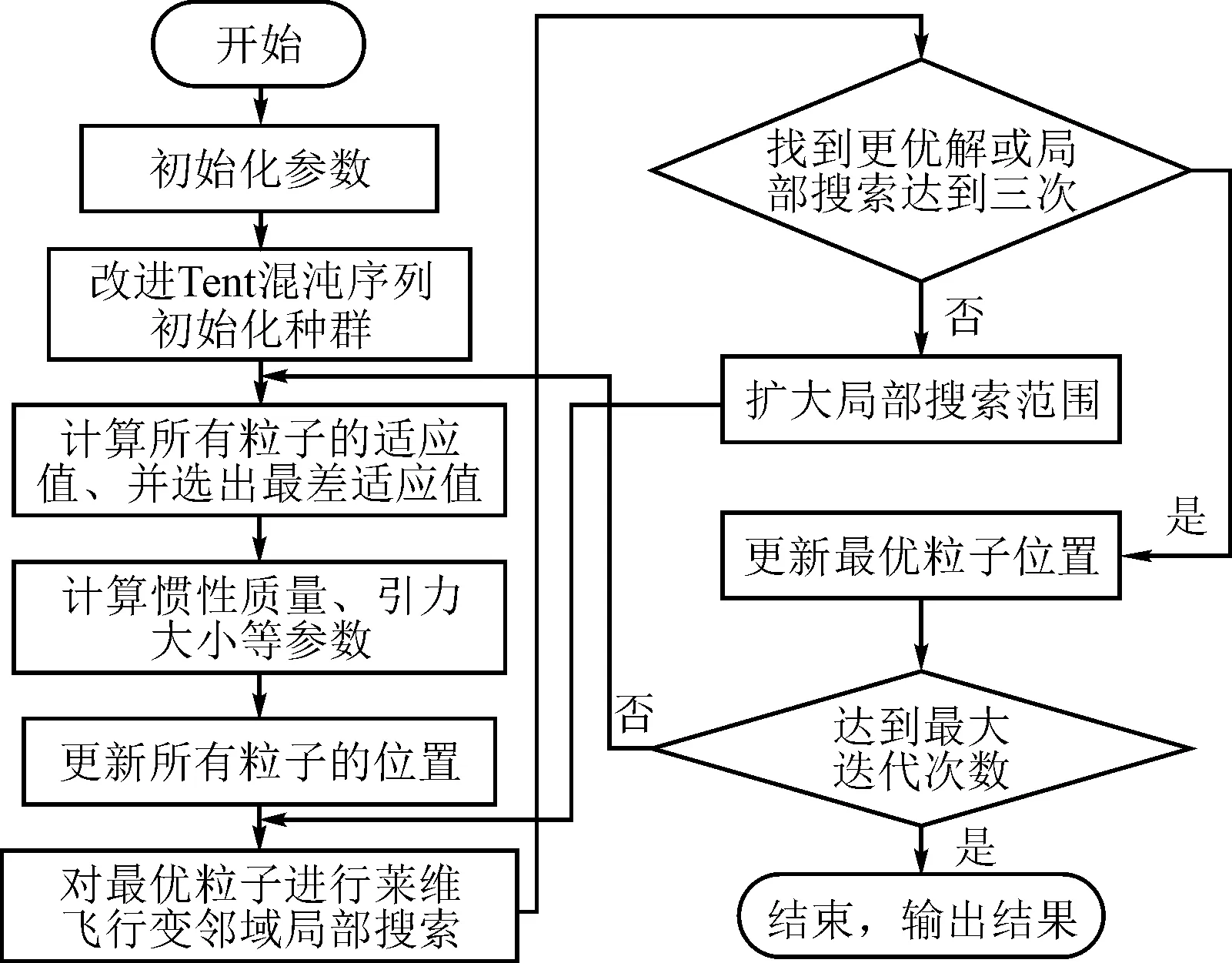
图4 TVL-GSA流程图

1.7 基准函数测试

在Intel (R)Core (TM)i3-2100 CPU@3.10 GHz，内存12.00 GB，Windows7系统和Matlab 2014b环境下做仿真实验。引入9个经典基准函数对GSA、I-GSA/PSO[5]、GGSA[6]、GPS[7]和TVL-GSA进行测试，函数说明如表1所示。

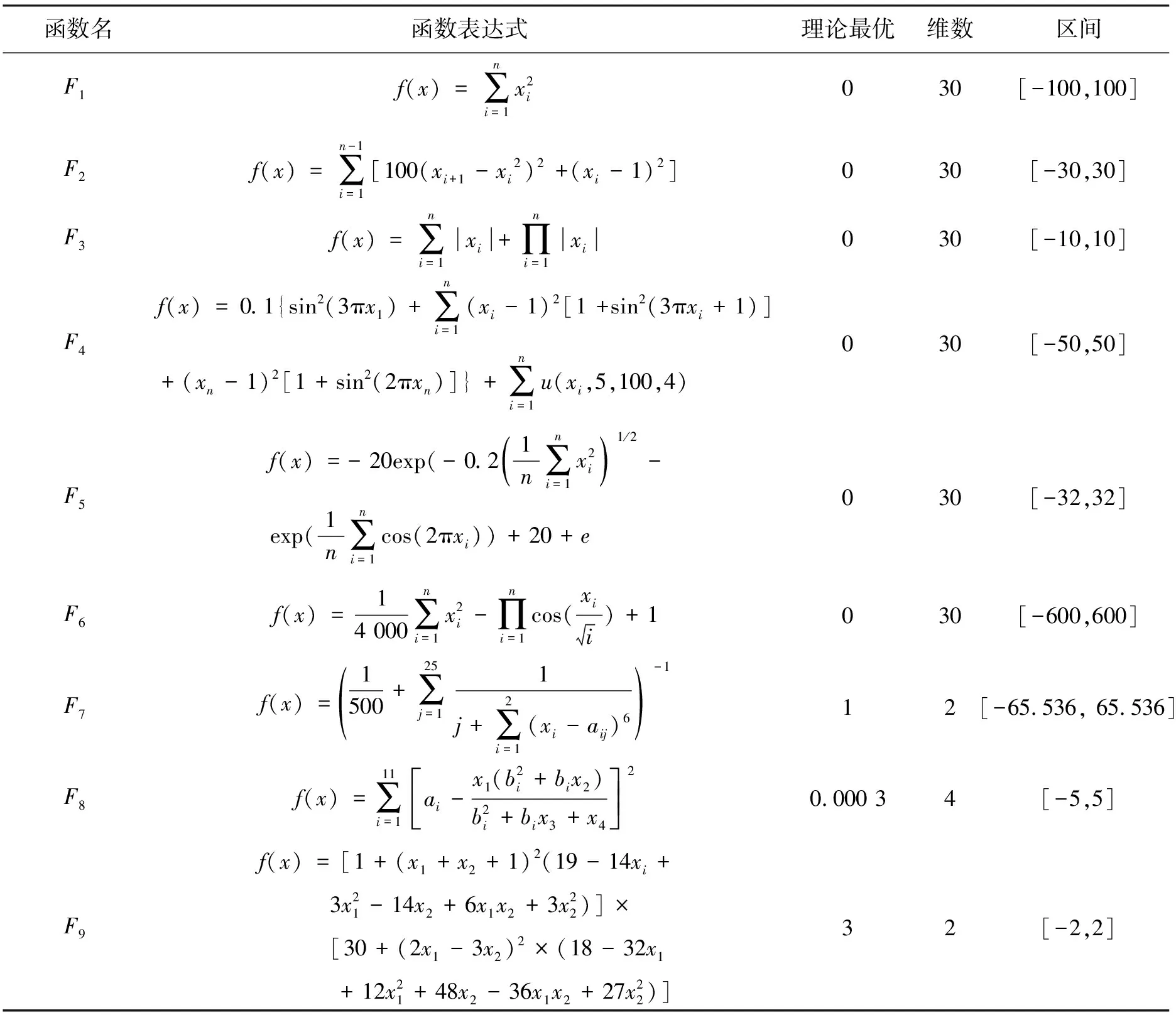
表1 基准函数说明

为减少误差影响，每个函数各测试20次，记录最优值、平均值和标准差，结果见表2。图5给出了算法对部分函数的迭代曲线(纵坐标是适应值的自然对数)。

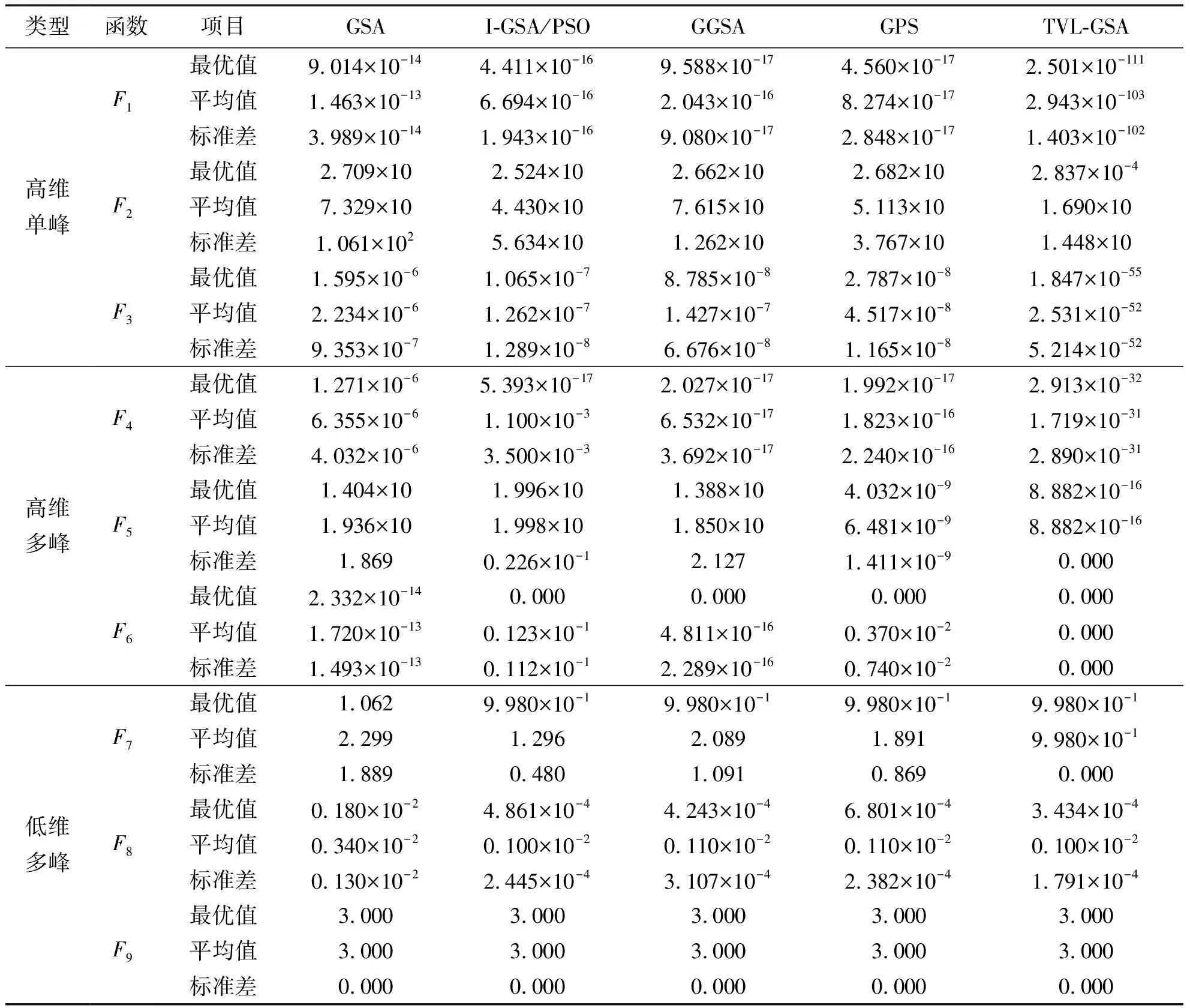
表2 函数测试结果

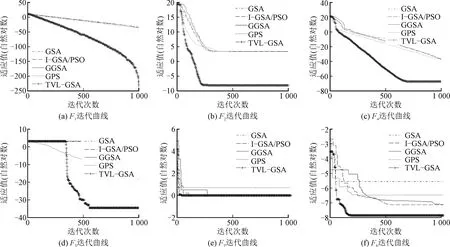
图5 算法对部分函数的迭代曲线

对于高维单峰函数F1～F3，TVL-GSA的寻优精度优于其他算法，展现绝对的优越性。以F1为例，TVL-GSA的均值比GPS等低86 ～ 90个数量级。图5中，TVL-GSA收敛速度也快于其他算法。

高维多峰函数有较多局部极值点，可以考查算法抑制局部最优的能力。表2中，TVL-GSA对F4～F6都取得较好的寻优效果。对于典型的非线性多模态函数F6，5种算法都得到其理论最优值0，但TVL-GSA的均值与标准差都最小。图5也显示TVL-GSA的收敛速度更快，付出的时间成本更少。

低维多峰函数的局部极值点较少，求解较易，但能检验算法的鲁棒性。表2中，TVL-GSA对F7～F9的指标均最小，且只有其对F7和F9的标准差均为0。这些数据说明TVL-GSA的全局搜索稳健性更强。

2 TVL-GSA对非线性系统辨识的应用

2.1 基于TVL-GSA优化径向基函数神经网络

径向基函数神经网络(Radial Basis Function Neural Network, RBFNN)是一种基于多变量插值径向基函数的神经网络，包含输入层、隐含层和输出层[11]。从模式识别角度看，非线性隐含层空间维数较高，能把低维非线性不可分问题映射到高维空间而线性可分[12]。因此径向基函数神经网络常用作辨识非线性系统的有效工具。

图6 TVL-GSA寻优径向基函数神经网络数据中心

隐含层径向基函数的数据中心是径向基函数神经网络的重要参数之一。工程中常用动态聚类算法，如K均值聚类对数据中心作自组织选择[13]。但是，K均值聚类存在对初始点敏感和全局搜索弱的缺陷，一定程度上会影响数据中心的选择结果。考虑到径向基函数的作用范围是局部的，不恰当的数据中心可能使径向基函数神经网络无法正确反映输入空间的实际情况，从而影响其逼近和泛化能力。上文证明，TVL-GSA有很强的全局寻优能力，将其与K均值聚类结合，理论上能弥补聚类的缺陷，提高数据中心的选择质量。TVL-GSA寻优径向基函数神经网络数据中心的策略如图6所示。

为检验优化后径向基函数神经网络解决实际问题的能力，以车载“动中通”伺服系统的非线性稳定环为对象，设计辨识实验。

2.2 辨识实验设计

动中通是一种在载体运动中实现不间断卫星通信的地球站[14]，其伺服系统采用四闭环(电流环、速度环、稳定环和位置环)体制。其中稳定环的作用是提高伺服系统抗载体扰动的能力，工程中得到其精确模型对闭环调节器的设计有重要的意义。但因工作时受摩擦阻力、惯性力矩、陀螺噪声等因素干扰，稳定环呈现明显的非线性特征。经典辨识方法已得不到稳定环的精确模型，可采用神经网络的辨识方法。

对0.9 m直径平板“动中通”的方位轴稳定环进行开环辨识。系统采用东方马达步进电机驱动，总减速比为425∶1;陀螺仪采用自制的微电机惯性测量单元。实验平台如图7所示。

辨识实验的具体步骤：首先保持稳定环为开环状态，为转台方位轴步进电机输入伪随机序列的激励信号(伪随机序列由10个移位寄存器生成，序列长度是210-1，幅值大小为2o/s)；然后从陀螺仪传感器采集转台空间角速度信息作为输出数据；最后利用优化后径向基函数神经网络辨识得到稳定环的开环模型。稳定环输出数据的采集流程如图8所示。

图7 动中通实验平台

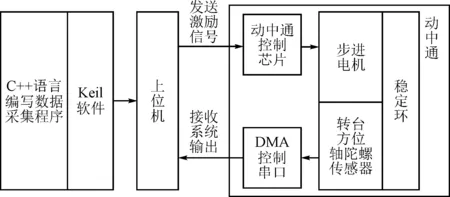
图8 稳定环输出数据的采集流程

2.3 辨识实验结果

采用标准反向传播神经网络(Back Propagation Neural Network, BPNN)、标准径向基函数神经网络和优化后径向基函数神经网络辨识稳定环。已通过节点删除法确定隐含层的最佳节点数为6。为保证实验有效性，各神经网络的隐含层节点数都相同。

实验1以稳定环输出的前1 200个数据为样本(为减少过渡过程的影响，再舍去前100个)，通过比较模型的精度，检验神经网络的逼近能力。结果如图9和图10所示。实验重复10次，记录模型的误差大小，如表3所示。

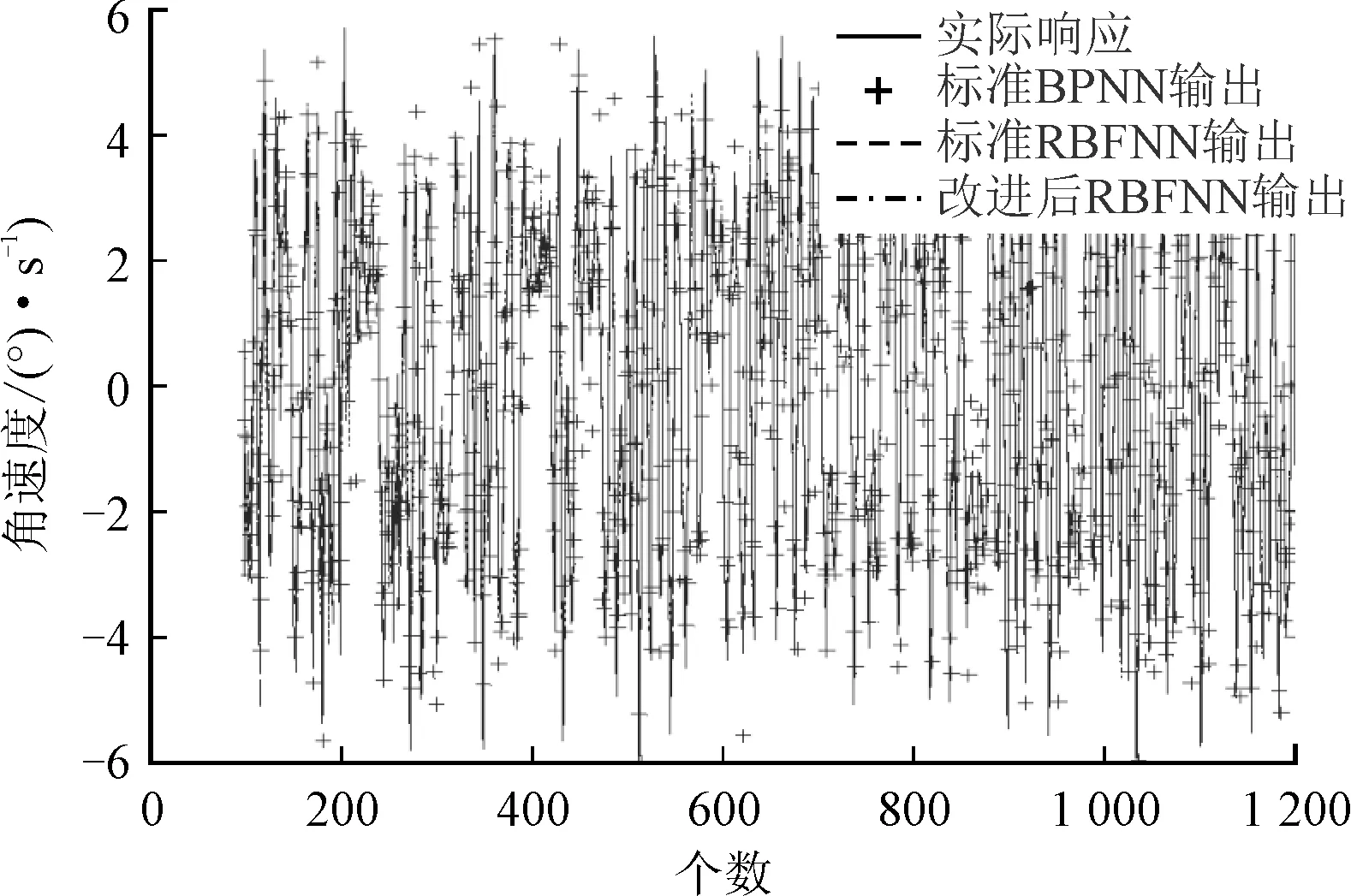
图9 不同神经网络的辨识结果

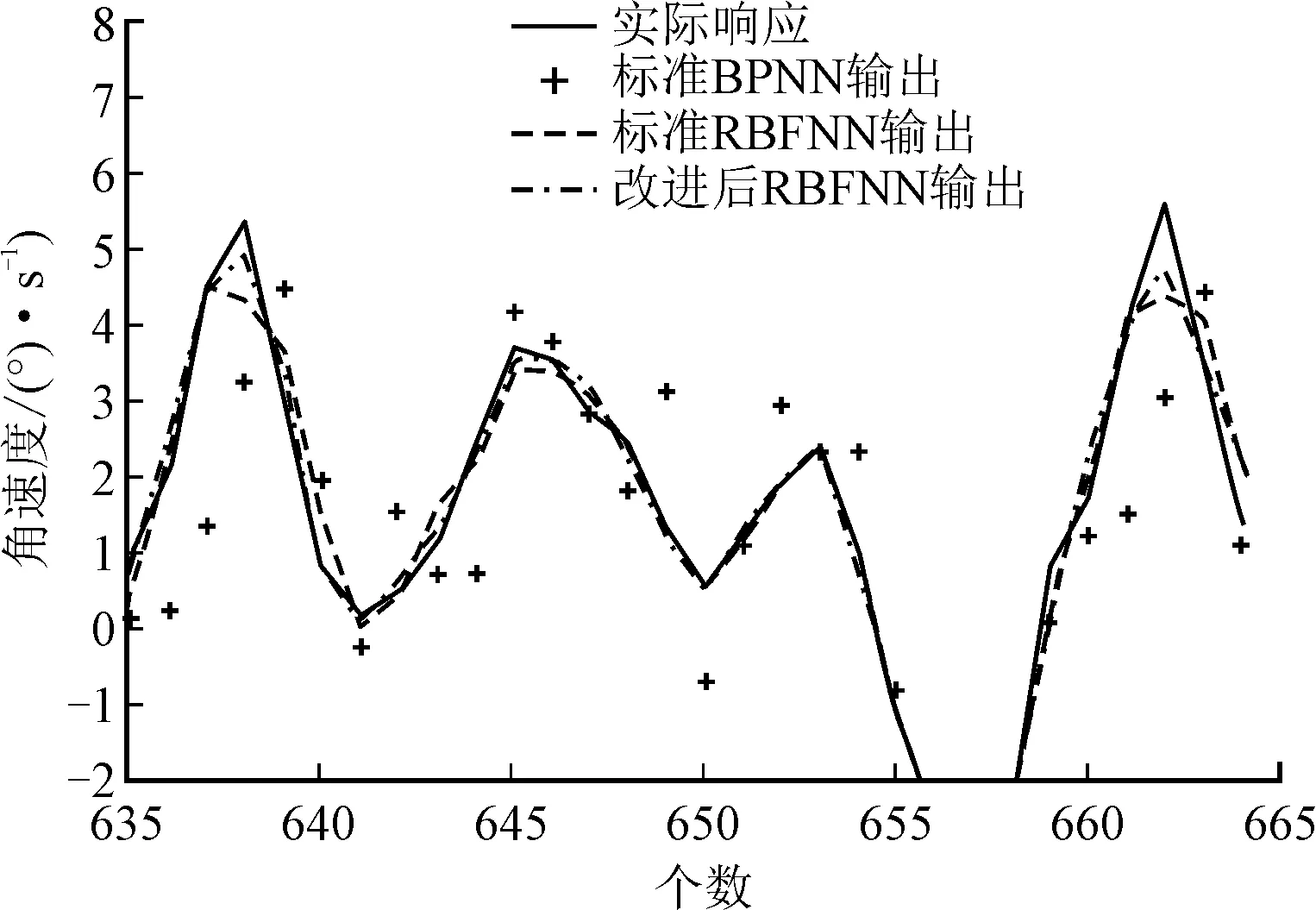
图10 不同神经网络的辨识结果(局部)

表3神经网络模型逼近误差

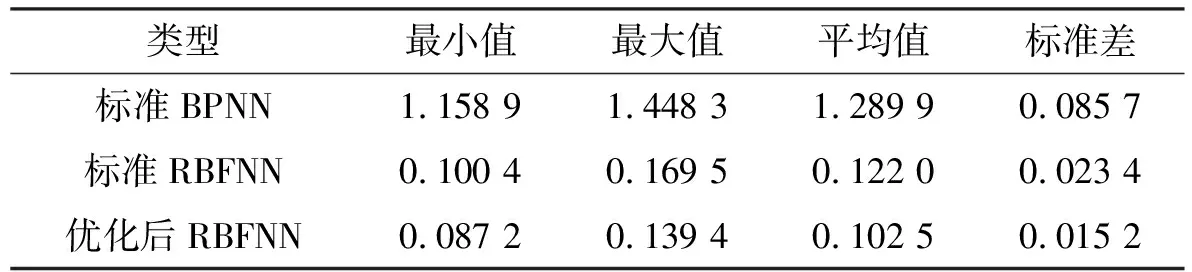
类型最小值最大值平均值标准差标准BPNN1.158 91.448 31.289 90.085 7标准RBFNN0.100 40.169 50.122 00.023 4优化后RBFNN0.087 20.139 40.102 50.015 2

由图10可见，标准反向传播神经网络的逼近误差很大，不能反映稳定环的实际输出。标准径向基函数神经网络受径向基函数作用，有较强的局部逼近能力。图10也证明标准径向基函数神经网络和优化后径向基函数神经网络的输出更接近实际响应。表3中，优化后径向基函数神经网络逼近误差的最小最大值、均值比标准径向基函数神经网络分别降低13.1%、17.8%和16.1%。

实验2取实验1得到的神经网络模型，拟合稳定环输出的第1 201至2 000个数据，检验神经网络的泛化能力。曲线拟合如图11和图12所示。实验重复10次，记录模型泛化的误差大小，如表4所示。

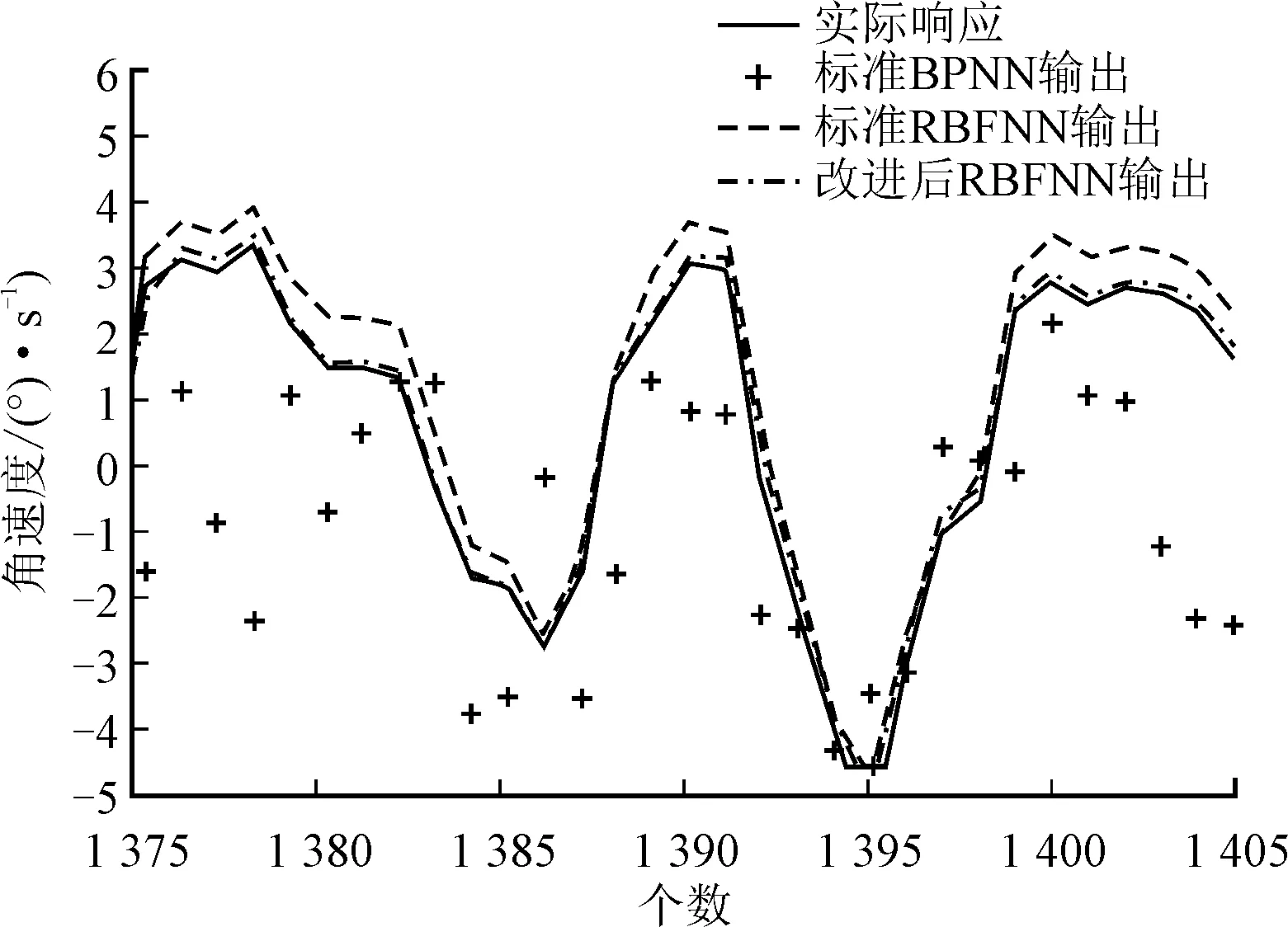
图12 不同神经网络的泛化结果(局部)

表4神经网络模型泛化误差

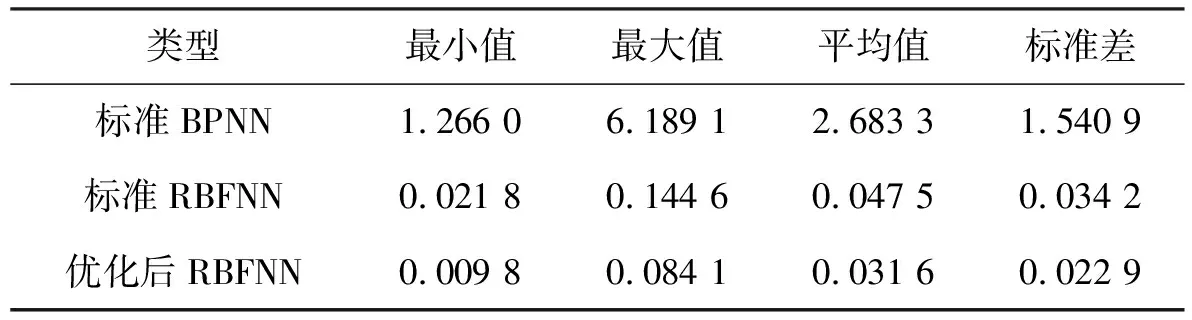
类型最小值最大值平均值标准差标准BPNN1.266 06.189 12.683 31.540 9标准RBFNN0.021 80.144 60.047 50.034 2优化后RBFNN0.009 80.084 10.031 60.022 9

由图12可知，标准反向传播神经网络的泛化能力极差，基本无法表征实际系统。标准径向基函数神经网络输出曲线的拟合程度较好，但当转台换向时误差变大。优化后径向基函数神经网络输出与系统输出几乎重合。结合表4数据可知，优化后径向基函数神经网络泛化误差的最小值、最大值和均值比标准径向基函数神经网络的分别降低55.0%、41.8%和33.5%。

3 结束语

笔者提出一种Tent混沌和变邻域局部搜索优化的引力搜索算法(TVL-GSA)。通过比较GSA、IGSA/PSO、GGSA、GPS、TVL-GSA的寻优性能，证明TVL-GSA能有效抑制局部最优，具备更佳的寻优精度和稳定性。利用TVL-GSA优化径向基函数神经网络，对车载“动中通”伺服系统的非线性稳定环进行辨识，结果表明其具有更优的逼近精度和泛化能力。下一步将设计径向基函数神经网络整定PID的控制系统，探索TVL-GSA更多的工程领域与应用价值。