基于SOM的电静压伺服机构油滤堵塞故障诊断
2019-11-08陈换过刘培君
俞 杭,陈换过,肖 雪,刘培君
(1.浙江理工大学 浙江省机电产品可靠性技术研究重点实验室,浙江 杭州 310018;2.北京精密机电控制设备研究所 事业部,北京 100076)
电液伺服机构因其良好的稳定性和高响应性,被广泛应用于航空航天领域.其中,电静压伺服机构(EHA, Electro-Hydraulic Actuator)作为一种新型的电液伺服机构,既具有与电机伺服机构(EMA, Electro-Mechanical Actuator)类似的电机驱动和控制功能,又具备高承载、易实现余度设计等突出优点,是当今伺服机构的主要发展趋势之一[1].但是,EHA是一个复杂的电、气、液系统,其故障呈现多样化和广泛性特点.其中,油滤堵塞故障是EHA相比于EMA特有的故障类型,也是EHA机构的薄弱环节.机构中双向油滤主要用来滤除系统油路中存在的固体杂质,降低油液的污染度,减少油腔内部的磨损,从而延长使用寿命.文献[2]研究表明,油滤堵塞会直接导致通油面积减小,流阻和节流损失增大而显著影响系统的响应速度.堵塞严重时还会造成油温升高,甚至导致液压部件的损坏.
目前,EHA的故障诊断技术尚处于起步阶段.WLAMIR等考虑喷嘴堵塞有关的失效模式,提出了一种利用衰落扩展卡尔曼滤波器进行系统辨识的伺服阀退化估计的方法[3];黄岳等基于执行器内部测点的数据变化,选用多元统计学方法对伺服机构执行器进行了故障诊断[4].SONG等从数学上推导了电液伺服机构油路泄漏和受摩擦影响的两种故障模型[5].肖雪等建立了伺服机构健康工况的主元模型,并依据油滤堵塞工况的平方预测误差统计量、Hotelling-T2统计量及其与健康阈值的对比状况,进行了故障诊断[6].这些研究主要针对的是伺服机构的液压泵、伺服阀等单部件.对于EHA的研究,目前还停留在性能分析与设计阶段,且在系统层面利用统计数据分析进行故障诊断的研究很不深入.由于伺服机构本身的复杂性和实际工况的多变性,伺服机构的信号随外负载而随机变化,信号不具有典型的频谱特征,导致特征提取十分困难,因此采用传统的故障诊断方法无法准确地反馈伺服机构的当前状态.
自组织映射网络,是一种无监督的学习方式,因此无需设置状态标签.它能够根据输入样本的分布,通过神经元之间的竞争选择获胜神经元,对输入模式进行分类,同时能够识别输入向量的拓扑结构,展现故障神经元之间的内部关联性.若将人工神经网络运用到EHA的故障诊断中,则可从数据处理层面进一步挖掘故障信息和特征,建立更为可靠、精确的故障诊断模型.
1 自组织映射神经网络
自组织特征映射网络(Self-Organizing Feature Maps, SOFM)又称自组织映射神经网络(SOM),最早由芬兰赫尔辛基理工大学的神经网络专家Kohonen于1981年提出[7],是一种竞争性神经网络,且具有自组织特性.
(1)设定变量.假设神经元输入样本为X=[X1,X2,…,Xm],每个样本包含m维向量;Wi(k)=[Wi1(k),Wi2(k),…,Wim(k)]为第i个输入节点与输出神经元之间的权值向量.
(2) 初始化.对输出层各权值向量赋值随机数,进行归一化处理,并建立初始优胜邻域Nj(0)和初始学习率η.
归一化的输入样本为:
(1)
式中,‖X‖为输入向量的欧几里得范数.
归一化的权值向量为:
(2)
式中,‖Wi(k)‖为权值向量的欧几里得范数.
(3) 输入随机样本Xi,寻找获胜节点,计算权值向量Wi(k)和样本Xi的内积,并使内积最大的输出神经元赢得竞争.由于样本向量和权值向量均已归一化,因此最小欧氏距离处即为内积最大处,也就是说,可将距离最小的那个神经元记为获胜神经元.神经元之间的距离为:
D(i,j)=‖X-Wi(k)‖
(3)
(4) 定义优胜邻域.以获胜神经元为中心,根据其权值调整域确定获胜区域.确定邻域时可采用不同的距离函数,如欧式距离、曼哈顿距离等.
(5) 调整权值.针对优胜邻域的所有节点调整权值,并采用Kohonen规则按下式进行更新.
wij(n+1)=wij(n)+η(xi(n)-wij(n))
=(1-η)wij(n)+ηxi(n)
(4)
式中:xi(n)为第i个输入神经元的值;wij(n)为邻域内神经元与xi(n)相连的权值.
在Matlab中,使用learnSOM函数,通过神经元输入样本X、激活率a2(i,j)和学习率lr,进行自组织映射神经网络的学习,并按下式进行权值ΔWi(k)的更新.
ΔWi(k)=lr·a2(i,j)·(X′-Wi(k))
(5)
式中,a2(i,j)由网络的输出值a(i,j)、神经元之间的距离D(i,j)及邻域大小Nd决定,即
(6)
(6) 当学习率衰减到某一预定值时,结束迭代.
2 仿真建模及数据分析
选取油滤堵塞类故障模式,并在AMESim系统中进行仿真建模.在AMESim系统中建立一个模拟飞控系统襟翼结构的电静压伺服机构仿真模型[8-10].系统在实际运行时,通过飞行控制计算机确定一个特定位置.电机通过泵的液压来推动作动器,从而移动襟翼来调整飞行姿态,完成指定动作.在仿真模型中,电机驱动液压泵旋转而提供系统流量,通过伺服驱动控制器调节电机转速、方向来改变系统的流量和方向,实现对作动器活塞杆伸缩和速度的控制,同时通过集成位移传感器,实现反馈闭环控制.
所建立的仿真模型为单通道电静压伺服机构.仿真时以指定脉冲信号作为输入信号,作动器最大位移为10 mm,并在9.523 s时施加1 500 N的外部负载.模型中各信号采集点的布置如图1所示.
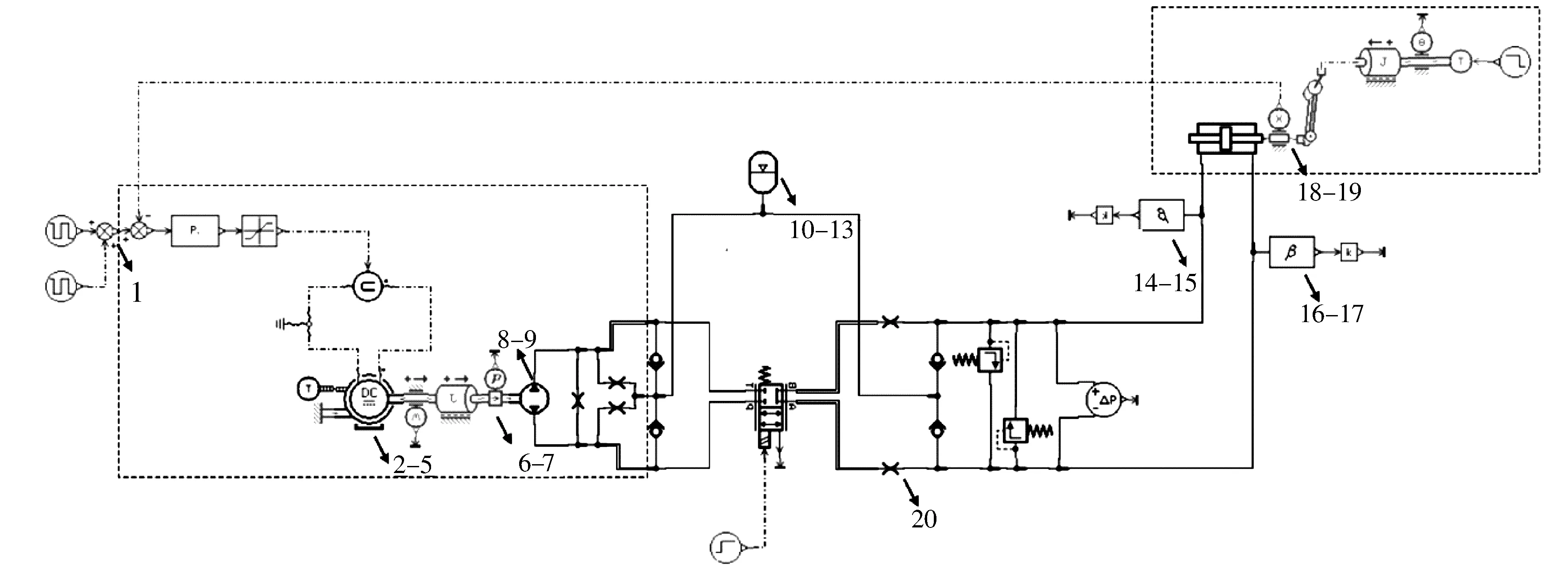
图1 模型中各信号采集点的布置
在仿真模型中,设置阻尼孔并改变其通径,以模拟不同程度的油滤堵塞故障工况.将阻尼孔(即油滤通油孔)的直径分别设为5.0 mm(健康工况)、3.0 mm、2.0 mm、1.5 mm、1.0 mm、0.5 mm.剩余通油面积百分比分别为100%、36%、16%、9%、4%、1%.系统仿真时间为20 s,采样频率为1 000 Hz.考虑到现实中传感器的布置特点及机构布置的合理性,选取作动器位移、电机电流和伸出腔油路压力这3个量进行信号采集.作动器位移曲线、电机电流曲线和伸出腔油路压力曲线分别见图2、图3和图4.
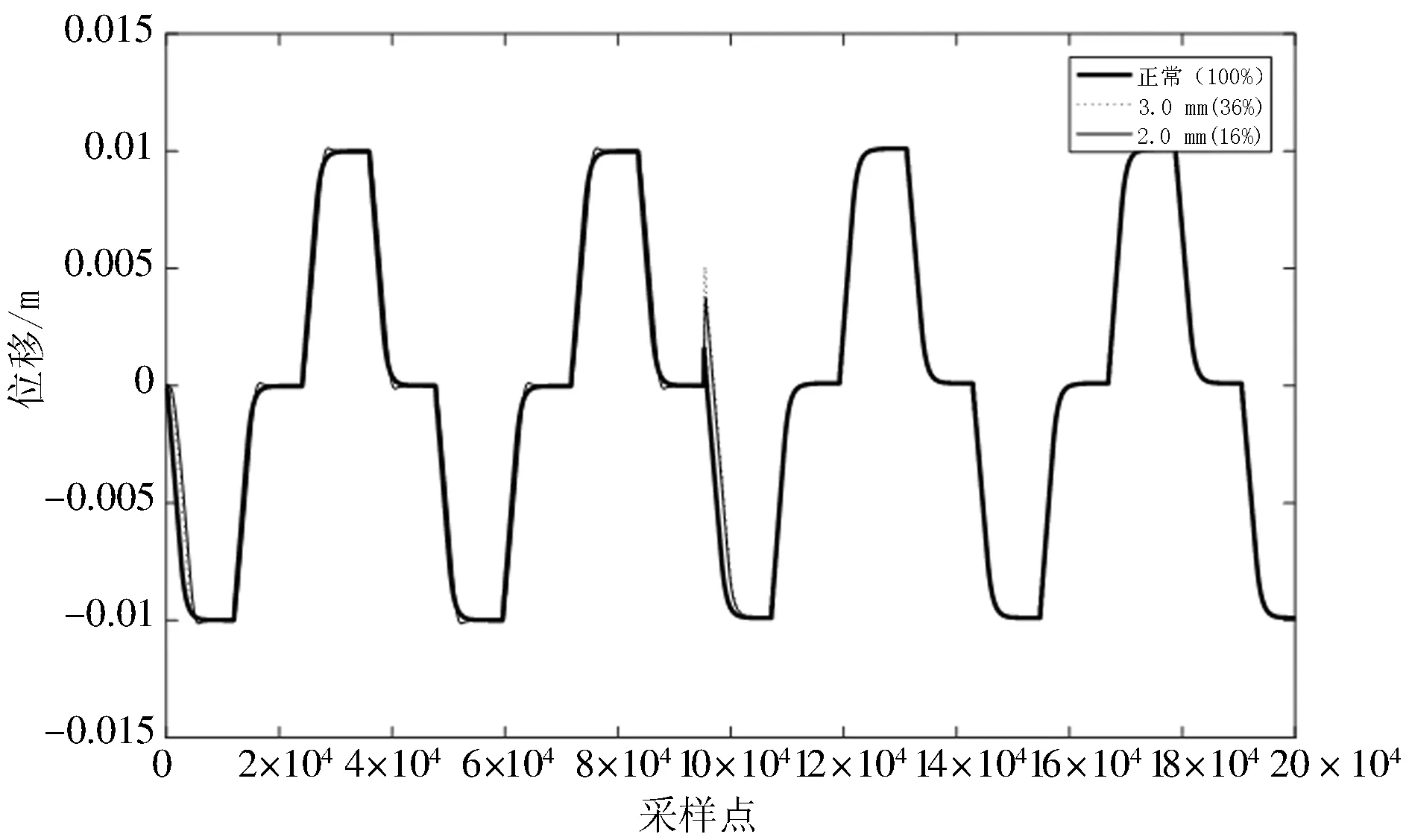
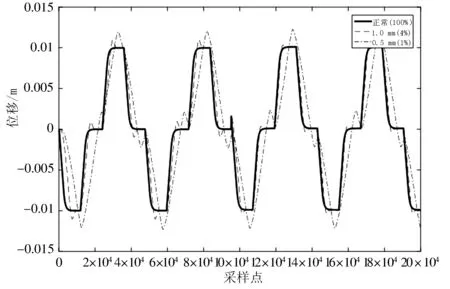
(b) 通油面积4%以下与正常情况
由图2~图4可知:在高负载情况下,当系统通油面积在16%及以上时,各测量曲线基本重合,无法直接判断系统状况;当通油面积下降到4%时,系统各参数的幅值随着通油面积的下降,出现剧烈变化,相比于正常工况差异较大,作动器出现明显的冲击、动作信号出现黏连,无法达到预定运行要求.对此进一步分析研究发现,在无负载下,系统的故障信息差别不大,但作动器位移信号随着通油孔径(即通孔直径)改变而发生变化的趋势更为明显.
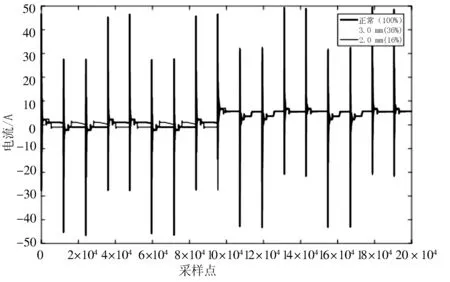
(a) 通油面积16%以上与正常情况
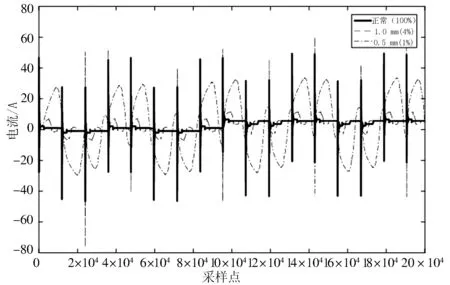
(b) 通油面积4%以下与正常情况
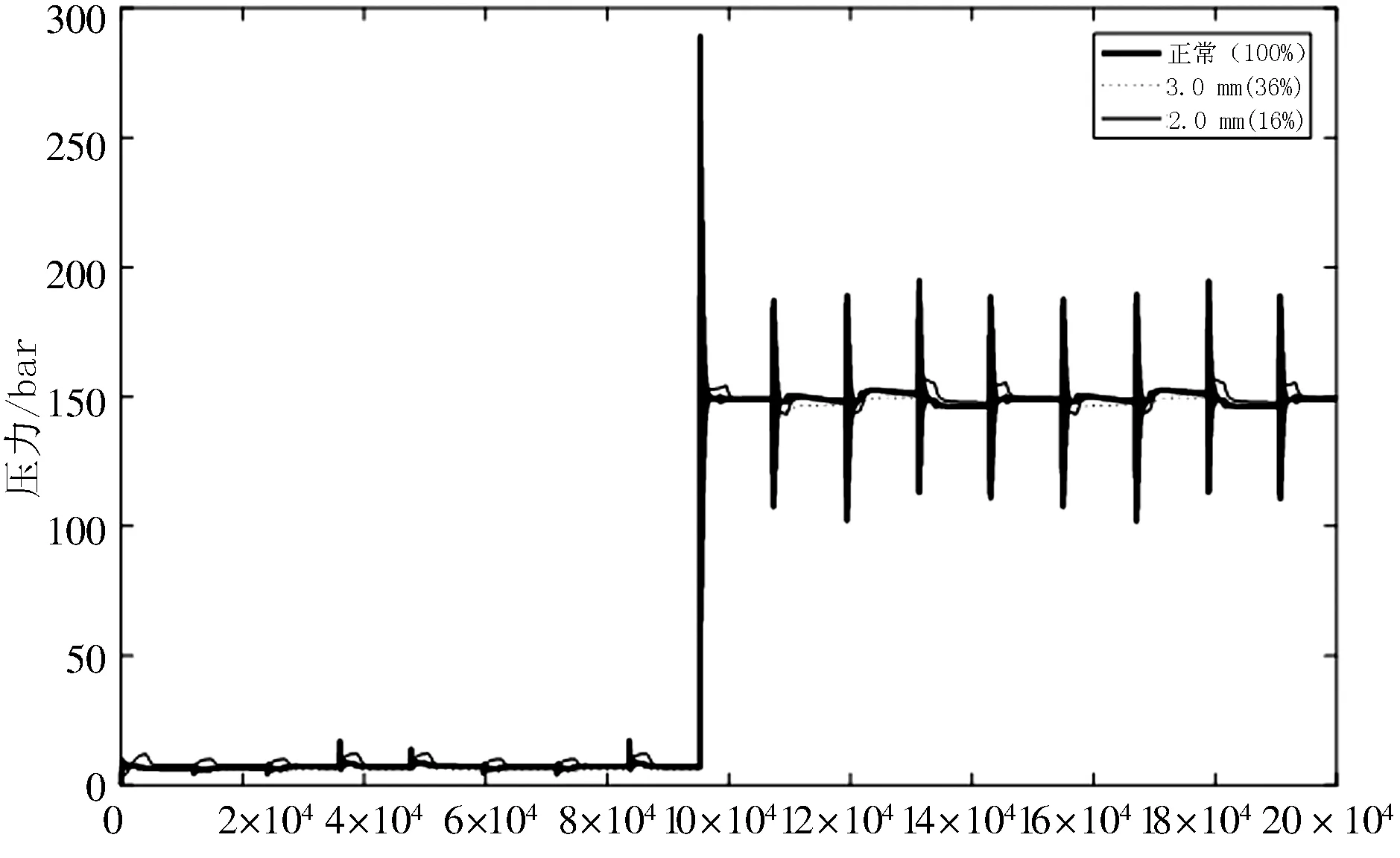
(a) 通油面积16%以上与正常情况
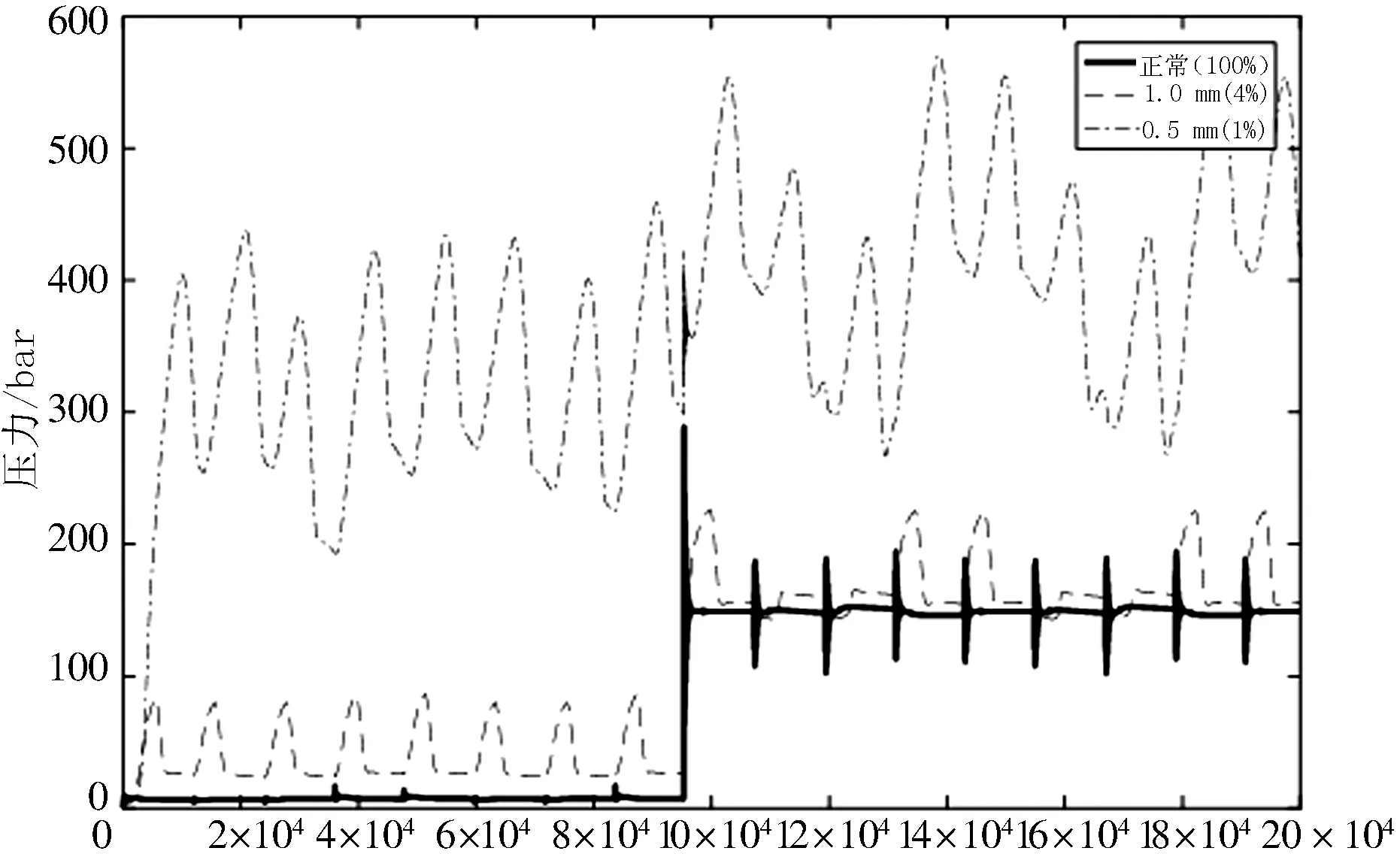
(b) 通油面积4%以下与正常情况
3 基于SOM模型的油滤堵塞故障诊断
3.1 仿真数据训练及测试
(1) 在AMESim系统中,选取7类以时间序列为故障样本的数据集(它包含正常状态1组,轻微堵塞和严重堵塞状态各3组).每个故障样本集中含有4组特征,分别是电机电流、电机转速、输出位移和输出速度.
不同油滤通油面积工况的测量值(又称特征参数)如表1所示.

表1 不同油滤通油面积工况的测量值
注:1.为简化表格,每个故障样本集只列举2个采样点的测量值;2.表中数据均已归一化处理,量纲为1。
(2) 选取通孔直径0.5 mm、1.0 mm、2.0 mm、3.0 mm、5.0 mm这5类状态作为训练样本,以通孔直径0.6 mm、2.5 mm,即通油面积1.44%、25%为测试样本,并设置神经元个数为10×10,训练步数为1 000.那么,应用SOM建立油滤堵塞故障模型的步骤如下:①选取故障样本;②对每种标准故障样本进行学习,学习后将具有最大输出的神经元作为该故障的标记;③将待检测样本输入SOM模型;④若输出神经元在输出层的位置与某标准故障样本的位置相同,则说明待检测样本发生了相应的故障;若输出神经元在输出层的位置介于很多标准故障之间,则说明这几种标准故障样本都有可能发生,且各故障发生的程度可根据该位置与相应标准故障样本位置的欧式距离来确定.
(3) 正常状态、轻微堵塞、严重堵塞这3种故障仿真数据的SOM神经元反馈分布如图5所示.

(a) 正常状态

(b) 轻微堵塞

(c) 严重堵塞
图5 3种故障仿真数据的SOM神经元反馈分布
从图5可看出:正常情况下,SOM神经元反馈分布在拓扑结构的中间区域,呈条状分布;轻微堵塞故障下,SOM神经元反馈呈随机分布,主要集中在拓扑结构的右端及左侧区域;严重堵塞故障下,SOM神经元反馈主要分布在拓扑结构的右端,呈半包围结构分布。
(4) 将测试样本0.6 mm、2.5 mm(指通孔直径)油路堵塞状态的系统特征参数输入SOM模型,可得图6所示的SOM神经元反馈分布情况。
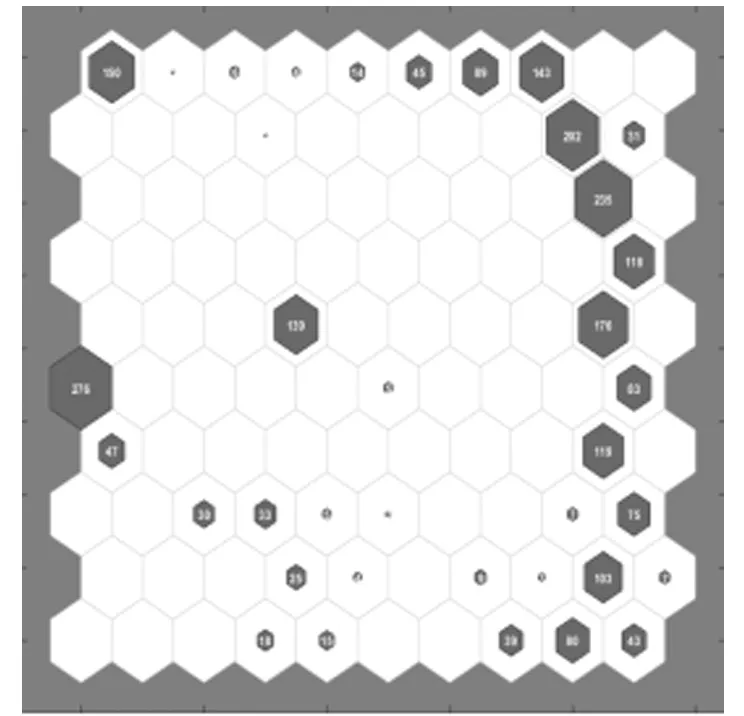
(a) 通孔直径 0.6 mm

(b) 通孔直径2.5 mm
图6 测试样本的SOM神经元反馈分布
图6与图5对比可知:在通孔直径0.6 mm(即通油面积为1.44%)状态下,SOM神经元的反馈分布与严重堵塞时情况一致;在通孔直径2.5 mm(即通油面积为25%)状态下,SOM神经元的反馈分布与轻微堵塞时情况一致.这与实际情况相符,表明了该方法的有效性.通常SOM模型的聚类运用往往针对单个神经元进行判断,本文以所有激活神经元的分布情况来判断故障程度,可大大减小采用单个神经元节点带来的误判风险,使结果更为直观.
3.2 实测数据训练及测试
搭建EHA试验平台,在空载荷下进行测试与分析[5].EHA样机的基本参数如表2所示.以通孔直径14 mm(即健康工况)作为参考,模拟油滤堵塞导致节流损失增大的故障工况,使通孔直径下降到6.3 mm,通油面积下降到78.29%,进行连续的位置指令阶跃信号测试.测试时间为0.5 s,采样频率为500 Hz,同时选取3个直接量(即作动器位移、电机转速和电机电流)对位移进行微分,得到作动器速度(这里称作间接量).以两种工况的3个直接量和1个间接量作为SOM模型的基本参数(表3),完成实测数据的训练.

表2 EHA样机的基本参数
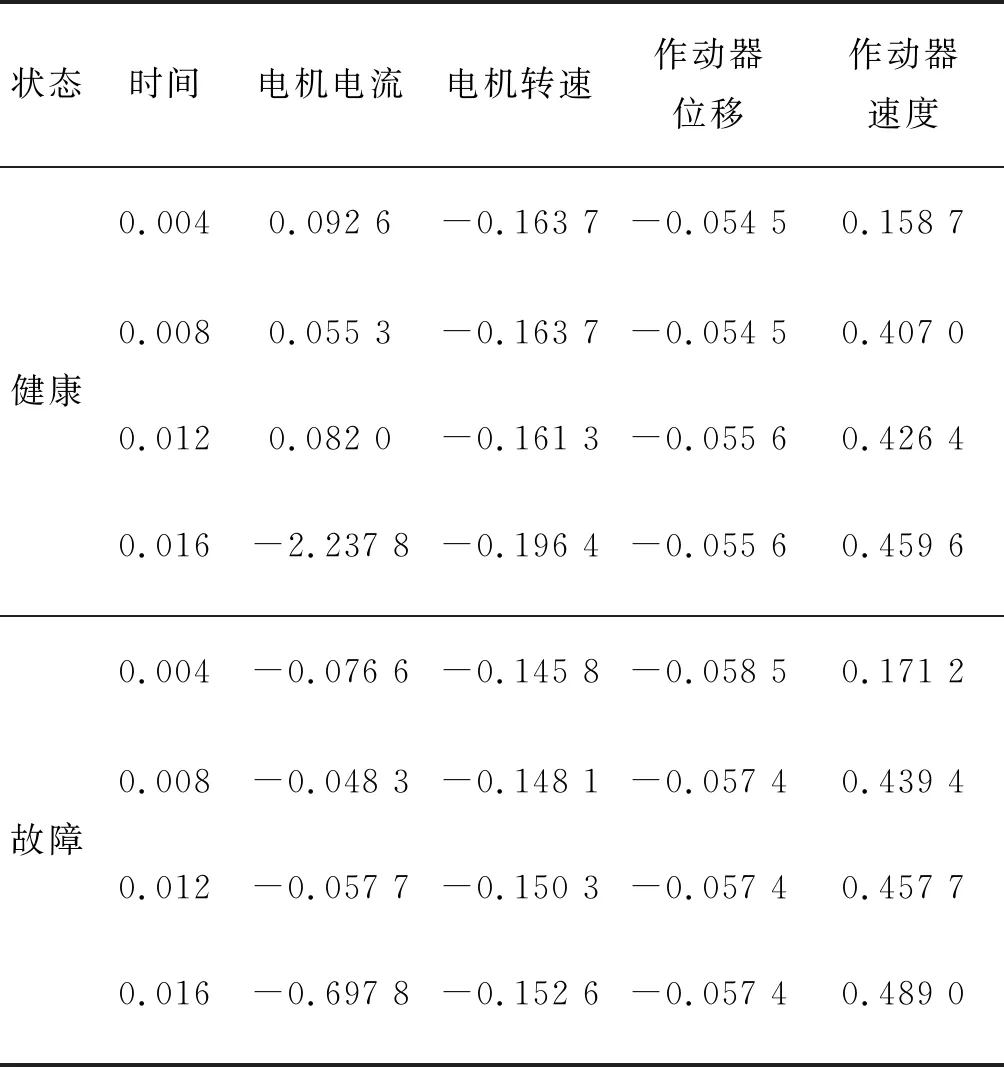
表3 SOM模型的基本参数
注:1.为简化表格,每种工况只列举4个采样点的测量值;2.表中数据均已归一化处理,量纲为1.
针对SOM模型,按照样本数量为460份(其中230份健康样本,230份故障样本),两种工况测试样本各20份,进行试验,可得图7所示试验数据的SOM神经元反馈分布情况.

(a) 正常状态激活神经元

(b) 故障状态激活神经元

(c) 正常状态输入测试
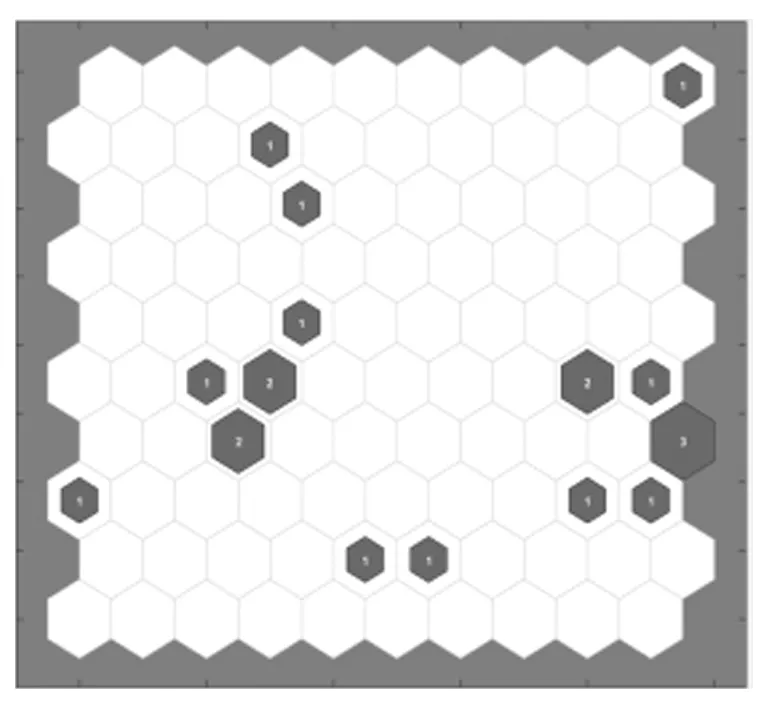
(d) 故障状态输入测试
图7 试验数据的SOM神经元反馈分布
观察图7可发现,将测试样本输入训练好的SOM模型,神经元的反馈分布与真实状态类似.这证明该方法是可行的.经过研究,该模型初步训练后,对正常状态的识别率可达80%,对故障状态的识别率可达90%.
4 结束语
通过仿真和试验数据的SOM模型搭建发现,SOM对于电静压伺服机构油滤堵塞故障诊断有良好的适用性,以神经元反馈分布作为故障程度判断的依据,比传统上依靠单个神经元来判断故障状态更为准确,在缺乏训练数据的情况下也可反馈当前状态.
尽管本文模型训练使用的数据点较少,且存在不可预测的测量噪声,使健康工况也有故障率,最后的反馈分布存在部分异常点,但这些异常点可通过后续加大训练样本量或者进一步优化训练模型得到消除.此外,基于SOM在电静压伺服机构油滤堵塞故障诊断方面的研究成果可应用于其他故障模式.
