一种可提高转矩输出能力的高速列车牵引电机方波工况单环弱磁控制策略
2019-11-08杨中平朱龙胜牟述佳
李 华,林 飞,杨中平,朱龙胜,牟述佳
(1.北京交通大学 电气工程学院,北京 100044;2.中车青岛四方车辆研究所有限公司,青岛 266000)
对于高速列车牵引传动系统,实现全速域高性能控制非常重要。鼠笼型感应电机以其结构简单、结实可靠的特点得到广泛的应用。当牵引电机在额定速度以下运行时,转子磁链一般保持在额定值不变,电机输出转矩可以完全由转矩电流控制。当电机运行在弱磁区时,由于电机电压受限,电机输出转矩随着速度上升而减小。此时,合适的弱磁控制策略显得十分重要,其可提高电机输出转矩和带载能力[1]。
弱磁控制的性能与转子磁链指令密切相关,但是牵引电机在高速区运行时,负载变化以及直流侧电压的扰动使得转子磁链指令难以计算,从而影响输出转矩[2]。最便于实现的是反比例弱磁控制[3-5],即转子磁链指令与电机转速成反比,但所需电压有可能超出逆变器的电压输出范围。文献[6-8]按照电机模型计算转子磁链指令,但电机参数的变化会导致控制效果不理想。文献[9-12] 通过逆变器最大电压与实际输出电压的误差作为电压控制器的输入,基于电压调节器得到励磁电流指令值,提高了弱磁控制策略的鲁棒性。文献[13]进一步分析对比了几种基于电压调节弱磁控制策略的优缺点。文献[14]采用离线查表法,励磁电流指令和转矩电流指令均通过查表得到。
以上所提弱磁控制策略都是采用PWM调制技术,而在大功率牵引传动系统中,在牵引电机进入弱磁区之后,通常会进入方波工况以充分利用直流母线电压并降低逆变器的开关频率[15]。在方波工况下,电机电压矢量幅值保持不变,传统矢量控制不再适合,因为传统矢量控制需要对感应电机定子电压的幅值和角度随时保持可控,方波工况下只有定子电压角度能够调节,如果仍采用传统矢量控制,会因两电流控制器相互冲突造成饱和,甚至影响电机正常运行。因此,弱磁控制策略需要考虑逆变器工作在方波模式下的情况。文献[16]在电机进入方波工况后不再采用双电流控制器,现有的部分高速列车也是采用类似电流开环控制方案,这种方法降低了电流的动态性能。文献[18-19]在文献[17]的基础上进一步考虑了方波工况时的限制条件和磁场定向问题。文献[20]针对于永磁同步电机,提出了一种新的基于交直轴电流耦合的单电流调节器控制策略,在弱磁区采用单电流控制器,交轴电压指令根据电机工况自行调节,该控制策略解决双电流调节器在电机高速域相互冲突而易于饱和的问题。
针对以上问题,本文在传统的双电流环矢量控制策略的基础上做了改进,针对方波工况下的特殊情况,在考虑直流侧电压、电流限制和负载变化的情况下,提出了一种新型电流闭环弱磁控制策略。该策略适合于方波工况,同时也可以保证电机在全速域转矩输出能力,提升方波工况下电流跟踪响应能力。最后,完成了所提出方波控制策略的实验验证。
1 感应电机数学模型及原理分析
在同步坐标系下,鼠笼型感应电机电压和磁链方程可以表示为
us=Rsis+jωeψs+pψs
ur=Rrir+jωslψr+pψr
ψs=Lsis+Lmir
ψr=Lrir+Lmis
(1)
式中:p为微分算子;us、ur分别为定、转子电压矢量;is、ir分别为定子、转子电流矢量;ψs、ψr分别为定子、转子磁链矢量;Rs、Rr分别为定子、转子电阻;Ls、Lr、Lm分别为定子电感、转子电感和互感;ωe、ωsl分别为定子、转差角频率。
对于采用鼠笼型感应电机的转子磁链定向控制系统,ur=0,ψrq=0,因此由式(1)可以可得

(2)
式中:usd、usq分别为定子电压d、q轴分量;isd、isq分别为定子电流d、q轴分量;σ为漏感系数;ωr为转子角频率。
在高速区时,稳态下d、q轴电压方程可以表示为
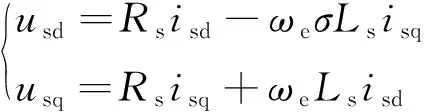
(3)
在同步坐标系下,电机转矩方程可以表示为
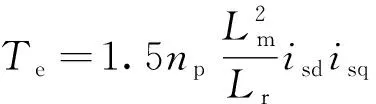
(4)
式中:np为极对数。
1.1 可调电压裕量对电流控制器性能的影响
矢量控制系统的信号流图如图1所示,即电流控制器的输出为电机的电压指令。

图1 矢量控制信号流图
由图1得,电流控制器可调电压裕量us_reg为
us_reg=Usmax-us
(5)
式中:us为定子实际电压;Usmax为逆变器可输出最大电压,取决于脉宽调制策略,方波下逆变器可输出最大电压为
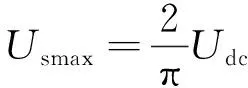
(6)
式中:Udc为直流侧电压。
随电机速度增加,感应电机的实际电压不断上升,逆变器调制比m增大,留给电流控制器可调节的电压越来越少,如图2所示,图中m1为临界调制比,其大小取决于控制策略、延时等因素。

图2 电流控制器可调节电压裕量和调制比的关系
当调制比m

表1 电流控制器调节性能与调制比的关系
由表1可得,当电机进入方波工况,采用双电流环矢量控制策略不再适合,需要对其进行改进,以满足方波工况的特殊的需求。
1.2 电流和电压限制下最大转矩输出
当感应电机运行弱磁区时,电机可输出最大转矩取决于定子电压和电流的限制。电机最大电压由逆变器直流侧电压和调制策略决定,最大电流由逆变器可输出最大电流和电机额定电流决定。因此,感应电机在弱磁区电流和电压限制表示为

(7)

(8)
式中:Ismax为电机可输出最大电流。
将式(3)代入电压限制方程式(7)可得
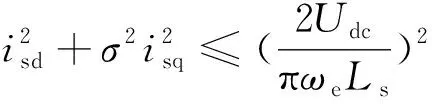
(9)
在isd-isq坐标系下,式(4)表示为一条双曲线,式(8)表示为一个圆,其半径只由电机可输出最大电流决定,式(9)表示为一个椭圆,其半轴由直流侧电压、电机参数和电机定子角频率决定,椭圆随着电机频率增加而逐渐缩小,如图3所示。显然,电机的电流矢量必须在电流限制圆和电压限制椭圆的公共区域运行。
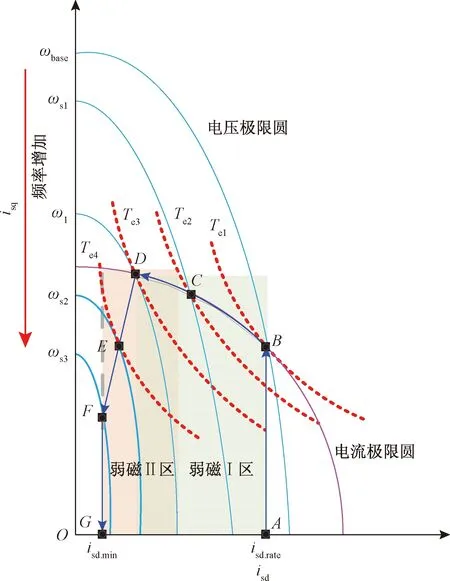
图3 isd-isq坐标系下电机限制条件
当电机在额定角频率ωbase以下运行时,此时电机电压还没有达到最大电压限制,只需要满足电流限制即可,对于高速列车来说,励磁电流isd一般给定为额定值isd.rate,而通过转矩电流isq来控制电机的转矩,因此,电机电流矢量运行轨迹为A→B。
当电机速度等于ωbase时,电机工作在B点,此时转矩电流达到最大值,电机输出转矩最大。同时,电压极限椭圆恰好穿过B点,因此电机电压也达到最大值。根据式(8)和式(9),可以求解得到
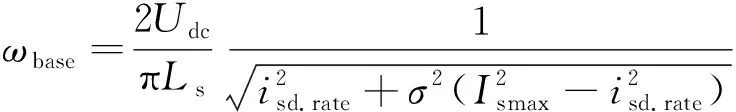
(10)
当电机速度超过ωbase后,电压限制椭圆继续缩小,电机定子达到最大电压限制条件。为了满足电机限制条件,励磁电流必须减小。由图1可得,当电机速度在ωbase和ω1之间时,电机输出最大转矩的电流矢量轨迹为B→D。
当电机速度等于ω1时,电机工作在D点。当电机速度继续升高时,为了充分利用逆变器输出电压,需要减小电机电流幅值,电机将不再工作在恒功率区,而是工作在恒电压区,一般称恒功率区为弱磁Ⅰ区,恒电压区为弱磁Ⅱ区,D为二者的临界点。
当电机速度超过ω1,电压极限椭圆继续缩小,此时只要满足电压限制就一定满足电流限制,为了输出最大转矩,根据式(4)和式(9),利用拉格朗日乘数法,可求得

(11)
根据式(11),可求解得励磁电流和转矩电流的关系为

(12)
当电机在弱磁Ⅱ区运行时,最大转矩输出电流运行轨迹不再是电流极限圆和电压极限椭圆的交点,而是转矩双曲线和电压极限椭圆相切的交点,即励磁电流和转矩电流满足关系式(12)。因此,当电机速度大于ω1时,电机输出最大转矩的电流矢量轨迹为D→F。同时,由式(11)、式(7)和式(8)可得,临界频率ω1为
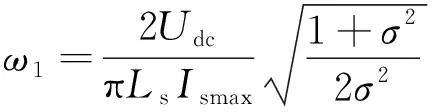
(13)
当电机速度继续增大,励磁电流减小到最小励磁电流isd.min时,将不能再减小,即速度大于ωs3时,电机电流矢量轨迹为F→G。以上分析可得电机在弱磁区最大转矩时电流矢量的运行轨迹。
1.3 d、q轴电流限制
由1.2节分析可得,牵引电机励磁电流isd一般不超过额定励磁电流isd.rate,同时为了保证电机正常工作,不能低于isd.min,因此,励磁电流需要满足

(14)

图4 牵引电机全速域矢量控制示意图
根据式(8)和式(12),可得转矩电流需要同时满足

(15)
2 方波单环弱磁控制
根据前对电机运行工况的理论分析,本文提出了牵引电机全速域矢量控制策略,如图4所示。当电机速度小于ωbase时,采用传统双电流环矢量控制策略,如图5所示。

图5 双电流环矢量控制示意图
当电机速度超过ωbase,进入方波工况,为了保证最大电压限制条件,采用单环控制策略,如图6所示。此时,q轴指令电压usq通过d轴电压指令值usd和最大电压Usmax计算得到。这样保证了电机在方波工况运行时,电压指令始终为在电压限制椭圆上,此时需要合理调节转子磁链,保证电流的动态性能。因此,弱磁控制器根据q轴电流误差来调节转子磁链,保证d、q轴电流分量的合理分配,使电流矢量在电流极限圆和电压极限椭圆的交点上运行。
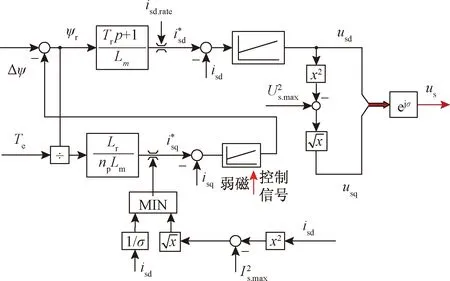
图6 方波单环弱磁控制策略
电机在进出方波时,能否实现平滑过渡,取决于良好的切换控制策略。当电机速度小于ωbase,d、q轴电压和最大电压限制关系为

(16)
当电机速度超过ωbase时,电机进入方波工况,电机电压达到最大电压限制。此时d、q轴电压和最大电压限制关系为
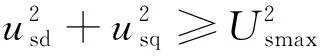
(17)

图7 切换控制策略示意图
2.1 可控性分析
电机控制的目的是准确而快速的输出期望的转矩。以恒速变载工况为例,分析电机控制。
根据式(3)和式(4),可得电机输出转矩在d、q轴电压坐标系下的表达式
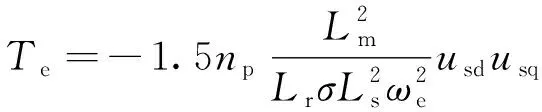
(18)

图8 负载变化时d、q轴电压变化情况

同理,负载转矩TL或者转速指令减小时,电机运行从B点向A点移动。
2.2 弱磁控制器设计
在进入方波工况前,电压usq控制来控制转矩电流isq,而进入方波工况后,isq不再是通过q轴电压usq控制,因此如果把usq看作扰动,由式(1)可得isq和isd表达式

(19)
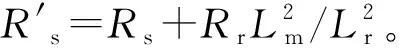
可得励磁电流和转矩电流的传递函数示意图,见图9

图9 励磁电流和转矩电流的传递函数示意图
因此,可得其开环传递函数为

(20)
采用串联工程设计方法来确定控制器参数,可令1+sTd≈sTd,传递函数可以简化为

(21)
式中:τ=kp/ki。
采用三阶最佳设计法得控制器参数为

(22)
3 实验结果分析
基于中车青岛四方车辆研究所的CRH5型车实验平台,对全速域矢量控制算法进行了实验验证。实验平台采用CRH5型车动车组实际的牵引控制器(TCU),通过dSPACE仿真器来模拟牵引传动系统的特性和外部环境。
牵引电机采用CRH5型车国产化电机参数,实验平台参数见表2。牵引电机转矩和磁链指令按照CRH5型车电机特性曲线给定。算法中坐标变换采用等幅值原则,牵引电机定子电压幅值最大值Vsmax为2 292 V。
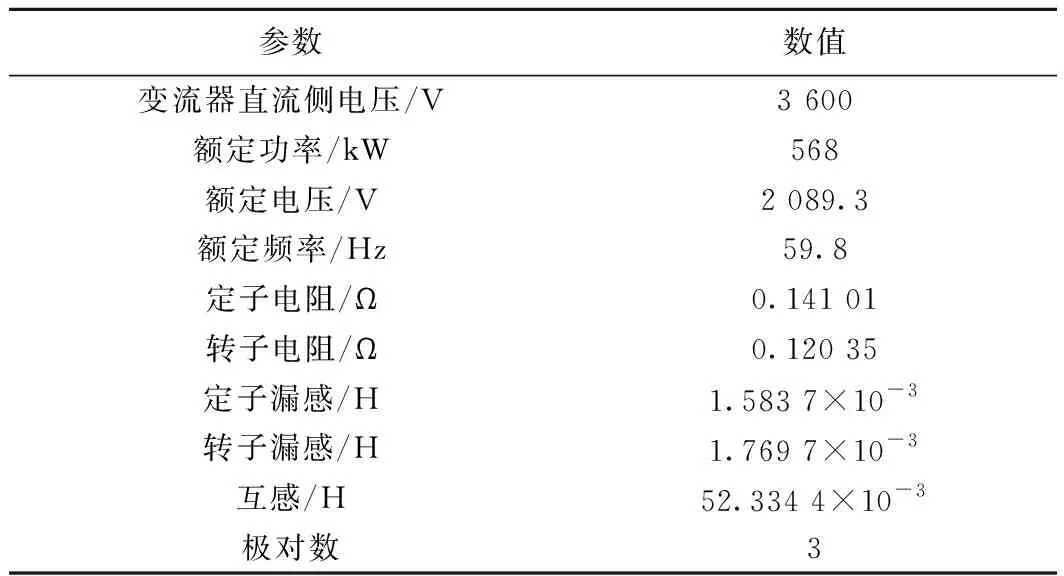
表2 牵引电机实验平台参数
通过上位机控制电机从600 rad/min加速到3 200 rad/min,转速和相电流波形如图10所示,d、q轴电流波形如图11所示,电机进入方波时d轴电流跟踪情况、相电流波形和相电压脉冲的波形如图12所示。在恒转矩区,电机电流幅值保持不变,励磁电流isd等于额定值isd.rate。当电机进入恒功率区且电机电压还没有达到逆变器可输出最大值时,电机电压随着速度增加而上升。为保持恒功运行,相电流幅值随着速度上升而减小,此时转矩和磁链指令都随着速度上升而减小,d、q轴电流也相应的减小。当电机进入方波工况时,电机电压幅值保持最大值不变,此时方波单环弱磁控制算法生效,为提高转矩输出,励磁电流isd随速度上升而略有减小,相电流的幅值基本不变。
由图11可以看出,电机进入方波工况时,实际d、q轴电流始终与指令值保持一致。由图12可知,相电流和d轴电流在电机进入方波切换算法时没有冲击,这也验证了本文所提出的切换策略的有效性。

图10 转速和相电流波形

图11 d、q轴电流跟踪情况
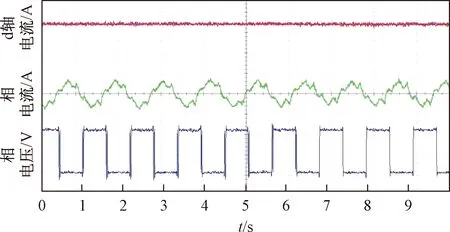
图12 进入方波时相电压脉冲和电流波形
图13为电机从600 rad/min加速到3 200 rad/min时,相电压幅值和弱磁控制器输出波形。图14为d、q轴定子电压波形。在电机未进入方波工况时,d、q轴定子电压绝对值随着速度上升而增大,相电压不断增加,此时,弱磁控制器不起作用。当电机进入方波工况以后,电机电压达到逆变器可输出最大电压,弱磁控制器作用,励磁电流isd减小,从而使q轴电压usq不再随着速度上升而增大,电机电压us维持在逆变器可输出最大电压。
图15为采用本文所提出方波单环弱磁控制和传统反比例弱磁控制电机输出电磁转矩对比。可以看出,当牵引电机在弱磁区运行时,采用本文所提出控制策略相比于传统反比例弱磁控制电机输出转矩有了明显的提升,平均提升转矩6.5%。
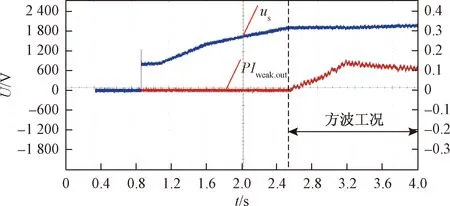
图13 定子电压和弱磁控制器输出波形
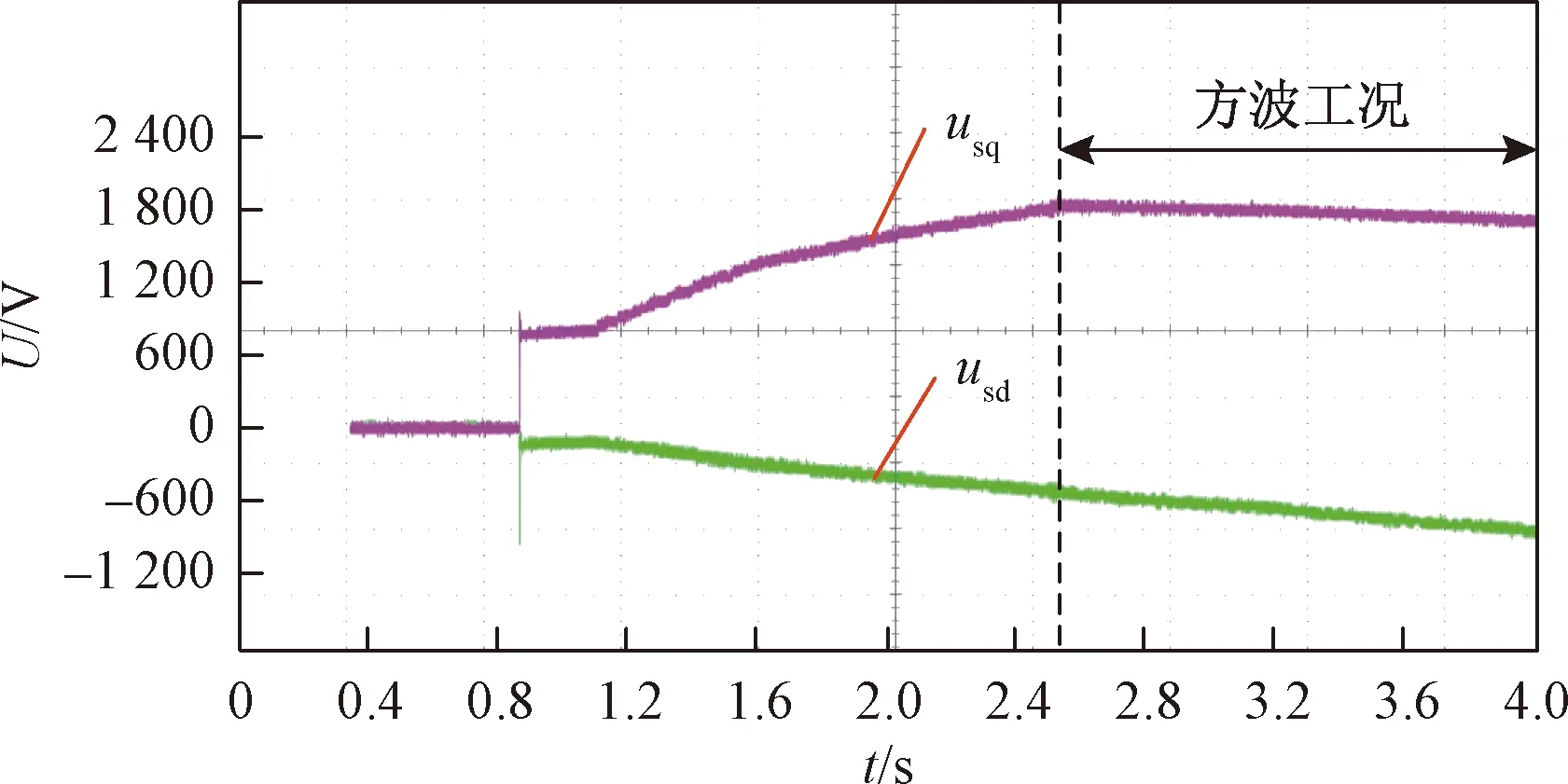
图14 d、q轴定子电压波形

图15 牵引电机在不同速度下转矩输出
图16和图17分别为牵引电机在方波工况下以恒速2 600 rad/min运行转矩指令突变时,d、q轴电流和相电流瞬态响应波形。转矩指令从2 000 N·m阶跃到2 400 N·m,再减小到1 600 N·m,可以看出励磁电流和转矩电流动态响应迅速。

图16 方波工况转矩指令突变时d、q轴电流响应

图17 方波工况转矩指令突变时相电流波形响应
4 结论
本文针对大功率高速列车牵引传动系统,分析了牵引电机在方波工况下的转矩输出与电流、电压限制的关系,根据电机数学模型得到了isd-isq坐标下最大转矩输出时最优电流矢量轨迹,并基于此提出了一种适合于方波的单环弱磁控制策略,并在CRH5型车电机控制实验平台完成了实验验证。本文主要得到如下结论:
(1)在方波工况下,电机定子电压的幅值不变,传统矢量控制不再适合方波工况。
(2)本文所提控制策略完全满足于方波工况电机限制条件,且在进出方波时没有冲击,可实现平滑过渡。
(3)相比于传统的反比例弱磁控制策略,采用本文所提的单环弱磁控制策略,电机转矩输出提升6.5%。
(4)本文所提弱磁控制在电机转矩指令突变时,电机d、q轴电流跟踪响应快速,保证了电机输出转矩准确而快速跟踪转矩指令。
