高速列车牵引传动系统机电耦合振动及其影响因素分析

2019-11-08赵心颖杨中平李翔飞张志强焦京海

铁道学报 2019年10期

赵心颖,杨中平,林飞,李翔飞,张志强,焦京海

(1.北京交通大学电气工程学院，北京 100044；2.中车青岛四方机车车辆股份有限公司，青岛 266000)

在高速列车运行过程中，牵引传动系统电气部分将把接触网传递过来的单相交流电，转换为适合牵引电机的可变频率和幅值的三相交流电，从而驱动电机转动，而机械部分是负责将电机转矩通过齿轮箱、联轴节等弹性环节传递到轮对，最终牵引列车稳定运行[1]。

高速列车传动装置工作环境恶劣，工作时会承受较大的冲击。在运行过程中，各个部件会因为弹性形变而产生不同程度的瞬时转速起伏，形成沿旋转方向的来回扭动，从而产生轴系扭转振动。在高速列车运行过程中，各部件振动等现象普遍存在，会增加轴的疲劳损伤，降低其使用寿命[2-4]。

目前，仅从机械结构和轮轨耦合两方面对传动装置振动进行研究[5-6]，但随着PWM逆变器的使用，电气激励对振动的影响也逐渐受到了关注。荷兰学者Winterling等[7-9]简单分析了电机的谐波转矩特性以及两者的耦合关系，但未进行实验验证。文献[10-11]建立了转向架和车体系统模型，研究了电机转矩脉动作用下的架悬式驱动装置振动。文献[12-13] 用双惯量模型对电机-负载系统进行建模，发现负荷冲击或者阶跃输入会造成系统产生固有频率下的振动。但大多数对于电气控制和振动机理方面的研究较浅，并且没有考虑驱动装置各部件的振动情况。

为了便于分析，通常将轴系振动分成弯曲振动和扭转振动，弯曲振动的表现形式是垂向和横向振动，而扭转振动主要是角速度和角加速度的波动。实际上二者是相互耦合的[14-15]，对扭转-弯曲振动之间的耦合关系进行深入研究是研究机电耦合振动必不可少的一环。

本文从电气与机械耦合关系出发，建立了高速列车传动系统模型，从谐振频率和根轨迹的角度解释了产生机电耦合振动的根源，对机电耦合振动现象及电气量影响作用进行了深入分析，将系统的电气振荡转化为机械振动，且进行了仿真和实验验证。

1 牵引传动系统扭转振动分析

1.1 双惯量模型

为了对传动系统稳定性进行深入分析，本节首先将机械结构简化为主动和从动装置结构组成的双惯量模型，如图1所示[16]。

电机转矩Tm作为输入激励，根据胡克定律和力学分析可建立驱动微分方程组[17]

(1)

式中：Jm、Jl为电机侧、负载侧转动惯量；C为阻尼系数；K为扭转刚度；θm、θl分别为主动、从动装置的角位移；Tl为负载转矩。

对式(1)进行拉普拉斯变换，可得双惯量系统传递函数模型为

(2)

(3)

式中：ωp、ωz为谐振、抗谐振频率；ξp、ξz为谐振、抗谐振阻尼。

电机输出转速、负载转速与电机转矩的传递函数如图2所示，其由惯性环节和二阶振荡环节组成，二阶振荡环节在复平面中引入了一对共轭复根极点，频率值为ωp。

图2 双惯量系统传递函数模型

阻尼系数ξp一般很小，因此可以忽略。由图3所示波特图可得，该模型存在一个谐振频率点和一个抗谐振频率点。谐振频率主要由刚度K和转动惯量Jl决定：K越大，ωp越大；Jl越大，ωp越小。

图3 双惯量波特图分析结果

式(2)对应的传递函数系统增益在谐振频率点(约21.3 Hz)处急剧增加，而式(3)中负载转速相位在谐振点处也会发生大幅度变化。若系统带宽包含谐振频率，外界干扰可能会导致驱动装置产生振动。

1.2 系统稳定性分析

高速列车牵引传动系统实际采用电机矢量控制，其电流环响应速度很快，因此可将电流环简化成时间常数为τ的一阶惯性环节，包含机电耦合因素的控制框图见图4。

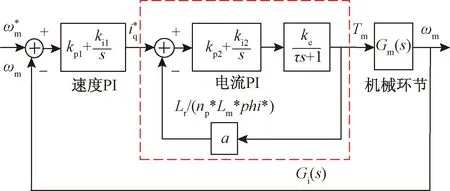
图4 牵引传动系统理论模型

系统开环传递函数为G(s)，由机械结构Gm(s)、电能变换环节G1(s)和速度调节3个部分组成，即

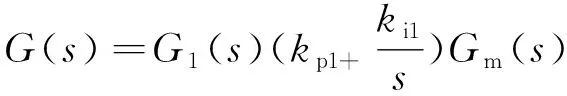
(4)

系统共存在6个极点和4个零点，为研究系统参数影响度和稳定性，将传递函数化为标准形式

( 5)

绘制根轨迹，见图5。根据图5可得，G1(s)对应一个远离坐标原点的负实轴极点，Gm(s)则对应共轭复数根零点和极点，将其放大，如图6所示，根轨迹起始于开环极点，终止于开环零点。

图5 系统根轨迹

传动系统存在一对欠阻尼的共轭复数极点，，其振动形式是衰减的正弦振荡，频率为ωp。

将图5中实轴附近根轨迹放大，如图7所示。

图7 系统部分根轨迹

G1(s)带来的两个极点中，一个远离虚轴(图5)，另一个与零点-ki2/kp2重合，因此G1(s)中的两个极点在之后的分析中忽略不计。而速度调节器存在一个0极点和一个零点为(-ki1/kp1,0)，速度PI带来的开环极点0，以该零点为终点形成根轨迹，而G1(s)带来的0极点与图5中远离虚轴的负实数零点重合然后朝着实轴正、负方向移动。

由此可得，该系统的稳定性主要与机械环节所对应的3个极点和速度调节器对应的1个极点的根轨迹相关。

根据对Kg影响参数的分析，系统稳定性主要跟速度PI参数kp1、电流PI参数kp2、电机转动惯量Jm相关，而在实际列车中，电机转动惯量是固定的，负载转动惯量Jl会发生变化，因此本文主要观察kp1、kp2、Jl对系统稳定性的影响情况，见图8。随着速度环kp1(图8中)(由8依次递减至5)或电流环kp2(图9中)的减小(由100依次递减至70)，ωp不变，共轭极点向右平移，其主导地位更强，系统稳定裕度变低，根据参数的变化规律，相比kp2而言，kp1对系统稳定性的影响作用更大。

同理，由图10可得，随着Jl的减小，ωp变大，共轭极点靠近虚轴，稳定裕度越低。

图8 kp1变化零极点影响图

图9 kp2变化零极点影响图

图10 Jl变化零极点影响图

1.3 机电耦合仿真分析

本文在MATLAB的Simulink上搭建了牵引传动系统模型，该模型采用CRH2A动车组实际参数模拟列车运行状况，其中逆变器直流侧输入电压额定值为3 000 V，电流额定值为432 A，异步电机控制选用矢量控制方式。

设置负载转矩为500 N·m，系统转速指令100 km/h，0～4 s加速过程相当于转速指令阶跃过程，当速度稳定后，第6 s设置负载转矩阶跃从500 N·m减小到100 N·m。

图11 电机转速及转矩仿真波形

转速和转矩都出现了明显的弱阻尼谐振现象，见图11，谐振频率为21.3 Hz，振动时间约为0.5 s。

电机和负载的转速偏差是反映机电耦合振动的重要参数。研究扭转振动现象的同时，对比不同电气参数kp1、kp2和机械参数Jl对扭转振动的影响如图12、图13所示。

图12 电机-负载转速差

由图12(a)可得，速度环kp1值减小25%，系统振动加剧，持续时间变长。图12(b)中，电流环调节参数kp2减小的影响较小，但其仍会使稳定性变差。

图13 不同负载转动惯量Jl时转速差对比

设置Jl减小25%，振动持续时间和转速差振幅均会增大，稳定性变差；而结合1.1节分析同样可得随着刚度K的减小，振动更严重。

综上，当系统存在不稳定因素时，会造成机械系统电机-负载转速差、转角差、转速转矩振动等现象，在电气控制系统中体现为速度调节器输出振荡、输出电流振荡等，影响扭转振动强弱的电气参数主要是速度控制器参数kp1，机械参数Jl对扭转振动也有一定的影响。

2 牵引传动系统扭转-弯曲耦合振动分析

第1节将机械环节简化成电机-负载双惯量模型，对传动系统稳定性和参数影响度进行了分析。在实测过程中，各个装置横向、纵向和垂向振动的测量反映的是系统的弯曲振动特性。因此本节进一步建立了考虑齿轮箱弹性悬挂的扭转-弯曲振动模型，将系统的电气振荡转化为机械振动，通过理论建模和机电耦合仿真对联轴节、齿轮箱和车轮各个装置的振动进行分析，同时验证电气参数对振动的影响作用。

2.1 扭转-弯曲耦合振动模型

高速列车驱动装置主要包括电机、联轴节、齿轮箱、车轴、轮对以及悬挂装置等部分，如图14所示[18]。

图14 转向架驱动装置结构划分

以CRH2A型车架悬式牵引传动系统结构为例，通过合理的简化，可将图14所示的结构等效为如图16所示[20]的模型。图16中各部分参数的含义见表1。

图15 齿轮箱截面示意图

图16 考虑扭转-弯曲耦合振动模型

参数含义J'1电机转子+电机半轴转动惯量J'2电机半轴+联轴节+主动齿轮半轴转动惯量J'3主动齿轮半轴+车轴半轴+齿轮箱等效转动惯量J'4车轴半轴+轮等效到主动侧转动惯量K'1电机轴扭转刚度K'2主动齿轮轴扭转刚度K'3齿轮箱支撑刚度

设θ1、θ2、θ3、θ4和θ5分别为电机转子、联轴节、小齿轮、齿轮箱以及车轮和大齿轮转动的角度，齿轮传动比为n，则可用大齿轮和齿轮箱的角速度表示小齿轮的角速度波动情况，即

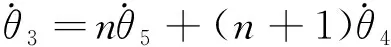
(6)

选取各部位的转动角度为状态变量，系统状态方程表达式为

(7)

将式(6)代入式(7)可得扭转-弯曲振动模型，然后将该机械模型加入到图4所示的传动系统电机控制模型中，可得系统幅频特性如图17所示。计算耦合振动的固有频率，其频率值见表2。

图17 扭转-弯曲振动模型波特图

编号频率/(rad·s-1)峰值/dB频率/Hzω1bend34.502.125.49ω2bend152.0016.2024.20ω3bend329.00-20.6052.39

由结果可发现，加入扭转-弯曲振动模型后，速度控制系统存在3个谐振频率点，其中以ω2bend=24.2 Hz对应的谐振峰值最高，与双惯量系统中谐振频率21.3 Hz接近，ω1bend次之，ω3bend=52.39 Hz对应的谐振峰值为负，该频率的振动分量很弱。

2.2 机电耦合仿真分析

设置仿真条件与2.1节相同，在速度达到稳定时刻(约14 s时)，电机转矩出现频率约为24 Hz的脉动，如图18所示。

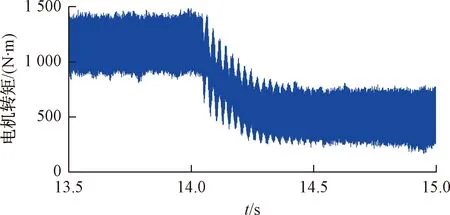
图18 电机转矩波形

当速度达到稳定(20 s时)，令负载转矩发生阶跃，同时调节kp1，观察驱动装置各个组成装置的角加速度见图19。

由图19振动结果可得，轴系各个装置在外界产生扰动等不稳定情况下时，都产生了不同程度的振动。其中振动最强烈的是齿轮箱，次之是车轮，然后是联轴节。3者的角加速度振动幅值分别为25、12、3 rad/s2。

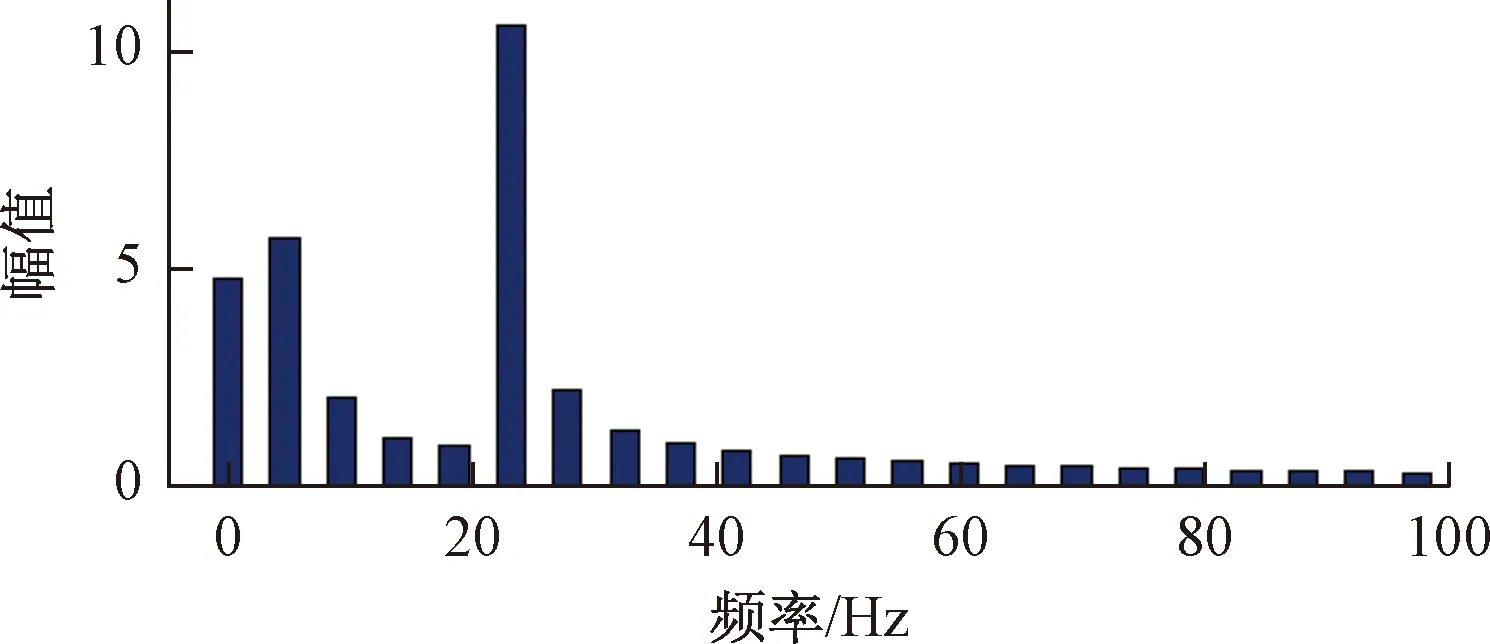
图20 角加速度FFT分析

由图20可知，振动频谱中主要包含两个谐振频率，其中约24 Hz的频率分量最高，约5 Hz的频率分量次之，与表2中的结果一致。

同时，由图19可得，设置kp1减小25%时，各个部件的振动都有所加剧，联轴节振动角加速度幅值增加了约4 rad/s2，齿轮箱约2.5 rad/s2，车轮约2 rad/s2，稳定性变差。

调节电流环参数kp2的大小，但其对振动影响非常微弱，以齿轮箱为例，设置kp2减小25%时的角加速度对比结果如图21所示。

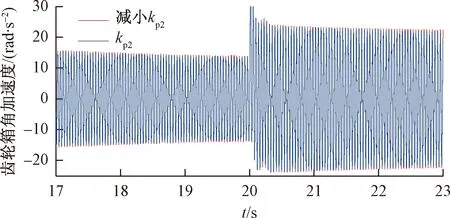
图21 调节kp2时齿轮箱角加速度对比

3 实验结果及分析

在实验室设计搭建了1.1 kW小功率机电耦合振动实验平台，主电路图如图22所示，两台逆变器分别驱动两台异步电机。两电机中间加入齿轮传动装置，并在齿轮传动装置的垂向加装振动加速度传感器，用于测量其振动状态。在齿轮箱和台架中加装了10 mm厚的弹性材料(橡胶)。

图22 实验平台搭建框图

由于齿轮箱的传动比为4∶3，在牵引侧选用4极电机，负载侧采用6极电机，电机和齿轮箱的连接采用梅花形联轴节，见图23。

图23 实验装置图

设置转速指令在第30 s时由200 rad/min速阶跃至800 rad/min，负载转矩为5 N·m，振动加速度波形如图24所示，振动加速度有明显增加，对其进行短时傅里叶分析，振动频谱分析如图25所示。

图24 振动加速度波形

图25 齿轮箱振动频谱分析

由图25可得，系统存在一个不随速度变化的固有频率，即为装置谐振频率，约为180 Hz。提取180 Hz附近的频谱结果，观察该频率对应的幅值变化，如图26所示。

图26 180 Hz附近振动频谱(kp1=0.02)

由图26可得，当系统产生阶跃时，谐振频率的振动明显加剧，振动峰值增加至了0.019 1g，在第35 s到50 s时，振动峰值由前30 s的0.006 8g增加至了0.015 9g，增加了1.34倍，之后振动加速度缓慢减弱，保持在0.012 3g左右，现象与理论仿真分析一致。

图27 调节kp1时180 Hz附近振动频谱

调节速度环参数kp1的大小，各振动峰值对比结果如图27和表3所示。

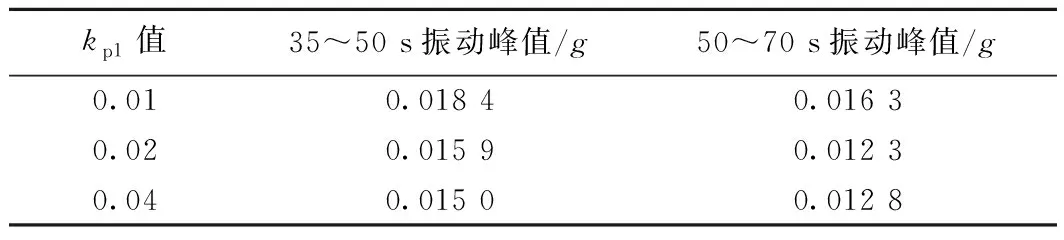
表3 不同参数振动幅值对比

如图27(a)所示，减小kp1=0.01时，在30 s时的振动峰值，约为0.02g，相比kp1=0.02时的振动峰值增加了15.72%，而50～70 s时增加了32.52%；而kp1增加至0.04，振动有明显的衰弱，振动峰值较kp1=0.02时衰减了5.66%，之后大部分时间均低于0.01g。由此可得，kp1减小则齿轮箱振动越剧烈，振动衰减越缓慢。