人脸追踪机械臂的运动学研究
2019-11-08李丽宏
崔 晨,李丽宏
(太原理工大学 电气与动力工程学院, 太原 030600)
人机协作是工业机器人领域最热门的研究方向之一,协作机器人已经成为一个新的研究热点[1]。在协作机器人领域,鲜有人将人脸追踪和机械臂结合。因此本研究设计了人脸追踪机械臂,六轴机械臂由六个高集成度科尔摩根关节模组构成,末端连接显示屏和Kinect视觉检测装置,用于将显示屏实时跟随人脸,协助人的日常工作,其原理如图1所示。
人脸追踪机械臂的工作流程如下(见图2),首先是通过设计的上位机界面开启Kinect视觉传感器并使能机械臂,Kinect将实时捕捉的人脸位姿返回机械臂控制模块。同时控制模块通过关节模组编码器采集电机当前位置。两者在控制模块中经过运动学解析得出各关节转动量,控制机械臂运动到指定位姿。

图1 人脸追踪机械臂仿真原理示意图
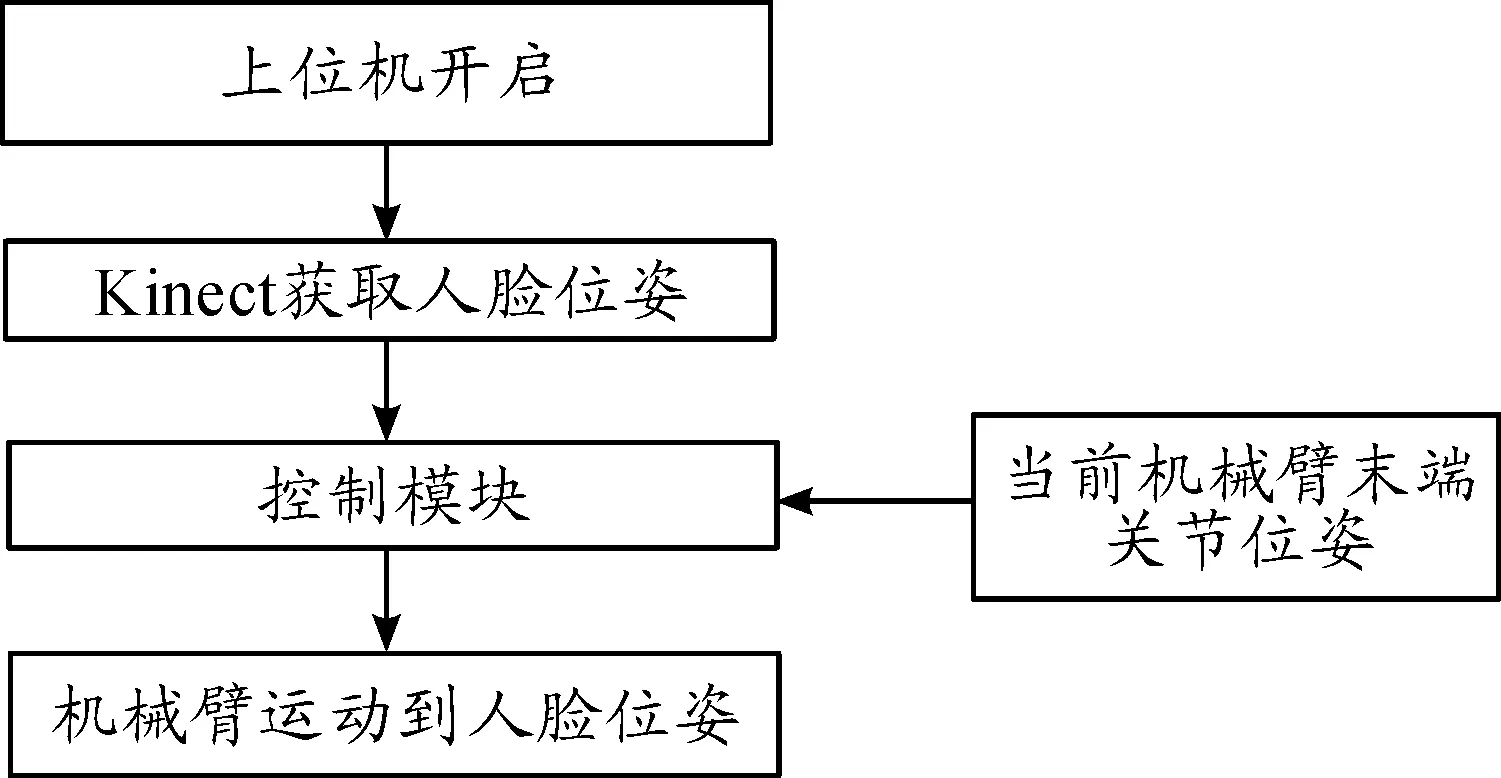
图2 人脸追踪机械臂工作流程框图
而人脸追踪机械臂的控制主要是对其末端执行器的位置和姿态进行控制,以使机械臂完成相应的动作。因此,对机械臂进行运动学分析是机械臂实现人脸追踪必不可少的一个环节。
当前已有不少学者对六自由机械臂运动学进行了分析研究,例如:姜宏超等[2]对符合Pieper准则[3]的六自由度模块化机械臂MT-ARM进行逆运动学分析;张化平等[4]针对MOTOMAN-MA1400安川弧焊工业机器人进行运动学分析,并运用Pro-E建立了机械臂运动仿真平台;王立权等[5]针对6R关节型机器人推导了代数逆解结果,并研究了逆解的漏根、增根和多根问题;莫毅[6]对六自由度工业机器人建立D-H模型,通过对机器人本体的标定测量,验证了D-H模型的正确性。
上述研究虽然都是针对六自由度的机械臂,但是机械臂机械结构均是末端三轴轴线相交于一点,符合Pieper法则之一,即3个相邻关节交于一点;而本文后三轴轴线不相交于一点,如图3,但是2、3、4轴轴线方向平行,如图4,同样满足Pieper法则,即3个相邻关节轴相互平行。虽然都是六自由度机械臂存在封闭解[7]的充分条件。但是因为现实中大多数机械臂符合前者相邻三轴交于一点的条件,相应的其运动学研究也很丰富。鲜有满足后者条件的机械臂,对应的其运动学研究较少。因此针对本机械臂,通过D-H法得到机械臂正解,而求逆解方法采用解析法[8],可以得到全部解。通过Matlab机器人工具箱检验正逆运动学,运用胶囊碰撞检测算法设定约束条件选取最优解。本机械臂设定允许位置误差范围为10 mm,姿态角误差范围为0.02。

图3 机械臂后三轴轴线示意图
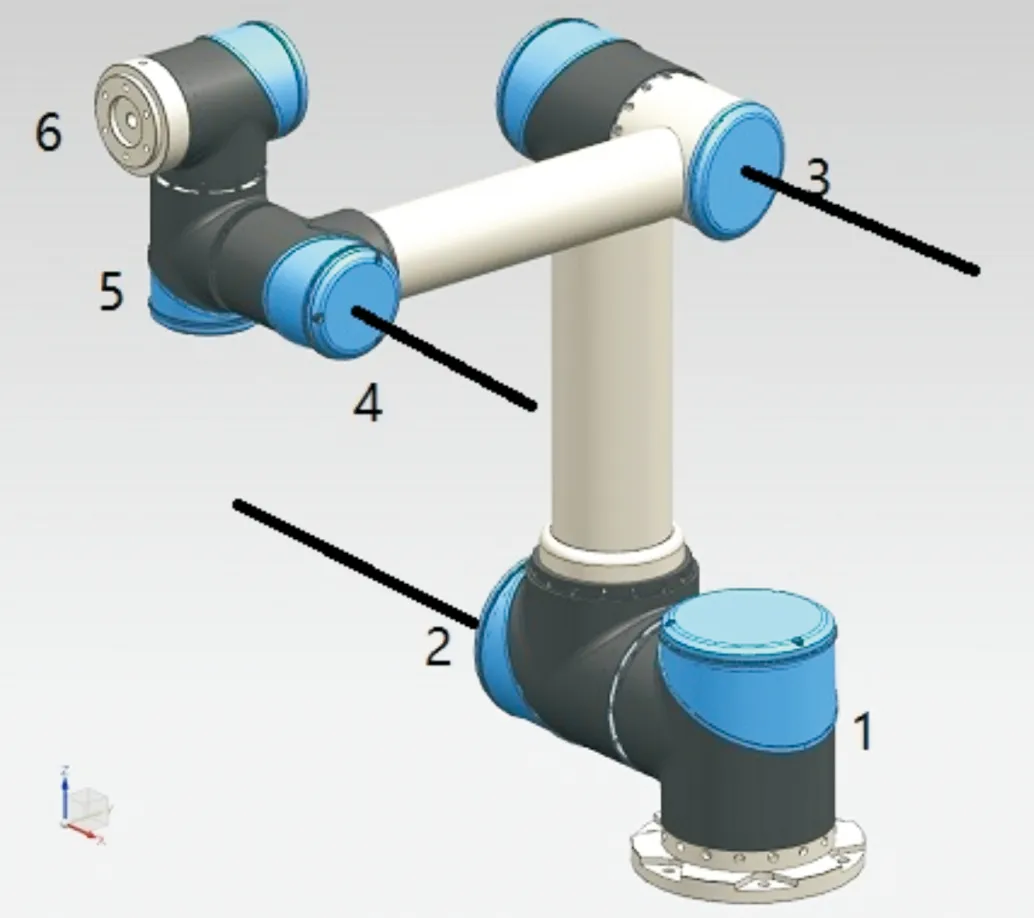
图4 六自由度协作机械臂机械结构设计模型示意图
1 六自由度机械臂的正运动学分析
机械臂机械结构仿照优傲公司UR系列,由六个科尔摩根RGM关节模组构成,六个关节均为转动关节。分别为基座关节1,大臂关节2,小臂关节3,手腕关节4、5、6,分别控制俯仰角、偏航角、滚动角[9]。
采用D-H法建立连杆坐标系,分别给六个关节建立一个参考坐标系,实现任意相邻两个坐标系间的转换,最后得出正运动学总变换矩阵。
如图5所示即为建立的六自由度协作机械臂的笛卡尔直角坐标系,表1为所建模型对应的参数值。

图5 六自由度协作机械臂D-H坐标系

(1)
将D-H参数代入式(1),得到相邻关节间的变换矩阵,最终得到足端坐标系相对于基座标的总变换矩阵为:

(2)
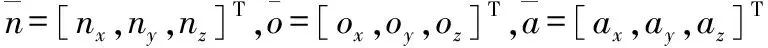
(3)
即式(3)为式(2)左上角元素构成的3维方阵。
2 六自由度机械臂的逆运动学分析
运动学逆解是已知末端位姿求解各关节角度,其解可能存在多重解,也可能无解。下面采用矩阵逆乘法[12]求解六自由度协作机械臂逆解。
2.1 首先求解θ1、θ5和θ6

(4)
由式(3)左右两边矩阵第三行元素相等得:
nxs1-nyc1=c6s5
(5)
oxs1-oyc1=-s5s6
(6)
axs1-ayc1=c5
(7)
pxs1-pyc1=70c5+155.3
(8)
由式(7)、式(8)得:
θ1=atan2(py-70ay,px-70ax)+
(9)
为使θ1有解,必须有(px-70ax)2+(py-70ay)2-155.32≥0,θ1有两个解。
由等式(4)、式(5)得:

(10)
因为θ1有两个解,所以θ5有4个解。
由式(7)、式(10)得:
(11)
当s5=0时,即θ5=nπ(n=0,1,2…),此时机构发生奇异,无法求出θ6。
当θ5≠0时,
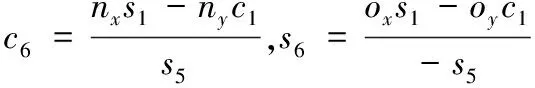
θ6=atan2(s6,c6)
(12)
将θ5代入式(12),θ6也有4个解。
式(1)等号两端矩阵的(1,3),(2,3)元素对应相等,可得:
-c234s5=axc1+ays1
-s234s5=az
联合求解可得:
(13)
2.2 求解θ2、θ3和θ4
(14)
令式(14)的(1,4),(2,4)元素对应相等,得:
-350c23-400c2=m1
(15)
-350s23-400s2=m2
(16)
其中,
m1=102.3s6(nxc1+nys1)-70axc1+pxc1-
70ays1+pys1+102.3c6(oxc1+oys1)
m2=pz-70az+102.3ozc6(oxc1+oys1)
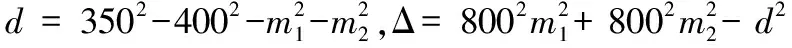
(17)
θ23=atan2(400s2+m2,400c2+m1)
(18)
进而求得:
θ3=θ23-θ2
(19)
由式(13)、式(18)得:
θ4=θ234-θ23
(20)
因为m1、m2分别有4个值,所以θ2有8个解,继而θ3和θ4也分别有8个解。
综上所述,本研究所描述的六自由度协作机械臂最终可以得到8组逆解。
3 仿真验证
为了验证六自由度协作机械臂的正逆运动学的正确性,首先应用蒙特卡洛法分析了机械臂工作空间,在可达工作空间范围内随机选取姿态点,结合机械臂实例并利用Matlab中的机器人工具箱[13]进行验证。下文选取一组工作空间内的位姿值阐述运动学正逆解相互验证分析[14]的具体方法,统计出8组逆解计算精度,并进行理论分析和解释。
3.1 六自由度机械臂工作空间分析
使用蒙特卡洛法[15]计算机械臂工作空间,基于运动学模型,通过计算机伪随机算法,在各关节物理约束下生成关节变量,代入正解矩阵计算机械臂末端执行器的位置。
由图6所示的三维工作空间示意图得出,六自由度协作机械臂在X轴方向为:-882 mm到882 mm,Y轴方向:-882 mm到882 mm,Z轴方向:-363 mm到967 mm。
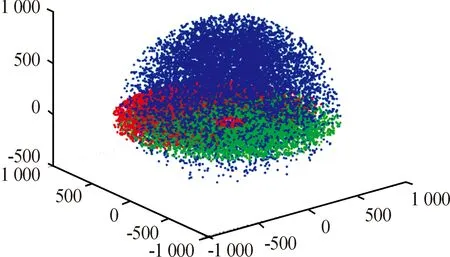
图6 六自由度协作机械臂三维工作空间示意图
3.2 六自由度协作机械臂正逆解验证
选取的位姿值W=[-387.300 0、-204.600 0、487.300 0、-54°、30°、125°],位置值px、py、pz分别为:-387.300 0、-204.600 0、487.300 0和姿态角R、P、Y分别为:-54°、30°、125°。根据前文所述的逆解计算方法,运用Matlab编写矩阵的逆解程序,将W代入编写的Matlab逆解函数中得到8组逆解[16],如表2。
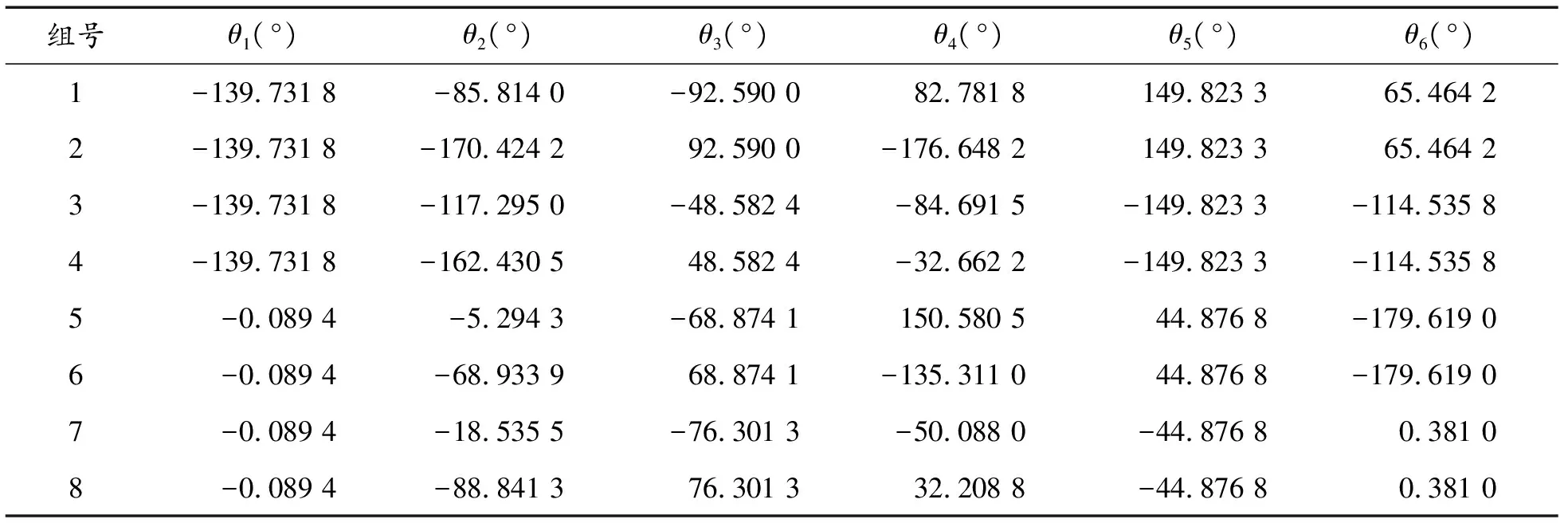
表2 8组逆解
将所得的8组逆解分别输入机械臂控制器中,机械臂运行的最终状态如图7所示。

图7 六自由度协作机械臂实际运行的最终状态
将8组逆解依次代入正解齐次变换矩阵[17]式(2)得到8组正解矩阵。其中,T1为第一组逆解代入得到的正解矩阵。
(21)
随后采用机器人工具箱Robotics Toolbox[17]中提供的函数对六自由度机器人建模,用表二中8组逆解中的第一组代入仿真程序得到如图8所示的仿真结果,并得到仿真正解矩阵式(22)。
(22)
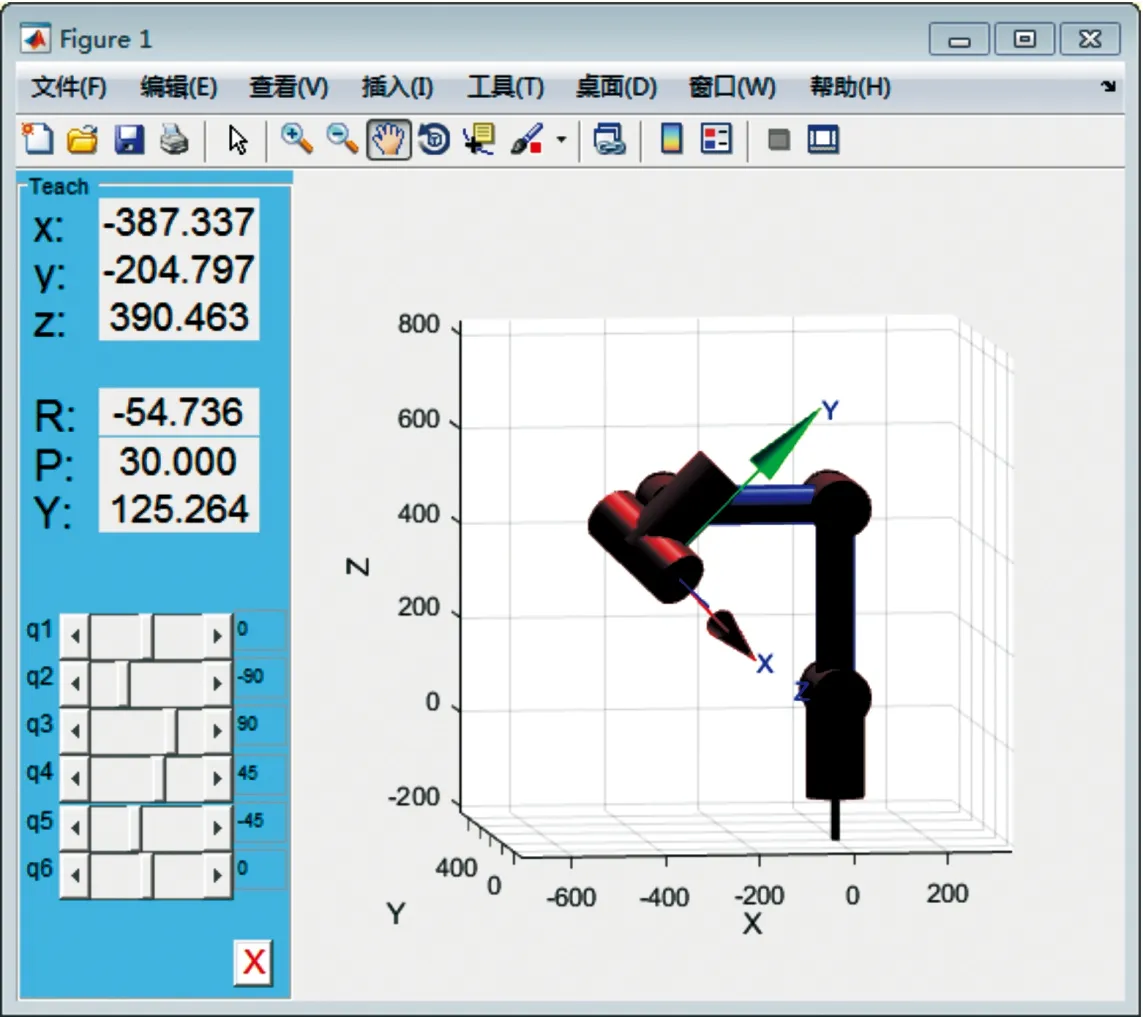
图8 六自由度协作机械臂Matlab仿真结果
对比Matlab机器人工具箱仿真得出的正解矩阵(22)与前文正运动学建模得出的正解矩阵(21)T1。计算两个矩阵之间的相对误差,其余7组对比方法相同。
误差分析分为姿态误差和位置误差,姿态误差,由式(3)所示的姿态矩阵,即矩阵的左上角三维矩阵求得。位置误差则有矩阵最后一列的位置值求得。
(23)
(24)
根据式(23)和式(24)可得全部8组误差,如表3所示。

表3 误差 ‰
由表3可得姿态误差在2‰与3‰之间,位置误差则保持在万分位上,完全能够满足人脸追踪机械臂得定位要求。
在机械臂可达工作空间范围内另外选取5组位姿值,重复同样的实验步骤,得到的姿态误差和位置精度与表3相符。
综上,仿真结果均和正解矩阵得出的结果一致,证明运动学正解模型正确。
4 最优解的选取
针对六自由度协作机械臂最优解的选取经过三轮筛选,以表2的8组逆解为例进行说明。
第一轮筛选:基于机械臂物理关节约束条件,防止机械臂在运行过程中关节轴与连接杆间自身产生物理碰撞,根据机械臂机械结构得出本文六自由度协作机械臂物理关节约束如下:
-180°<θ1<180°, -180°<θ2<0
-130°<θ3<130°, -180°<θ4<180°
-160°<θ5<160°, -180°<θ6<180°
第二轮筛选:如图7所示,机械臂安装在工作台上,为防止机械臂运行中触碰工作台,根基几何位形,大臂和小臂的位姿形态应符合:两者的垂直距离之和必须高于工作桌面。
因此θ2和θ3需满足如下关系式:a3sin(-θ2-θ3)+a2sin(-θ2)<0。
经过前二轮筛选后,表2前四组解均满足条件。
第三轮筛选:基于第二轮筛选,计算符合物理约束的每组逆解的关节转角绝对值总和,计算结果越小,表示转动角度和越小,转动消耗的能量越小,第一组解计算结果最小,因此第一组解选为最优解。
5 结论
针对本研究的人脸追踪机械臂,根据相邻三个关节轴轴线方向平行存在封闭解这一充分条件,运用D-H法建立机械臂的关节坐标系,求得机械臂的运动学正解,采用解析法,通过矩阵逆乘求解各关节角度值。
运用蒙特卡洛法分析了机械臂工作空间,选取工作空间的位姿值,通过Matlab中的机器人工具箱,验证了机械臂运动学正逆解的正确性,从而得到了该机械结构类型的六轴机械臂的一般性运动学逆解方法。
