聚碳酸酯在高应变率下的动态力学性能研究

李艳辉,高玉波

(中北大学 理学院， 太原 030051)

聚碳酸酯属于典型的玻璃态聚合物，具有良好的物理力学性能，如密度低、透明度高、抗冲击性能强、生产成本低等特点，常用于特殊军事和民用结构的防护，例如战斗机座舱盖、高铁的挡风玻璃、建筑物的防护幕墙等。作为航空防护结构，聚碳酸酯通常能承受一定的高速弹丸、冰雹、鸟撞等冲击。因此，聚碳酸酯材料在高应变率条件下的动态力学性能研究至关重要。

近年来，不同应变率条件下聚碳酸酯的动态力学行为研究受到了广泛关注。Wang等[1]开展了10-4～103s-1应变率范围内聚碳酸酯的动态力学响应特性研究，考虑α相和β相之间相变的影响，提出了一个绝热模型预测聚碳酸酯的动态力学性能表现。Dar等[2]通过单轴拉伸测试研究了注塑成型的航空标准光学聚碳酸酯的失效行为。Siviour[3]进行了聚碳酸酯的动态压缩应力应变性能研究，实验表明材料的屈服强度和应变率之间属于双线性相关。Senden和Safari等[4-5]对于聚碳酸酯材料的动态力学性能研究进行了详细总结。在极高应变率条件下，Carter,Mori和Millett等[6-8]设计了平板撞击实验确定了聚碳酸酯在不同形式下的Hugoniot曲线。然而，聚碳酸酯不同应变率下的压缩和拉伸载荷作用下将呈现不同的力学性能，而相关研究尚缺少详细描述。另外，对于一维冲击波加载下材料的状态方程参数仍存在较大分歧。

因此，本文针对聚碳酸酯材料不同应变率范围内的动态拉伸/压缩力学性能以及状态方程展开了详细研究。一维应力波加载由改进的分离式霍普金森压杆装置完成，并采用二维数字散斑相关技术研究了材料的动态变形。在极高应变率下，设计了一级轻气炮装置完成了聚碳酸酯材料状态方程的测试，设计装置包含锰铜计测试系统、PVDF测试系统和粒子速度测试系统构成。

1 实验设计

1.1 动态拉伸、压缩实验

图1是动态压缩试验的实验装置示意图。铝合金压杆的密度ρ0=2.7 g/cm3，弹性模量E=70 GPa，直径d=12.7 mm。入射杆和透射杆的长度均为1 200 mm。撞击杆的尺寸为Φ12.7×300 mm。对于拉伸试验，撞击杆的尺寸：内径18 mm，外径30 mm，长度300 mm。

图1 动态压缩测试系统示意图

本文采用的聚碳酸酯密度为1.2 g/cm3。动态压缩试验所用的试样尺寸为Φ8 mm×6 mm的圆柱。对于动态拉伸试验，试样和拉杆之间采用螺纹进行连接。拉伸试样的直径为 4 mm，长度为9 mm。为了验证动态压缩和拉伸的实验数据，采用二维数字散斑技术(2D-DIC)测量试验中试样的动态变形过程，其试样散斑如图2所示。散斑大小用喷漆雾化来控制。高速相机的帧率在压缩和拉伸试验中分别是160 000帧和80 000帧。

图2 试样散斑示意图

1.2 平板撞击实验

平板撞击实验采用57 mm口径的一级轻气炮装置，飞片选用LY12铝合金实现非对称撞击，尺寸为 Φ50 mm×4 mm。图3为实验装置示意图。聚碳酸酯试样厚度为4.3 mm，包括一个直径Φ76 mm的支撑板和两个直径Φ50 mm的测试板，敏感元件安装于板之间，如图4所示。

图3 平板撞击实验装置示意图

图4 平板撞击试验试样的安装示意图

平板撞击实验包括3个测试子系统：锰铜计测试系统，PVDF测试系统和电磁粒子速度测试系统。

锰铜计测试系统，选用H型片状结构(电阻为2 Ω)，如图5(a)所示，其应用范围比较宽0.1～50 GPa。示波器前安装一个阻值为50 Ω的并联电阻以防止同轴电缆在终端的干扰。PVDF测试系统采用电流模式，电路图如图5(b)所示。其中，R为测试电阻(120 Ω)，Rm为匹配电阻(50 Ω)，U0(t)和i(t)分别为测试电阻的电压降和电流降。电磁粒子速度测试系统示意图如图5(c)所示，将敏感元件安装于永磁体装置的中央区域，此处磁感应强度B为2 690 Gs。根据法拉第电磁感应定律，导体切割磁感线运动会产生感应电动势：

E=B·l·u

(1)

其中，E是关于单变量u的函数，由此可以推算物质内部的粒子速度。

图5 三个测试子系统的电路示意图

2 动态压缩力学性能

(2)

(3)

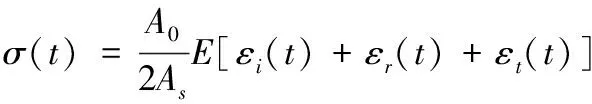
(4)

其中：L和As为试样的初始长度和横截面积，C0、A0、E分别为压杆声速、横截面积和弹性模量。

加载应变率通过改变轻气炮高压气室中氮气压力来控制。图6为实验典型的入射、反射和透射信号，如图6所示，试样的加载满足应力平衡。

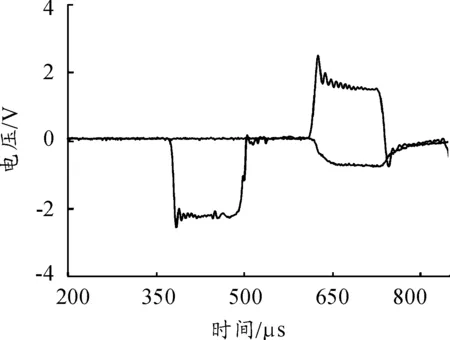
图6 动态压缩加载下典型信号

图7是动态压缩试验中不同应变率下的真应力-应变曲线。由于强化效应代替了动态变形滞后现象，当应力达到屈服点时，材料的应力应变曲线并没有出现应力软化。随着应变率的增加，动态抗压强度也不断增加，而增量逐渐减小。聚碳酸酯的弹性模量在不同的应变率下有着相似的现象。因此，聚碳酸酯是典型的应变率敏感材料，在高应变率加载条件下会产生应变强化效应。

图7 动态压缩加载下随应变率下的真应力-应变曲线

如图8为应变率为1 931 s-1下由霍普金森杆试验和二维数字散斑相关技术得到的试样应变历程曲线。结果表明：动态压缩下应变片处理结果与二维数字散斑相关技术应变历程吻合较好，进一步验证了本实验测试的有效性。

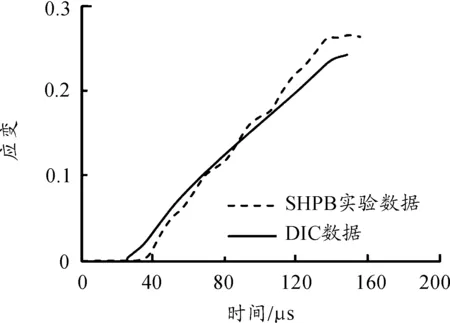
图8 试样应变历程曲线(1 931 s-1)

3 动态拉伸力学性能

由图9典型入射波和透射波信号和应变率历程曲线可知，对试样的动态测试满足应力平衡状态和常应变率加载条件。

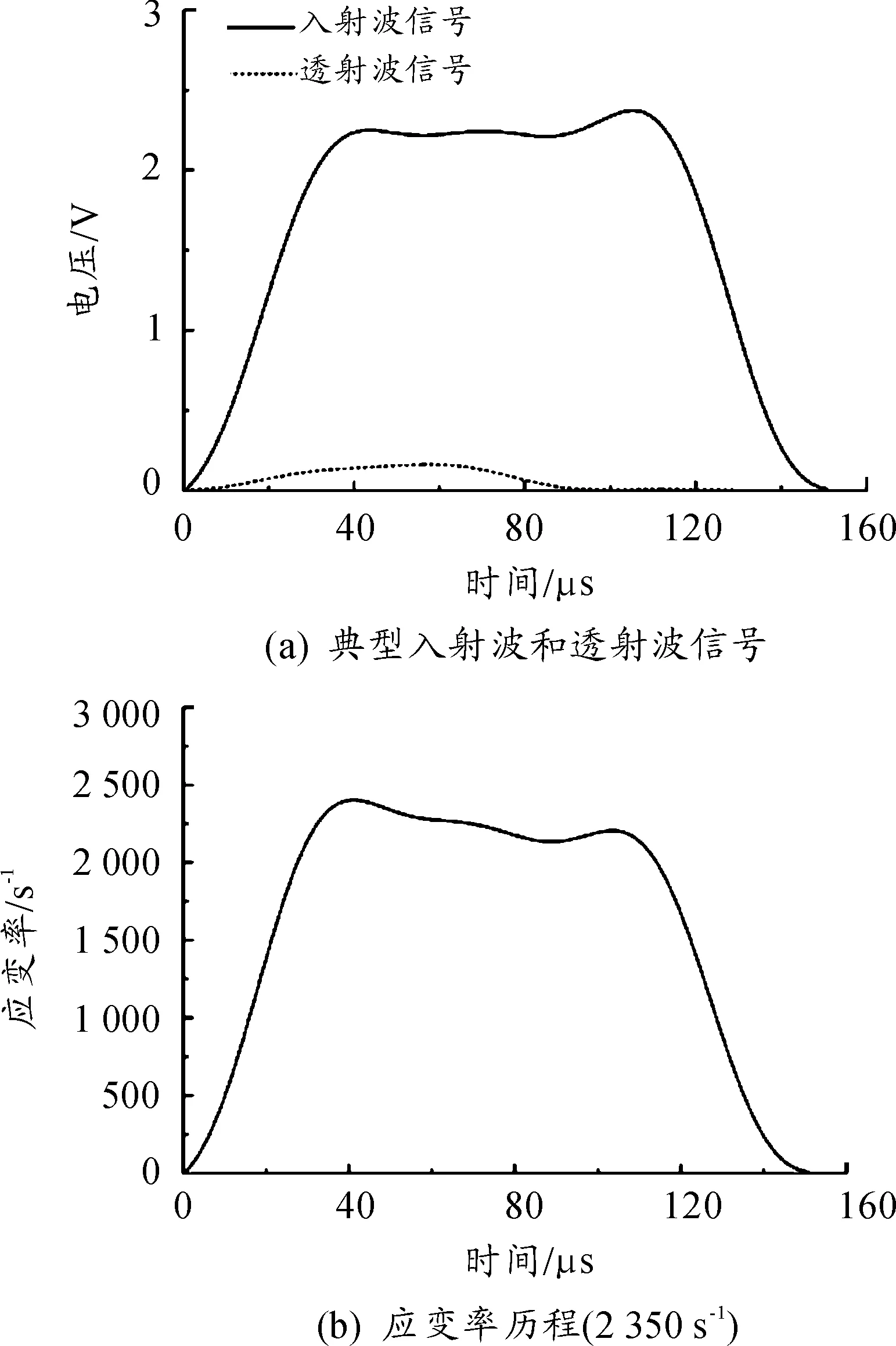
图9 动态拉伸加载下典型信号和应变率历程曲线

如图10所示，聚碳酸酯材料动态拉伸加载下应力-应变曲线表现出明显的非线弹性特征，且动态拉伸强度随着应变率的增加而增加，属于典型的应变率敏感性材料。在拉伸试验中，聚碳酸酯材料的应变率敏感性与压缩试验相比表现出相似的力学特性。

图10 不同应变率下的真应力应变曲线

图11是在应变率2 350 s-1下霍普金森杆和二维数字散斑相关技术得到的聚碳酸酯的应变历程。由图可知，通过霍普金森杆试验得到的应变与通过二维数字散斑相关技术得到的试验数据相吻合，进一步验证了本实验测试的有效性。

图11 实验的应变历程曲线(2 350 s-1)

4 高压状态方程

冲击波波阵面前后满足质量守恒，动量守恒和能量守恒：

ρ0(D-u0)=ρ1(D-u1)

(5)

P1-P0=ρ0(D-u0)(u1-u0)

(6)

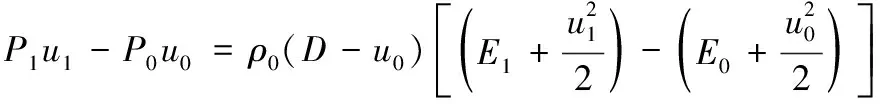
(7)

其中：D和u为冲击波速度和粒子速度，E为内能，P为压力，ρ为密度。初始条件下，P0、E0和u0近似为0，于是有，

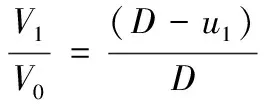
(8)

(9)

(10)

含有5个未知量，一般D和u两个变量需要通过实验的方法来获取。

在一定的压力范围内，聚碳酸酯材料的冲击波波速和质点速度呈线性关系，

D=C0+λu1

(11)

其中，C0和λ是常数。

冲击波速度由一次实验中锰铜计测试系统、PVDF测试系统和电磁粒子速度测试系统计算结果平均得到；质点速度由电磁粒子速度计直接获取，实验结果见表1。针对传统材料状态方程测试中单一敏感元件的测试手段，本文的方法可有效降低测试结果的误差。

表1 平板撞击实验结果

聚碳酸酯的D-u形式Hugoniot曲线通过最小二乘法拟合得到：D=2.39+1.55u。图12所示是冲击速度和质点速度的关系以及和前人数据的比较。

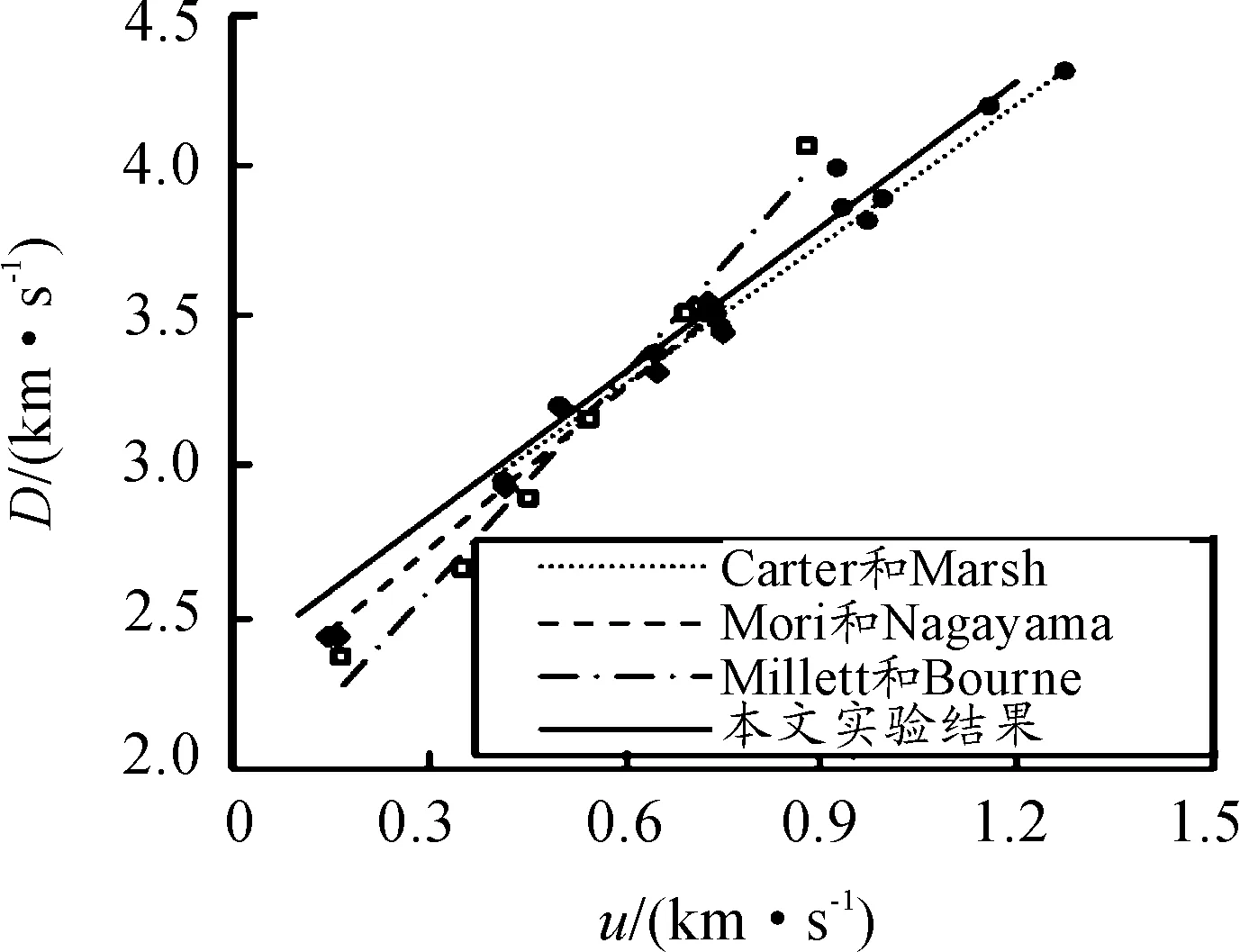
图12 平板撞击下聚碳酸酯材的冲击波速度和粒子速度

其中，Carter和Marsh获得粒子速度在0.4～2.6 km/s之间D-u关系式：D=2.33+1.57u。随后，Resseguier和Deleignies，Mori和Nagayama也都得到了相似的结果。分别是：D=2.20+1.53u和D=2.18+1.82u。Millett和Bourne得到的试验结果是D=2.87+2.4u。与前人数据相比较，本文的研究数据更接近于Carter和Marsh的结果。

5 结论

在动态压缩和拉伸实验中，聚碳酸酯的动态屈服应力表现出了明显的应变率效应。改进的霍普金森杆实验得到的聚碳酸酯材料的应变与二位数字散斑相关技术得到的结果具有很好的一致性，验证了实验的有效性。通过平板撞击试验设计获得了材料极高压条件下D-u形式的Hugoniot曲线。经过最小二乘法拟合发现，与前人数据比较，研究结果更接近于Carter和Marsh的结果。