城市轨道交通车辆车门故障分析及检修策略优化

单晓涛

北京交通运输职业学院 北京 100096

从全世界各国城市化发展的实践看，城市轨道交通作为一种绿色交通出行方式，其速度快、运量大、准点率高等优势，使其在公共交通出行中占比不断提高。我国城市轨道交通行业已进入快速发展新时期，运营的总规模、客运总量、在建线路的长度、规划线路长度等均创历史新高。北京作为全国城市轨道交通发展最早、规模最大的城市，截至2018年，总里程达到了609公里，运营线路共有22条，覆盖北京市11个市辖区，车站370座，日平均总客运量最高在1 000万人次左右。这就对轨道交通的专业技术、装备制造、检测维修等提出了极高的要求。

为了保障城市轨道交通车辆运行的可靠性和安全性，在运行一定时间后，车辆必须返回车辆段或停车场进行维修或保养。城市轨道交通车辆的组成相对复杂，由机械系统、电气系统、列车网络控制系统等组成。故制订科学合理的检修计划对保障车辆的安全可靠运行极为重要。本文是建立在教育部交通运输行业指导委员会城市轨道运输类专业指导委员会重点项目“城市轨道交通车辆检修技术研究和人才培养方案制订”的基础上，对城市轨道交通车辆故障信息进行统计分析，并对车门的检修策略进行优化和改善，使车辆检修工作更加科学化、系统化、标准化，以提高城市轨道交通车辆(以下简称“城轨”)检修的经济效益和社会效益。

1 城轨车门系统故障分析

根据北京地区城市轨道交通运营公司车辆段的检修规程和故障统计数据，选取北京地铁某线路2018年1月至2019年1月间的故障，发现车门的故障率最高，达到了总故障率的一半以上，对车辆的整体可靠性和安全性造成了巨大的影响。同时，在教学过程中，车门维护和检修是车辆技术专业教学的重点，也是教育部全国技能大赛的竞赛项目，所以对车门结构讲解和故障的分析显得尤为重要。城市轨道交通车辆客室门系统的结构组成如图1所示，图中组件名称见表1。

图1 城市轨道交通车辆客室门系统

表1 城市轨道交通车辆客室门结构组件

根据北京某地铁线路对车门系统的故障统计和分析，将车门系统故障按其发生原因、类别进行整理，见表2。

表2 常见车门故障原因统计表

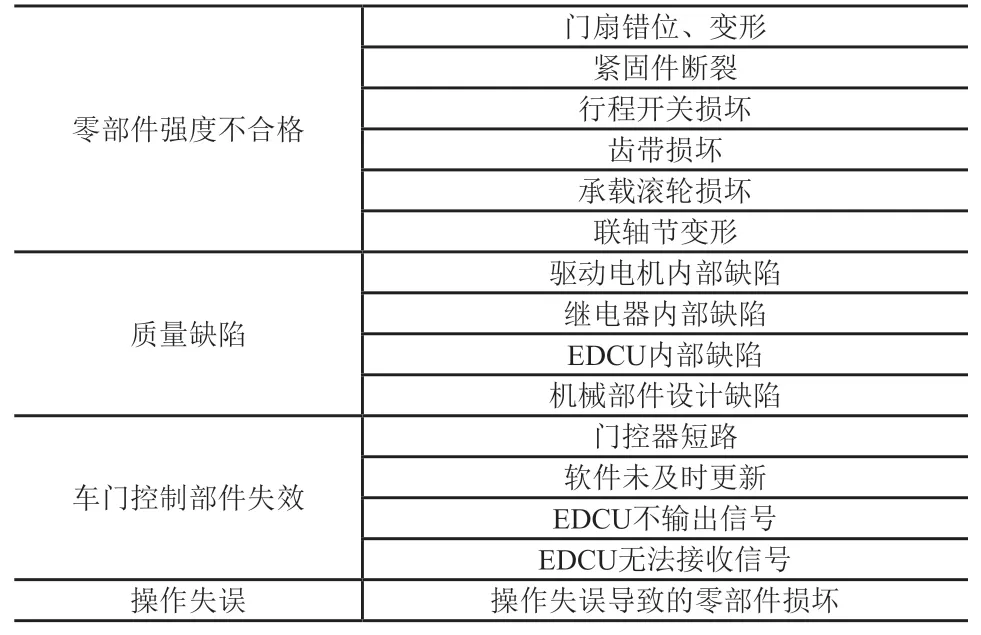
表2(续)

由表2可知，车门的故障主要分为机械系统故障和电气系统故障。

机械系统保障：内外紧急解锁装置松动，门扇变形，机架尺寸超限，外摆臂松动，车门滑道变形，车门V型间隙过大，行程开关损坏，隔离开关损坏等。根据现场维检修人员统计，紧固件松动在车门故障中占绝大多数。

电气系统故障：插线盘烧坏，插头松懈，码盘接线松动，端子排线束虚接，车门机架线束松动，门控电机故障等。

2 城轨车辆车门系统可靠性分析

了解车门的结构和故障类型后，其检修策略便成为学校教学、地铁企业维修作业的重点。目前车门维修均采取计划性预防维修[1]为主、均衡修[2]为辅的方式。在教学中如何引导学生根据故障数据，统计出故障规律，发现并提出更好的检修策略，提高学生学习的积极性和主动性，在提升工作兴趣的同时为企业生产做出贡献，显得极为重要。因此根据故障统计对车门进行可靠性[3]分析。

在对车门系统的故障进行统计时，选择60万～100万公里数据进行统计，因其正好在一个定修周期内，且在故障率较高的定修周期内，数据具有代表意义。在此期间，车门机械故障14 068次，电器故障2 756次，为了便于分析，本文只对车门机械部分的故障进行统计，见表3。

表3 车门机械故障统计表

根据车门的机械故障统计数据，以行驶里程为横坐标，分别绘制故障频数直方图、相对故障频数直方图、累积故障频数直方图和平均故障率直方图[4]。其中故障频数直方图是表示车门的故障数与行驶里程数之间的关系；相对故障频数直方图表示故障数的相对概率、累积故障频数直方图是故障随横坐标增长的一种累积曲线；平均故障率直方图表示行驶相应公里数时发生故障的概率。故障频数直方图如图2所示。

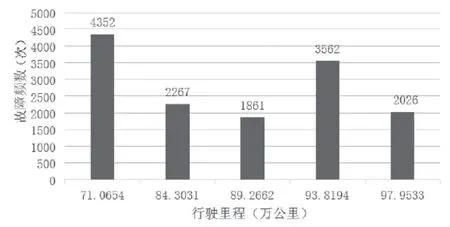
图2 车门故障频数直方图

相对故障频数直方图是在样本区间内，故障发生次数在不同行驶里程数时所占的比率，如图3所示。

图3 车门相对故障频数直方图

累积故障频数直方图表示故障数在行驶里程上的累积分布关系，如图4所示。

图4 车门累积故障频数直方图

平均故障率直方图表示行驶相应公里数时，设备发生故障的概率，如图5所示。

图5 车门平均故障率直方图

由上述四种直方图的形状可以初步判定样本的总体服从威布尔分布。

威布尔分布的参数变化可描述指数分布和正态分布，也称为“万能分布”[5]。结合随机截尾数据[6]的特点，本文主要采用威布尔分布作为寿命分布类型。下面介绍两个参数威布尔分布，包括概率密度函数式(1)和分布函数式(2)。

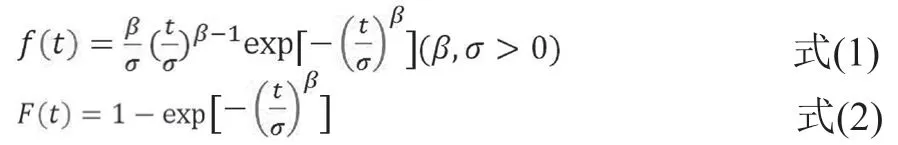
其中，t表示样本失效时间，β表示形状参数，σ表示尺度参数。

将式(2)两边取两次对数，整理可得：

ln{-ln[1-F(t)]}=βln(t)-βlnσ

为了表示方便，令y=ln{-ln[1-F(t)]}，x=ln(t)，a=-βlnσ，b=β，则上式可变换成：

工程上一般采用经验函数法进行分析，将样本数据带入经验函数公式中，样本量较少的可根据式(4)计算，如若样本量较大，可按式(5)计算。

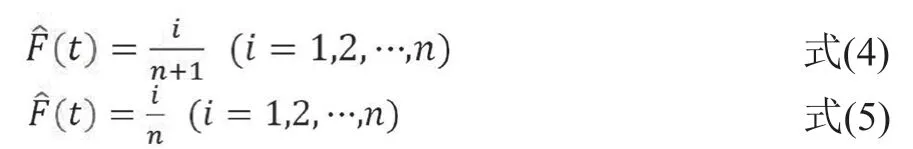
式(4)、式(5)中，n表示故障次数，经过数值计算，可得到分布函数数据点为后续深入分析做准备。

选取车门60万～100万公里运行数据作为研究对象，用经验函数法对其进行分析并进行参数的估计，以ln(t)为横坐标，ln{-ln[1-F(t)]}为纵坐标绘制直线，图6为威布尔坐标系下计算结果。

图6 车门威布尔线性模型

由图6计算得直线表达式为y=0.8637x-4.1488，进而计算出则该车门的威布尔分布函数为：

用K-S检验法对以上威布尔分布进行检验，检验统计量按式(7)进行：

式(7)中sup(*)为取值中最大值，Fn(t)为样本容量为n的经验分布函数，F(t)为理论分布函数。用最大偏差值Dn与临界值Dn,a相比较，若Dn〈Dn,a，则接受原假设，否则拒绝。

实际经验分布函数Fn(ti)为车门的累积故障概率值，结合理论分布函数式(6)，可计算出最大偏差值为0.214 6；以样本容量30，显著性水平α为0.01，查临界值表可得D(n,α)为0.29，因此有：

由式(8)可得，接受原假设，车门故障寿命分布服从威布尔分布。在教学过程中，可以根据故障数据，让学生分析车辆不同零部件的可靠性分布类型，从而对其检修策略提出优化方案。

3 城轨车辆车门检修策略优化

3.1 城轨车辆车门检修策略优化模型适用

检修策略优化[7]过程中引入数学模型，对于学生应用能力的拓展有极大好处。根据前面内容，城市轨道交通列车车门寿命模型服从威布尔分布，且车门故障率较高，容易发现，方便维修，不会造成停车损失，对整个车辆系统运行安全性影响较小，故可采用经济性要求下的维修周期优化模型[8]。车门在一个定修周期内进行了n次预防性维修，每次间隔时间为T，若在间隔期内发生故障则进行最小维修，在n+1次预防性维修时进行预防性更换；对车门的每次预防性维修均提高各零部件性能，但最小维修只能使系统的性能恢复到故障前，不改变零部件的可靠度和故障率；车门的预防性维修费用和最小维修费用均不大于更换费用，预防性维修、最小维修和更换时间忽略不计。

综上所述，城市轨道交通列车车门的检修策略符合经济性要求下的策略优化模型。为了描述方便，预防性维修费用、更换费用、最小维修费用分别用Cpm，Cr，Cm表示，维护后的改善程度通过η来衡量。

3.2 城轨车辆车门检修成本率函数的构造

成本率[9]的计算主要是费用与时间的比值。在车门一个定修周期内，维修成本包括一次更换费用，(n-1)次预防性维修费用和可能产生的最小维修费用，其中的难点是最小维修费用的计算。根据维修条件，最小维修费用产生在维修间隔期内，由于设备使用条件的不同和发生故障的复杂性，只能通过概率的方法进行描述。故若能得到在此间隔期内发生故障次数的期望值，即可完成维修成本率函数的构造。

要得到故障发生次数期望，不可避免地要引入系统故障率[10]的概念。系统的故障率也称故障的发生概率，是描述系统状态的重要参数。如果整个使用周期中故障率减少，则可说明其状态得到了改善。故障率是与时间关联的参数，随着使用时间的增长，故障率会发生相应的变化。为了得到维修成本，需要计算在预防性维修前后发生故障的期望值，公式如下：

其中，H(t)为未进行定期预防性维修时，间隔时间[0,t]内故障的期望值，λ(x)是初始的故障率，即未进行预防性维修时的故障率。

进行第n次定期预防性维修之前，故障率函数用λ(n-1)(t)表示，进行第n次定期预防性维修之后，故障率函数用λn(t)表示。期间预防性维修的时间间隔为T，则有：

当η=0时，λn(t)=λ(n-1)(t)，预防性维修前后，故障率不发生改变，此时预防性维修为最小维修。当η=1时，λn(t)=λ(n-1)(t-T)，说明预防性维修使得系统恢复到前一个定期维修时期的状态，即完全维修。由于η的取值为(0,1)，也就说明预防性维修前后，部件处于不完全维修状态，符合不完全维修理论要求。

经过一系列的定期预防性维修之后，若每次定期预防性维修都以程度η改善系统的性能，对于任意常数n≥0和t∈[0,T]，有如下公式：

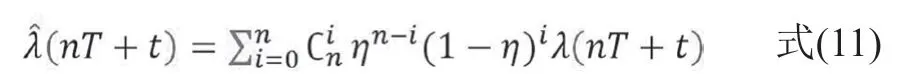
由式(10)、式(11)可知，不同维修次数对应的故障次数的期望值如式(12)：

设备的故障率函数表达式如式(14)：

由式(12)、式(13)、式(14)可得：

综上，可得到经济性要求下维修周期计算表达式：

其中，C(n,T)为成本率。

3.3 城轨车辆车门检修策略优化算例

在上文中，用车门故障数据采取图估法分析得出车门寿命为威布尔分布，形状参数β=0.863 7，尺度参数σ=121.938 9，其他参数如表4所示。

表4 经济性要求下模型相关参数

根据表4中数据，计算经济性要求下的维修周期，采用MatLab编程软件[11]实现，维修次数n从0～100取值，结果如图7所示。其中n=22，T=50.5天，维修费用率为C=46.4元/天。

图7 经济性要求下模型计算结果

可以看出，在城市轨道交通列车车门的检修过程中，在车门的一个定修周期内，进行22次维修，每次间隔50天，维修费用率最低，得到的经济效益最佳。最终建议的适用性还需根据现车试修验证。

4 结语

本文是城市轨道交通车辆技术专业学生综合能力的应用，通过从企业运营及维检修部门获得的数据，对城市轨道交通列车车门故障信息进行统计与分析；在不完全维修理论的基础上，结合设备寿命分布模型，建立基于改善因子的经济性要求下维修周期优化模型；通过对城市轨道交通列车车门的分析，验证了模型的可行性，并通过MatLab编程软件计算，给出最优的维修建议。研究要求学生在学习车辆检修理论知识的基础上，突出实际应用和知识拓展，强调创新能力，提升学习兴趣，为培养高素质、创新型技术技能人才提供了有效途径。