本期试卷参考答案
2019-11-07
编者的话:同学们在演练的过程中,如果需要更为详细的参考答案,请扫描右边的二维码,关注编辑部的官微“高中数学
解题反思”,不但能获悉详细参考答案,还可以另辟蹊径,开拓知识视野,学会解题反思!

函数应用综合演练A卷
一、选择题
1.提示:由题意知函数f(x)是增函数。根据函数的零点存在性定理及f(0)=-2<0,f(1)=e-2>0,可知函数f(x)在区间(0,1)上有且只有一个零点。应选B。
2.提示:易知的定义域为(0,+∞),且在定义域上单调递增。因为,所以f(1)·f(2)<0。由函数零点存在性定理知的零点所在的区间为(1,2)。应选B。
3.提示:因为第一次所取的区间是(-2,4),所以第二次所取的区间可能为(-2,1),(1,4),则 第 三 次 所 取 的 区 间 可 能 为应选D。
4.提示:因为f(x)的定义域为[0,+∞),所以易知函数f(x)在[0,+∞)上单调递减。因为所以函数的零点所在的区间为(1,2)。应选B。
5.提示:由表中数据可知,当单价为4元时销售量为400件,单价每增加1元,销售量就减少40件。设定价为x元/件时,日均销售利润为y元,则y=(x-3)·[400-(x-故当x=时,该商品的日均销售利润最大。应选C。
6.提示:因为函数在区间(1,2)上单调递增,又函数的一个零点在区间(1,2)内,所以f(1)·f(2)<0,可得(-a)(4-1-a)<0,即a(a-3)<0,解得0<a<3。应选C。
7.提 示:令f(x)+3x=0,则或解得x=0或x=-1,所以函数y=f(x)+3x的零点个数是2。应选C。
8.提示:根据题意可得l gA=l gA0+l g 10M=l g(A0·10M),所以A=A0·10M,则应选D。
9.提示:由题意可知函数f(x)在(-∞,-1)和(-1,+∞)上都是增函数,又-1+1=ln(-1+2)=0,所以f(x)是单调增函数。因为函数y=f(2-x2)-f(2x+k)只有一个零点,所以方程f(2-x2)=f(2x+k)只有一个根。因为f(x)是单调增函数,所以方程2-x2=2x+k只有一个解,即方程x2+2x+k-2=0只有一个解。由于Δ=4-4(k-2)=0,所以k=3。应选B。
10.提 示:由f(x)=0,可 得m=因为,所以解得-5≤x<10,x∈Z,可知x=-5,-4,-3,…,1,2,3,…,8,9,将它们分别代入m=验证可得符合条件的m取值为0,4,11,28,共4个。应选C。
11.提示:由函数图像可知f(±1)=0,1,g(±1)=-1,所以f[g(±2)]=f(1)=f(0)=0,f[g(0)]=f(0)=0,所 以f[g(x)]有7个零点,即m=7。又g[f(0)]=g(0)=0,g[f(±1)]=g(0)=0,所以g[f(x)]有3个零点,即n=3。故m+n=10。应选C。
12.提示:设售价在90元的基础上涨x元。因为这种商品每个涨价1元,其销售量就减少20个,所以若涨x元,则销售量减少20x,按90元一个能全部售出,则按(90+x)元售出时,能售出(400-20x)个,每个利润是90+x-80=10+x(元)。设总利润为y元,则y=(10+x)(400-20x)=-20x2+200x+4000,对称轴为x=5,所以当x=5时,y有最大值,其售价为95元。所以售价定为每个95元时,利润最大。应选C。
13.提示:由三视图可知,该容器的上部分为圆台,下部分是一个与上部分形状相同的倒放的圆台,所以水面高度随时间的变化为先慢后快再慢的情况。应选C。
14.提示:依题意并结合函数f(x)的图像可知代入化简解得应选C。
15.提示:由题意易知g(x)=2017x-为奇函数且在(-∞,+∞)上单调递增,所以g(1-2x)+3+g(x)+3>6,即g(x)>g(2x-1),可得x>2x-1,即x<1。故不等式f(1-2x)+f(x)>6的解集为(-∞,1)。应选A。
16.提示:因为当t∈[0,30]时,污染物数量的变化率是-10 ln2,所以-10 ln2=,所以p0=600 ln2。因为p(t)=所以p(60)=600 ln2×2-2=150 ln 2(m g/L)。应选C。
二、填空题
17.提示:令f(x)=0,当x≥λ时,可得x=4;当x<λ时,由x2-4x+3=0,可得x=1或x=3。若函数f(x)恰有2个零点,结合函数f(x)的图像(图略),可得1<λ≤3或λ>4。答案为(1,3]∪(4,+∞)。
18.提示:由题意可知f(x)在(0,+∞)上单调递减,f(3)<0,可知函数的零点x0∈(2,3),故k=2。
19.提示:由题意可得空闲率为,所以,其定义域为(0,m)。因为(0,m),k>0,所以当
20.提示:因为f(x)在(0,+∞)上单调递增,函数的零点在区间(1,2)内,所以f(1)·f(2)<0,代入化简解得2<m<5。故实数m∈(2,5)。
21.提示:将(1000,90)代入y=100 ea x,可得,则y与x的函数关系可近似表示为,当x=2000时,y=100(eln0.9)2=81。
22.提示:若模型为f(x)=2x+a,则f(1)=21+a=4,可得a=2,这时f(x)=2x+2,据此可得f(2)=6,f(3)=10,f(4)=18,与表中数据相差太大。若模型为f(x)=,则f(x)是减函数,与表中数据相差太大。若模型为f(x)=a x+b,由已知得解得所以故最适合的函数模型的序号为①。
23.提示:因为函数f(x)=4x-2x-a,x∈[-1,1]有零点,所以方程4x-2x-a=0在[-1,1]上有解,即方程a=4x-2x在[-1,1]上有解。方程a=4x-2x可变形为由x∈[-1,1],得2x∈所以故实数
24.提示:当x<1时,令ln(1-x)=0,解得x=0,可知f(x)在(-∞,1)上有1个零点,所以f(x)在[1,+∞)上也有1个零点。当x≥1时,令,得,所以实数a的取值范围是[1,+∞)。
25.提示:当t=0.5时,y=2,所以2=e0.5k,可得k=2 ln 2,这时y=e2tln2。故当t=5时,y=e10ln2=210=1024。
26.提示:设公司在A地销售该品牌的汽车x辆,则在B地销售该品牌的汽车(16-x)辆,所以获得利润y=4.1x-0.1x2+2(16因为x∈[0,16]且x∈N,所以当x=10或x=11时,总利润取得最大值为43万元。
27.提示:令y=f(2x2+1)+f(λ-x)=0,则f(2x2+1)=-f(λ-x)=f(x-λ)。因为f(x)是R上为单调函数,所以2x2+1=x-λ只有一个实根,即2x2-x+1+λ=0只有一个实根,则Δ=1-8(1+λ)=0,解得
三、解答题
28.提示:f(x)=x-a-x的零点x1是方程x=a-x的解,即是的解,g(x)=xlogax-1的零点x2是方程xlogax-1=0的解,即是的解,所以x,x是12y=ax和y=logax与的交点A,B的横坐标,可得0<x1<1,x2>1。因为y=ax与y=logax的图像关于y=x对称的图像也关于y=x对称,所以点A,B关于y=x对称。设点所以点A关于y=x的对称点与点B重合,可得即xx=1。所以x2113=5,即x1+4x2的取值范围是(5,+∞)。
29.提示:(1)f(2)=log33=1。
当x>1时,由f(x)=3f(2)=3,得x+1=27,即x=26;当x≤1时,由f(x)=3,得5-x=8,即x=-3。故方程f(x)=3f(2)的解集为{-3,26}。
(2)当x>1时,f(x)=log3(x+1)单调递增,且f(x)∈(log32,+∞)。
当x≤1时,f(x)=log2(5-x)单调递减,且f(x)∈[2,+∞)。
由g(x)=f(x)-a=0,得f(x)=a。
故当a∈(-∞,log32]时,g(x)的零点个数为0;当a∈(log32,2)时,g(x)的零点个数为1;当a∈[2,+∞)时,g(x)的零点个数为2。
30.提示:(1)由图像可设y1=k1x+29,y2=k2x,把点B(30,35),C(30,15)分别代入y1,y2,可得所以y=1
(2)令y1=y2,即,则x=,y=y,即两种卡收费一
12致;当时,y1>y2,即使用“便民卡”便宜;当时,y<y,即使用“如意卡”便
12宜。
31.提示:(1)由题意可知,当这种鸟类静止时,它的速度为0m/s,此时耗氧量为30个单位,可得,即a+b=0;
要使飞行速度不低于2m/s,即v≥2,所以,即,解得27,即Q≥270。
若这种鸟类为赶路程,飞行的速度不能低于2m/s,则其耗氧量至少要270个单位。
32.提示:(1)由(t为 学 习 时 间),且f(2)=60%,可 得,解得所以
33.提示:(1)由题意可知f(x)=loga(2-3x)有意义,则2-3x>0,即,故函数f(x)的定义域为
(2)易知g(x)=loga(2-a x)-loga(2+a x)。因为2-a x>0且2+a x>0,所以,即函数的定义域关于原点对称。又g(x)=l g oa(2-a x)-loga(2+a x),所以,故g(x)为奇函数。
(3)令μ=2-a x。因为a>0,a≠1,所以μ=2-a x在[2,3]上单调递减。又函数f(x)在[2,3]上单调递增,所以0<a<1。
因为函数f(x)在[2,3]上的最大值为1,所以f(3)=1,即f(3)=loga(2-3a)=1,可得因为0<a<1,所以符合题意。故存在实数,使函数f(x)在[2,3]上单调递增,并且最大值为1。
空间几何体综合演练B卷
一、选择题
1.提示:由圆锥、圆台、圆柱的定义可知,①②错误,③正确。对于④,只有用平行于圆锥底面的平面去截圆锥,才能得到一个圆锥和一个圆台,④不正确。应选B。
2.提示:由题意知,其正视图的面积为当顶点P在底面A B C D上的投影在△B C D内部或其边上时,俯视图的面积最小,最小值为所以三棱锥P-B C D的正视图与俯视图的面积之和的最小值为应选A。
3.提示:A,B,D选项满足三视图作法规则,C不满足三视图作法规则中的宽相等,故C不可能是该锥体的俯视图。应选C。
4.提示:作辅助线(图略),其中O为球心,G,G1分别为正方体上,下底面的中心。设O G1=x,则O B1=S O=2-x。由正方体的性质知,在R t△O BG中,由11,得解得,所以球的半径,故球的表面积为应选D。
5.提示:由三视图可知,该几何体的直现图是五面体D C-A F E B(图略),其中平面A B C D⊥平面A B E F,C D=2,A B=6,E F=4,底面是等腰梯形,高为3,梯形A B C D的高为4,等腰梯形F E D C的高为故三个梯形的面积之和为应选C。

图1
6.提示:多面体A B C D E为四棱锥(如图1),利用割补法可得其体积应选D。
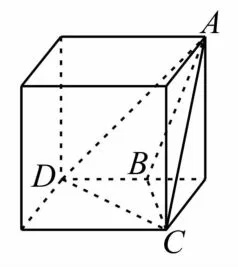
图2
7.提示:由三视图可知,该几何体为三棱锥,记为A-B C D,将其放入棱长为3的正方体中,如图2。故VA-B C D应选D。
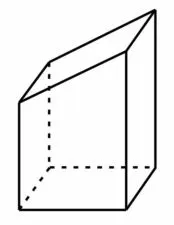
图3
8.提示:根据该几何体的三视图作出其直观图,如图3所示。可以看出该几何体是一个底面为梯形的四棱柱。根据三视图可得该几何体中梯形的上底长为2,下底长为3,高为2,所以该几何体的表面积应选B。
9.提示:将正四面体补成正方体,则正四面体的棱为正方体面上的对角线。因为正四面体的棱长为4,所以正方体的棱长为因为球O与正四面体的各棱都相切,所以球O为正方体的内切球,即球O的直径2R=则球O的体积应选A。
10.提示:取A B的中点为O1。在可知△A B C所在小圆O1是以A B为直径的圆,所以,且又球O的直径P A=4,所以O A=2,可得O O1=且O O1⊥底面A B C。故点P到平面A B C的距离为应选B。
11.提示:将圆柱桶竖放,水面为圆面;将圆柱桶斜放,水面为椭圆面或部分椭圆面;将圆柱桶水平放置,水面为矩形面。所以圆柱桶内的水平面可以呈现出的几何形状不可能是梯形面。应选C。
12.提示应选C。
13.提示:由三视图可得该几何体的直观图(图略)。该几何体是一个棱长为2的正方体上、下各挖去一个底面半径为1,高为1的圆锥后剩余的部分,其体积为应选A。
14.提示:用一个平面去截正方体,截面的情况有四种:①截面为三角形情况,可以是等腰三角形、等边三角形,但不可能是直角三角形;②截面为四边形情况,可以是梯形(等腰梯形)、平行四边形、矩形、正方形,但不可能是直角梯形;③截面为五边形情况,不可能是正五边形;④截面为六边形情况,可以是正六边形。应选A。
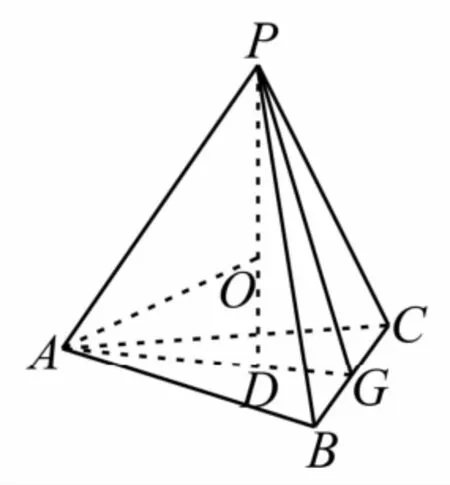
图4
15.提示:正三棱锥P-A B C的直观图如图4所示。作P G⊥C B于点G。设点P在底面A B C内的射影为点D。依题意可得平面A B C。易知正三棱锥P-A B C外接球的球心在P D上,不妨设球心为O,球半径为r。在R t△A O D中,由r2=A D2+(P D-r)2,得,故S=4 πr2=应选B。
16.提示:由题意可知,此几何体是一个三棱柱,三棱柱的高为由于底面是等腰直角三角形,两直角边长为2,所以其面积为由其侧面积为(2+2+可得表面积为2×2+应选A。
17.提示:由俯视图和正视图可知,该几何体可看成是由一个半圆锥和一个三棱锥组合而成的,且三棱锥的一个面恰为半圆锥的最大轴截面。应选D。
18.提示:由三视图可知,该几何体为三棱锥,底面为腰长为2的等腰直角三角形,高为1,则该几何体的体积为应选D。
19.提示:由三视图可知,该几何体为四棱锥,其底面为直角梯形,面积2)×2=3。由该几何体的体积,解得x=1.5。应选C。
20.提示:由三视图易知该几何体为四棱锥,所以,其中S是四棱锥的底面积,即俯视图中四边形的面积,易知S=1,h是四棱锥的高,由正视图和侧视图易知h=1。所以应选C。
21.提示:设球心为O,△A B C的中心为
O′。因为,所以A O′=因为球心到平面A B C的距离为
1,即O O′=1,所以故该球的表面积S=20 π。应选A。
22.提示:正方体的棱长为a,体积V=等边圆柱(轴截面是正方形)的高为2h,体积V=π·h2·2h=球的半径为R,体积故S球<S柱<S正。应选C。
二、填空题
23.提示:设内切球的半径为r。由鳖臑的性质可知,所以4。由S△P C A)·r,可得该鳖臑的内切球半径r=

图5
24.提示:根据三视图可知该几何体是一个三棱锥,记为S-A B C,将该三棱锥放入长方体中,如图5所示。该三棱锥的外接球直径为长方体的体对角线。设球O的半径为R,则(2R)2=22+22+32=17,即,故球O的表面积为4 πR2=17 π。
25.提示:设底面A B C D的中心为O1,四棱锥P-A B C D的外接球的球心为O。易知O在四棱锥的高P O1(或延长线)上。由球的性质可知△O O1A为直角三角形,易得O1A,所以O O=4,所以P O11=4+5=9或P O1=5-4=1。当P O1=9时,四棱锥P-A B C D的体积为当P O1=1时,四棱锥P A B C D的体积为故四棱锥P-A B C D的体积为6或54。

图6
26.提示:由三视图知,该几何体是四棱锥,且四棱锥的一条侧棱与底面垂直,如图6所示。其中P A⊥平面A B C D,可得P A=3,A B=C D=4,A D=B C=5,可 得故该几何体最长的棱长为
27.提示:根据三视图可知该几何体是一个四棱锥,其底面是正方形,侧棱都相等,所以这是一个正四棱锥。其侧视图与正视图是完全一样的正三角形。故侧视图的面积为
28.提示:因为A,B,C,D为球面上不同的四点,所以B,C,D不共线。由A B=A C=A D知A在平面B C D内的射影为△B C D外接圆的圆心,记圆心为O1。设O为球的球心,则O B=O C=O D,故O在平面B C D内的射影也为△B C D外接圆的圆心O1,可知O A⊥平面B C D。又A B=A C=A D=4,所以平面B C D垂直平分线段O A。记△B C D外接圆的半径为r,由勾股定理得r2+,即r2=16-4=12。可知平面B C D被球所截得的图形即△B C D的外接圆,其面积为πr2=12 π。
29.提示:设A A1的中点为N,则MN∥A D1∥B C1,可知平面MNB C1就是过正方体中C1,B,M三点的截面。由A1M=A1N=1,可得同理可得由可得梯形MNB C1的高故所求截面的面积为
30.提示:因为B C⊥C D,所以B D2=B C2+C D2=13,且B D为△B C D外接圆的直径。又A B⊥平面B C D,所以A B⊥B D,则A D为球O的直径,所以2R=A D=可得故球O的表面积S=4 πR2=14 π。
三、解答题
31.提示:(1)四棱锥P-A B C D的直观图如图7所示。

图7
因为四棱锥P-A B C D的高为P A,其底面积为,所以四棱锥的体积V四棱锥P-A B C D,可得故正视图的面积为
(2)过A作A E∥C D交B C于E,则A E⊥B C。根据三视图可知E是B C的中点,可得B E=C E=1,A E=C D=1,B C⊥A E,A B
因为P A⊥平面A B C D,所以P A⊥A D,可得由P A⊥B C,可得B C⊥平面P A E,可知B C⊥P E。
因为D C⊥A D,所以D C⊥面P A D,可得D C⊥P D。因为P A⊥平面A B C D,所以P A⊥A E,可得P E2=P A2+A E2=3,即故四棱锥P-A B C D的侧面积为
32.提示:由题意可设直三棱柱形容器中盛水为V水,三棱柱A B C-A1B1C1的体积为当底面A B C水平放置时,可得当A ABB水平放置时,设水面与11棱B C交于点E,则,而△A B C与△C D E相似,所以,可得,可知D为A C的中点。
