函数应用综合演练A 卷

■卜素英

一、选择题

1.函数f（x）=ex+x-3在区间（0，1）上的零点个数是（ ）。

A.0 B.1

C.2 D.3

2.函数的零点所在的区间为（ ）。

A.（0，1） B.（1，2）

C.（2，3） D.（3，4）

3.在用“二分法”求函数f（x）零点近似值时，第一次所取的区间是（-2，4），则第三次所取的区间可能是（ ）。

4.函数的零点所在的区间为（ ）。

A.（0，1） B.（1，2）

C.（2，3） D.（3，4）

5.某商场销售A型商品。已知该商品的进价是每件3元，且销售单价与日均销售量的关系如表1所示。

表1

请根据表中数据，要使该商品的日均销售利润最大，则此商品的定价（单位：元/件）应为（ ）。

A.4 B.5.5

C.8.5 D.10

6.若函数的一个零点在区间 （1，2）内，则实数a的取值范围是（ ）。

A.（1，3） B.（1，2）

C.（0，3） D.（0，2）

7.已知分段函数f（x）=则函数y=f（x）+3x的零点个数是（ ）。

A.0 B.1

C.2 D.3

8.20世纪30年代，为了防范地震带来的灾害，里克特（C.F.Richter）制定了一种表明地震能量大小的尺度，就是使用测震仪衡量地震能量的等级，地震能量越大，测震仪记录的地震曲线的振幅就越大，这就是我们常说的里氏震级M，其计算公式为M=l gA-l gA0，其中A是被测地震的最大振幅，A0是“标准地震”的振幅。已知5级地震给人的震感已经比较明显，则7级地震的最大振幅是5级地震的最大振幅的（ ）。

A.10倍 B.20倍

C.50倍 D.100倍

9.已知函数f（x）=若函数y=f（2-x2）-f（2x+k）只有一个零点，则实数k的值为（ ）。

A.4 B.3

C.2 D.1

10.设m∈N，若函数f（x）=2x-存在整数零点，则符合条件的m的个数为（ ）。

A.2 B.3

C.4 D.5

11.奇函数f（x），偶函数g（x）的图像分别如图1，2所示，函数f[g（x）]，g[f（x）]的零点个数分别为m，n，则m+n=（ ）。

图2

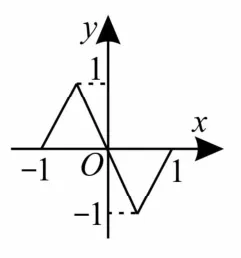
图1

A.3 B.7

C.10 D.14

12.将进货单价为80元的商品按90元一个出售时，能卖出400个，已知这种商品每涨价1元，其销售量就要减少20个，为了赚得最大利润，每个售价应定为（ ）。

A.85元 B.90元

C.95元 D.100元

13.图3所示的是某一容器的三视图，现向容器中匀速注水，容器中水面的高度h随时间t变化的可能图像是（ ）。

图3

14.若函数f（x）=（m-2）x2+m x+（2m+1）的两个零点分别在区间（-1，0）和（1，2）内，则实数m的取值范围是（ ）。

15.已 知 函 数f（x）=2017x+，则关于x的不等式f（1-2x）+f（x）＞6的解集为（ ）。

A.（-∞，1） B.（1，+∞）

C.（1，2） D.（1，4）

16.某工厂产生的废气经过滤后排放，在过滤过程中，污染物的数量p（单位：m g/L）不断减少，已知p与时间t（单位：h）满足，其中p0为t=0时的污染物数量。又测得当t∈[0，30]时，污染物数量的变化率是-10 ln 2，则p（60）=（ ）。

A.150m g/L B .300m g/L

C.150 ln 2m g/L D.300 ln 2m g/L

二、填空题

17.已知λ∈R，分段函数f（x）=若函数f（x）恰有个零2点，则λ的取值范围是18.已知函数的零点为x0，若x0∈（k，k+1），其中k为整数，则

19.渔场中鱼群的最大养殖量为mt，为保证鱼群的生长空间，实际养殖量不能达到最大养殖量，必须留出适当的空闲量。已知鱼群的年增长量yt和实际养殖量xt与空闲率的乘积成正比，比例系数为k（k＞0），则鱼群年增长量的最大值是（空闲率为空闲量与最大养殖量的比值）

20.已知函数f（x）=log2x+2x-m有唯一的零点，若它的零点在区间（1，2）内，则实数m的取值范围是

21.设在海拔x（单位：m）处的大气压强为y（单位：k P a），y与x的函数关系可近似表示为y=100 ea x。已知在海拔1000m处的大气压强为90k P a，则根据函数关系式，在海拔2000m处的大气压强为

22.某工厂常年生产红木家具，根据预测可知，该产品近10年的产量平稳增长。记2014年为第1年，且前4年中，第x年与年产量f（x）（单位：万件）之间的关系如表2所示。

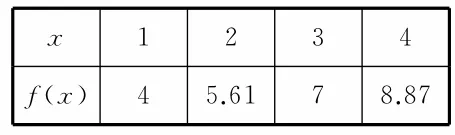
表2

现有函数f（x）的三种函数模型：①f（x）=a x+b，②f（x）=2x+a，③f（x）其中最适合的函数模型的序号为

23.若函数f（x）=4x-2x-a，x∈[-1，

1]有零点，则实数a的取值范围是

24.已知函数2个零点，则实数a的取值范围是

25.某种病毒经30m i n繁殖为原来的2倍，且知病毒的繁殖规律为y=ek t（其中k为常数，t表示时间，单位：h，y表示病毒个数），则经过5h，1个病毒能繁殖的病毒的个数为

26.某汽车销售公司在A，B两地销售同一种品牌的汽车，在A地的销售利润（单位：万元）为y1=4.1x-0.1x2，在B地的销售利润（单位：万元）为y2=2x，其中x为销售量（单位：辆）。若该公司在两地共销售16辆该种品牌的汽车，则能获得的最大利润是万元。

27.已知f（x）是奇函数且是R上的单调函数，若函数y=f（2x2+1）+f（λ-x）只有一个零点，则实数λ的值是

三、解答题

28.设x1，x2分别是函数f（x）=x-a-x和g（x）=xlogax-1的零点（其中a＞1），求x1+4x2的取值范围。

29.已知函数f（x）=

（1）求方程f（x）=3f（2）的解集。

（2）讨论函数g（x）=f（x）-a（a∈R）的零点的个数。

30.为了发展电信事业方便用户，电信公司对移动电话采用不同的收费方式，其中所使用的“如意卡”与“便民卡”在某市范围内每月（30天）的通话时间x（m i n）与通话费y（元）的关系分别如图4，5所示。

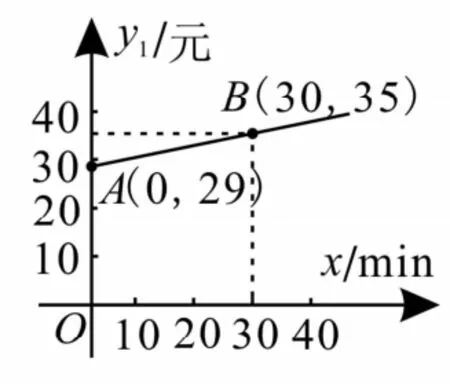
图4

图5

（1）分别求出通话费y1，y2与通话时间x之间的函数关系式。

（2）请帮助用户计算，在一个月内使用哪种卡便宜?

31.候鸟每年都要随季节的变化进行大规模的迁徙，研究某种鸟类的专家发现，该种鸟类的飞行速度v（单位：m/s）与其耗氧量Q之间的关系为（其中a，b是实数）。据统计，该种鸟类在静止的时候其耗氧量为30个单位，而其耗氧量为90个单位时，其飞行速度为1m/s。

（1）求出a，b的值。

（2）若这种鸟类为赶路程，飞行的速度不能低于2m/s，则其耗氧量至少要多少个单位?

32.学习曲线是通过对大量有关资料、案例的观察、分析、研究，首次发现并提出来的。已知某类学习任务的学习曲线为f（t）=（其中f（t）为掌握该任务的程度，t为学习时间），且这类学习任务中的某项任务满足f（2）=60%。

（1）求f（t）的表达式，计算f（0）并说明f（0）的含义。

（2）当学习时间t∈（1，2）时，学习效率最佳。当学习效率最佳时，求学习曲线相应的取值范围。

33.已知函数f（x）=loga（2-a x）。

（1）当a=3时，求函数f（x）的定义域。

（2）若g（x）=f（x）-loga（2+a x），试判断g（x）的奇偶性。

（3）问是否存在实数a，使函数f（x）在[2，3]上单调递增，并且最大值为1。若存在，求出a的值;若不存在，说明理由。