观测噪声方差变化条件下系统状态估计方法
2019-11-07宋婉娟
宋婉娟 ,张 剑
(1.湖北第二师范学院计算机学院,湖北 武汉 430205 ;2.武汉体育学院体育工程与信息技术学院,湖北 武汉 430070)
0 引言
非线性系统状态估计问题是工程应用中的难点和瓶颈,备受研究人员关注[1-3],但是由于该类系统参量的未知性,很难建立精确的数学模型,目前常用的解决方法主要是采用滤波估计,数值逼近的思路解决。例如,扩展卡尔曼滤波(Extended Kalman Filter,EKF)[4-7],通过对非线性系统进行一阶泰勒近似,将非线性系统进行局部线性近似处理,虽简单易行,但存在明显的截断误差,噪声敏感性强;无迹卡尔曼滤波(Unscented Kalman Filter, UKF)[8-10],通过对模型统计参量的非线性变换,实现系统的高阶近似,但是其估计精度严重依赖于系统初值和观测噪声,当噪声参量时变情况下跟踪精度会降低;粒子滤波(Particle Filter, PF)[11-15]通过粒子加权求和的方法对系统积分进行拟合,在粒子数足够多的情况下是可以无限逼近系统真实状态的,但是该方法的滤波精度和实时性之间的矛盾至今尚未有效解决,限制了其工程应用。针对这些问题,文献[16]采用高阶球面积分传播容积点的思想提出了容积卡尔曼滤波(Cubature Kalman Filter, CKF)方法,对状态的均值和协方差进行非线性传播,同EKF、UKF以及PF等非线性滤波方法相比,不仅提升了滤波精度,计算的复杂性也大大降低,在目标跟踪、状态估计等领域得到了广泛的应用。但是标准CKF方法严重依赖于精确的状态模型和噪声统计特性[17-19],而在实际的工程应用中很难满足,特别是观测噪声方差,具有较强的时变特性,很难满足噪声方差统计特性精确已知的要求[20],限制了其在工程中的推广应用。
针对观测噪声方差时变情况下,非线性系统状态估计精度不高的问题,本文借鉴计算机视觉领域的变分贝叶斯方法[21-24],将其引入到CKF的框架内,并应用于非线性系统估计。首先,基于变分贝叶斯进行模型参量和噪声统计特性的实时估计,并将估计结果引入到CKF的滤波过程,进行非线性系统的在线预测和估计。由于实现了模型参量和噪声特性的在线动态更新和估计,能够很好地适应无法预先精确获取信息时变系统,有效扩展了CKF的应用范围。最后,基于计算机仿真对本文方法进行了详细的性能分析。
1 非线性系统模型及标准CKF算法说明
1.1 非线性系统模型
常用的非线性系统状态方程可以表示为:
(1)
式(1)中,f(xk-1)和h(xk)分别表示状态过程和观测过程的非线性函数,wk~N(0,qk)和vk~N(0,rk)分别表示状态噪声和观测噪声,二者均假设服从高斯分布,其中,qk和rk分别表示过程噪声和观测噪声的协方差矩阵。因此,可进一步将将式(1)的非线性系统模型表示为:
(2)
因xk符合均值为mk,方差为Pk的高斯分布,即xk~N(mk,Pk),则k-1时刻的先验概率为:

p(xk|z1:k)=N(mk,Pk)
1.2 标准CKF算法原理
针对式(2)描述的非线性系统方程,可将标准CKF的算法概括为预测和更新两个过程,具体的实现描述为[25]:
预测:
(3)
(4)
(5)
(6)
更新:
(7)
(8)
其中,h(·)为式(1)中所示的观测过程非线性传递函数,[1]=[I,-I],I为单位矩阵。
(9)
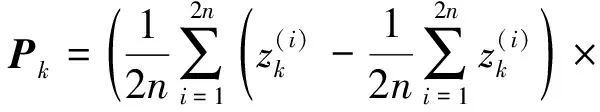
(10)
(11)
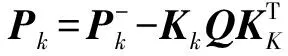
(12)
1.3 变分贝叶斯参数估计
获取观测信息Z以后,可以将状态变量x的后验密度按照贝叶斯准则表示为:
(13)
其核心是计算边缘似然函数p(Z),线性条件下可以通过解析计算的形式获取,但是在非线性情况下,很难获取解析解,文献[25]提出采用变分贝叶斯思想,通过引入近似分布函数q(x),将式(13)重新表示为:
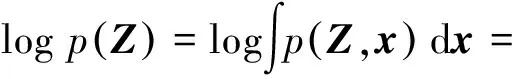
(14)
且:

(15)
(16)
通过偏导计算,可将F(q(x))的极值计算为:
(17)
因此,可以将这种参量估计方法理解为在给定先验观测信息的条件下,联合初始条件对F(q(x))进行迭代估计,计算极值的过程。
2 观测噪声方差时变条件下系统状态估计方法
从标准CKF的计算过程中可以看出,其观测噪声是已知且不变的,这一点的假设不符合实际的工程应用环境。因此,本文主要针对观测噪声时变情况下的滤波问题进行分析,本文的主要改进思想是对观测噪声特性和系统状态变量进行联合在线估计,同现有的方法相比,主要有以下两点创新:
1) 在预测步骤中对噪声的方差进行动态建模,并采用变分贝叶斯方法在更新步骤中迭代地估计观测噪声的方差;
2) 将估计的噪声统计特性和状态参量引入到CKF滤波框架,实现了非线性系统的精确滤波和估计。
假设获取k-1观测后,可将两者的联合概率分布函数表示为:
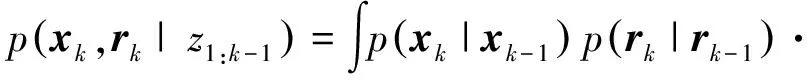
(18)
k时刻观测信息获取后,可表示为:
(19)
为了快速简洁的计算积分,采用变分贝叶斯的方法进行次优逼近,根据文献[26]的研究,可将式(19)表示为:
p(xk,rk|z1:k-1)=p(xk|z1:k-1)p(rk|z1:k-1)=
(20)
根据式(14)—式(17)的分析,引入q(xk,rk|z1:k)近似p(xk,rk|z1:k),在两者独立的情况下,可将联合概率表示为:
q(xk,rk|z1:k)=q(xk|z1:k)q(rk|z1:k)
(21)
则可将状态变量表示为:

(22)
系统观测噪声方差表示为:
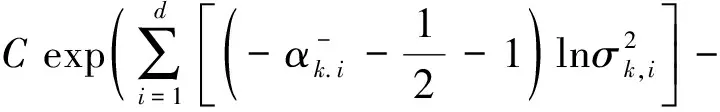
(23)
假设参数服从高斯分布,则可表示为[27]:
q(xk|z1:k)=N(xk|mk,Pk)
(24)

(25)
(26)
(27)
(28)
假设参量服从逆Gamma分布,则可表示为:
(29)
(30)
(31)
则
(32)
根据CKF的采样原理,则期望的计算可以展开为:
Exk[((zk-hk(xk))i)2]=
(33)
3 实验与结果分析
为验证本文方法的性能,采用振动系统中常用的非线性系统方程,其离散形式的状态模型和观测模型如式(34)所示[28]:
(34)
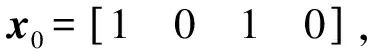

(35)

(36)
实验中为便于分析具体效果,将估计结果同传统的CK方法进行比较,具体的估计结果如图1、图2和图3所示,分别展示了在不同的观测噪声情况下的跟踪结果,并给出了估计误差。其中,图(a)的横轴表示具体的运行时间,纵轴为状态的幅值,图(b)的横轴表示具体的运行时间,纵轴为状态估计的相对误差幅值。

图1 rk=1时跟踪结果Fig.1 Estimation results when rk=1

图2 过程噪声固定观测噪声时变的跟踪结果Fig.2 Estimation results when the process noise is constant and the observation noise is time-varying
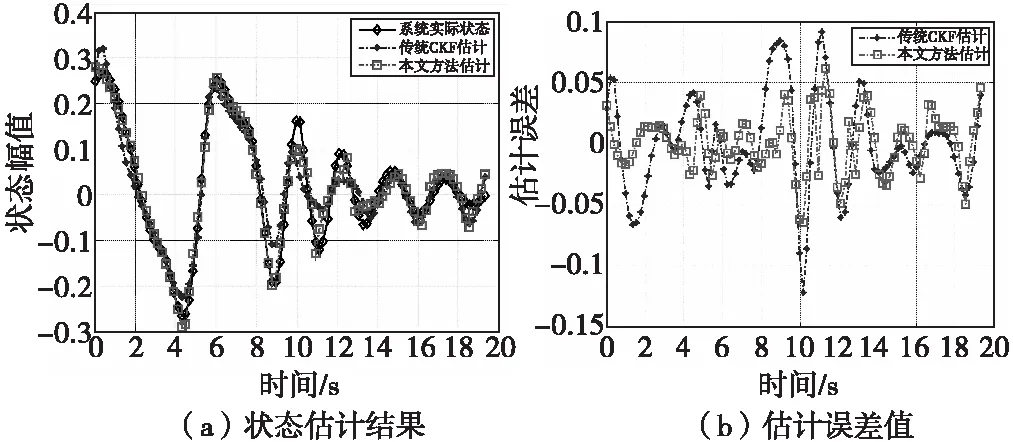
图3 rk=5时跟踪结果Fig.3 Estimation results when rk=5
从图中可以看出,随着观测噪声的增加,传统CK滤波估计方法的估计精度逐渐降低,估计误差明显增加,但是本文方法仍然保持了较好的估计精度。其主要原因是因为传统CK方法缺少系统观测噪声的实时信息,随着迭代估计的时间递推,出现了估计误差的累计效应。这一点从各个误差曲线的幅值分布状态均可以明显看出。而本文方法由于采用了状态和观测噪声统计特性的联合估计方法,获取了观测噪声的实时信息,保证了较高的估计精度。但是随着观测噪声方差的逐步增加,本文方法的估计精度也有所降低,这一点主要是因为观测噪声增加,引起了观测参量模型的漂移,至于观测模型漂移问题对估计精度的影响,作者在后续的研究中会进一步分析,在本文中就不详细分析。
4 结论
针对噪声动态时变情况下的非线性系统状态估计问题,本文提出了一种观测噪声方差变化条件下系统状态估计方法。该方法采用变分贝叶斯滤波对系统的状态和观测噪声进行在线实时估计,保证了最新观测信息对参量的修正作用,通过将估计的结果引入到传统容积卡尔曼滤波框架内实现非线性系统状态的迭代估计。仿真结果表明,本文方法较好地改善了噪声统计特性时变情况下的估计精度,有效扩展了容积卡尔曼滤波在非线性系统状态估计方法中的应用范围。
