基于FLUENT和ADAMS的外弹道加速度仿真
2019-11-07王莎莎张东东李新娥沈大伟刘奇峰
王莎莎,张东东,李新娥,沈大伟,刘奇峰
(中北大学仪器科学与动态测试教育部重点实验室,山西 太原 030051)
0 引言
外弹道学是研究弹箭与发射装置的作用力脱离之后在空中的运动规律和相关问题的一门学科[1]。现代战争不断地要求炮弹增加射程,落点精确和毁伤威力,因此,研究外弹道弹丸飞行姿态和稳定性,越来越成为当今国际发展的总趋势[2]。
目前,在外弹道的研究上主要使用的方法有风洞吹风法、工程计算法、实验测量法。比如1 200×1 200 mm2和2 400×2 400 mm2的超音速风洞,直径达1 000 mm2的高超音速风洞为我国新型飞行器的研制提供了充足的技术保障[3]。但是,风洞吹风的方法能耗高、周期长、测试条件复杂、易受外界干扰、成本高。常用的工程计算方法主要有二次激波理论、薄翼型理论、二次混合扰动、二次激波膨胀、锥形流理论、牛顿理论、小扰动线化等多种理论[4]。由于几何形状的不同,使用工程计算的方法得到的数据在精度上往往不是很高,对弹体的某些部分和某些时段的估算也存在误差。在弹箭外弹道测量上,裴东兴、岳晗等人提出了使用地磁薄膜线圈磁传感器测试弹箭飞行姿态参数的方法[5]。沈大伟、边玉亮等人提出了使用地磁薄膜线圈测试旋转弹章动参数的方法[6]。其测试方法是将测试仪器系统直接放置在实际运动着的被测体内或被测环境中,使得仪器系统与被测对象承受相同的恶劣环境影响,并实时、实况、准确地获取动态参数,此测试方法具有体积小、低功耗、稳定、抗冲击、抗高过载等技术特点。但是此方法一般在测试时环境极其恶劣,并且测试成本较高。针对上述问题,提出了基于FLUENT动力学仿真软件和ADAMS运动学仿真软件相结合的弹丸外弹道仿真测试方法。
1 旋转弹外弹道模型
无控旋转弹在空中受到的空气动力不仅影响着弹丸的飞行姿态,而且影响打击目标的精准性。因此,建立准确而又简单的旋转弹动力学模型,是对弹丸的外弹道稳定性分析和控制系统设计的基础[7]。
1.1 弹丸基本假设
为了达到预期的仿真效果,需要对弹丸做一定的假设。这样的假设不仅可以将问题变得简化,同时也可以将整个弹丸的运动规律展现出来。
1) 弹丸的外形和质量相对于弹轴分布是对称的,弹轴为惯性主轴且质心位于弹轴上;
2) 弹丸的运动可以看成全部质量集中于质心的一个质点的运动;
3) 攻角很小或者不存在,使得线性关系成立;
4) 地表为平面,重力加速度不变,方向铅直向下;
5) 气象条件为标准条件。
1.2 弹丸受力分析
弹丸在出膛后,不会再受到火药的压力,而是受到空气的阻力。图1为高速旋转弹在受到空气阻力和力矩时的情况。在图中可以看出总空气动力FN可分为与速度方向相反的水平分力Rx和竖直速度方向的竖直分力Ry(或由沿弹轴的轴向力RA和垂直于弹轴的法向力Rn合成的).由于俯仰力矩Mz的作用,使得弹的轴向方向远离速度矢量方向,弹丸产生一个攻角δ的变化。

图1 旋转弹受力示意图Fig.1 Schematic diagram of the force of the rotating bomb
1.2.1不考虑攻角时的受力分析
弹丸在空中飞行时,由于空气具有黏性,弹表会附带一层空气,和弹丸共同运动,这种阻力称为摩阻。气流达到一定值后,弹丸尾部的流线会与弹丸分离,形成旋涡,这种阻力称为涡阻。在超声速条件下,弹尾将会出现大量的旋涡,其弹头和弹尾由于剧烈压缩空气,产生接近于锥形的空气层,此阻力称为波阻。由此可知,弹丸在飞行时,同时受到摩阻、涡阻和波阻的影响。如式(1)、式(2)所示:
(1)
Cx0(Ma)=cxf+cxb+cxw
(2)
此时所产生的加速度由式(3)所示,ax体现的是空气阻力对弹丸质心速度大小和方向的改变[8]。
(3)
式(1)—式(3)中,ν为弹丸相对空气的速度,ρ为空气密度,S为特征面积,cx0(Ma)为阻力系数,cxf为摩阻系数,cxb为涡阻系数,cxw为波阻系数。
1.2.2考虑攻角时的受力分析
如图1所示,当攻角存在时,气流在弹丸的迎风侧和背风侧的变化关于弹轴是不对称的。迎风侧空气受到弹体挤压而风压大,背风侧空气受到拉力而风压小,这种压差随着速度和攻角的增大导致总空气动力显著增大,并且它的作用方向既不沿着弹轴或速度的反方向也不通过弹丸瞬时质心,而是在攻角平面内偏在弹丸背风面与弹轴速度线的一侧[9]。由图1可以得到Rx、Ry、RA、Rn的关系为式(4)所示:
(4)
将式(4)换成气动力系数即为式(5)所示:
(5)
式(5)中,cx为阻力系数,cy为升力系数,cA为轴向力系数,cn为法向力系数。
总空气动力FN对弹丸质心作用的力矩为式(6)所示:
(6)
将总空气动力FN以作用于压心的二分力Rx、Ry代替,可得出俯仰力矩Mz和升力Ry、阻力Rx和压心P到质心O之间的距离h之间的关系。如式(7)、式(8)所示:
Mz=Rycosδ+Rxsinδ
(7)
mz=(cycosδ+cxsinδ)h/l
(8)
从式子中可以看出,其它条件不变的话,俯仰力矩是Ma和攻角δ的函数,l为参考长度,mz为静力矩系数。
1.2.3压力中心
由图2可以看出压力中心的位置处于弹丸质心和头部之间的连线上。实验证明,弹丸的压心位置不仅随马赫数变化而变化,也随攻角δ大小而改变,根据旋转弹丸在风洞中吹风的实验结果,压心随着马赫数的增大向弹底移动,使得实际的压心、质心距h减小[10]。

图2 弹丸各部尺寸图Fig.2 Dimensions of the various parts of the projectile
对于旋转弹,压力距离质心的距离可用高巴尔公式进行估算,如式(9)所示:
h=h0+0.37ht-0.16d
(9)
式(9)中,h0表示头部底端至质心的距离,ht表示弹丸头部的长度。
除上节所介绍的弹丸受力外,弹丸在外弹道飞行过程中,还受到重力的影响。标准重力加速度为:北纬45°,零海拔:gNo=9.806 65 m/s2,g=gNof(y,Λ)。y表示高度,Λ表示纬度。
2 外弹道仿真
2.1 弹丸外流场仿真
FLUENT是一个用于模拟和分析复杂几何区域内的流体流动和传热现象专用软件,具有广泛的物理模型,能够快速、准确的获得CFD(流体动力学)分析结果。在仿真的过程中,必要时还要对网格进行细化,改变数值和物理模型,使得仿真条件更加接近真实工况,得到更为精确的结果。
首先对无控旋转弹建立一个长方体的计算域,如图3所示。在GAMBIT中进行弹丸模型的网格划分,如图4所示。计算出不同工况下(不同马赫数和不同攻角)的外部绕流场。在获得流场的压力分布之后,FLUENT会自动对弹丸的表面进行积分,从而求得弹体和各个位置表面受到的空气动力。为了简化分析,只观察空气阻力和俯仰力矩的数值。除此之外,弹丸运动速度通常都超过了声速,甚至达到几倍音速,因此弹丸周围的流场为超音速气流,密度的变化不可忽略。因此,将仿真定义为三维弹丸的外部超声速可压缩绕流流场的数值分析。

图3 计算域的建立Fig.3 Establishment of the calculation domain

图4 弹丸的网格划分Fig.4 Meshing of the projectile
由于绕流场的计算要求在弹丸附近布置的网格足够密,才能准确的获得所需要的参数,同时计算域又要足够的大,以适应远场边界条件,避免流场中压力波等边界反射引起数值计算的不稳定[11]。在计算域的中间位置再设置一个小圆柱体,将里边的网格进行加密处理,外边的网格划分上较为稀疏,在保证了计算精度的同时,又加快了仿真进度。
将划分好网格的模型文件导入到FLUENT中,本次仿真选用密度基耦合显示求解器,S-A湍流模型,在流体物理属性定义上,选择了空气,满足萨兰德定律计算粘性,将定压比热和热传导率都设置为常数。在密度基的求解过程中,由于会涉及接下来的压力输入和数据对比,为了与边界条件的设定值表述习惯相一致,将参考压力置零。设置的边界条件参数如表1所示。

表1 边界条件参数设定值
在表1中,由于在模型的建立过程中,坐标系X轴正向的选择是弹尾朝向弹头,与来流气体相对弹丸的运动方向刚好相反,因此横坐标添加负号。
完成上述的所有步骤后,对控制参数进行相关的设定,完成整个仿真。得到1.5Ma和4°攻角下的外流场仿真,进而得出速度云图,如图5所示。
从云图中可以看到,高速飞行的弹丸,其弹表和弹尾受到摩阻、涡阻的影响(弹尾波显示)。由于弹丸周围的流场为超音速气流,弹头和弹尾有相似于锥形的空气层。这与之前的空气阻力分析相一致。并且由于攻角的存在,使得弹丸上下两表面产生了明显的不对称,这与分析和实际测试相一致。

图5 速度云图Fig.5 Speed cloud
在FLUENT软件建立的模型基础上,通过修改边界条件,分别计算出不同攻角和马赫数下弹丸的空气阻力和俯仰力矩。如表2、表3所示。
从表2、表3中可以看出,空气阻力的大小受到攻角的影响不大,主要受马赫数值的影响;而俯仰力矩同时受到攻角和马赫数的影响。
2.2 弹丸运动学仿真
在FLUENT仿真的基础上,利用ADAMS运动学仿真软件的仿真过程可视化特性,可以对弹的整个外弹道过程进行跟踪观察和测量,并得出相应的运动曲线图。首先建立弹体的三维模型,将模型导入ADAMS中得到图6。

表2 不同攻角和马赫数下的空气阻力值

表3 不同攻角和马赫数下的俯仰力矩
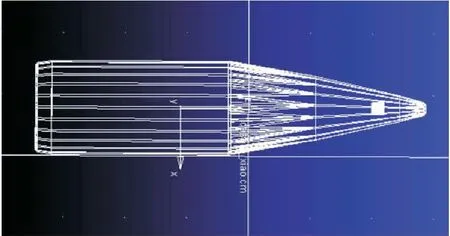
图6 ADAMS中的模型图Fig.6 Model diagram in ADAMS
由于本次实验所用的测试装置为弹载测试仪,因此在仿真时也需加入测试装置。为了在不影响整个弹丸的质量和质心的基础上,需要将测试仪做到小型化。因此在仿真时用一个小圆柱体模型代替,如图6弹头小方块显示。
在ADAMS中对弹丸进行参数设定,总质量为5.86 kg,质心位置为118.5 mm,质心坐标为(0,0,0),初速为980 m/s,转速为2 513.27 rad/s,射角为21°。重力加速度g恒定为9.806 65 m/s2,方向铅直向下,得到设置完参数的模型图7。

图7 设置完参数的模型Fig.7 Model for setting parameters
2.3 弹丸仿真曲线分析
在ADAMS将设置完参数的模型施加之前分析的载荷后进行仿真,就可以得到弹丸在外弹道飞行过程中的速度和加速度仿真曲线,如图8和图9所示。
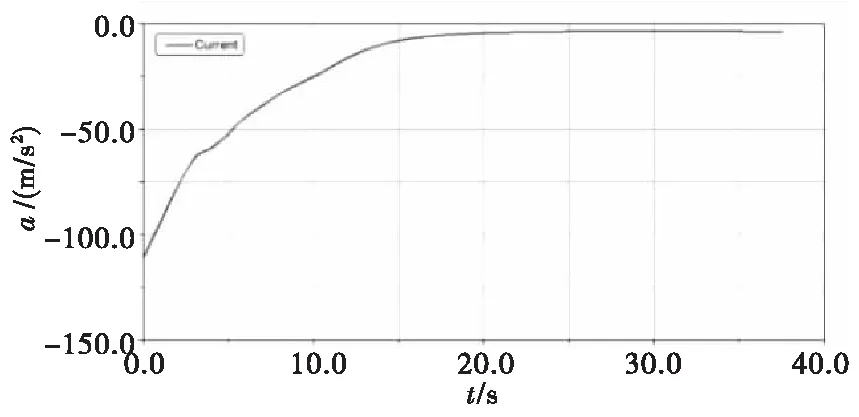
图8 加速度仿真曲线Fig.8 Acceleration simulation curve

图9 速度仿真曲线Fig.9 Speed simulation curve
由仿真曲线可以看出,飞行阶段的加速度曲线呈现负值,这是由于施加载荷时,将指向弹丸头部方向定为正向,因此加速度方向与速度方向相反。外弹道加速度值由最开始的-117.10 m/s2快速下降到最高点的-8.18 m/s2后又平缓的下降至29.6 s的-3.263 m/s2,后期增加到落地前的-3.498 m/s2,弹丸外弹道的飞行速度由最开始的980 m/s下降到26.4 s处248.2 m/s之后速度小幅度的增加到267.2 m/s,这是由于弹在飞行的后期,飞行处于平稳阶段,速度降低,所受的飞行阻力降低,重力弹在飞行爬升阶段的阻力变成了下降阶段的动力,使速度有所增加。
3 弹丸实测曲线分析
靶场进行发射实验时,将弹载测试仪置于实际弹丸中,弹载测试仪底部中心安装加速度传感器,用于测量弹丸在外弹道飞行过程中所受的空气阻力引起的加速度变化[12]。通过加速度计测得加速度实测曲线,如图10所示。对所测的加速度实测曲线进行滤波后得到加速度滤波曲线,如图11所示。通过对加速度曲线积分,得到速度曲线,如图12所示。

图10 加速度实测曲线Fig.10 Acceleration measurement curve

图11 加速度滤波曲线Fig.11 Acceleration filter curve
由图10可以看到,实测曲线中存在很多的杂波,对其进行滤波处理后可以看到加速度值由最开始的-105.7 m/s2快速下降到最高点的-10.2 m/s2后又平缓的下降至29.6 s的-7.436 m/s2,最后变为-5.23 m/s2。
将加速度实测曲线进行积分后,得到速度曲线。由图12可以看出,弹丸速度由最开始的981.3 m/s下降到26.4 s处262.3 m/s,最后变为239.1 m/s。
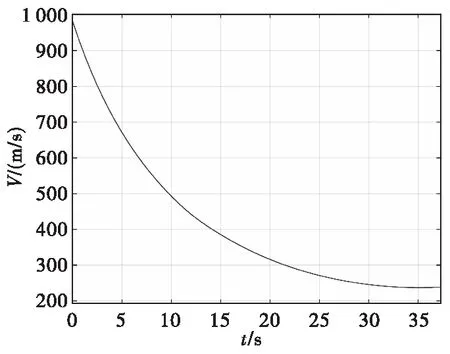
图12 速度曲线Fig.12 Speed curve
由实测曲线和仿真曲线进行对比,发现弹在飞行爬升阶段持续时间低于下降的阶段,整个外弹道的持续阶段为37.616 s。弹丸在16.2 s飞到弹道最高点,由于加速度计本身的原因,使得在弹丸飞行过程中的爬升段在0~16.2 s内,加速度实测值小于实际仿真值,在弹丸飞行过程中的下降段16.2~37.616 s内,加速度实测值大于实际仿真值,因此导致加速度的测试曲线与实际仿真曲线不完全相同,进而导致速度的测试曲线与实际仿真曲线不完全重合。
由实测加速度、速度曲线和仿真得到的加速度、速度曲线可以看出,弹丸在实际飞行中的加速度、速度的变化与仿真得到的变化规律基本保持一致,都是前期曲线比较陡,后期比较平缓。
4 结论
本文提出了无控旋转弹外弹道仿真方法,该方法在建立弹丸受到的空气力和力矩的基础上,运用FLUENT动力学仿真软件对弹丸飞行过程进行仿真。得到了不同马赫数和不同攻角下弹丸受到的空气阻力和俯仰力矩,将这些参数带入到ADAMS运动学仿真软件中,在一定的初始条件下,完成对无控旋转弹的外弹道过程的仿真,得到速度和加速度仿真曲线。并与实测曲线进行对比,发现仿真曲线和实测曲线基本一致。
