调频引信的指数型回波建模方法

智小军，周守锋，黄 辉

(西安机电信息技术研究所，陕西 西安 710065)

0 引言

基于线性调频连续波(LFMCW, Linear Frequency Modulation Continuous Wave)体制的调频引信利用差频回波中各谐波与距离的线性对应关系完成对炸高的连续测量[1]，其距离分辨率取决于调频带宽[2]。差频回波是由调频引信射频端的三角波调制信号与经过目标反射的三角波信号通过混频器的差拍得到，当三角波发生器所产生三角波调制信号的线性度较理想时，距离分辨率仅与调频带宽有关。在实际使用过程中，因成本和体积的限制调频引信通常会使用基于RC充放电路的三角波发生器，所产生三角波调制信号具有一定的指数非线性度[3]，造成差频回波中各谐波与距离线性对应关系恶化，可能影响到了调频引信的距离分辨率[4]。

文献[5]中对二次曲线甚至高阶次曲线[6]的误差函数进行了分析，即线性频率上因运放或VCO器件的因素造成畸变，通过该类型差频信号数学模型的推导在不同非线性度条件下定量分析了距离分辨率的恶化程度[7]。文献[8]中的误差函数则是正弦信号，即在线性频率上附加了一个有若干半周期整数倍的正弦干扰[9]，并推导出与该正弦波形参数有关的实际距离分辨率计算公式[10]。文献[11]意识到在实际工程中无法得到理想的线性调频信号，提出了一种NLFM(非线性调频)引信探测体制，引入调制系数参数描述非线性并分析了其优越性[12]，但实际工程中极少用到甚至不易得到该类型的调制波形[13]。文献[14]推导出了调频引信瞬时相位的数学模型，但该模型是基于理想线性条件下得出的[15]，无法对因采用RC三角波发生电路产生的指数型非线性进行分析。针对传统调频引信因使用RC三角波发生电路会引起回波的指数非线性变化，因缺乏相应回波模型而无法定量分析的问题，本文提出了调频引信的指数型回波建模方法。

1 调频引信测距原理

1.1 调频引信测距原理

典型调频引信工作原理框图如图1所示。通过零差拍工作方式，将产生的三角波调频信号同时送至发射天线和混频器本振端口，与经目标反射的延时回波差拍之后得到差频信号，通过距离(延时)与差频信号的频率线性对应关系实现测距。不失一般性以三角波的上升段为例，且不考虑幅值和初始相位，令中心频率为f0，调频带宽为B，调频周期为T，调频斜率为k=2B/T，距离R处的目标引起的时延差为τR=2(R-vt)/c，v为相对运动速度，c为光速。用下标i表示si(t)为差频回波信号：

(1)

忽略τR2项的影响，对该式中的相位做微分后可得差频频率fi：

(2)

(3)

(4)

可见，理想线性条件下的三角波零差拍测距精度仅与调频带宽有关。

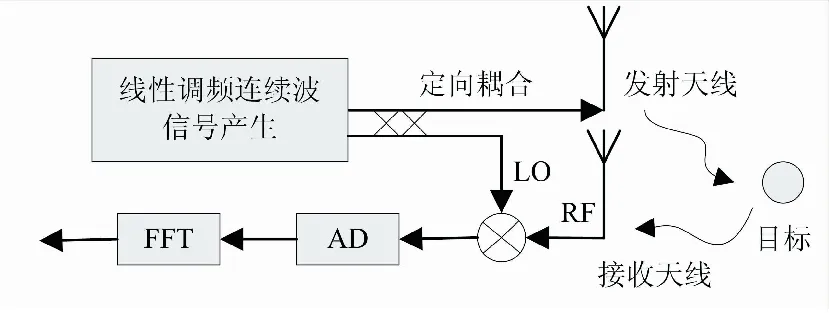
图1 零差拍调频引信工作原理框图Fig.1 Schematic block diagram of zero beat-frequency LFMCW fuze

1.2 非线性分析

实际应用时三角波调制信号会叠加各种非线性干扰，应考虑其对距离分辨率的影响。令e(t)为发射调制频率信号的非线性干扰项，则e(t-τR)为接收频率信号的非线性干扰项，经过接收机零差拍处理后得到差频信号中的非线性干扰频率差拍信号表达式为ei(t)=e(t)-e(t-τR)。实际系统中非线性误差函数满足连续可微的条件，故利用拉格朗日中值定理可简化为ei(t)=e′(t)τR。e′(t)为e(t)的一阶导数。对ei(t)所表示的非线性频率误差函数积分后即可得到非线性误差信号的相位表达式：2πe(t)τR，将该式代入式(1)可将差频回波信号数学模型修正如下：

(5)

对比式(1)和式(5)，可知s1(t)为理想线性条件下的差频信号，而s2(t)即为引入的非线性调制干扰项，导致si(t)成为一个调相信号，此时将无法得到式(2)—式(4)的对应关系。实际上，由于时域上二者是相乘关系在频域上则是完成了卷积运算，相当于在理想目标回波谱附近引起附加的非线性调制边带，展宽后目标差频回波谱的具体大小与e(t)有关。非线性频率干扰项e(t)在每个调制周期的起始和结束点均为0，在每个调制周期内描述为偏离线性频率的大小，利用e(t)定义调频线性度L[16]：

(6)

e(t)max为相对于理想线性频率的最大频率偏离量。结合式(5)和式(6)可知，存在非线性频率干扰的条件下，距离分辨率不仅与调制带宽有关系，还应考虑调频线性度带来的影响。

2 调频引信的指数型回波建模方法

调频引信因使用RC三角波调制信号发生电路使得e(t)为指数型非线性频率信号,式(5)中的非线性频率信号在LFMCW雷达中常被当作二次/高阶曲线或正弦信号进行分析，无法适用于调频引信。为此本文提出调频引信的指数型回波建模方法，并分析了指数非线性对回波频谱和距离分辨率带来的影响。

2.1 指数型回波建模

本文首先给出周期性指数型三角波调制发射信号的频率分段解析式，对其在每个调制周期内进行定积分后归纳出连续性瞬时相位的一般解析式，该解析式与其相应延时信号作差拍处理后即可得到调频引信的指数型回波模型，在此基础上分析了指数非线性对距离分辨率的影响并给出了新的计算方法。所建模型可使回波信号具有模拟信号应有的连续性，避免出现数值仿真计算不收敛以及因相位不连续出现的频谱杂散问题。瞬时相位是由调频频率信号在各相应周期内积分得到的，为此首先给出如式(7)所示周期性指数型三角波调制频率信号解析式，该式因使用了基于RC充放电电路的三角波发生器使所产生三角波具有指数非线性。对该式积分即可得到发射信号的瞬时相位，对发射信号瞬时相位延时后得到目标反射信号瞬时相位，将发射和反射信号瞬时相位相减后即可得到差频回波信号的瞬时相位数学模型。

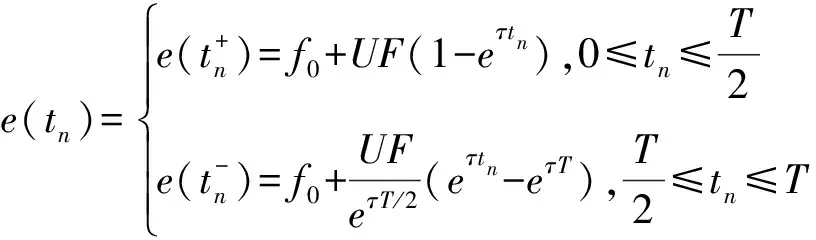
(7)

式(7)中，f0为中心频率，U为充电电压，F为压控振荡器调频系数，单位为MHz/V，τ=-1/RC为时间常数，n表示当前所处调制周期位置，即tn=t-nT∈[0,T]。具体推导过程如下：

1) 设发射初始相位为0；

2)n=0时，0≤t0≤T。在第一个调制周期上升段的瞬时相位为：

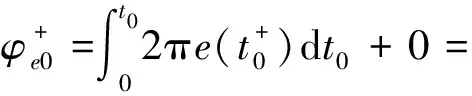
(8)

式(8)中，ω0=2πf0。在上升段结束点即t0=T/2时的瞬时相位为：

(9)

3) 在第一个调制周期下降段的瞬时相位为：

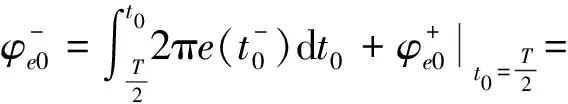
(10)

在下降段结束点即t0=T时瞬时相位为：

(11)

4) 依次令n=1,2,…，即可得到第n个调制周期的发射信号瞬时相位一般表达式：

(12)

5) 目标反射信号瞬时相位为：

φer(tn)=φet(tn-τR)

(13)

6) 差频回波信号的瞬时相位则为：

φei(tn)=φet(tn)-φet(tn-τR)

(14)

7) 最终可得到指数型差频回波信号数学模型为(暂不考虑幅度起伏)：

sei(tn)=ejφei(tn)

(15)

对比式(15)与式(1)可知，式(15)所表述信号函数具有明显的指数型非线性特性，且考虑了其周期性从而保证了各周期之间相位的连续性，通过基于该式的数值仿真分析可以更真实、定量地分析指数非线性对调频引信距离分辨率的影响。

2.2 指数非线性分析

相应的，为从理论上定性分析式(15)所表达指数型回波对调频引信距离分辨率的影响，这里将式(7)代入式(5)整理后得：

(16)

显然因指数非线性使三角波差频回波信号成为一个调相信号，而ej2πe(tn)τR就是这个调相波的复包络。由于其周期也为T，故此时差频回波信号对应距离R处的谐波已被该复包络在附近谐波位置展宽，从而无法分辨出原谐波所对应距离R。式(3)修正为式(17)所表达的实际距离分辨率：

(17)

∂fi=2(2πe(t)max)τR/T

(18)

又结合式(6)即可将式(17)简化为：

∂R=πLcτR

(19)

可见在指数非线性条件下应由式(4)改为式(19)计算实际距离分辨率，根据以上分析可知：

1) 当L足够小时f=f，此时距离分辨率取决于带宽；反之当L增大到一定程度后，距离分辨率与调频带宽无关，由调频线性度L决定。

2) 在调频线性度L一定的情况下，距离分辨率还与目标距离有关，目标距离越大，回波时延τR就越大，距离分辨率就越低。

3 仿真验证

通过与理想线性回波模型的仿真结果对比可验证所建立调频引信指数型回波模型的有效性。本文建立调频引信系统模型参数如下：f0=24 GHz,T=5 μs，目标初始距离为10 m，相对运动速度400 m/s。调制周期一定时，RC电路的充放电时常也就固定下来，此时充电电压U值决定带宽B，而此时在不同B值时相应的指数型调制三角波线性度L也会跟着变化。因此只要分析在不同B值时，系统相应的线性度以及距离分辨率情况。

3.1 调制带宽B=40 MHz

此时式(1)和式(16)描述的理想线性和指数非线性条件下的三角波调制频率波形如图2所示。

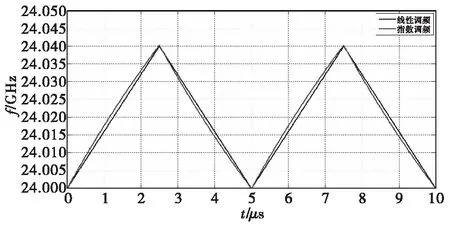
图2 40 MHz调制带宽时的发射频率曲线Fig.2 Transmitted frequency curve when B=40 MHz

此时指数频率调制的线性度较好，较为接近线性调制频率曲线，由式(6)计算得L≈5%。对上图中两条曲线分别与延时后的回波混频后可得差频频率曲线如图3所示。

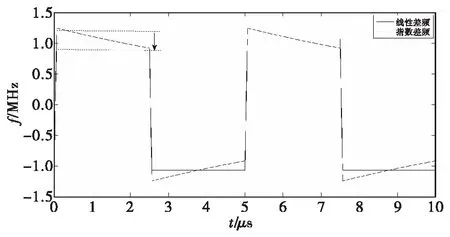
图3 40 MHz调制带宽时的差频频率曲线Fig.3 Difference frequency curve when B=40 MHz

由式(3)可计算得到此时对应10 m处的差频为1.066 7 MHz，而指数差频很明显已不是一根谱线而是有一定的宽度，约为320 kHz。用调制频率的整数倍来考核所展宽程度时，可得：n=320/200=1.6。同时将L≈0.05代入用式(18)所表达的实际带宽，并与理想谱线(近似为点频)相比可得理论展宽倍数为：f/f≈1.423。可见理论计算值和实际仿真结果基本一致。将两个不同调制方式下的差频信号进行做傅里叶变换后的频谱如图4所示。

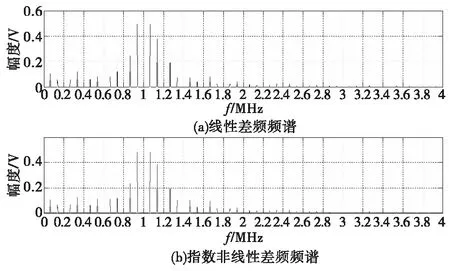
图4 40 MHz调制带宽时的差频频谱Fig.4 Spectrum of Difference frequency signal when B=40 MHz

当调频带宽为40 MHz，所对应的指数非线性度为L≈0.05时，式(15)与式(1)的差频频谱很接近，所对应的距离分辨率并没有降低。可见当调制带宽较小，指数非线性度不大于5%，使得回波频谱的展宽因子n<2时，本文所推建立调频引信指数型回波模型仿真计算结果与理想线性回波模型基本一致。

3.2 调制带宽B=150 MHz

实际工程应用时为了满足较高的距离分辨率指标而往往尽可能提高调频带宽，但此时采用RC电路的弊端就会显现出来。图5为大带宽条件下式(1)和式(16)描述的理想线性和指数非线性条件下的三角波调制频率波形。

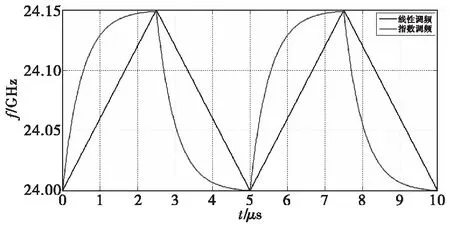
图5 150 MHz调制带宽时的发射频率曲线Fig.5 Transmitted frequency curve when B=150 MHz

可见此时指数频率调制的线性度已严重恶化，指数性变化规律较明显，由式(6)计算得L=47.17%。同样对上图中两条曲线分别与延时后的回波混频后可得差频频率曲线如图6所示。

由式(3)可计算得到此时对应10 m处的差频为4 MHz，指数差频在相比于40 MHz时的谱宽有很明显扩展，约为12.9 MHz。所对应谱线根数为n=12.9/0.2=64.5。将L=47.17%代入用式(18)后可得理论扩展倍数为：f/f≈59.3。考虑到不规则区和多普勒的影响，以上两值计算误差在允许范围之内，也就是说由于线性度的恶化将目标距离谐波谱展宽了至少10 MHz以上，其频谱对比情况可见图7。

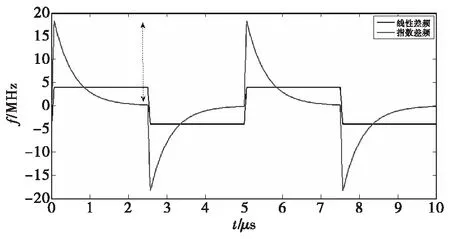
图6 150 MHz调制带宽时的差频频率曲线Fig.6 Difference frequency curve when B=150 MHz

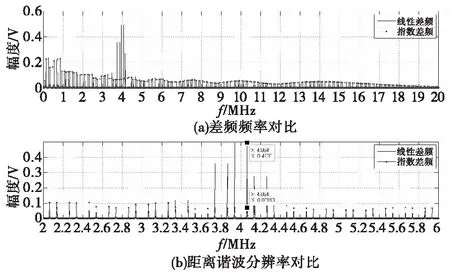
图7 150 MHz调制带宽时的差频频谱Fig.7 Spectrum of Difference frequency signal when B=150 MHz

相对比线性差频频谱，指数差频频谱已被大大展宽且能量也被分散，此时已经无法从谐波的包络能量分布明显区分出目标距离特征。由式(19)可计算出此时实际距离分辨率为R≈29.64 m，在带宽和线性度不变增加距离R=20 m时相应实际距离分辨率为R≈59.28 m。带宽不变，通过调整RC时常使线性度如图8所示进一步恶化时，差频频谱能量包络特征如图9所示。

经计算如图8(a)所示指数型非线性度已达到L=97.35%，由于充放电时常很小造成波形已非常接近周期性方波。由图9可以看到其频谱除频谱同样被展宽之外，其能量包络为sinc函数形式，即能量集中在直流和基波上。可见，因采用RC三角波发生电路使得调频引信信号的指数非线性度增加，频谱展宽因子n>2，此时调频引信系统的距离分辨率下降，不能再利用传统理想线性回波模型和距离分辨率计算方法进行系统设计与分析。

通过与理想线性回波模型的仿真对比发现：当使用RC三角波发生电路时，调频引信回波模型为指数非线性，当指数非线性度大于5%时实际回波频谱会展宽，造成距离分辨率相对于理想线性条件下恶化。

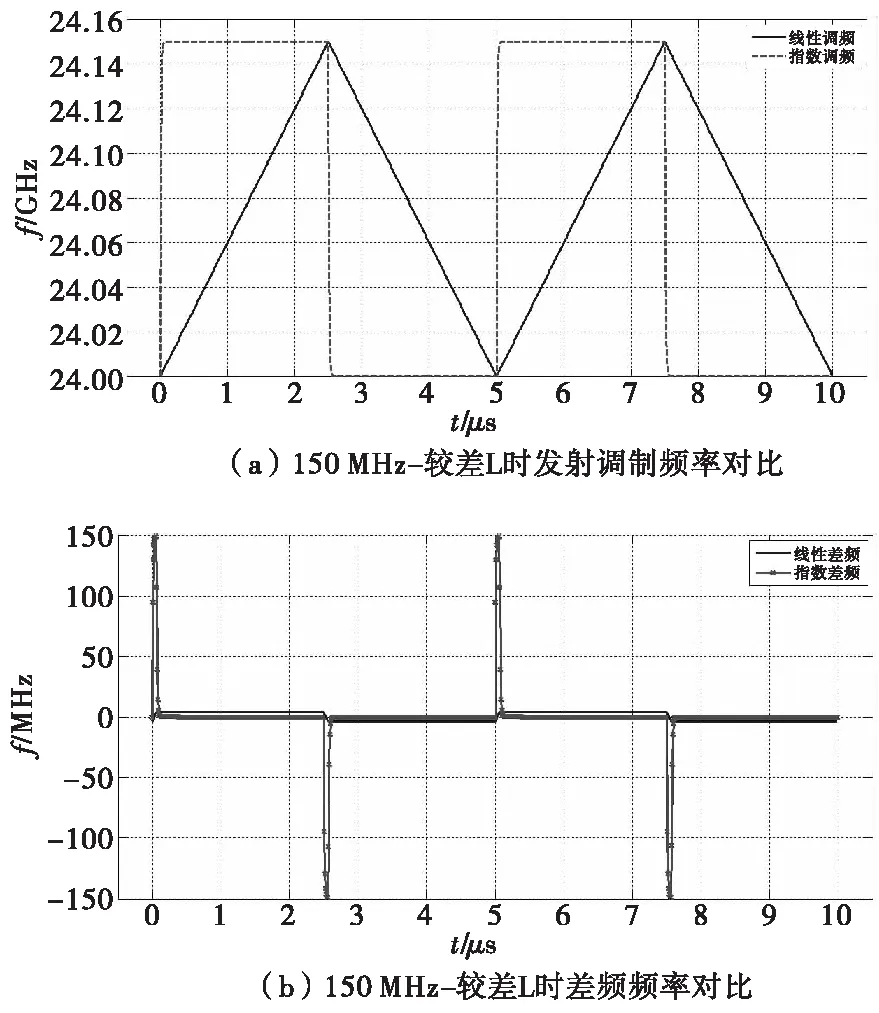
图8 L恶化后的频率对比Fig.8 Contrast of frequency when L is worsen

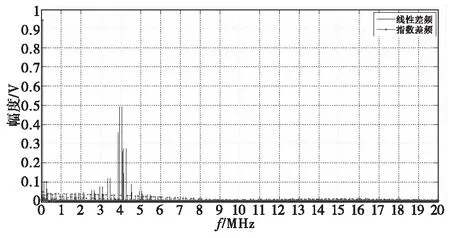
图9 L恶化后的差频频谱对比Fig.9 Contrast of Difference frequency signal spectrum when L is worsen

4 结论

本文提出了调频引信的指数型回波建模方法。该方法给出了周期性指数型三角波调制发射信号的频率分段解析式，对其在每个调制周期内进行定积分后归纳出连续性瞬时相位的一般解析式，该解析式与其相应延时信号作差拍处理后即可得到调频引信的指数型回波模型，在此基础上分析了指数非线性对距离分辨率的影响并给出了新的计算方法。仿真对比结果表明该模型有效，当指数非线性度大于5%时实际回波频谱会展宽，造成距离分辨率相对于理想线性条件下恶化。按照指数型回波模型进行仿真计算可以更准确地定量分析调频引信的回波频谱和距离分辨率。下一步应结合工程实践中的实测结果对比分析和验证指数非线性对调频引信距离分辨率的影响。