真空环境下高温气体静密封界面泄漏特性分析

白少先，李 栋，樊世超

（1. 浙江工业大学 机械工程学院，杭州 310032； 2. 北京卫星环境工程研究所，北京 100094）

0 引言

气体静密封作为基础部件的关键部位，在空间系统中的管路、阀门箱体中以金属垫圈、弹性垫片、O 形环等不同形式存在。在真空、高热、低温等空间环境条件下，密封的泄漏特性直接决定相关部件的使用寿命和可靠性。理论方面，气体静密封泄漏特性的设计和分析主要表现为气体接触润滑问题。1970 年，Greenwood 和Tripp[1]提出了解决接触问题的G-T 模型：假定粗糙峰形状为抛物线，以粗糙峰高度方均根偏差、轮廓峰曲率半径和轮廓峰密度描述表面粗糙度。G-T 模型更接近工程实际，奠定了接触问题的研究基础。1978 年，Patir 和Cheng[2-3]考虑微表面粗糙峰接触状况提出了平均流量模型，简称P-C 模型，其通过在雷诺方程中引入流量系数描述表面粗糙度的影响。基于P-C 模型和G-T 模型相结合建立的混合润滑模型，Hu 等[4]和Ruan 等[5]分别研究了活塞环的摩擦性能和机械密封性能。然而，这种混合润滑模型采用统计参数表征粗糙度，只能给出压力和膜厚的平均值，无法给出局部压力和膜厚变化的确切信息。因此，有研究基于对表面粗糙度进行确定性描述发展了确定性模型，其中应用比较成功的是Hu 和Zhu[6]提出的统一润滑模型。但是，现有接触模型的建立主要基于轴承的应用需求，考虑压力分布和载荷的修正，无法直接应用于密封界面微观流体运动，特别是泄漏率的准确计算分析。

空间密封面临更为严苛的高、低温使用环境，热效应对气体润滑密封的影响更突出。1959 年，Elrod 和Burgdorfer[7]进一步完善无限长气体轴承理论，从理论上说明了一般工况下润滑气膜内部的温升效应可以忽略。由此，等温假设在气体轴承的数值分析中被普遍接受，等温气体润滑理论被广泛应用于气体轴承和密封研究。然而，温度变化导致的表面热变形不仅影响泄漏率，同时影响密封气膜开启性能，是制约非接触气膜动密封可靠设计的重要因素[8-10]。目前，在气体动密封的热效应研究中，密封端面热变形对密封特性的影响成为分析重点[11-15]。1979 年，Gabriel[11]基于窄槽理论，近似求解螺旋槽端面气膜密封的热变形及压力分布情况，结果表明端面热变形会形成发散间隙，且转速、密封压力是影响密封端面温度场的主要因素。Thomas 等[12-13]对高压条件下楔形端面密封的研究表明，压力引起的端面发散变形导致密封气膜开启能力下降，而密封气体沿泄漏方向的体积膨胀、温度下降引起的端面热发散变形会进一步加剧这一下降趋势。相对而言，静密封要求更低的泄漏率，设计时除了要考虑密封结构导致的密封面宏观热、力变形外，密封介质在密封界面处的泄漏规律分析更为关键。

本文基于气体热流润滑理论，考虑表面粗糙度的接触问题和稀薄效应，建立真空环境下高温气体静密封混合润滑分析模型，对温度、表面粗糙度各因素对静密封界面泄漏的影响规律进行计算分析，以期为密封表面的粗糙度设计提供参考依据。

1 数学模型

工程实际中，通常在密封表面增加铜、金、银等软金属镀层以增强密封性。由于配副面的硬度差异较大，故可假设硬接触面粗糙度不发生塑性变形，并忽略软质表面粗糙度的影响。为使模型更具普遍性，采用如图1 所示的静密封单元结构，选择氮气为密封气体介质。

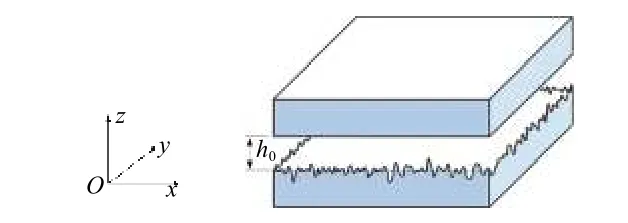
图 1 密封界面单元模型Fig. 1 Schematic view of seal interface unit

在密封压力作用下，气体沿x方向运动并产生泄漏。考虑表面粗糙度后，静密封界面实际处于非连续接触的气体混合润滑状态。当气膜厚度到达nm 量级，特别是小于分子平均自由程时，润滑气体的稀薄效应越来越显著。数值分析时采用气体Reynolds 方程[15]

式中：h为气膜厚度；ρ为气体密度；η为气体黏度；p为气体压力；Qp为考虑稀薄效应的流量修正系数，计算中采用Fukui 修正公式[16-17]

式中D=π0.5/(2Kn)，其中克努森数Kn=λ/h，分子平均 自 由 程λ=(η/2p)(2πRuT)0.5，理 想 气 体 常 数Ru=8.314 472 m3·Pa/(mol·K)。

根据Champman-Enskog 方程，可得到气体的黏度与温度的关系

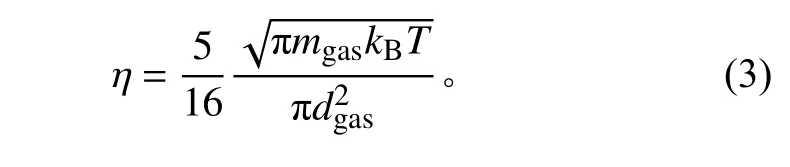
式中：kB为玻耳兹曼常数；mgas为气体分子平均质量；dgas为气体分子直径。对于氮气分子，mgas= 4.65×10-26kg，dgas= 3.64×10-10m。

不考虑气膜与固体间的传热，但考虑气体稀薄效应，则压力流润滑气膜的能量方程[15]为

式中cV是定容比热容。

气体温度方程[15]为

式中：id为气体分子运动自由度；Em为气体分子每个自由度对应的能量。

气体压力方程[15]为

式中cp为定压比热容，cp=Ru/cV。真空环境下，压力边界条件为：x=0 时，p=0。

可基于表面粗糙度参数Ra，利用随机函数模拟生成密封粗糙表面[18]。为分析表面粗糙度对静密封界面泄漏的影响，定义方向系数

式中，lx和ly分别为气膜在x和y方向上的相关长度。则，润滑区膜厚的分布表达式为

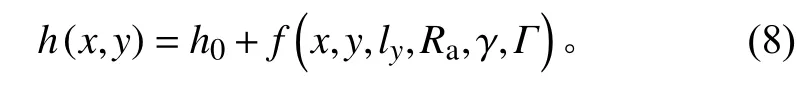
式中Γ为界面粗糙度分布形式。本文重点讨论高斯分布、泊松分布和指数分布这3 种形式。

以基础膜厚h0与表面粗糙度Ra的比值作为分析参数，定义为膜厚比

泄漏率的计算式为

为直观表征表面粗糙度对泄漏率的影响，定义流量系数Q，流量系数越小，泄漏率越低。

对于上述建立的数学模型，采用有限差分方法对Reynolds 方程、黏度方程、能量方程以及气体温度方程、压力方程进行耦合联立数值求解[15]，可得到密封润滑区气膜压力分布，进而得到泄漏率。

2 结果与讨论

图2 是高斯分布粗糙表面密封气膜间隙与压力分布：服从高斯分布的粗糙密封表面接触时产生如图2(b)所示的非连续密封间隙，对应形成如图2(c)所示的气体压力分布；在固体实际接触区域无气膜压力，意味着没有气体流动，无气体泄漏。

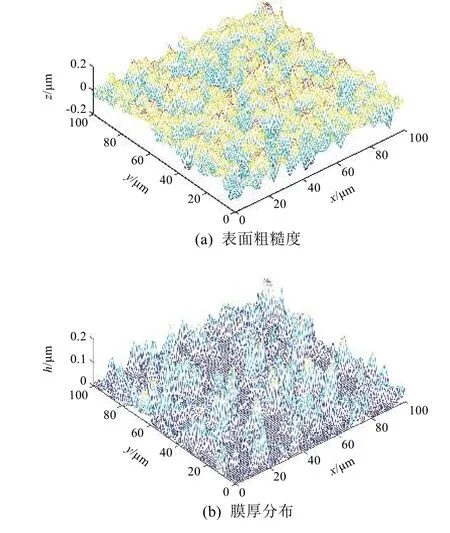
图 2 高斯分布粗糙表面密封气膜间隙与压力分布（Hs=200，Ra=0.2 μm，γ=1）Fig. 2 Distributions of gas film thickness and pressure of Gaussian rough surfaces

对于实际的密封面，由于粗糙度的存在，压力流引起的泄漏率不可避免地存在。下面分别对温度以及粗糙度的大小、方向、分布形式等因素对泄漏率的影响规律进行数值计算分析。计算中，润滑区面积为100 μm×100 μm，x方向相关长度取固定值lx=5 μm。

2.1 温度的影响

图3 是温度对流量系数Q的影响曲线。计算时，取Ra=0.2 μm，γ=1，粗糙度分布形式为高斯分布。从图中可以看出：温度越高，流量系数越小。计算时未考虑表面的热变形，即温度不引起膜厚分布的改变，因此随着温度的升高，气体温黏效应和稀薄效应整体上使得气体的泄漏率降低；在Hs=200的工况条件下，温度从200 K 升高到400 K 时，流量降低20%以上。同时可以看出，在同一温度条件下，膜厚比的增加，即膜厚的减小，使流量系数迅速增大，这意味着随着气膜厚度的减小，表面粗糙度形成的气体泄漏越发明显。

图 3 温度对流量系数的影响（Ra=0.2 μm，γ=1）Fig. 3 Influence of temperature on the flow factor

2.2 表面粗糙度大小的影响

图4 是表面粗糙度大小对流量系数Q的影响曲线。计算时，取T=300 K，γ=1，粗糙度分布形式为高斯分布。从图中可以看出：随着表面粗糙度的增大，流量系数显著增大，即在同等膜厚条件下，表面粗糙度越大流量越大；在Hs=200 的工况条件下，Ra=0.8 μm 密封表面的泄漏率是Ra=0.1 μm 表面泄漏率的10 倍以上。在工程实际中，表面粗糙度越大，同等预紧力条件下形成的气膜厚度越大，将导致更高的泄漏流量。因此，为获得良好的密封效果，要保证密封表面具有较小的表面粗糙度。

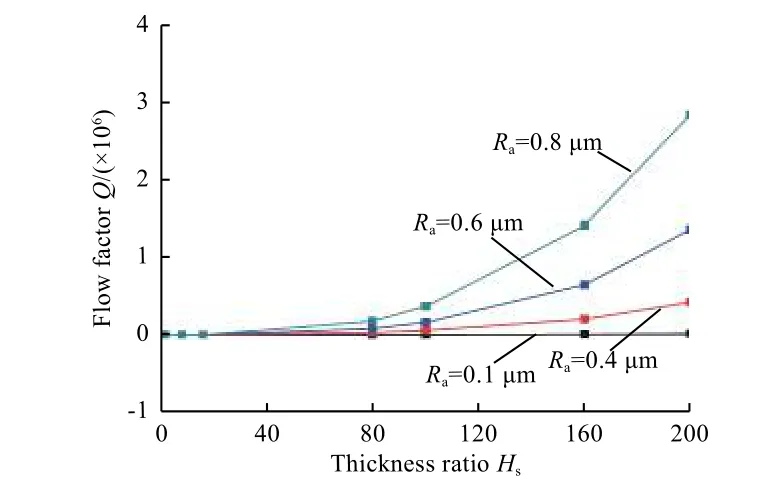
图 4 表面粗糙度对流量系数的影响（T=300 K，γ=1）Fig. 4 Influence of surface roughness on flow factor

为直观分析表面粗糙度大小对泄漏率的影响，对直径100 mm 的静密封进行数值计算分析，结果见表1。计算时，假设通过安装预紧密封面接触长度为1 mm，且密封基准面达到原子尺度的接触状态，即h0=1×10-10m。可以看出，表面粗糙度Ra由0.8 μm 降低到0.1 μm 时，泄漏率可降低约3 个数量级。

表 1 表面粗糙度大小对泄漏率的影响数值计算结果Table 1 Leakage rates on different rough surfaces

2.3 粗糙度方向的影响

图5 是粗糙度方向对流量系数Q的影响。计算时，取T=300 K，Ra=0.2 μm，粗糙度分布形式为高斯分布。从图中可以看出：γ＞1 表面的流量系数明显高于γ＜1 表面的，即粗糙度方向对密封性能有明显影响，是粗糙度效应中的重要影响因素；在Hs=200 的工况条件下，γ=5 表面的流量比γ=0.2 表面的高50%以上。其原因在于，随着方向系数的增大，沿x泄漏方向的流体阻力减小，导致流量增大；反之，随着方向系数的减小，沿x泄漏方向的流体阻力增大，导致流量减小。因此，在进行密封面研磨、抛光等处理时，可通过控制表面粗糙度纹理走向来降低泄漏率。

图 5 粗糙度方向对流量系数的影响（T=300 K，Ra=0.2 μm）Fig. 5 Influence of orientation of surface roughness on flow factor

2.4 粗糙度分布形式的影响

图6 是表面粗糙度分布形式对流量系数Q的影响。计算时，取T=300 K，Ra=0.2 μm。从图中可以看出：表面粗糙度分布形式对流量系数影响显著，3 种分布形式中，指数分布表面的泄漏率最大，其次是高斯分布表面，泊松分布表面的泄漏率最小；在Hs=150 的工况条件下，指数分布表面的流量系数是泊松分布表面的3 倍以上。粗糙度的分布形式主要与加工方式有关，因此，为了控制泄漏率，密封面的加工方式是不可忽略的影响因素。

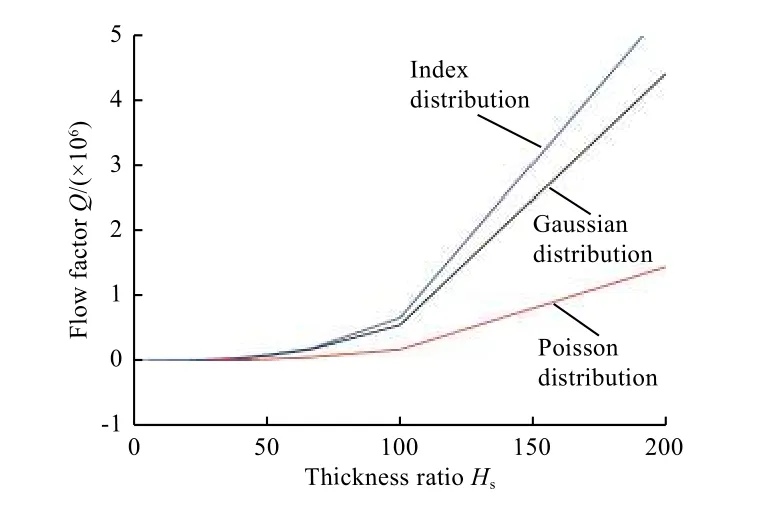
图 6 粗糙度分布形式对流量系数的影响（T=300 K，Ra=0.2 μm）Fig. 6 Influence of distribution type of surface roughness on flow factor

从以上分析可知，在真空、高温等特殊条件下，热效应对静密封泄漏的影响不可忽略；同时，泄漏率还受表面粗糙度大小、方向性和分布形式等多参数的显著影响，在实际工程表面设计、加工时，不仅要求表面粗糙度尽量小，同时要选择合适的加工方式和处理工艺。

3 结论

本文基于一定粗糙度的表面具有的非连续间隙分布特征，对真空环境下静密封的泄漏特性进行数学建模与仿真计算分析，主要结论如下：

1）真空低泄漏静密封设计时，气体热黏效应不可忽略。温度变化对气体静密封的泄漏率影响显著，气体热黏效应和稀薄效应综合作用下，泄漏率随温度的升高而降低——温度从200 K 升高到400 K时，泄漏率可降低20%以上。

2）表面粗糙度是影响气体静密封泄漏率的主要因素，粗糙度越小泄漏率越小，表面粗糙度由0.8 μm 减小到0.1 μm 时，泄漏率可降低约3 个数量级；同时表面粗糙度的方向和分布形式也是不可忽视的影响因素，低泄漏率静密封表面的工程实现依赖于表面粗糙度的合理设计和工艺实现。