倒挂结构的地震作用计算分析

卢伟煌

(福建省建筑设计研究院有限公司 福建福州 350001)

1 概述

倒挂结构在实际工程中常见，现有规范或规程《高层建筑混凝土结构技术规程》[1]《建筑抗震设计规范》[2]未涉及到地震作用如何计算问题；现有整体分析计算程序计算水平地震作用，未能反映倒挂结构质量上移的特点，从而使地震作用引起的效应偏小，结构属于不安全状态，未能满足建筑抗震设计规范对地震作用的要求。本文根据上述存在的问题，对各层重力荷载代表值(质量)的分布进行调整，重新计算各层水平地震作用，计算出调整前后各层水平地震作用的比值，对现有整体分析计算程序计算的各层水平地震作用进行调整，以满足结构的实际受力状态。

对现有的结构整体分析软件，每层重力质量不能根据吊杆的拉力进行上移重新分布，因此，只能通过人工干预，进行每层重力质量的重分布。

2 各层重力荷载代表值(质量)的调整

根据倒挂结构的竖向构件拉力对各层重力荷载代表值(质量)的分布进行调整，如图1所示。该示意图表示典型的倒挂结构及倒挂结构的竖向构件的受拉状态；现有整体分析计算程序，计算各层重力荷载代表值(质量)分布时，倒挂结构的竖向构件拉力未统计到各层重力荷载代表值(质量)中。

T1A，T2A…T6A和T1B，T2B…T6B是在“D+0.5L”工况下，每层吊杆的拉力；m1、m2、m3、m4、m5、m6、m7，是现有整体分析计算程序，计算的各层重力荷载代表值(质量)；F1、F2、F3、F4、F5、F6、F7，是现有整体分析计算程序，计算各层地震作用。

调整后各层重力荷载代表值(质量)为m01、m02、m03、m04、m05、m06、m07；

m01=m1-(T1A+T1B)

m02=m2-(T2A-T1A)-(T2B-T1B)

m03=m3-(T3A-T2A)-(T3B-T2B)

m04=m4-(T4A-T3A)-(T4B-T3B)

m05=m5-(T5A-T4A)-(T5B-T4B)

m06=m6-(T6A-T5A)-(T6B-T5B)

m07=m7+(T6A+T6B)

图1 倒挂结构的示意图

实际上现有整体分析计算程序，无法改变每层的重力荷载代表值(质量)；为了达到改变每层的重力荷载代表值(质量)目的，可以在每层的吊杆处施加向上(下)的力。

电算第1层楼面的吊杆处施加向上的力T1A、T1B；

电算第2层楼面的吊杆处施加向上的力T2A-T1A、T2B-T1B；

电算第3层楼面的吊杆处施加向上的力T3A-T2A、T3B-T2B；

电算第4层楼面的吊杆处施加向上的力T4A-T3A、T4B-T3B；

电算第5层楼面的吊杆处施加向上的力T5A-T4A、T5B-T4B；

电算第6层楼面的吊杆处施加向上的力T6A-T5A、T6B-T5B；

电算第7层楼面的吊杆处施加向下的力T6A、T6B。

3 计算调整各层重力荷载代表值(质量)后的地震作用

虽然通过各层重力荷载代表值(质量)的调整，结构的总质量不会改变，重新按现有整体分析计算程序计算各层地震作用，每层的地震作用为F01、F02、F03、F04、F05、F06、F07；计算出调整前后的各层水平地震作用的比值：K1=F01/F1，K2=F02/F2，K3=F03/F3，K4=F04/F4，K1=F05/F5，K6=F06/F6，K7=F07/F7。

用各层重力荷载代表值(质量)调整前的结构计算模型，引入各层地震作用的比值，重新计算结构内力，该计算结果即为最终的计算结果。

4 算例分析

本算例结构平面布置图如图2所示，剖面图如图3所示，地面以上7层，一层层高10m，二至六层层高4.5m，七层层高5m；屋面设置大梁，通过吊杆把下面6层的部分荷载传到屋面大梁，属倒挂结构；抗震设防烈度7度(0.10g)，设计地震分组第三组，建筑场地类别三类，建筑抗震设防类别丙类，结构的阻尼比5%，使用的分析程序YJK。

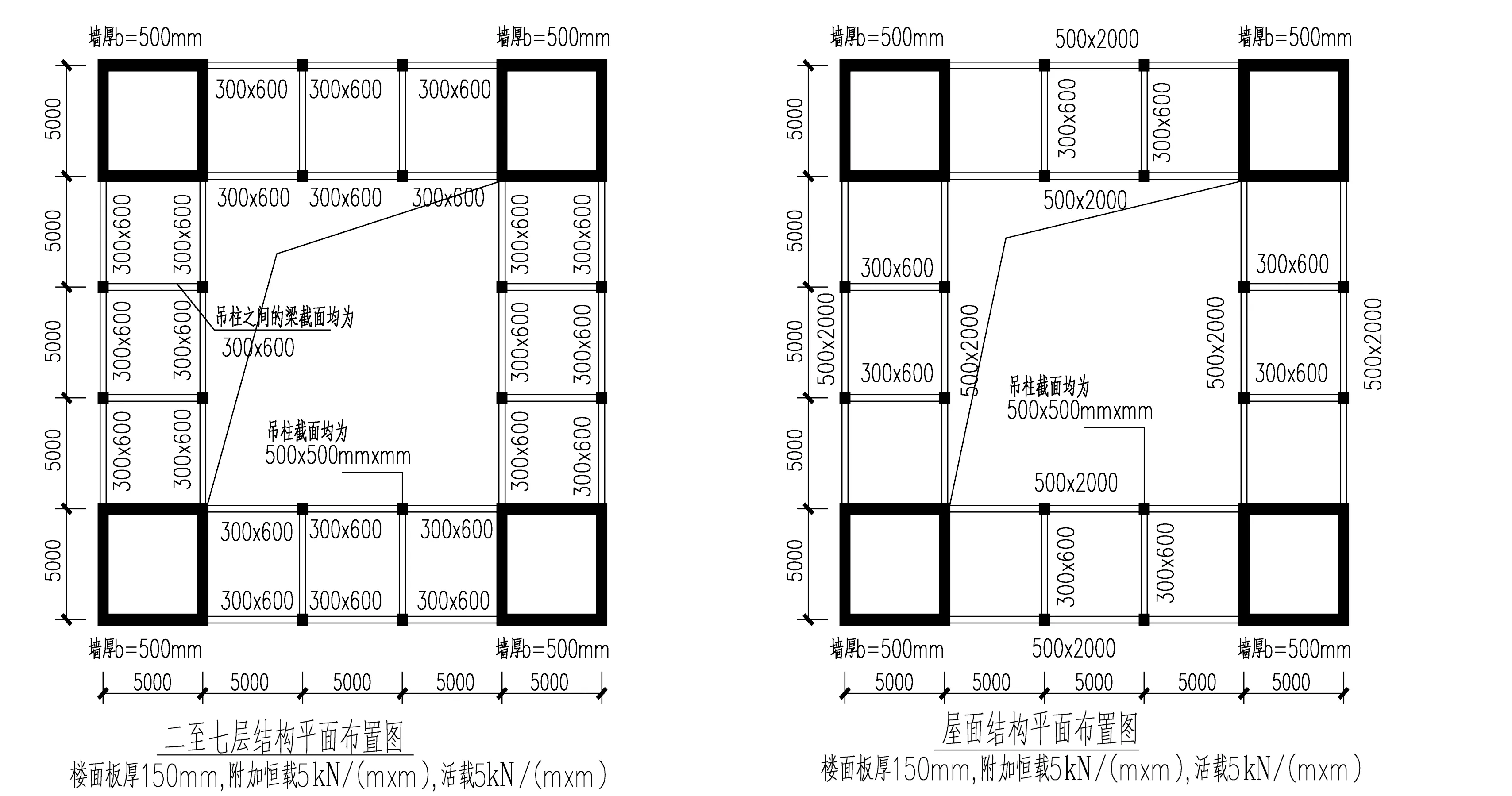
图2 算例的结构各层平面布置图

图3 算例的结构剖面图

按现有上部结构分析程序YJK计算结果如表1所示(由于X、Y方向完全对称，仅列出一个方向的计算结果)。

该平面每层面积： 每层活载质量2000kN，从表1可看出，该上部结构分析程序YJK，未作上吊质量的提升。

共有44根吊柱，每根吊柱的拉力如下：二层每根吊柱拉力T2=81.1kN(40.6kN)，三层每根吊柱拉力T3=182.35kN(77.65kN)，四层每根吊柱拉力T4=290.4kN(116.7kN)，五层每根吊柱拉力T5=403.25kN(157.2kN)，六层每根吊柱拉力T6=526.8kN(201.15kN)，七层每根吊柱拉力T7=616.8kN(234.45kN)。

通过人为干预各层质量分布后，按现有上部结构分析程序YJK计算结果如表2～表6所示(由于X、Y方向完全对称，仅列出一个方向的计算结果)。

表1 各层的质心、质量

表2 考虑扭转藕联时的振动周期(秒)、平动系数、扭转系数

表3 各层的地震力Fx(kN)、各层的剪力Vx(kN)，各层地震力作用下的弯矩M(kN-M)

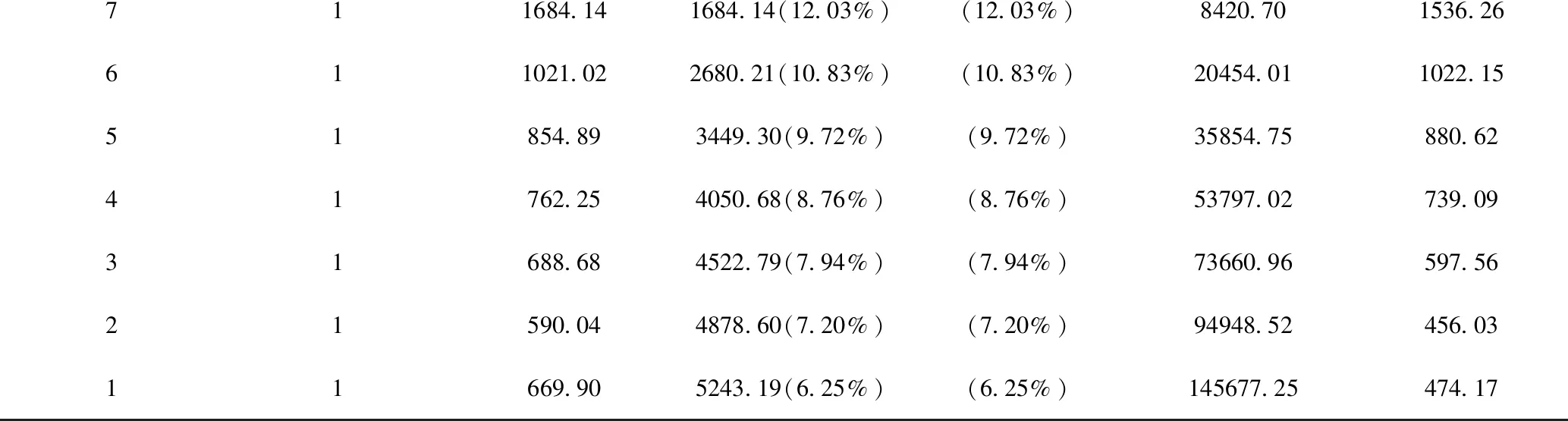
711684.141684.14(12.03%)(12.03%)8420.701536.26611021.022680.21(10.83%)(10.83%)20454.011022.1551854.893449.30(9.72%)(9.72%)35854.75880.6241762.254050.68(8.76%)(8.76%)53797.02739.0931688.684522.79(7.94%)(7.94%)73660.96597.5621590.044878.60(7.20%)(7.20%)94948.52456.0311669.905243.19(6.25%)(6.25%)145677.25474.17

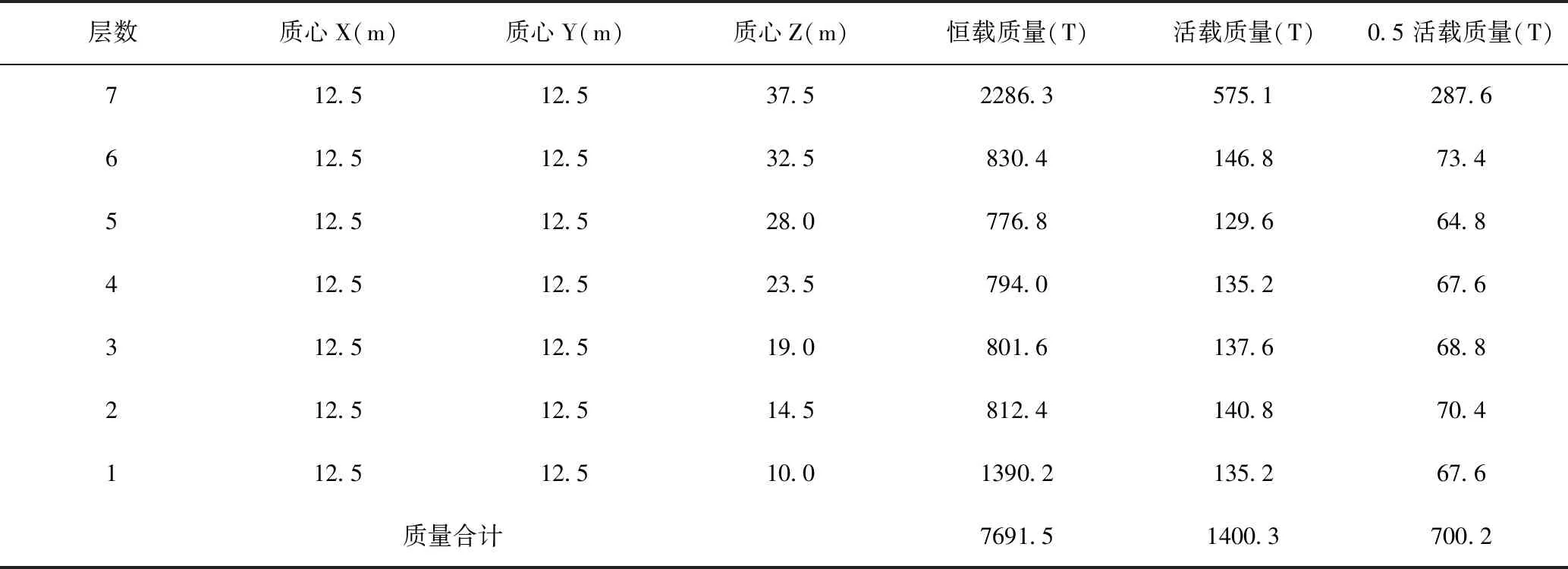
表4 各层的质心、质量

表5 考虑扭转藕联时的振动周期(s)、平动系数、扭转系数

表6 各层的地震力Fx(kN)、各层的剪力Vx(kN)，各层地震力作用下的弯矩M(kN-M)

通过人为干预各层质量分布后，与干预前的基底的地震剪力比5292.61/5247.35=1.008，地震做用下基底弯矩比160 545.65/145 851.41=1.1007。

每层地震力调整系数如表7所示：

表7 每层地震力调整系数

因此，把质量上移的影响，可通过每层地震力调整系数Ki来考虑。通过调整系数，对未经调整的结构整体分析模型进行各层地震作用的调整，就可以计算出基底剪力和基底弯矩。

5 结论

通过上文的算例分析，现有整体分析计算程序无法对倒挂结构按实际情况进行地震作用的分析，主要原因是目前的整体分析计算程序，统计每层重力荷载代表值(质量)时，无法减去被吊杆“吊走”的质量或增加被吊杆“下拉”的质量，造成计算地震作用错误。由于倒挂结构质量上移，地震作用引起的效应增大，因此对倒挂结构的工程，必须进行各层质量的调整，否则结构处于不安全状态，不能满足建筑抗震设计规范对地震作用的要求。

该工程算例，由于层数不多，基底剪力增加的不多，基底弯矩仅增加10%左右，但随着层数的增加，上吊的重力质量越高，其重心也越高，基底剪力和基底弯矩也会随着增加的更明显。因此对这种倒挂结构地震力计算与常规结构有一定的区别。

在这里需要说明的是，对于倒挂结构的地震力计算，有一定的争议，主要观点是质量是不会上移，质量在那个标高，其地震作用也在那个标高。本文目的是引起科研和设计人员注意，对于倒挂结构地震力计算的问题，欢迎大家探讨。