爆破荷载作用下隧道中隔岩稳定性研究

吴 波，兰扬斌，吴昱芳，杨仕升，路 明

(1.广西大学 土木建筑工程学院，广西 南宁 530004；2.广西大学 工程防灾与结构安全教育部重点实验室，广西 南宁 530004)

0 引言

近年来，随着国民经济的发展，我国交通隧道的建设也迅速发展起来，铁路隧道、公路隧道、地下铁道、水底隧道的建设里程不断增加。在修建交通隧道的过程中，越来越多的施工难题会持续出现，特别是在房屋密集、交通繁忙的城市中修建地下隧道，对施工安全控制十分严格。当隧道开挖过程中需要较硬岩石时，还需采用钻爆法开挖手段，在爆破冲击荷载作用下，隧道围岩稳定性会受到极大的影响，严重时甚至会出现隧道坍塌和地面塌陷，进而使城市交通陷入困境。因此，隧道围岩的稳定性问题已引起众多工程界专家学者的广泛关注。

目前，关于隧道稳定性的研究工作主要集中在静力开挖阶段，采用的研究手段多为数值模拟法、可靠度分析法、物理模型法、现场监测法。胡亚峰等[1]通过有限元模拟研究了浅埋隧道失稳的原因和主要影响因素，定性分析了上下台阶掌子面最容易失稳的部位；李典庆等[2]通过结合极限平衡法和有限元法，提出了边坡协同式可靠度分析方法，并表示该法的计算效率优于传统的蒙特卡罗模拟方法；Sterpi等[3]通过物理模型试验，以铝棒为相似材料，采用气囊逐步卸压的方法模拟隧道的开挖，对单洞和小净距双洞浅埋隧道的稳定性进行了平面应变研究；徐华等[4]通过开展大型三维振动台模型试验，研究了隧道结构的地震动力响应规律及隧道与围岩的相互动力作用，并提出隧道结构的加速度响应大于周边围岩且对周边岩土体的加速度响应有一定的放大效应；张平等[5]通过现场监测和数值模拟分析了不同煤层厚度条件下隧道爆破引起的围岩振动特性，并提出隧道拱顶位置处存在的安全隐患最大；郑颖人等[6]首次将强度折减法应用于隧道工程中，以整体安全系数定量分析隧道的安全性。上述学者对隧道稳定性和安全性进行了大量的研究，并取得了丰富的研究成果，但是对于城市小净距隧道爆破中隔岩稳定性评价标准研究甚少。

本文结合强度折减动力分析法和数值模拟呈现了隧道中隔岩在爆破荷载作用下塑性区的演变过程，以及塑性区贯通时后行洞隧道特征点位移的变化情况，并与规范中规定的位移限值作对比分析。由此对小净距隧道爆破中隔岩的稳定性进行评价。

1 强度折减动力分析法

1.1 强度折减动力分析法屈服准则

强度折减动力分析法是1种基于岩土体材料张拉-剪切复合屈服准则的有限元强度折减法，主要适用于岩土体承受动力荷载作用下的稳定性分析。对任一方位平面来说，设σn为该平面上的正应力，当此正应力等于岩土材料的抗拉强度时，岩土体会发生张拉脆性破坏，破裂面平行于张拉作用屈服面，张拉屈服准则表示为：

Ft=σn-σt=0

(1)

式中：Ft为剪切屈服准则；σn为方位平面上的正应力，MPa；σt为抗拉强度，MPa。结合M-C材料张拉-剪切复合屈服准则，任一方位平面上，岩土材料的张拉-剪切复合屈服准则即为：

Fs=|τ|+σntanφ-c

(2)

式中：Fs为剪切屈服准则；τ为抗剪强度，MPa；c为围岩的黏聚力，MPa；φ为摩擦角，(°)。

1.2 强度折减动力分析法的原理

通常，强度折减法在静力作用下只需考虑将围岩的抗剪强度指标黏聚力c和摩擦角的正切值tanφ分别折减ω，使围岩达到极限平衡状态，此时围岩的折减系数即为安全系数[7]。由文献[8]可知，隧道围岩在爆破动力荷载作用下，岩体的破坏是受拉、剪复合破坏作用的结果。因此在分析动力作用下围岩稳定性的问题中，应考虑岩体的张拉破坏，这样更加符合岩体的破坏本质。因此在进行强度折减同时考虑抗剪强度和抗拉强度的折减。根据文献[9]可知，在冲击荷载作用下岩体的内摩擦角和黏聚力都有明显提高，但具体的提升修正系数未知。为了使所求的安全系数偏保守，在动荷载下所选岩体抗压、抗拉强度与静载条件下相同。

1.3 动力安全系数计算及失稳判据

在计算爆破开挖隧道中隔岩安全系数时，首先按式(3)将围岩强度参数黏聚力c、抗拉强度σt和内摩擦角的正切值tanφ同时除以1个系数ω得到1组新的c′，σt′，φ′值[10]，然后作为新的材料参数输入，再进行试算；直到中隔岩塑性区贯通或隧道洞周位移超过规范值，此时的折减系数即可认为是隧道整体安全系数。

(3)

式中：ω为折减系数；c为围岩黏聚力，MPa；σt为围岩抗拉强度，MPa；φ为围岩的内摩擦角，(°)；c′为折减后围岩黏聚力，MPa；σt′为折减后围岩抗拉强度，MPa；φ′为折减后围岩内摩擦角，(°)。

目前，有限元数值计算中对于常规岩土工程失稳判据主要有塑性区贯通、特征点位移突变、计算不收敛3种[11]。但在小净距隧道中，由于中隔岩是极其脆弱的部位，最容易发生破坏，因此中隔岩塑性区贯通即可认为隧道发生失稳破坏[12]；由于隧道围岩整体稳定性计算时难以做到边坡工程中的全局搜索，因此本文以隧道围岩位移值是否超过规范和中隔岩塑性区是否贯通共同作为围岩位移失稳判据。

2 数值模拟

2.1 数值模型

结合强度折减动力分析法和FLAC3D模拟软件对福州地铁2号线洋里站矿山法段隧道中隔岩的稳定性进行数值计算分析。采用三维数值模型，其中x轴指向隧道开挖方向的右侧，y轴指向隧道开挖方向，z轴竖直向上。实际中左右线隧道净距为1.6～3.5 m，本文计算所选的模型净距分别为1.6，2.5，3.0，3.5 m。2隧道截面最大宽度均为7.8 m，上台阶高度均为4.56 m，下台阶高度为3.87 m，隧道埋深为9 m，模型正截面的中心点为隧道中隔岩柱中点。考虑到隧道对周围围岩扰动的影响范围为3～5倍隧道洞径，因此取岩土体区域为80 m×48 m×72 m，隧道模型正面如图1所示。将模型的4个侧面和底部均设置为无反射的黏性边界，地表及隧道已开挖区周边设为自由边界。

2.2 爆破荷载

根据文献[13]，爆破荷载可简化为具有线性上升段和下降段的三角形荷载，上升段时间tr和总作用时间ts计算公式分别为：

(4)

式中：K为岩体的体积弹性模量，105Pa；v为岩体的泊松比；r为对比距离。爆破荷载Pmax(kPa)采用经验公式(5)求解：

(5)

式中：Z=R/Q1/3为比例距离；R为爆心至荷载作用面的距离，m；Q为炸药量，kg，齐发爆破时取总装药量，分段起爆时取最大装药量。根据文献[14]可设置峰值压力的升压时间为100 ms，卸载时间为500 ms，总计时间取1 s。

2.3 计算参数

根据福州地铁2号线洋里站隧道段初步设计所提供的地勘资料得知，该隧道段多分布为中风化和微风化岩，且围岩等级主要为Ⅳ，Ⅴ级围岩，需要进行爆破开挖。围岩在冲击动荷载作用下，力学参数会发生变化，因此在数值模拟中需要选取岩石的动力学弹性模量和泊松比。目前许多学者对基于静力学参数的动力学参数的取值确定进行了详细的研究，单钰铭等[15]对岩石的动静力学参数提出了转化公式：

(6)

式中：Ed为岩石动弹性模量，GPa；Es为岩石的静弹性模量，GPa；μd为岩石动泊松比；μs为岩石静泊松比。围岩的具体力学参数见表1。

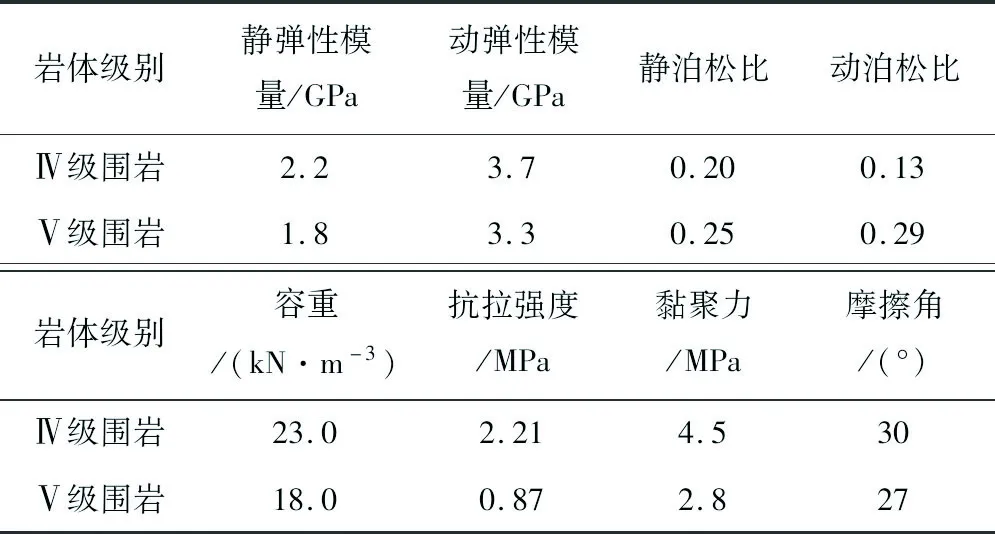
表1 围岩力学参数Table 1 Mechanical parameters of surrounding rock

3 结果分析

由于现场先行洞和后行洞掌子面错开距离为10 m，但隧道净距在1.6～3.5 m范围内变化，且隧道开挖进尺也会发生变化，通过控制变量法模拟隧道在不同净距、不同开挖进尺下的安全系数变化情况。参考《公路隧道施工技术规范》隧道周边允许相对位移见表2。

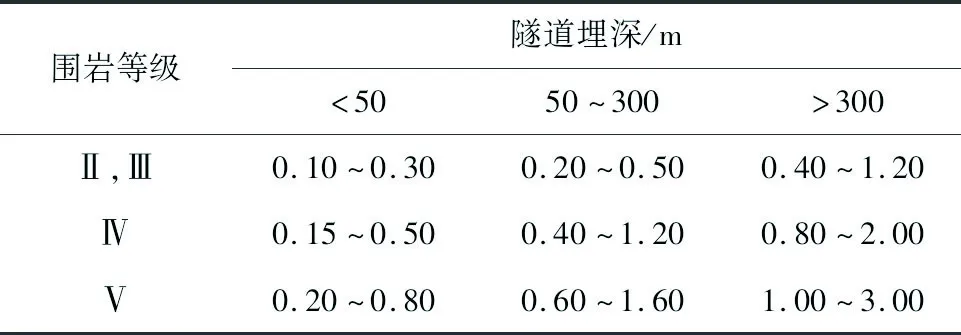
表2 隧道周边允许相对位移Table 2 Permissible relative displacement around tunnel %

注：相对位移是指实测位移值与2点间距离之比，或者是拱顶下沉实测值与隧道宽度之比。

由于计算过程中没有出现不收敛的情况，因此数值计算主要考虑中隔岩塑性区贯通、位移超过规范值这2种判据。本次计算选取最不利Ⅴ级围岩，并假定单位进尺药量保持不变。由于左右洞隧道宽度均为7.8 m，且隧道埋深为9 m。根据《锚杆喷射混凝土技术规范》中对隧道整体稳定允许相对位移的界定[16]可计算得到隧道周边允许相对位移值为1.56～6.24 mm。

3.1 不同净距隧道中隔岩安全系数计算

3.1.1 塑性区分析

由于隧道净距范围为1.6～3.5 m，为了研究隧道净距变化对隧道围岩及中隔岩安全系数的影响，选取净距为1.6，2.5，3.0，3.5 m的Ⅴ级围岩隧道计算模型，爆破方式均采用上台阶爆破，开挖进尺均为2 m。隧道不同净距围岩塑性区分布如图2所示，且隧道中隔岩贯通时的折减系数分别为2.07，2.16，2.24，2.34。中隔岩塑性区贯通参数值见表3。

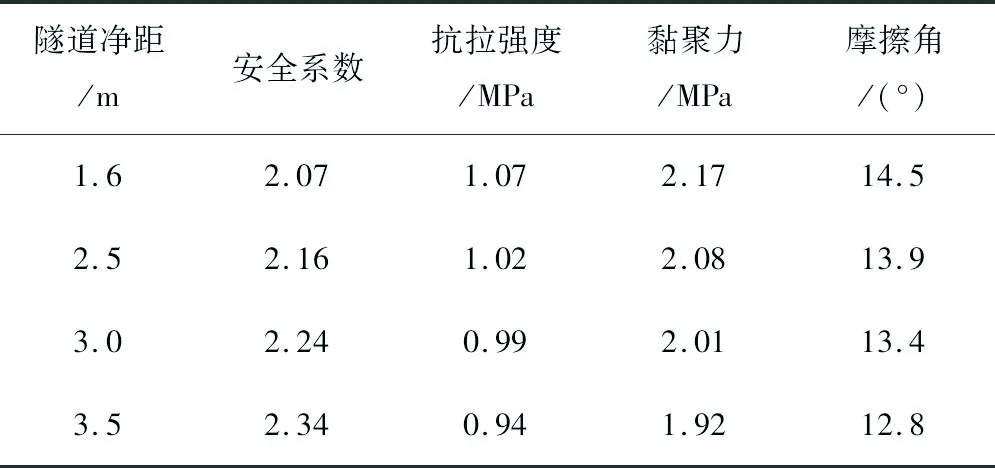
隧道净距/m安全系数抗拉强度/MPa黏聚力/MPa摩擦角/(°)1.62.071.072.1714.52.52.161.022.0813.93.02.240.992.0113.43.52.340.941.9212.8

3.1.2 位移分析

通过观察图2可知，左洞上台阶爆破开挖时，左洞拱顶塑性区面积较大，同时后行洞拱肩处塑性区贯通最快，由此可判定左洞拱顶和拱肩为隧道爆破开挖时的最危险位置，并选取各部位的特征点来进行重点分析，特征点位置如图3所示。不同净距隧道情况下中隔岩贯通时的特征点位移值见表4，其中AZ，BZ，CX分别代表左洞拱顶的竖向位移、拱肩的竖向位移、拱腰的水平位移。其中，净距为1.6，2.5 m特征点的位移时程曲线如图4～5 所示。

通过分析图4～5和表4发现，隧道的整体安全系数与隧道净距成正比，净距越大，隧道整体越安全；隧道净距为1.6 m时，只有左洞拱肩竖向位移为6.71 mm，超过了隧道周边允许相对位移6.24 mm，其他均在安全范围之内，因此隧道净距不宜小于1.6 m。

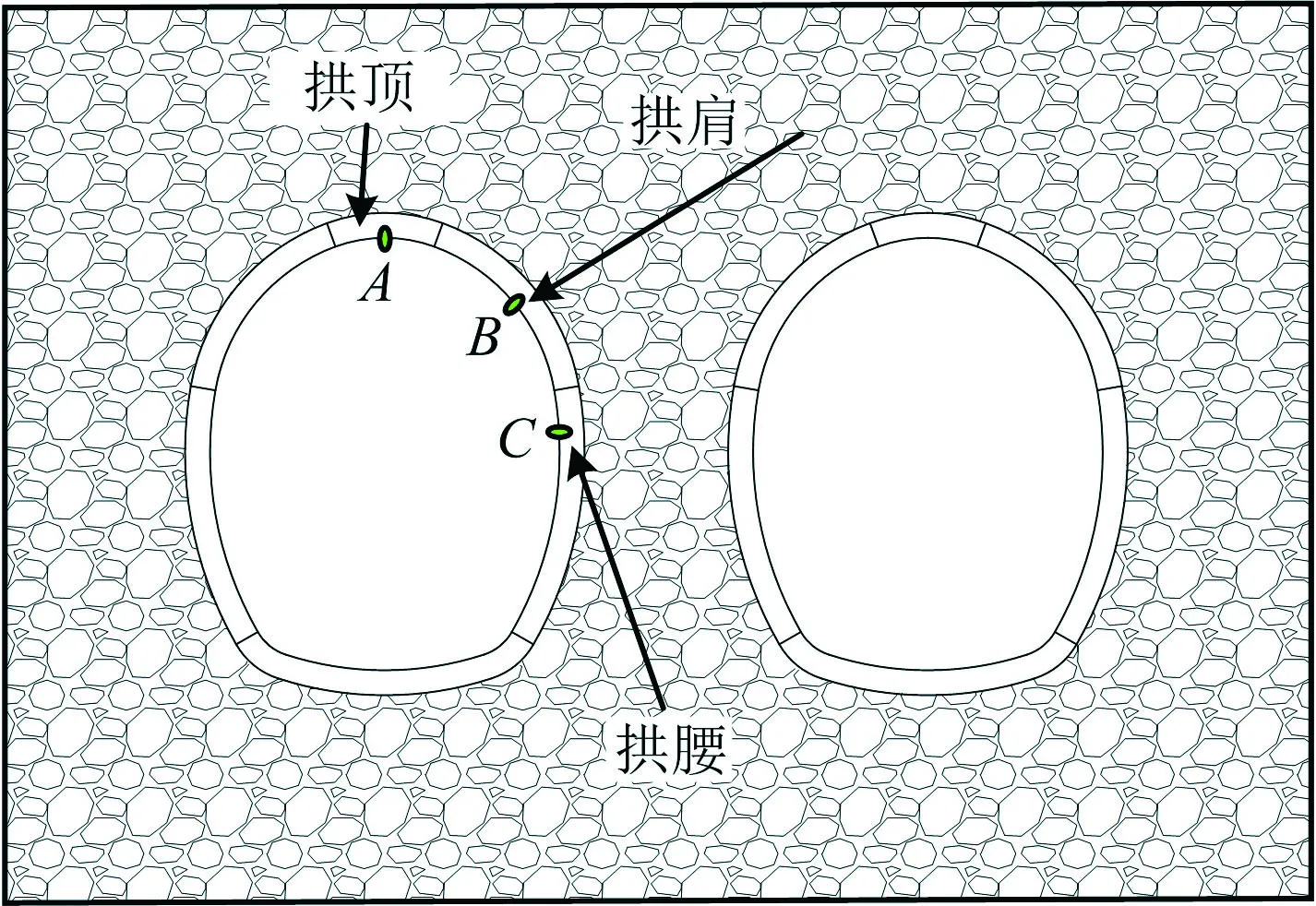
图3 特征点位置Fig.3 Location of characteristic points

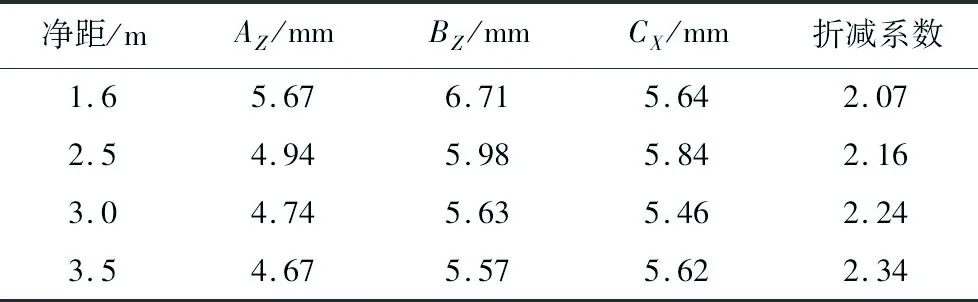
净距/mAZ/mmBZ/mmCX/mm折减系数1.65.676.715.642.072.54.945.985.842.163.04.745.635.462.243.54.675.575.622.34

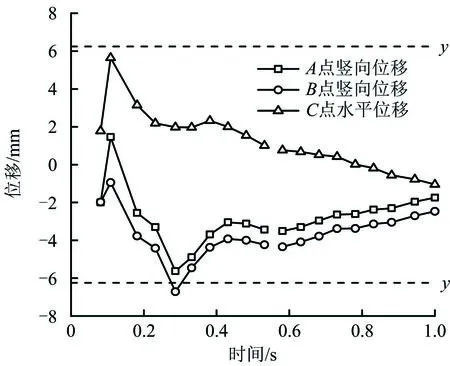
图4 净距为1.6 m特征点位移时程Fig.4 Time-history of displacement at characteristic points under net distance of 1.6 m

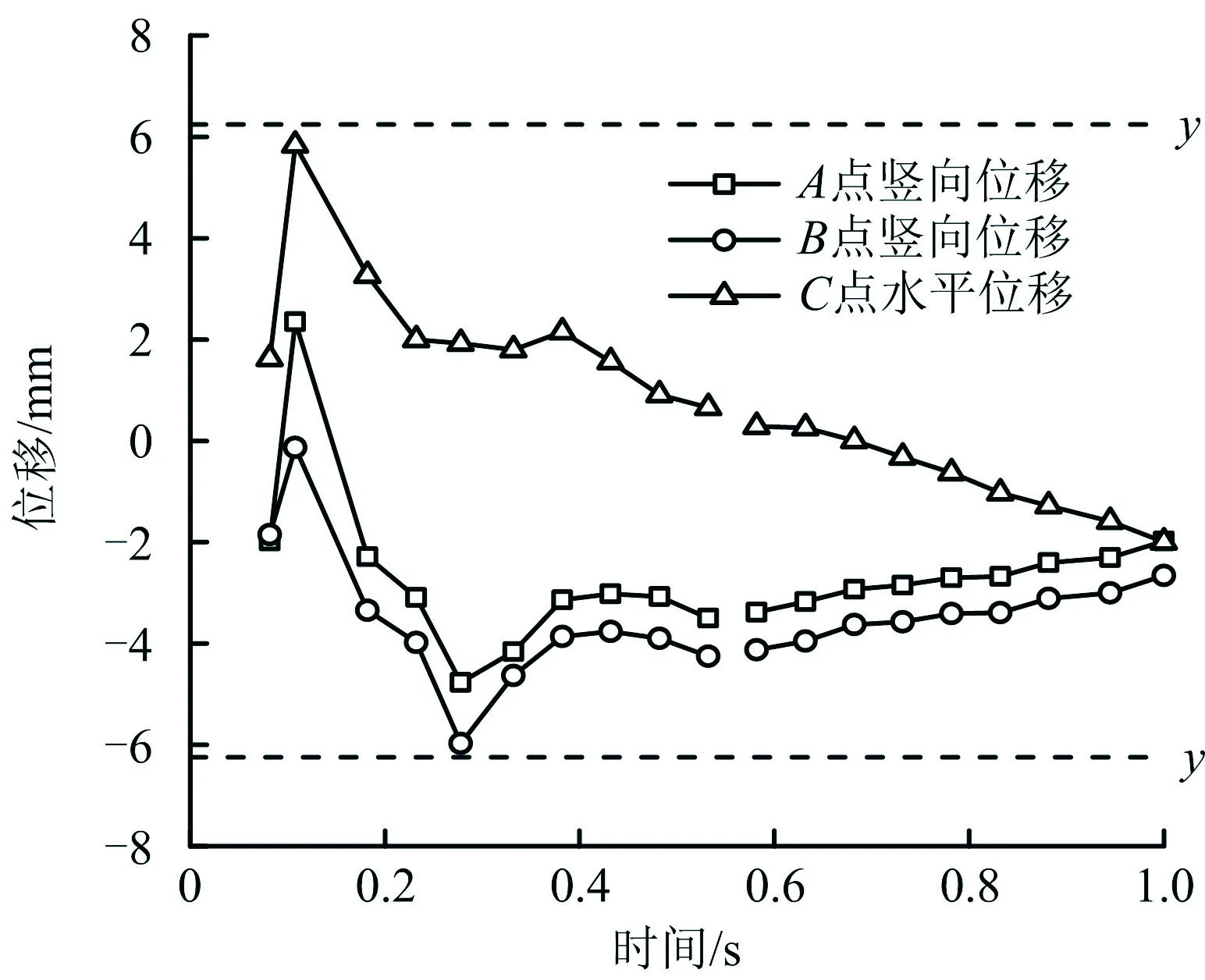
图5 净距为2.5 m特征点位移时程Fig.5 Time-history of displacement at characteristic points under net distance of 2.5 m

3.2 不同进尺隧道中隔岩安全系数计算

3.2.1 塑性区分析

选取Ⅴ级围岩，开挖方式选用上台阶爆破开挖，分析不同开挖进尺对隧道围岩及中隔岩安全系数的影响。开挖进尺分别为2，3，4，5 m隧道中隔岩塑性区贯通时所对应的塑性区分布情况如图6所示，贯通时对应的折减系数分别为2.07，1.55，1.34，1.21。不同进尺中隔岩贯通时围岩参数如见表5。

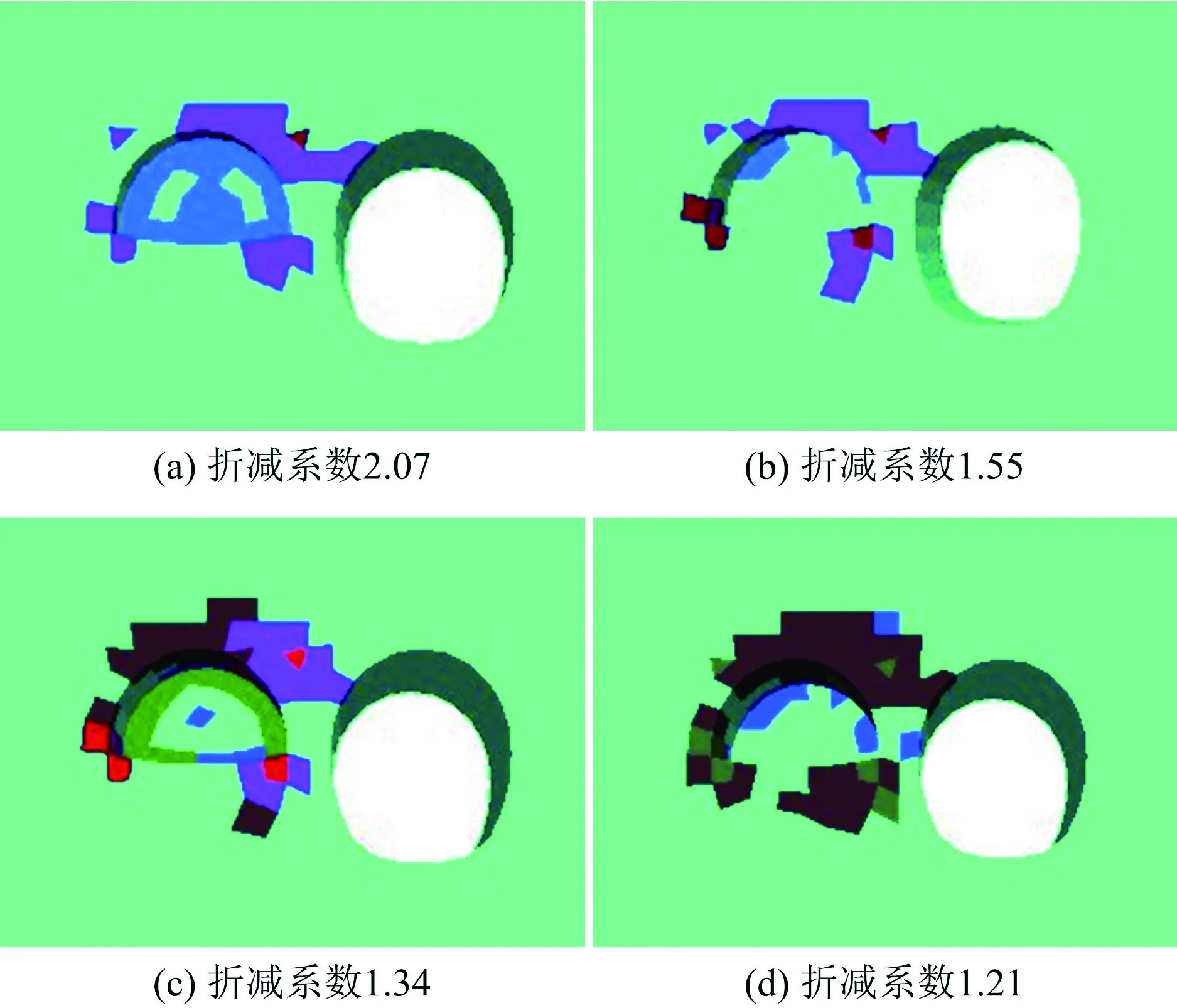
图6 不同进尺围岩塑性区分布Fig.6 Distribution of plastic zone in surrounding rock under different footages

3.2.2 位移分析

观察图6可知，隧道中隔岩最先在拱肩处贯通，且拱顶处塑性区面积较大，因此重点关注拱顶和拱肩处位移。不同进尺中隔岩贯通时围岩参数见表6。开挖进尺为3，4 m时特征点位移时程曲线如图7～8所示。

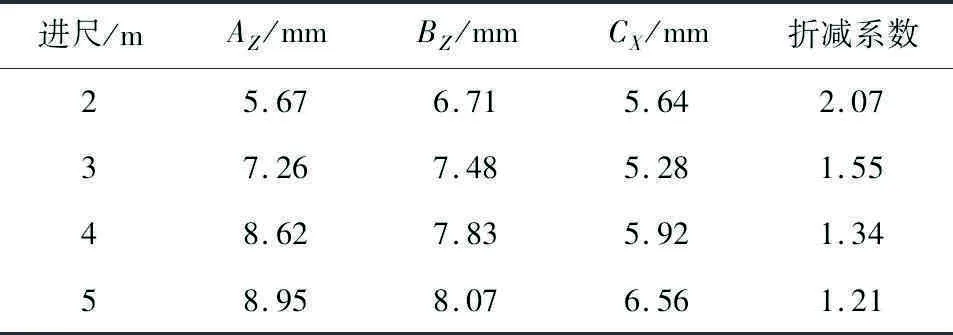
表6 不同进尺中隔岩贯通特征点位移Table 6 Displacement of characteristic points when intermediate diaphragm rock penetrating under different footages

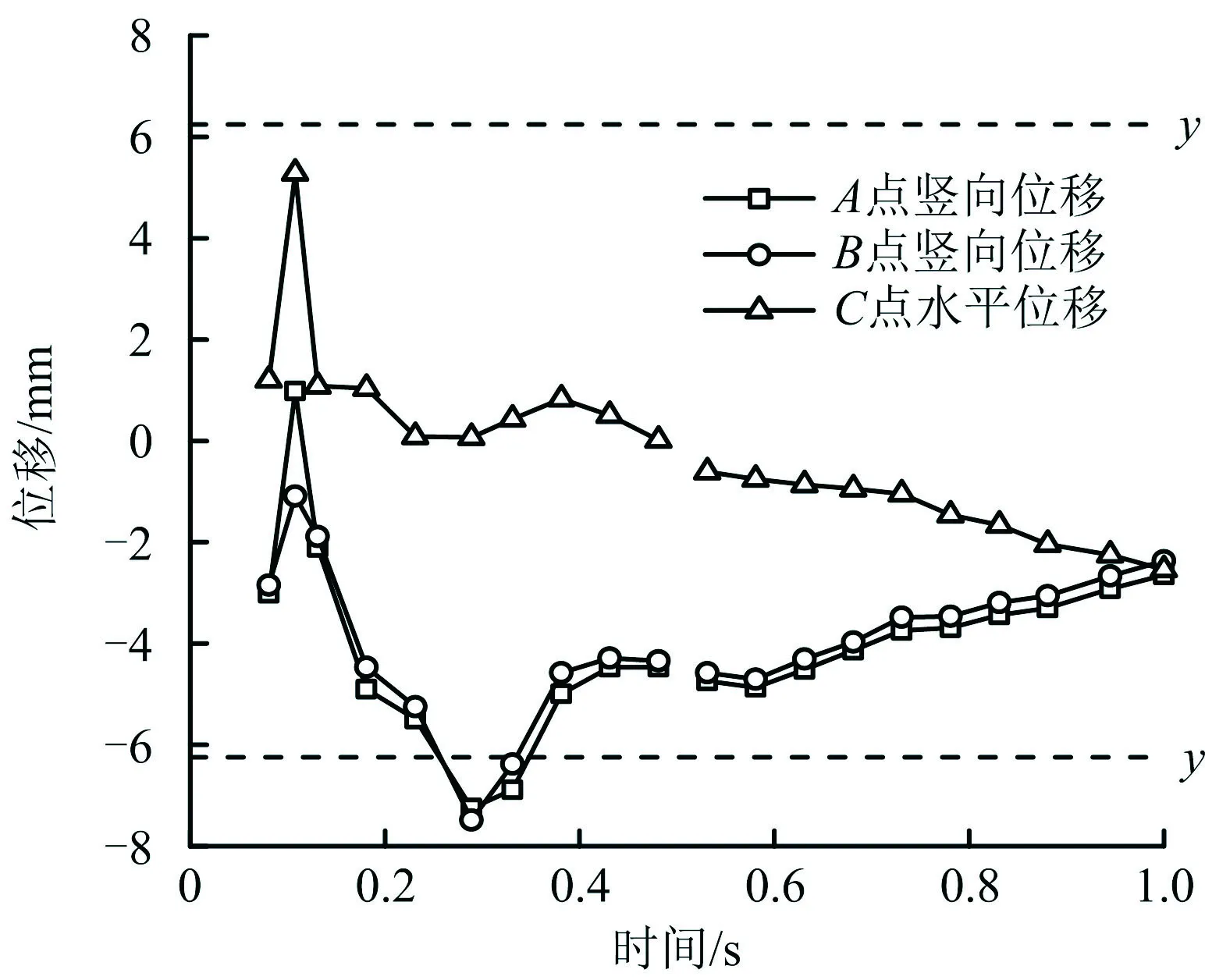
图7 进尺3 m特征点位移时程Fig.7 Time-history of displacement at characteristic points under footage of 3 m

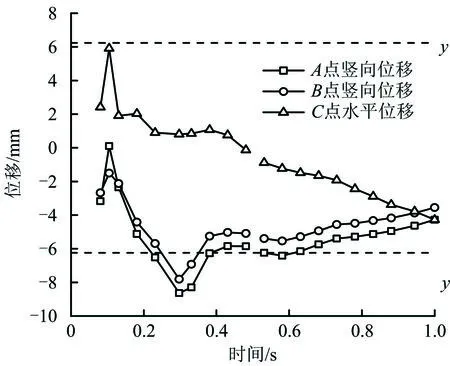
图8 进尺4 m特征点位移时程Fig.8 Time-history of displacement at characteristic points under footage of 4 m

通过分析表6和图7～8可知，开挖进尺越大，折减系数越小，隧道整体越不安全；当开挖进尺为5 m时，安全系数值为1.21 m，小于安全系数规定界限值，故在Ⅴ级围岩条件下不宜采用5 m开挖进尺；另外，进尺3，4，5 m时左洞隧道拱顶和拱肩处竖向位移均超过允许相对位移值，因此建议在围岩条件较差的情况下开挖进尺控制在2 m左右。

4 结论

1)通过对小净距中隔岩塑性区发展过程的分析，发现受爆后行洞隧道拱肩处围岩最先发生剪切破坏，为最薄弱的位置；随着折减系数的递增，受爆隧道拱肩处的塑性区逐渐向邻洞扩展，直至贯通中隔岩。

2)隧道中隔岩塑性区贯通时后行洞隧道特征点位移和规范中位移限值较为接近，可共同作为评价中隔岩稳定性的最终评价标准。

3)通过对隧道不同净距、不同开挖进尺下隧道整体安全系数的计算，发现净距越大、开挖进尺越小，安全系数越大。建议若隧道净距在1.6 m左右时，应采用上台阶爆破的方式，且开挖进尺需控制在2 m以内。