分数Maxwell黏弹性胶体阻尼缓冲器启动流模型

王之千，毛保全，冯帅，杨雨迎，朱锐

(陆军装甲兵学院 兵器与控制系, 北京 100072)

0 引言

黏弹性胶体材料属于非牛顿流体，是一种半液半固黏稠状高分子聚合物，具有良好的弹性、可压缩性及流动性等优异的特点。将其装入特殊的密闭空腔机械结构中，起到减振、缓冲、吸能等效果，该装置即为黏弹性胶体阻尼缓冲器。黏弹性胶体在阻尼缓冲器中的启动流形式根据缓冲器机械结构可分为间隙流和孔隙流两种。

由于黏弹性流体独特的非线性，国内外众多学者根据不同的研究背景和黏弹性材料，选用不同的数学模型和本构关系研究阻尼缓冲器中黏弹性流体的流动特性。研究主要分为两类：一类为经验或半经验公式，这类研究公式推导基于大量试验数据，所推出的经验公式根据研究对象的不同而不同，使用限定条件较多，适用范围较为局限。另一类为经典模型及其衍生模型，其中以Maxwell模型最为典型。尤其随着分数阶导数的提出，分数Maxwell模型被证明可以较好地模拟黏弹性流体的流动过程[1-5]。Yang等[6]采用分数Maxwell模型研究了黏弹性流体在无限长管道中恒定压力梯度驱动下从静止开始的单向启动流动情况，求出了精确解。Yao[7]在逆行阶梯Maxwell模型基础上通过张量和不同分数阶导数定义将分数阶黏壶模型用于模拟大变形非线性黏弹性流体的流动。上述研究从数学角度很好地描述了黏弹性流体的流动特性，但值得注意的是，这些表达式模型参数往往通过数值方法得出，并不始终在物理和工程上保持合理性[8]。

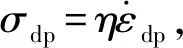
图1 弹簧壶元件原理图Fig.1 Schematic diagram of a spring-pot as an element

黏弹性胶体材料在阻尼缓冲器中运动时呈现非牛顿流体特性，具有较强的黏弹性，可采用分数Maxwell模型进行研究。但上述文献中均求得模型的解析解，然而分数阶微积分方程求解析解难度较大、过程较为复杂，计算机模拟时运算速度较慢；而数值解仿真模拟易于实现。并且采用以准态特性为参数的分数Maxwell模型模拟黏弹性流体在圆管内和平板间加速流动的启动流鲜有报道，同时在工程上用于研究阻尼缓冲器节流间隙和阻尼孔的分数Maxwell启动流模型也报道较少。

因此，本文针对黏弹性胶体在阻尼缓冲器阻尼孔和节流间隙中的启动流问题，构建以准态特性为参数的分数Maxwell模型，采用有限差分法求得模型的数值解，并设计启动流测试试验系统，验证分数Maxwell模型模拟黏弹性胶体阻尼缓冲器启动流的准确性。

1 分数Maxwell启动流模型构建

1.1 分数Maxwell模型

广义黏弹性模型是将弹簧与黏壶串联看作一个机构元件，其本构关系可写为

(1)

采用Maxwell模型串联两个弹簧壶机构元件(κ,α)和(ψ,β)(见图2)，其中κ、ψ分别为不同准态特性(Pa·sα、Pa·sβ)。由Maxwell模型关系可得

σa=σb=σ,

(2)

εa+εb=ε，

(3)

式中：σa和εa分别为弹簧壶a元件(κ,α)的应力与应变；σb和εb分别为弹簧壶b元件(ψ,β)的应力与应变；σ和ε分别为Maxwell模型的总应力与总应变。

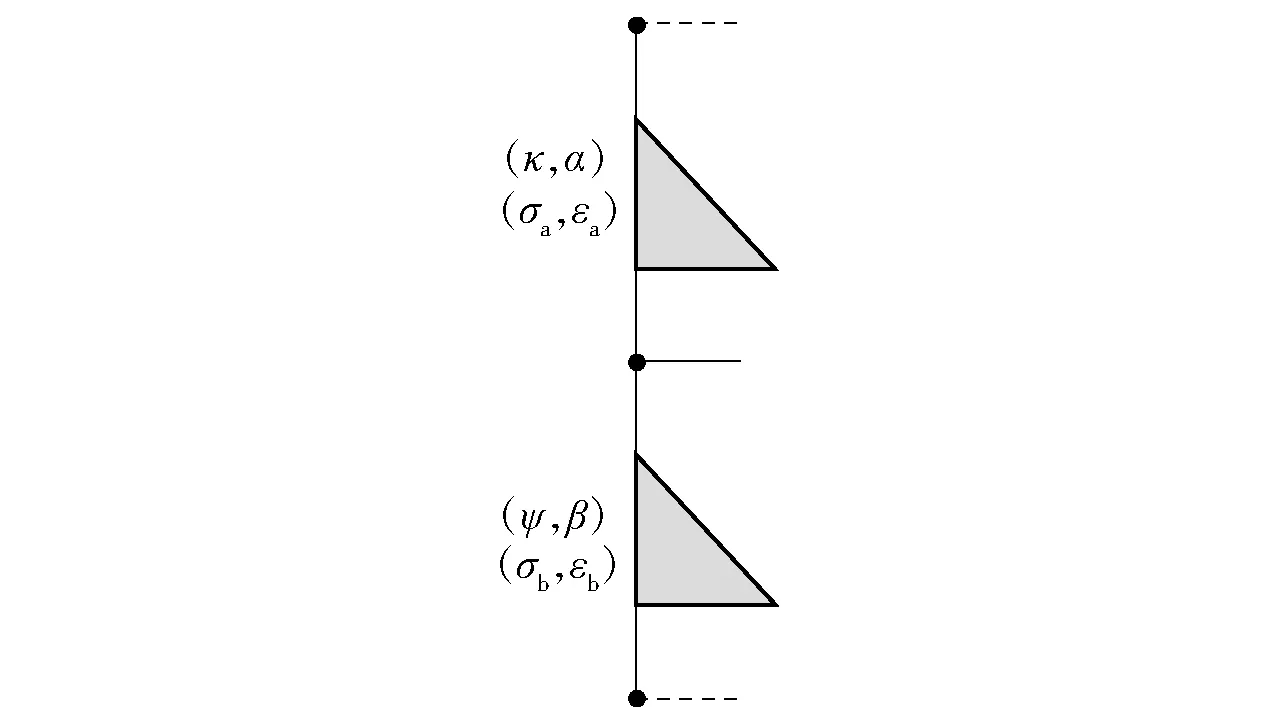
图2 分数Maxwell模型Fig.2 Fractional Maxwell model

将(1)式代入(2)式、(3)式，得

(4)

即分数Maxwell模型为

(5)

1.2 结构及简化

某型黏弹性胶体阻尼缓冲器结构如图3所示。阻尼缓冲器支座用于连接阻尼缓冲器和安装机构，起一定承力作用。将黏弹性胶体材料通过黏弹性胶体注入器注入阻尼缓冲器腔室中，根据需要调整黏弹性胶体材料的填充量，使阻尼缓冲器具有一定的预压力，称为初始预紧力。当阻尼缓冲器受到外界压力或冲击大于初始预紧力时，活塞杆推动活塞压缩阻尼缓冲器腔室内的黏弹性胶体材料。胶体材料被迫流过节流间隙和活塞上的阻尼孔，产生黏滞力，阻碍活塞前行，这一过程中外力转化为热能和势能，消耗和存储。当外力被撤消时，冲击力小于初始预紧力，黏弹性胶体材料自行膨胀，释放压缩过程中存储的势能，将活塞推回到初始位置，而通过阻尼孔和节流间隙被挤入前腔体的胶体材料流回后腔体，等待下次冲击或压力。

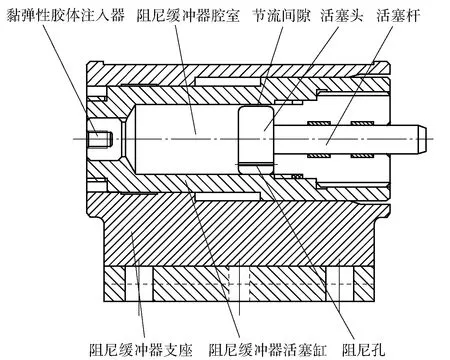
图3 某型黏弹性胶体阻尼缓冲器示意图Fig.3 Schematic diagram of a viscoelastic elastomer shock absorber

为符合黏弹性胶体阻尼缓冲器启动流时的实际工况，将黏弹性胶体在阻尼缓冲器阻尼孔和节流间隙中启动流的运动关系简化至二维空间中，分别看作流体在圆管内加速流动(见图4(a)，即流体在两平行板间以U=at的速度流动，而两平行板始终保持不动)和两平行板间一板不动、一板加速运动这两种形式(见图4(b)，即下板以U=at的速度向右移动，上板始终保持不动，流体由于黏性在下板的带动下向右流动)，图中L为阻尼孔或节流间隙间距，U=at表示流速，a为加速度。

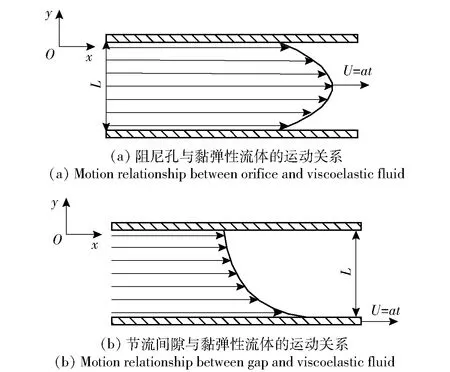
图4 阻尼缓冲器结构与黏弹性胶体的运动关系Fig.4 Motion relationship between shock absorberstructure and viscoelastic elastomer

1.3 控制方程

流体运动中总动量的时间变化率等于其自身体积力和相互作用表面力的总和。将加速度看作单位质量流体动量随时间的变化率，根据动量平衡率的牛顿运动定律可知：

Ma=∑F,

(6)

式中：M为质量；F为体积力和表面力总和。

与坐标系无关的运动方程矢量表达式为

(7)

式中：f为单位体积力；ρ为黏弹性流体密度；σ为应力张量。

考虑阻尼缓冲器中黏弹性流体介质运动时黏性较大、总质量较小，体积力远小于黏性力，因此将体积力忽略不计，则有

(8)

流速只在y轴方向有分布，则

(9)

式中：u(t,y)和σ(t,y)分别表示在t时刻空间位置y处的流速和应力。

(10)

(11)

由Riemann-Liouville分数阶微积分公式可知：

(12)

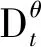
(13)

Γ(z)是伽马函数。

1.4 初始值和边界条件

当t≤0时，u(t)=0；当t>0时，阻尼孔启动流中心点的流速以加速度a逐渐增大，而靠近管壁的流速始终为0 m/s. 在节流间隙中，靠近运动板的流体流速随运动板以加速度a逐渐增大，而静止板附近的流速始终为0 m/s. 因此，初始条件和边界条件为

1)阻尼孔：

(14)

2)节流间隙：

(15)

1.5 无量纲分析

采用Π定理分析分数Maxwell模型的无量纲变量，

(16)

将(16)式的无量纲变量分别代入(10)式、(11)式中，得到分数Maxwell启动流无量纲方程(为简便起见，省略无量纲标记“*”)：

(17)

(18)

对应的阻尼孔和节流间隙的无量纲初始和边界条件为

(19)

(20)

1.6 数值求解

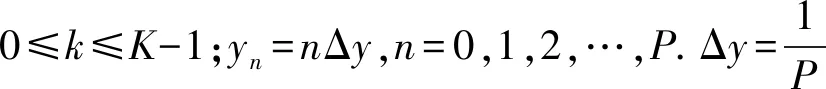
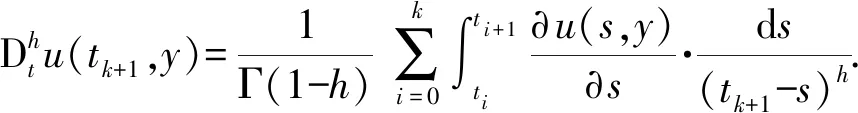
(21)

(22)

式中：o(Δt)为皮亚诺余项。

则

(23)

式中：t0=0；h0=1；hi=(i+1)1-h-i1-h，i=0,1,…,k.

同理，利用中心差分定理：

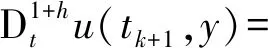
(24)

根据分数阶积分定义：

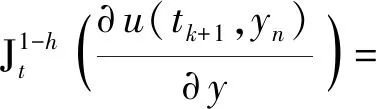
(25)

(26)

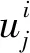
(27)

(28)

另外，牛顿流体模型根据(1)式可写为

(29)

(30)

2 数值计算结果及分析

将模型数值解和边界条件代入数学仿真软件MATLAB中，为保证结果收敛，选取时间步长Δt=0.001、空间步长Δy=0.025. 通过数值计算，对比分数Maxwell模型和牛顿流体模型的流动特性，选取基本模型参数为α=0.8、β=0.3、ζ=0.2.

2.1 阻尼孔数值模拟

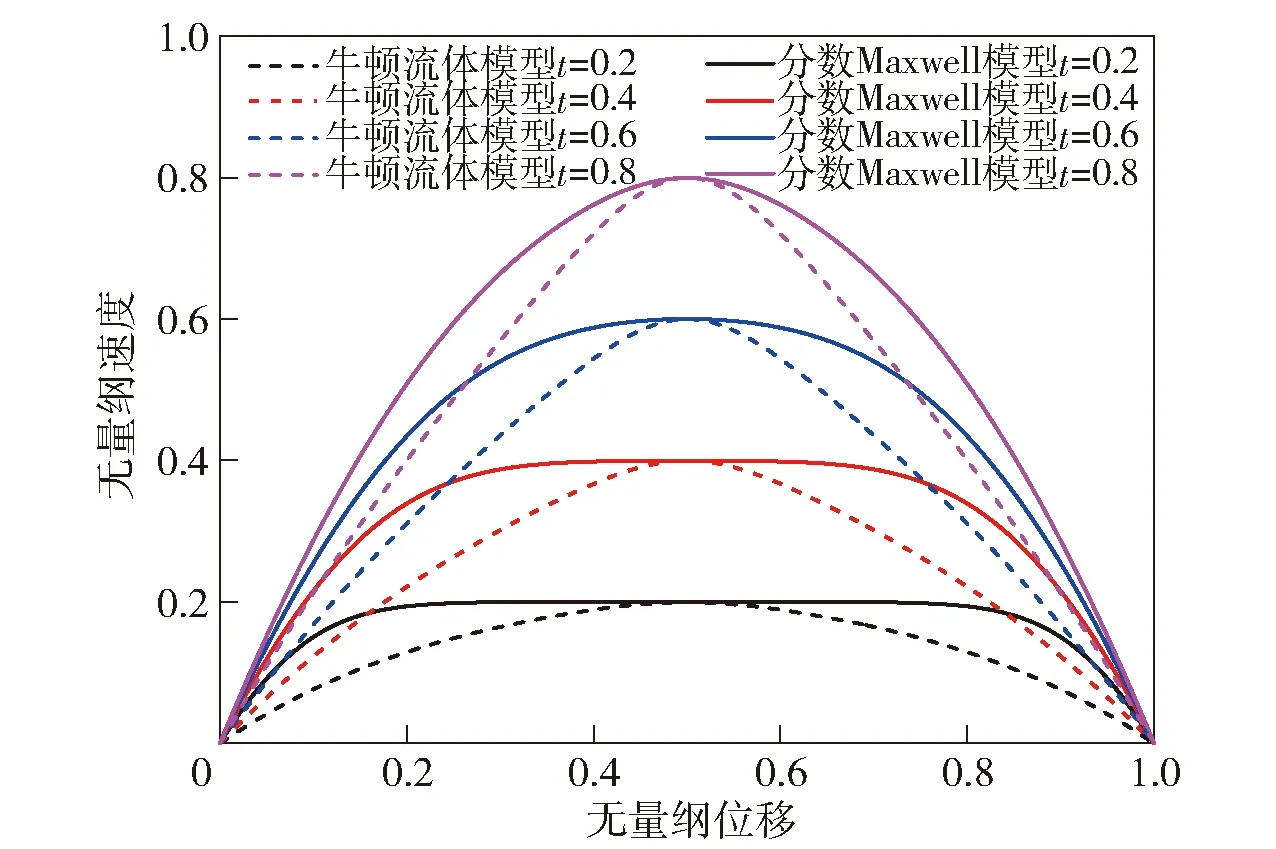
图5 阻尼孔流速分布Fig.5 Flow velocity distribution in orifice at different times

图5为分数Maxwell模型和牛顿流体模型随时间增大时阻尼孔流速的变化情况。从图5中可以看出，随着时间的不断增加，分数Maxwell模型流速分布曲线由扁平状逐渐发展为抛物线状，符合实际黏弹性流体的流动特性，且流速分布曲线保持着良好的非线性特点，曲线曲率较牛顿流体大。这意味着分数Maxwell模型模拟的流体始终保持着较好的黏弹性。

图6为阻尼孔中心点的流体应力变化情况。随着时间的增加，分数Maxwell模型和牛顿流体模型的应力均呈线性增长。由于分数Maxwell模型是通过广义黏弹性模型推导衍生而得，而牛顿流体模型则是广义黏弹性模型的一种特殊形式，因此二者应力变化趋势基本相同。但分数Maxwell模型应力小于牛顿流体模型。

取t=0.8，比较参数变化对分数Maxwell模型流速的影响，如图7～图9所示。参数α和β均为分数Maxwell模型的阶数，二者的变化情况对流场的影响基本一致，随着α和β的增加，分数Maxwell模型流体曲率逐渐下降，但变化不大。而ζ相比α和β对曲线曲率影响较大。从图9中可以看出，当ζ=0.1时流速曲率最大，而随着ζ的增加，流速曲率逐渐减小，并向牛顿流体发展。ζ与准态特性有关，而准态特性与松弛时间有关，松弛时间越长，材料越接近弹性体。这意味着ζ越大，黏度越小。

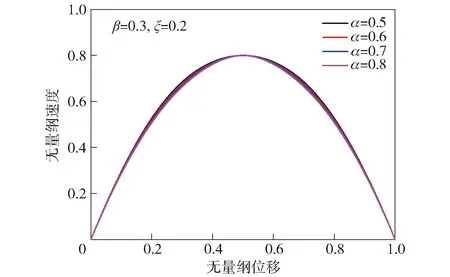
图7 不同α时分数Maxwell模型阻尼孔流速分布Fig.7 Flow velocity distribution of fractional Maxwell model in orifice for different α

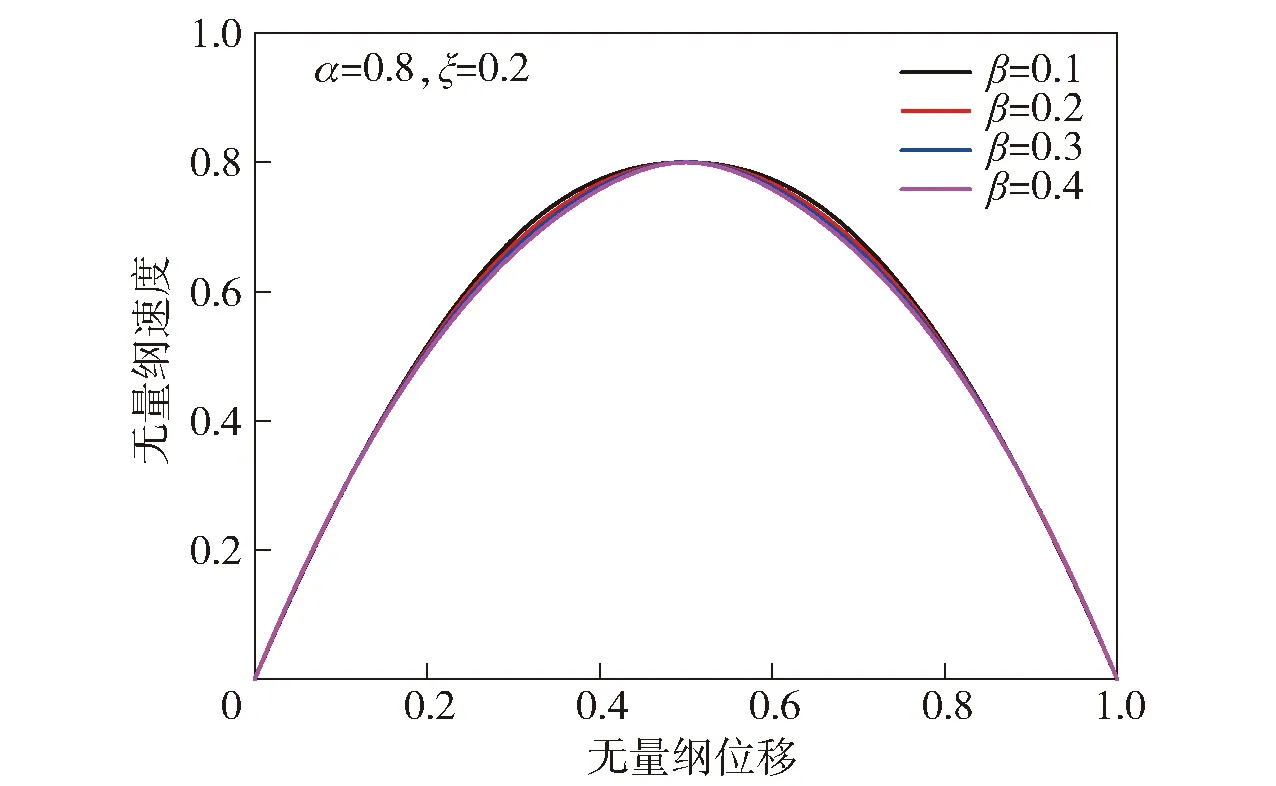
图8 不同β时分数Maxwell模型阻尼孔流速分布Fig.8 Flow velocity distribution of fractional Maxwell model in orifice for different β

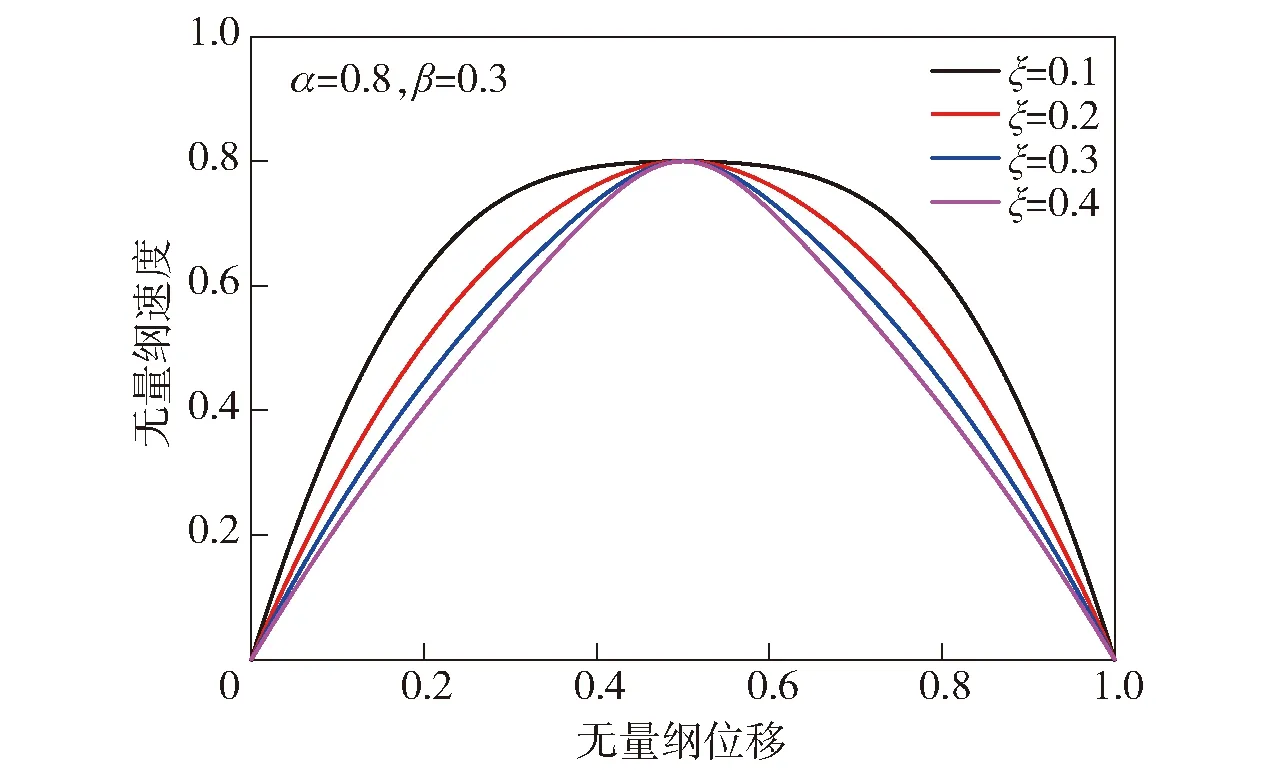
图9 不同ζ时分数Maxwell模型阻尼孔流速分布Fig.9 Flow velocity distribution of fractional Maxwell model in orifice for different ζ

2.2 节流间隙数值模拟

阻尼缓冲器节流间隙启动流流速分布随时间的变化情况如图10所示。从图10中可以看出，随着时间的增加，牛顿流体模型流速分布逐渐向直线形状发展，而分数Maxwell模型始终保持着良好的非线性。进一步证明了阻尼孔流速模拟的结果，分数Maxwell模型非线性良好，具有较强的黏弹性。

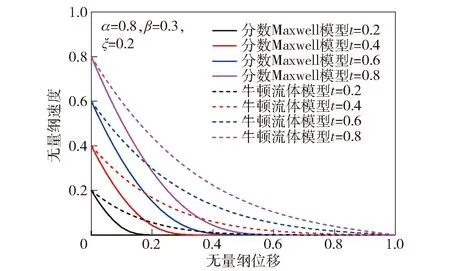
图10 节流间隙流速分布Fig.10 Flow velocity distributions in gap at different times

节流间隙启动流靠近移动平板一侧(y=0)应力分布曲线如图11所示。由图11可见，随着时间的增加，分数Maxwell模型与牛顿流体模型应力均呈线性增长，该结果与阻尼孔启动流应力分布增长趋势一致。当t=6时，分数Maxwell模型和牛顿流体模型节流间隙启动流应力值分别为1.33和1.52，而阻尼孔启动流应力值分别为2.17和2.54；分数Maxwell模型和牛顿流体模型阻尼孔启动流的应力分别为节流间隙启动流应力的1.63和1.67倍。原因在于，阻尼孔启动流最大速度发生在平板间距中心点处(y=0.5)，而节流间隙启动流最大速度出现在靠近移动平板一侧处(y=0)，二者边界条件不同。当时间和空间步长相同时，阻尼孔启动流计算所得速度数据是节流间隙启动流数据数量的一半。应力通过速度差值计算所得，而分数Maxwell模型和牛顿流体模型应力均呈线性增长，致使阻尼孔启动流应力值远比节流间隙启动流大。虽然减小步长可以使流速数据数量保持一致，但步长的调整会导致差值系数发生变化，因此计算结果将保持不变。

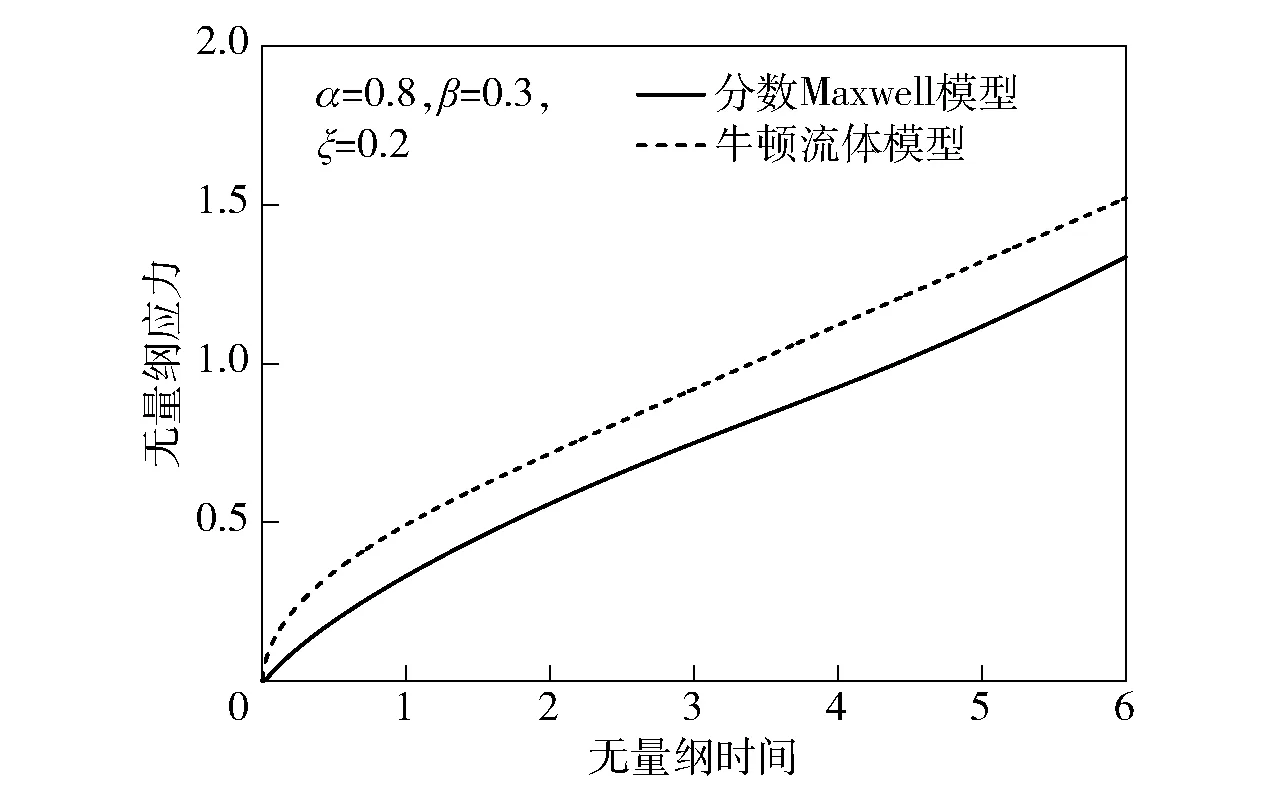
图11 节流间隙靠近移动平板一侧应力分布Fig.11 Stress distribution in gap near the side of the moving plate

3 试验验证

试验系统由伺服电机、电机控制器、玻璃管缓冲器、高速相机、图像采集平台和射灯光源组成，如图12所示。为了方便捕捉黏弹性流体流动过程，采用塑料管作为活塞，玻璃管作为缓冲器腔壁，并按照缓冲器活塞和阻尼孔实际尺寸设计试验装置，其中腔体内壁直径20 mm，活塞厚度15 mm，阻尼孔直径2.5 mm. 为方便拍摄阻尼孔的流动过程，取消活塞与腔壁之间的间隙，并在塑料管活塞头部安装密封圈，防止运动过程中有黏弹性流体从缝隙中挤入。

图12 启动流试验测试系统Fig.12 Test system for the start-up flow

采用日本Mitsubishi公司生产的交流伺服电机作为速度源推动活塞运动，通过电机控制器调整转速，使活塞杆始终保持恒定速度或加速度。利用美国Fastec公司生产的HiSpec 5 高速相机和配套的图像采集平台捕捉活塞启动时黏弹性流体在阻尼孔中的流动情况。其中，拍摄过程中采用射灯作为辅助光源以提高相机识别度。

在玻璃管缓冲器腔体中注入主体成分为甲基硅氧烷的黏弹性胶体材料，其动力黏度为5×105mm2/s，密度为1.1 kg/m3，调节电机控制器使活塞杆速度从0 mm/s启动，加速度始终保持1.0 mm/s2，在常温下进行试验。高速相机采集频率为500帧，记录下不同时刻黏弹性流体流动情况，如图13所示，图13中黑色部分为黏弹性胶体材料，白色部分为塑料管活塞。试验过程中辅助光源在玻璃管缓冲器左侧，高速相机拍摄时左半部分容易出现反光点，导致试验结果左侧有部分区域出现缺失，变为白色。由于加速度较小，前0.6 s流体速度也较小，胶体变化不明显。

图13 高速相机记录下阻尼孔启动流运动情况Fig.13 Test results of start-up flow in orifice

采用表1所列模型参数，代入分数Maxwell模型中得到阻尼孔启动流流速随时间的变化结果。对速度进行积分，获得分数Maxwell模型流体的液面高度分布曲线，如图14所示。对比观察试验和模型结果可知：阻尼孔中心位置流速最大，而靠近阻尼孔边缘位置流速较小；随着时间和活塞速度的增大，试验和数值结果的变化趋势相同，液面形状均从扁平状逐渐发展成为抛物线状，且阻尼孔启动流过程始终保持着较强的黏弹性。

表1 分数Maxwell模型参数

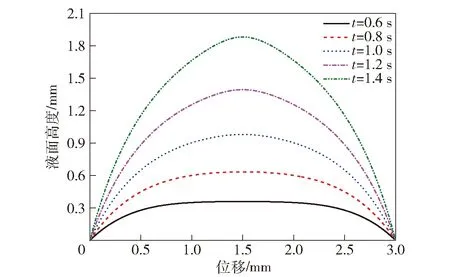
图14 分数Maxwell模型阻尼孔流体液面高度分布Fig.14 Fluid level distribution of fractional Maxwell model in orifice

其中，松弛模量Gt、松弛时间λ和分数阶指数α、β通过动态模量理论公式与试验数据拟合而得(见文献[20])；而准态特性参数κ和ψ[21]通过上述参数近似获得：

(31)

以t=1.0 s时黏弹性胶体液面分布试验结果为例，提出最大液面高度H和最大曲率距离d两个考量参数，如图15所示。最大液面高度为黏弹性流体启动时初始位置到当前时刻液面最高点的垂直距离，是检验同一时刻模型结果与试验结果的一致性。最大曲率距离是从液面最高点到液面最低点做辅助线，平行于辅助线的最大液面切线到辅助线之间的距离，主要用来考察流体的黏弹性。根据实际标尺，测量最大液面高度和最大曲率距离，结果如表2所示，其变化趋势如图16和图17所示。

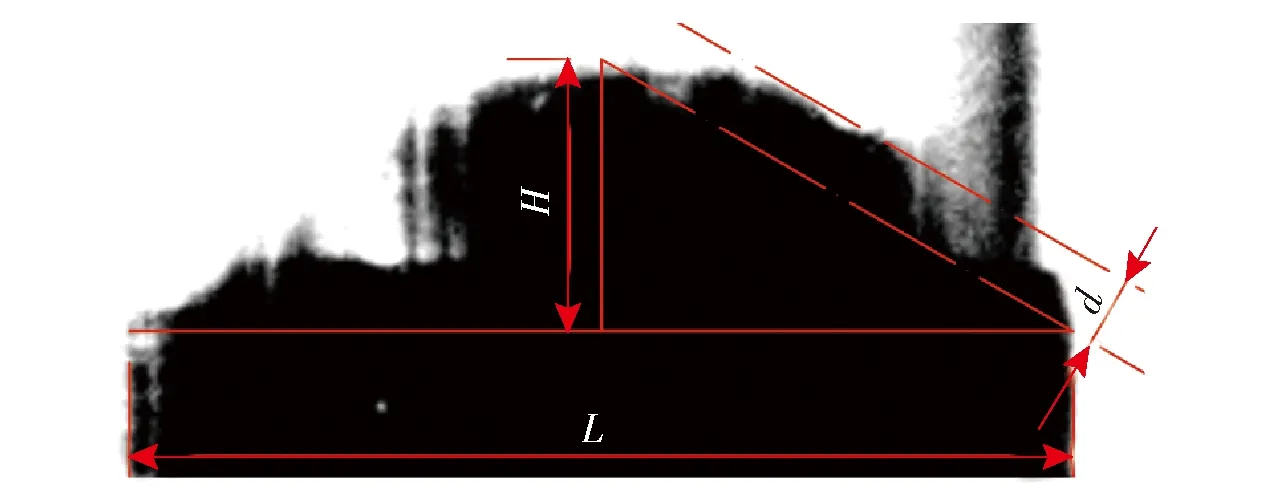
图15 黏弹性流体液面测量方法Fig.15 Viscoelastic fluid level measurement method

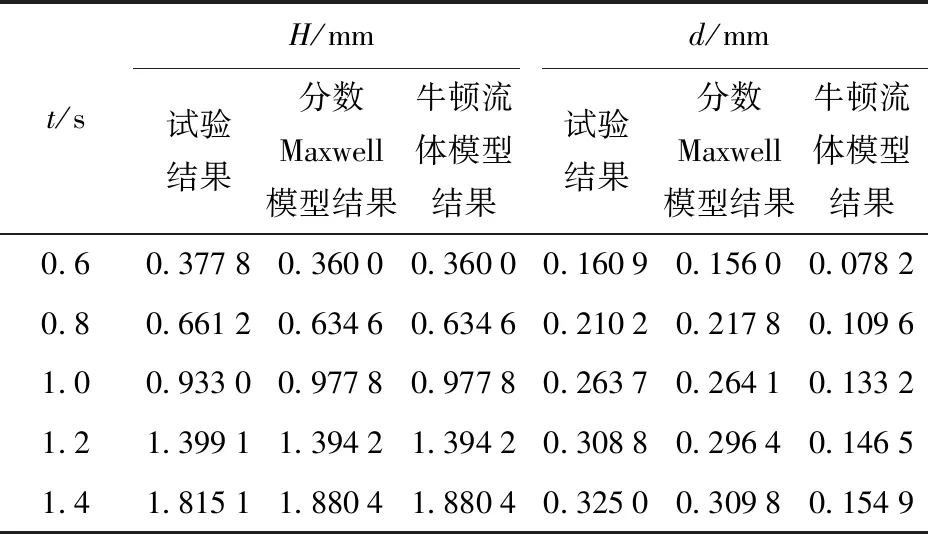
t/sH/mmd/mm试验结果分数Maxwell模型结果牛顿流体模型结果试验结果分数Maxwell模型结果牛顿流体模型结果0.60.37780.36000.36000.16090.15600.07820.80.66120.63460.63460.21020.21780.10961.00.93300.97780.97780.26370.26410.13321.21.39911.39421.39420.30880.29640.14651.41.81511.88041.88040.32500.30980.1549

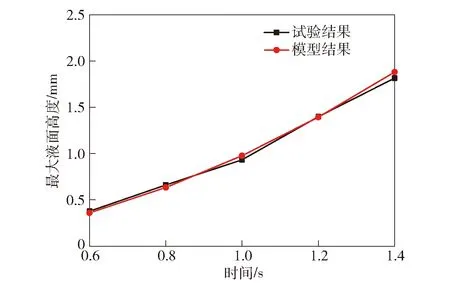
图16 最大液面高度结果对比Fig.16 Comparison of measured and simulated maximum fluid levels

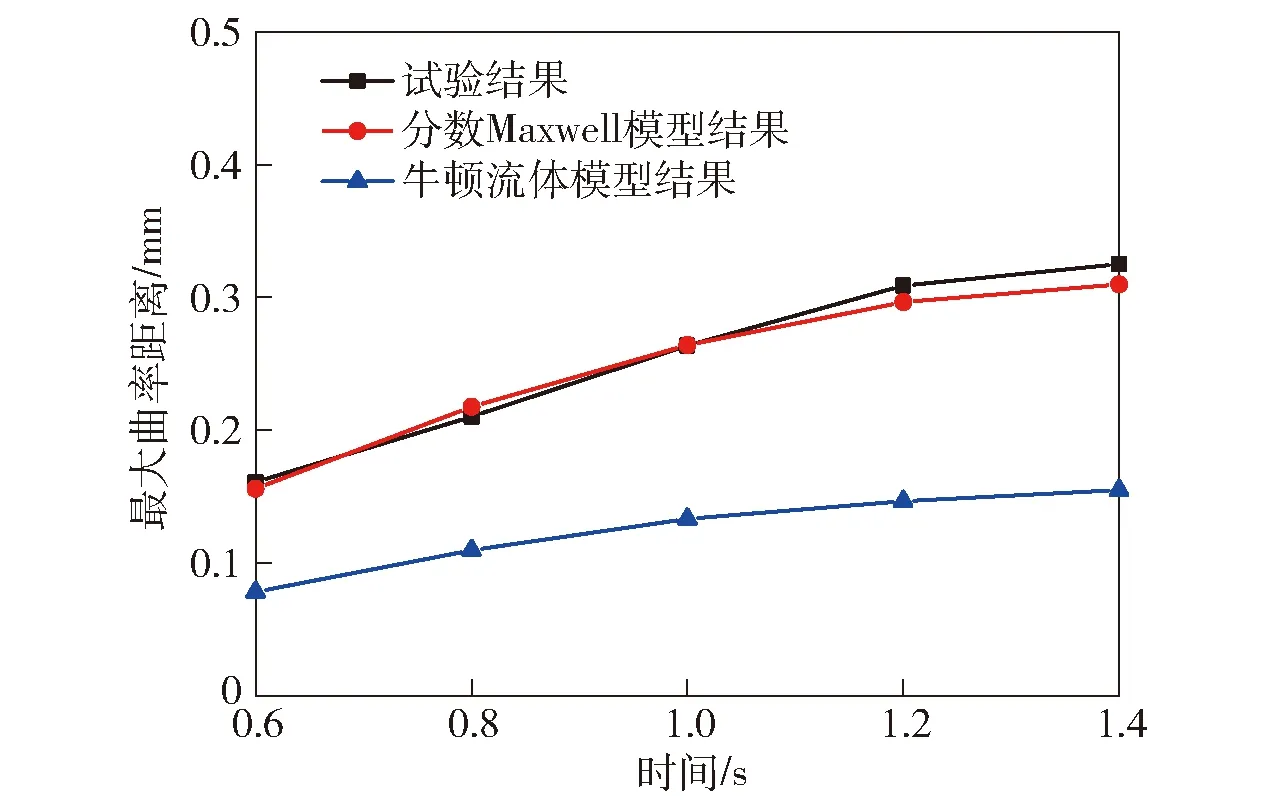
图17 最大曲率距离结果对比Fig.17 Comparison of maximum curvature distances

结合图16、图17及表2可知：牛顿流体模型随着时间的增大，最大曲率距离有趋向于稳态的趋势，模型的黏弹性很弱；而分数Maxwell模型结果与试验结果吻合较好，其中最大液面高度最大误差为4.79%，最大曲率距离的最大误差4.67%，如图18所示。由此可见，分数Maxwell模型可以很好地描述黏弹性胶体的黏弹性特点，准确地模拟黏弹性胶体在阻尼孔中启动流的实际流动过程。

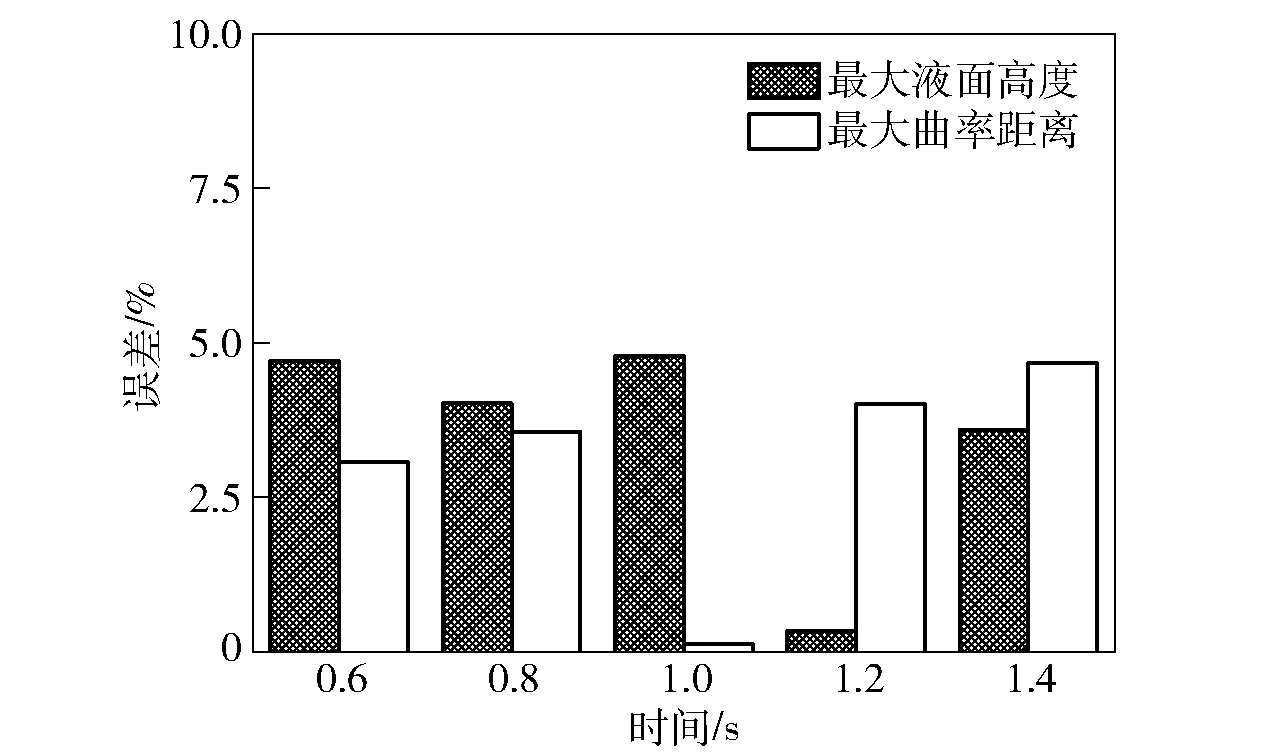
图18 分数Maxwell模型的误差Fig.18 Errors of fractional Maxwell model

4 结论

本文根据黏弹性胶体在阻尼缓冲器阻尼孔和节流间隙中的实际流动情况，将其简化为黏弹性流体在圆管内加速流动和两平行板间一板不动、一板加速运动两种单向加速启动流形式，根据实际工作环境设定初始和边界条件，提出并构建了含准态特性参数用于研究黏弹性胶体阻尼缓冲器启动流的分数Maxwell模型，采用有限差分方法求得了模型的数值解。通过与牛顿流体模型进行对比，分析了流速和应力的变化情况及各参数对流速的影响。最后，设计了试验系统，捕捉了启动流时黏弹性胶体材料在阻尼孔中的流动过程。通过定义、测量和对比分数Maxwell模型模拟结果与试验结果的最大液面高度和最大曲率距离验证了模型的准确性。得出以下结论：

1)黏弹性流体在圆管内和两平行板间加速流动时，分数Maxwell模型流速分布始终保持着良好的黏弹性。

2)分数Maxwell模型与牛顿流体模型应力呈现线性增长趋势。

3)随着参数α、β和ζ的增加，分数Maxwell模型流速分布曲线曲率逐渐下降，其中ζ对曲线曲率的影响比α和β大。

4)启动流试验测试系统捕捉到的黏弹性胶体在阻尼孔中启动流形状从扁平状逐渐发展成为抛物线状，且中心点处速度最大，流动过程具有较强的黏弹性。该结果与分数Maxwell模型模拟结果变化趋势相同。

5)分数Maxwell模型模拟结果的最大液面高度和最大曲率距离与试验结果较为吻合，其最大误差分别为4.79%和4.67%，证明了模型的准确性。

因此，分数Maxwell模型可准确地模拟黏弹性胶体在阻尼缓冲器阻尼孔和节流间隙中启动流的流动情况，可用于指导黏弹性胶体阻尼缓冲器的设计。