基于改进PSO 算法的箱式火箭炮机动路线选择
2019-11-06石怀龙李臣明马雁楠
石怀龙,李臣明,马雁楠
(陆军炮兵防空兵学院南京校区,南京 211132)
0 引言
箱式火箭炮是我陆军火力打击装备体系的重要组成部分,在信息化作战背景下,箱式火箭炮将更加注重机动作战、快速作战、精确作战,以达到增强火力打击突然性、提高己方力量战场生存率的效果[1]。为实现此作战要求,箱式火箭炮必须科学、快速地选择机动路线。
当前学术界对于机动路线选择相关问题的研究较多,方法各异。李伟等[2]建立了包括符合战术意图、地形状况、装备性能状况、指挥保障在内的机动作战路线选择的指标体系,利用模糊数学法对机动作战路线进行选择,实现了由定性分析向定量分析的转化;路建伟等[3]采用蚁群算法原理较好地模拟出了现代战场复杂环境对防空兵兵力机动路线选择的影响等等。本文在充分探讨研究指标科学性的基础上,采用基于改进PSO 算法来解决机动路线选择问题。
1 箱式火箭炮机动路线选择问题及其影响因素
1.1 问题描述
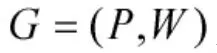
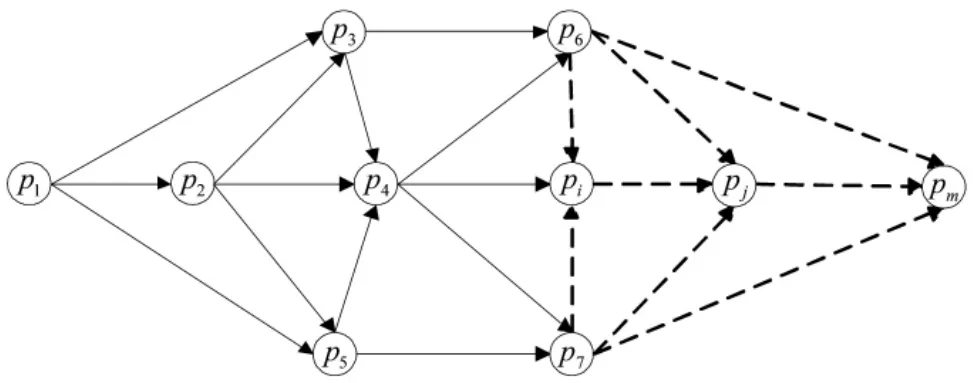
图1 机动路线示意图
1.2 影响因素的选择与建模
1.2.1 影响因素的选择
考虑箱式火箭炮在实施机动作战过程中的实际情况,本文选取4 个影响因素作为研究对象,分别为:机动距离、道路状况、机动时间和机动安全性。根据问题描述及设定情况,分别对确定的4 个影响因素展开建模和分析。
1)机动距离
设第i 点至第j 点任意相邻节点路段的机动距离为dij,则dij可通过查询纸质地图、数字地图等手段获得。
2)道路状况

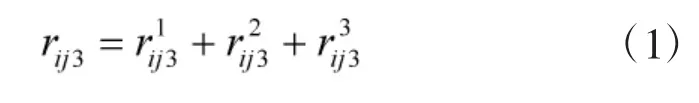
3)机动时间
设箱式火箭炮部(分)队通过第i 点至第j 点任意相邻节点的机动时间为tij,则tij的值可通过式(2)求得:
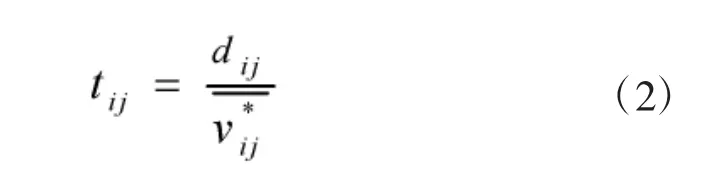
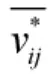
4)机动安全性
根据箱式火箭炮的使用原则,通常可配置在距敌战斗防御前沿较远的位置,敌常规的侦察和火力打击手段难以对我造成实质威胁。这里只把箱式火箭炮在机动时被敌航空(飞机)或天基(卫星)侦察发现的概率和遭敌远程火力(导弹)攻击后毁伤概率作为研究机动安全性问题主要的研究对象[4]。
设第i 点至第j 点任意相邻节点路段的机动安全性为sij,敌侦察发现目标的概率为rij,遭敌远程火力攻击后毁伤的概率为cij,则机动安全性为sij可通过式(3)求得:

其中,
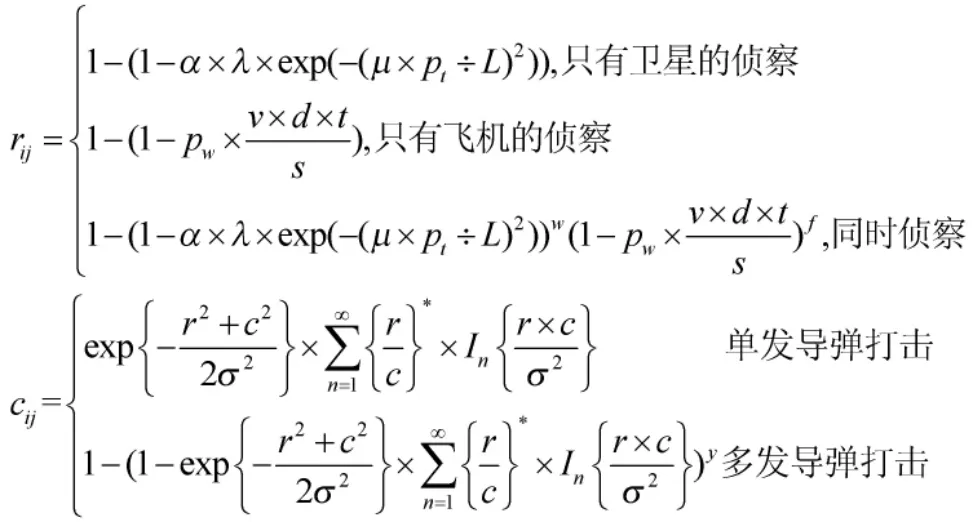
式中,pw为武器装备的被识别率;v 为侦察飞机的飞行速度;d 为侦察飞机的搜索宽度;s 为机动区域;t为侦察飞机的侦察时间。r 为目标与背景光度;α 为气象因子;μ 为目标形状修正因子;pt为卫星的分辨率;L 为目标的几何尺寸。r 为等效圆目标半径;c 为导弹系统偏差;
1.2.2 影响因素的无量纲化处理
根据以上分析,建立4 个影响因素的数学模型,但由于各个影响因素的量纲不同以及数值在数量级上悬殊较大,为方便下一步计算,要对它们进行无量纲化处理,使其统一量纲。这里采用比重法对各影响因素进行无量纲化处理[5]。
比重法的计算公式为:
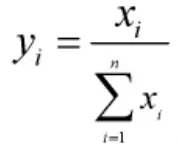
因此,对于各影响因素的无量纲化处理可按照式(4)进行。
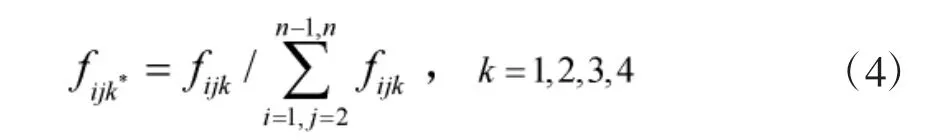
通过无量纲化处理后的值,不能直接用于后续模型的计算,其原因在于有的影响因素要求其值越大越好,如机动安全性;有的影响因素要求其值越小越好,如机动时间。这里规定各影响因素的无量纲化值越小越好。对于值越大越好的因素,用1 减去它,得到新的无量纲化值。统一后的各影响因素无量纲化值可用式(5)表示:

1.2.3 影响因素权重的确定
权重是指在某一影响因素在所有影响因素中的重要程度。在分析机动路线选择的影响因素时,本文选择了4 个影响因素作为研究对象,这4 个影响因素在不同的战场环境下的重要性通常是不同的。如在作战中,当敌方占据信息优势时,在进行机动路线选择决策时,机动安全性的权重会考虑的多一些;当我方占据信息优势时,机动距离和机动时间的权重则会考虑的多一些。对于指挥员而言,要根据战场实际情况,灵活确定各影响因素的权重。其方法可采用序关系分析法确定指标的权重系数[6],具体步骤如下:
第4 步:计算权重系数。计算公式为:
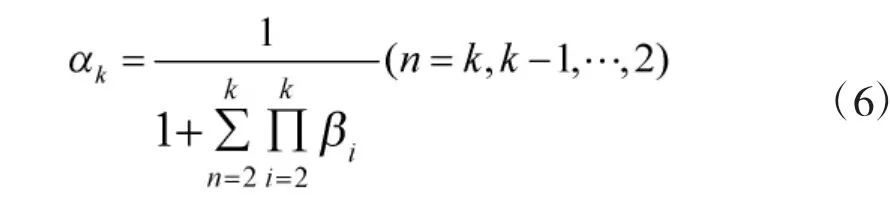
1.2.4 综合评价值模型的确定
根据式(5)中无量纲化处理后得到的值在和在式(6)中确定各影响因素权重值的方法,可按式(7)计算出各路段的综合评价值:
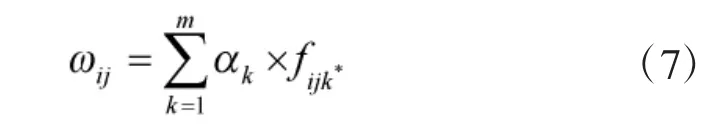

表1 βn 取值参考表

根据以上建立的模型及分析可知,从起点至终点的各路段综合评价值之和最小的某条机动路线即为最优路线。确定这一条最优的机动路线的方法有很多,如利用网络模型或者枚举的方法。这里采取一种基于改进PSO 算法的方法进行求解。
2 粒子群算法及其改进
2.1 粒子群算法
粒子群算法(PSO)是1955 年由美国学者J.Kenney 和R.C.Eberhart 率先提出。在PSO 中,每个粒子视为优化问题的可行解,且每个粒子具有一定的速度以决定其方向和距离。PSO 通过初始化一群随机粒子,这些粒子追随当前的最优粒子在解空间中搜索,通过不停迭代最终找到最优解。在每一次迭代中,粒子通过跟踪两个极值来更新自己:一个是粒子本身当前找到的最优解,另一个是整个群体当前找到的最优解。找到这两个极值时,每个粒子根据式(8)来更新自己的速度和位置:
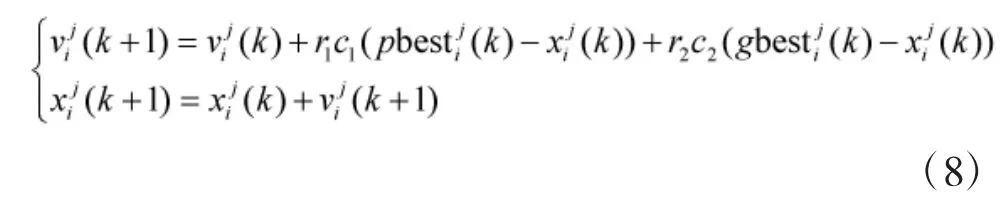
2.2 粒子群算法的改进
PSO 算法在实际运用中体现出很多优点,如参数少、结构简单、鲁棒性高、易实现等特点。但还有许多不完善的地方,如当本身信息和个体极值信息占优势时,算法容易陷入局部最优解等。Y.Shi[7]等提出通过增加一个惯性权重c0来协调PSO 算法的全局和局部寻优能力,见式(9)。得到新的粒子群算法模型受到广泛运用,此算法也被称为标准粒子群算法。
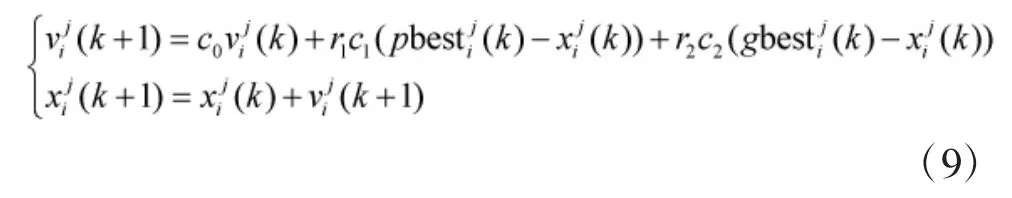
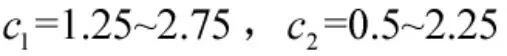
2.3 粒子群算法基本步骤
粒子群算法的基本步骤如图2 所示。
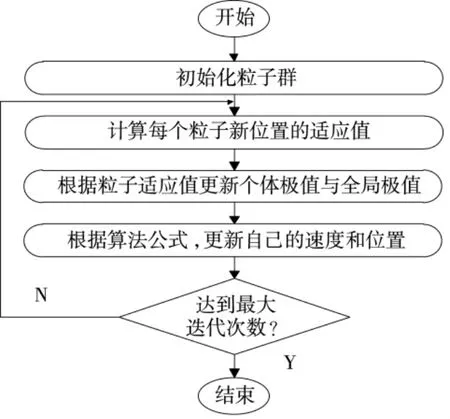
图2 粒子群算法基本步骤
3 基于改进PSO 算法的机动路线选择方法
3.1 带权有向图邻接矩阵的定义
设选定的地图中共有n 个节点,将计算完各路段综合评价值的地图看作一个带权有向图,使用赋权的邻接矩阵将其表达成一个n×n 的矩阵。其基本思想为:对于有n 个节点的图,用一维数组node[n]依次存储节点信息,用二维数组Route[n][n]存储节点之间关系的信息。该二维数组称为这个带权有向图的邻接矩阵。在邻接矩阵中,以节点在node[n]数组中的下标代表节点,邻接矩阵中的元素Route[i][j]存放的是顶点i 到顶点j 之间的综合评价值。
3.2 改进PSO 算法的原理
在本文中,每一个粒子的代价函数是该粒子所选择的路径的综合评价值。将每一个粒子设置为一个一维数组,该数组有n 个元素,每个元素表示经过某一条路径的综合评价值。若整个环境中有m 个数组,则所有的粒子可以用一个m×n 的矩阵表示。每一个粒子都由n 个元素组成,分别表示模型中经过的n 段路线,共同组成了该粒子选择的某一条路径。再计算该粒子中所有元素的和,即该路径中所有路线的总体评价值,将其作为该粒子的适应值。适应值越小,总体评价值越低,粒子越优。所有粒子通过历史最优适应值数组pbest[m][n]和全局最优适应值数组gbest[n]来更新自己的位置。
3.3 改进PSO 算法步骤
为便于数值计算,给出基于改进PSO 算法的机动路线选择方法的算法步骤:
步骤1:定义参数如下:节点数n、节点信息数组node[n]、节点关系数组Route[n][n]、粒子总数m、最大迭代次数Dmax、最大速度Vmax、最远距离Xmax、惯性权重c0、加速因子r1r2、全部粒子的位置数组Position[m][n],全部粒子的速度数组Velocity[m][n]、历史最优位置数组pbest[m][n]、历史最优适应值数组Vpbest[m][n]、全局最优位置数组gbest[n]、全局最优适应值数组Vgbest[n]、当前粒子历史最优适应值数组Lpbest[n]、当前粒子全局最优适应值Lgbest;
步骤2:对每个粒子初始化并检查其有效性,随机产生n 个初始解,随机产生n 个初始速度,令当前迭代次数归零;
步骤3:通过计算每一个粒子的适应值,将其放入Lpbest[n]中,比较Lpbest[n]与Vpbest[m][n]的大小,将更小的值赋予Vpbest[m][n];
步骤4:将所有Vpbest[m][n]与Vgbest[n]相比较,将更小的值赋予Vgbest[n];
步骤5:根据式(9)更新每一个粒子的速度与位置;
步骤6:检查新的速度和位置是否超过Vmax与Xmax,若超出,则放弃本次的速度和位置更新;
步骤7:随着迭代次数增加线性减少c0的取值,检查迭代次数是否达到Dmax,是则转到步骤8,否则转到步骤5;
步骤8:迭代结束,gbest[n]即为找到的最优路径。
4 算例分析
某箱式火箭炮营计划从p1阵地机动到p8阵地。参谋人员通过前期调查将机动路线及可能经过的节点绘制成图,见图3。将各路段影响因素的相关信息绘制成表2,通过战场形势分析,指挥员确定各影响因素的权重系数向量为{0.2、0.1、0.4、0.3}。假设所列路段路况均满足箱式火箭炮营行军要求,且机动过程中营行军编队可视为一个点。则该营指挥员如何选择最优的机动路线?
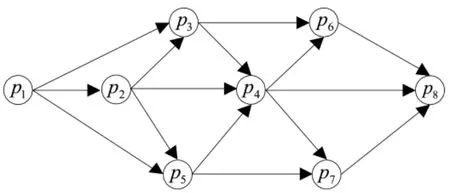
图3 某营机动路线示意图
设不直接通达的两点之间的综合评价值为-1,将各点间的综合评价值用矩阵形式表达如下:

为验证算法有效性,运用标准PSO 和本文提出的改进PSO 分别对该算例进行计算。设定参数如下:惯性权重c0=0.5;学习因子c1=c2=2;节点数n=8;粒子总数m=50;最大迭代次数Dmax=100;最大速度Vmax=25;最远距离Xmax=100。
两种算法的运行结果如下页表4 所示,两种算法的进行迭代对比如图4 所示。
根据表4 运算结果可知,使用标准PSO 算法和改进PSO 算法的最优值都是收敛于1.184,最优路径为1→3→4→8。故该营指挥员应选择1→3→4→8 作为机动路线。从中也可以看出改进PSO 算法在搜索成功率和耗时上都优于标准PSO 算法。

表2 各路段影响因素信息

表3 各路段的综合评价值
从图4 两种算法迭代对比可以看出,采用标准PSO 算法经过约70 次迭代实现了最终收敛,而采用改进PSO 算法只经过约50 次迭代即实现了最终收敛,且收敛速度更快。
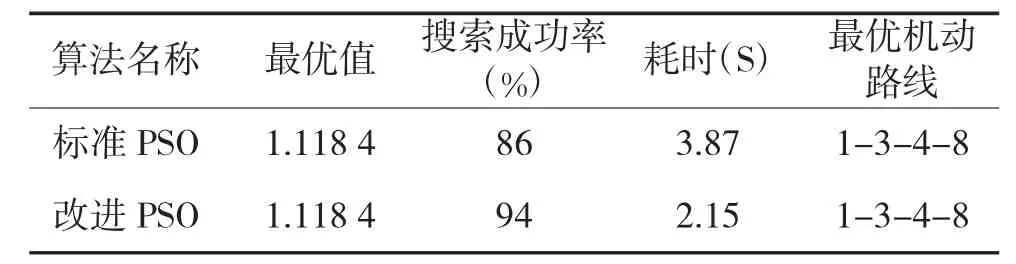
表4 两种算法运行结果对比
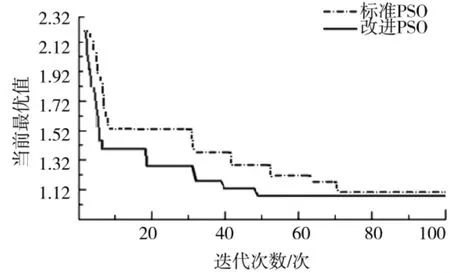
图4 两种算法迭代对比
5 结论
本文分析了箱式火箭炮机动路线选择的影响因素,构建了综合评价值模型,利用改进PSO 算法进行机动路线选择寻优,通过算例分析证明了其可靠性,与此同时也显示出改进PSO 算法在搜索效率、收敛速度上都优于标准PSO 算法,证明了本文采用的改进PSO 算法求解箱式火箭炮机动路线选择问题效果较好。
