一种对陆攻击飞行器命中精度概率圆检验方法*

郑小兵，李 曦，王宝和，李玉杰

（解放军91550 部队，辽宁 大连 116023）

0 引言

武器系统命中精度评定问题是装备试验鉴定工作中的一个重要环节，往往试验子样数的确定以及飞行试验方案的制定都与其息息相关。命中精度评定的本质是通过获取的试验信息对飞行器精度进行统计推断，包括假设检验方法和参数估计方法，不仅需要对命中精度是否满足设计指标给出判断，还需要对命中精度的实际达到水平给出估计，在把住武器交付关口的同时，进一步摸清性能底数。命中精度评定中的假设检验问题和参数估计问题分属于两个研究范畴，本文重点对对陆攻击飞行器命中精度圆概率偏差指标的检验问题进行讨论［1］。

新型对陆攻击飞行器相比于早期的弹道式飞行器，采用卫星组合导航系统和末制导识别系统后，命中精度水平有了质的提高。影响命中精度的误差因素发生了根本性的变化，原来作为主要误差成分的自控终点散布误差影响趋近于零，取而代之的是导引系统的跟踪误差和控制系统的控制误差，尤其是动态控制精度受自然风干扰和气动力干扰的影响较大，成为了对命中精度影响最显著的误差源。命中精度指标是定义在最大风干扰条件下的，但是实际打靶试验中每次都安排在最大风干扰条件下进行是不现实的，如何使用不同风干扰条件下的试验结果，对命中精度进行检验是本文重点讨论的问题。

1 问题的提出

影响对陆攻击飞行器命中精度的误差源大体分为两类，前视成像导引系统的目标跟踪点误差和飞行器控制系统的控制误差。目标跟踪点误差包括前视跟踪角误差和瞄准点误差，前视跟踪角误差取决于伺服系统死区、非线性和角度分辨率，瞄准点误差取决于目标基准图保障精度和目标识别精度。控制系统误差主要包括动态控制精度和传感器测量误差，动态控制精度受风干扰及气动力/力矩干扰的影响较大，其影响程度取决于风速、风向、马赫数变化量、姿态变化快慢等诸多因素，传感器测量误差引起的控制误差包含速度误差引起的控制误差和视线角延迟误差引起的控制误差。综上所述，对陆攻击飞行器命中精度的误差分配如表1 所示。

表1 中给定的数据进行了归一化处理，且误差数据除圆概率误差外，均为1 倍方差条件下的误差分布。

观察表1，可以看到风干扰误差是影响飞行器命中精度的主要误差源，影响最大时可以占到误差总量的70%左右，并且其他误差源在不同风速下的干扰基本不变。命中精度指标是定义在最大风速条件下的，飞行试验一般是在不同风速（小于最大风速）条件下组织实施的，如果直接使用飞行试验脱靶量误差对命中精度进行检验显然是不准确的。

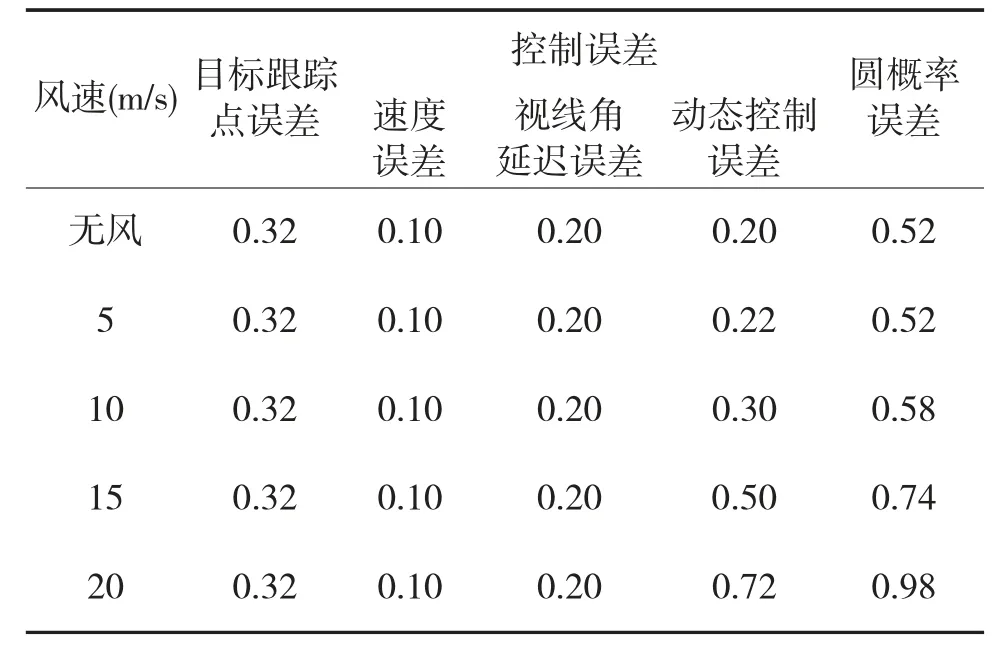
表1 命中精度误差分配

如何充分利用现有飞行试验信息对命中精度指标进行科学的检验是需要研究解决的问题，常规方法是对不同风速条件下的脱靶量进行精度折合，折算到最大风速条件下的脱靶量，然后再进行命中精度指标检验。但是这种精度折合的方法有两个方面的弊端，一方面精度折合方法比较复杂，需要进行飞行弹道的力学分析，计算结果不直观；另一方面精度折合结果受到计算条件影响较大，设置不同初始参数往往得出差异较大的计算结果。因此，这种精度折合的检验方法很容易引起质疑，下面讨论一种基于实际脱靶量结果对命中精度指标进行直接检验的工程实用方法。

2 概率圆检验方法

2.1 圆概率偏差指标

飞行器的精度指标一般包括射击准确度和射击密集度两个要求，不仅要求飞行器有一定的密集度，而且对落点散布中心离开目标的距离也有要求。根据飞行器命中精度误差源机理特性、数理统计中的中心极限定理以及长期积累的工程经验，可以假定飞行器落点偏差服从正态分布［2］。

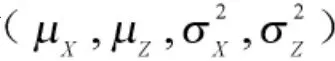
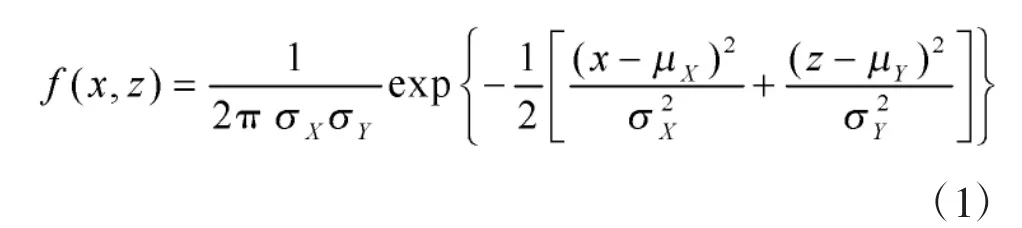
此时圆概率偏差R 满足关系式：

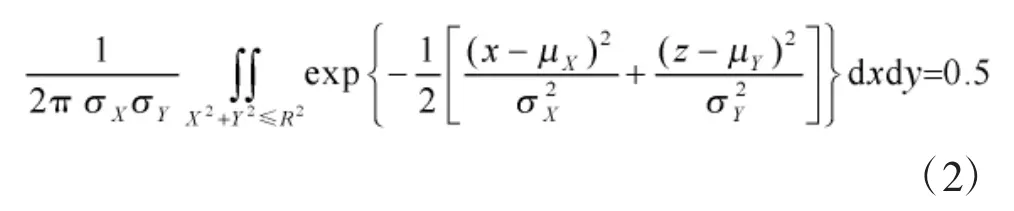
对于命中目标区时系统误差（射击准确度）远小于随机误差（射击密集度），即μx、μy 可以近似为零。此时圆概率偏差与射击密集度存在以下关系：

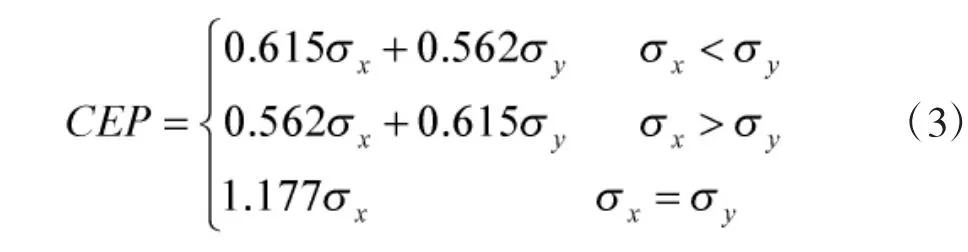
2.2 概率圆检验方法

飞行器命中精度检验中，往往采用下列简单假设：

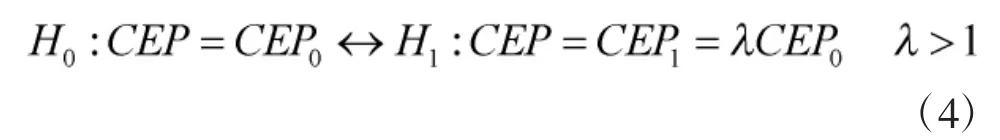
其中，CEP0为给定的要求值，为检出比，由研制方和使用方共同协商事先确定。

不妨假定对应于原假设的射击准确度和射击密集度分别为

而对应于备择假设的射击准确度和射击密集度分别为

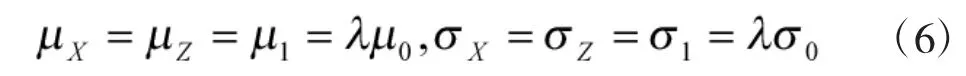
假定共进行了n 次试射，令m 为落入以R 为半径的圆内的飞行器数，取m 为统计量，则

研制方风险α（即弃真概率）和使用方风险β（即采伪概率）分别为：

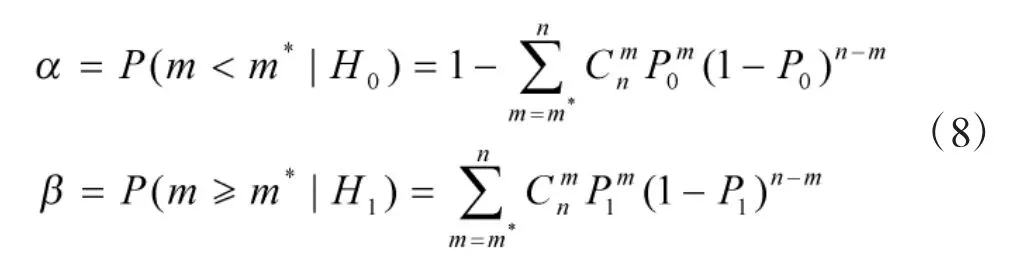
考虑如下鉴定方案：当m≥m*时，接受原假设，即认为此飞行器的落点精度符合要求；否则拒绝原假设，认为此飞行器的落点精度不合格。m*为检验门限。

综合式（7）和式（8）可以看出，当射击准确度、射击密集度和检出比确定后，可以通过调整试验子样m、检验门限m*和概率圆半径R 获得使用方和研制方满意的风险。在实际应用过程中，由于m*是整数，只调整m*时，α 和β 变化剧烈，且m*的变化会直接影响到试验消耗，一般通过调整圆半径R 的大小来确定试验方案。这种通过设计概率圆R 控制双方风险来确定试验方案，从而对圆概率偏差CEP进行检验的方法，即为精度评定中的概率圆方法［3-5］。

2.3 概率圆检验的应用分析

假 设μ0=100、σ0=500，λ=1.5， 则 计 算 得 到CEP0=600 m，总共进行8 次试射。试验方案如表2所示。

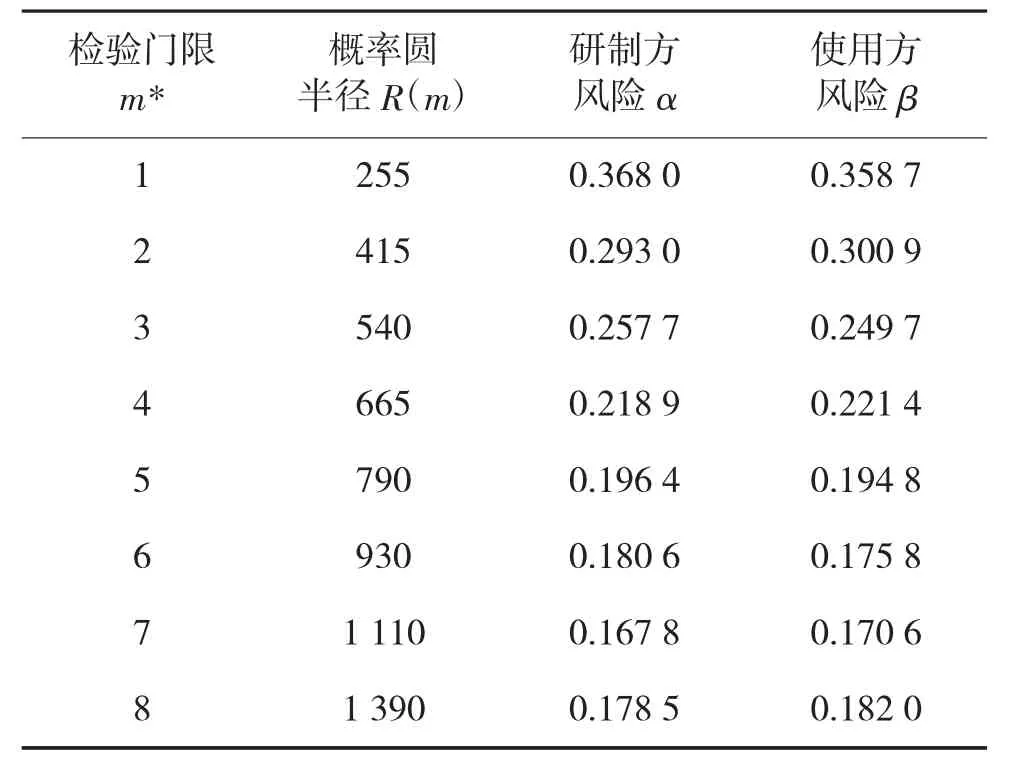
表2 概率圆检验实例

分析表2 可以发现，在射击准确度μ0、射击密集度σ0、检出比λ 和试验样本n 确定的情况下，概率圆方法应用呈现如下特点：

1）确定试验子样n 和检验门限m*后，概率圆半径R 增大，α 减小，β 增大；概率圆半径R 减小，α增大，β 减小。通过调整R 来改变P0、P1，进而改变α、β 使之达到双方可接受的风险，这就是概率圆方法的核心思想；

2）检验门限m*与双方风险α、β 大致成反比关系，说明试验子样越充分，试验作出“弃真”或“采伪”的概率越小。虽然利用概率圆方法在极小子样条件下也可以给出命中精度检验结果，但是这时双方风险是比较高的，即检验结论并不十分可信，检验门限m*不小于n/2 为宜；

3）概率圆半径R 的确定取决于研制方风险和使用方风险，一般来说，建议双方风险控制在0.1～0.3，双方风险接近且研制方风险略低于使用方风险。同时也要具体情况具体分析，概率圆半径R 的确定应该综合考虑试验成本消耗、双方风险接收能力以及被试品实际精度达到水平等因素。

概率圆检验方法不需要待试验结束后才作出统计决策，而是在试验过程中可以作出统计推断。仍以表2 中的检验方案为例，设定检验门限m*=4，则接收条件为R（m），拒绝条件为R（8），具体检验流程图如图1 所示。

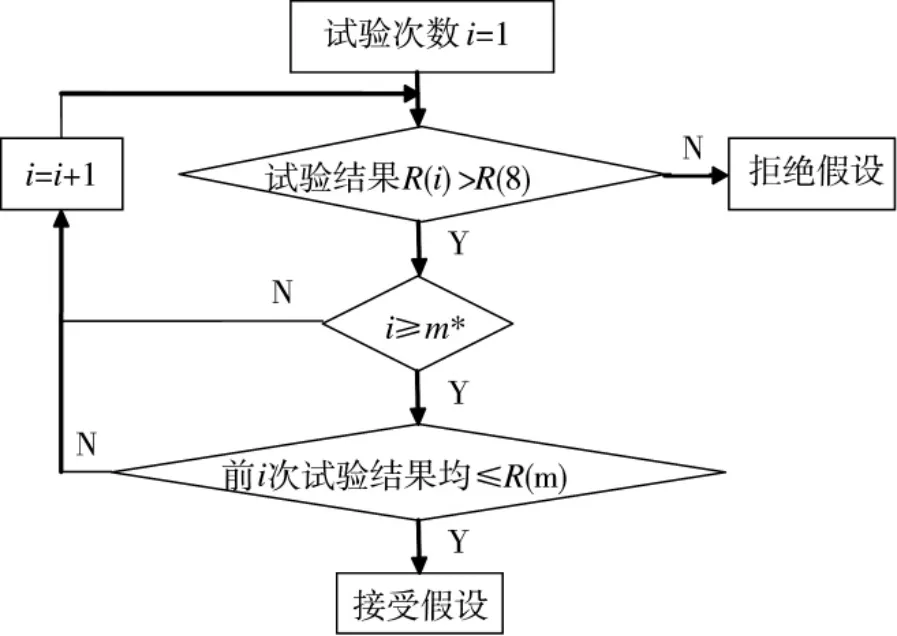
图1 概率圆检验流程图

观察图1 可以发现，最少试验1 次可以给出拒绝假设的结论，最少试验4 次可以给出接受假设的结论，最多试验8 次可以给出接受或拒绝假设的结论，概率圆检验方法蕴含着序贯截尾检验思想［6］。

3 不同母体条件下的概率圆检验方法

试验条件和试验方案的差异都会对命中精度的误差源产生影响，从而导致不同的飞行试验子样的误差成分不一致，也就是说命中精度子样并不属于同一母体，因此，需要对飞行试验子样进行精度折合，将其统一到同一母体，才具备开展精度统计推断的条件。精度折合过程十分复杂，涉及到误差分离、弹道计算、模拟打靶等多项工作，且对计算过程的控制要求十分严格，计算条件的变化会对折合结果产生非常大的影响，因此，精度折合结果很容易引起参试各方的质疑［7-10］。

根据表1 中的对陆攻击飞行器命中精度误差分配情况，可以看出不同风速条件下的试验结果不属于同一母体，在开展精度检验工作前需要对试验结果进行精度折合，需要将每一次飞行试验结果中的风速影响误差分离出来，并折合到最大风速条件下再进行命中精度检验，这项工作建模复杂、过程繁琐，一般很难被检验方技术人员所掌握。概率圆方法为解决不同母体条件下精度检验问题提供了一个新思路，不同试验条件下误差源影响不同，导致命中精度指标有差异，通过概率圆方法可以为不同试验条件构设出不同的检验概率圆，从而将试验结果统一在同一母体中。

仍沿用表1 中给出的误差分配假设：设定试验次数n=8，检验门限m*=4，得到的概率圆检验方法如表3 所示。

利用表3 中给出的概率圆方法可以非常直观地对不同风速条件下的试验结果进行命中精度检验，具体实施步骤可以参照图1 中给出的概率圆检验流程。观察表3 可以看到20 m/s 风速和5 m/s 风速条件下的概率圆半径相差将近一倍，如果不考虑风速影响直接对试验结果进行检验误差是比较大的。这里需要注意的是不同风速下的试验结果对应的检验概率圆需要查表获取，表3 中提供了0 m/s、5 m/s、10 m/s、15 m/s、20 m/s 风速条件下的概率圆半径，其他风速条件下的概率圆半径可以采用就近原则或插值方法得到。

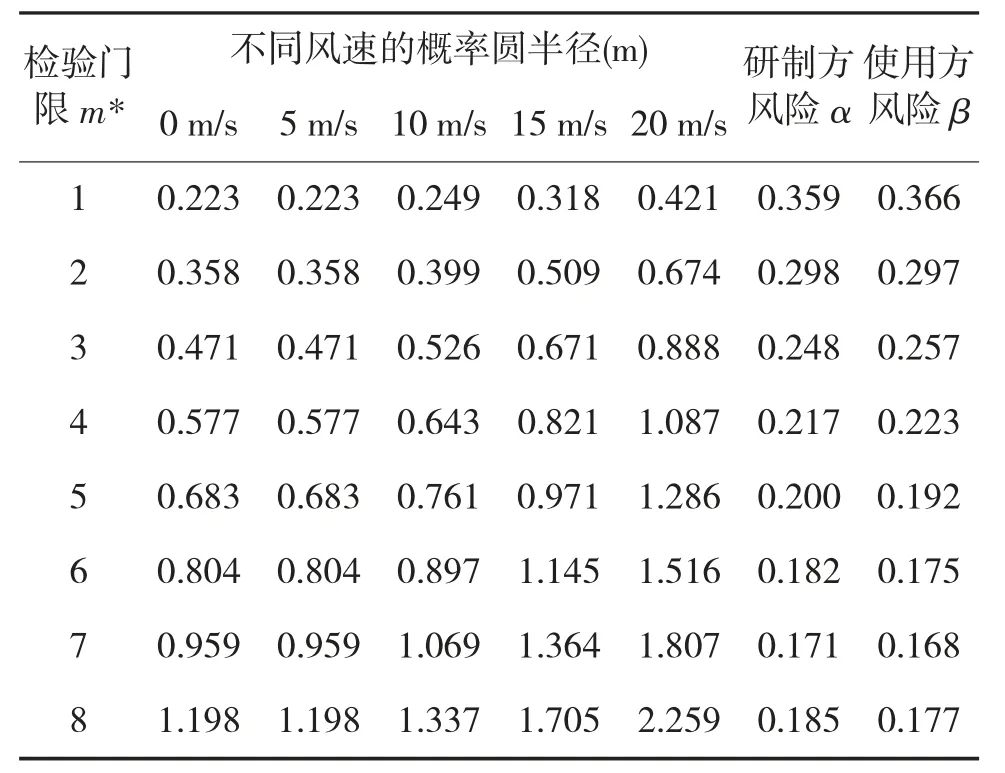
表3 不同风速条件下的概率圆检验方法

4 概率圆检验方法的运用实例

某型对陆攻击飞行器共进行了两个阶段的发射飞行试验，各获取了4 次试验的落点数据，按照2.1 节关于落点坐标系的定义，并进行试验数据的归一化处理，得到试验结果数据如表4 所示。

表4 基于序贯的概率圆检验结果

通过表4 可以观察到风速对于试验结果的影响。采用就近的原则，4 m/s、5 m/s、6 m/s 风速条件下的试验结果使用表3 中5 m/s 的概率圆判据，9 m/s风速条件下的试验结果使用表3 中10 m/s 的概率圆判据，综合表3、表4，可以对试验结果作出如下判断：

1）前4 次试验结果均小于0.577，按照概率圆序贯检验方法，可以得出命中精度指标满足要求的试验结论；

2）后4 次试验结果均小于0.643，按照概率圆序贯检验方法，也可以得出命中精度指标满足要求的试验结论，虽然后4 次试验结果也小于0.577，但要看到0.549 已经十分接近0.577，设置不同风速下的概率圆检验半径是非常有意义的；

3）综合8 次飞行试验结果，5 m/s 风速条件下的概率圆判据与最大试验偏差的比值为3.025，10 m/s风速条件下的概率圆判据与最大试验偏差的比值2.435，可以认为被试装备精度指标水平明显优于设计指标，具体指标达到情况可以使用命中精度估计方法进行估计。

5 结论

本文主要针对对陆攻击飞行器飞行试验中不同风干扰影响下的命中精度检验这一具体问题，提出了应用概率圆检验方法来设计出不同风干扰条件下检验概率圆半径，从而回避了不同母体试验结果的精度折合问题，有效解决了在精度检验工作中使用方不具备精度折合计算条件、研制方精度折合计算结果难以得到参试各方认可的问题。该检验方法基于的数据基础充分易得，理论推导严谨可靠，使用过程简捷高效，为靶场以及研制方进行命中精度检验提供了一套可行的工程应用方法。该方法对于解决验前误差模型确定、试验结果分属不同母体的命中精度检验问题具有较好的推广价值。