穿爆弹侵彻多层间隔混凝土靶数值模拟分析

张斌伟，舒健生，李亚雄，孟少飞，武 健

（火箭军工程大学作战保障学院，西安 710025）

0 引言

穿爆弹穿透混凝土板后的剩余速度决定了弹体的打击深度。剩余速度较大的话，就有足够的动能侵彻进入目标的内部，经过引信的延时后再发生爆炸，可以有效地毁伤目标。因此，有效地预测弹体的剩余速度，可为武器设计和工程防护提供帮助。

弹丸侵彻混凝土靶的研究方法可分为3 种：即经验方法，理论方法和数值模拟方法。由于经验方法具有实用性和可靠性，因此，一直被人们所重视，但是经验方法求解的大多是侵彻深度，侵彻后的剩余速度，难以求解侵彻过程中的速度、加速度等量。为了利用侵深公式得到瞬态量，Young［1］提出了一种近似计算方法，该方法把加速度在弹体冲击每一层混凝土靶过程中看作常量，未考虑靶背崩落的影响，计算精度比较差。韩丽［2］提出了一种“线性加速度模型”计算方法，较好地改善加速度波形，但是求解穿透每层靶板后的剩余速度与实际有较大的误差。许多实验表明［3-4］，弹丸侵彻混凝土目标时，加速度衰减很剧烈，且穿透薄靶板时靶背往往出现崩落现象。因此，本文提出了一种非线性加速度模型来求解穿透每层靶的剩余速度，并考虑靶背崩落的影响。

1 非线性加速度模型

为了用侵深公式求解穿爆弹穿透每层混凝土靶板后的剩余速度，提出了一种非线性加速度模型。假设在第n 层中满足：

式中，a 为加速度，x 为侵彻距离。

积分式（1）可得

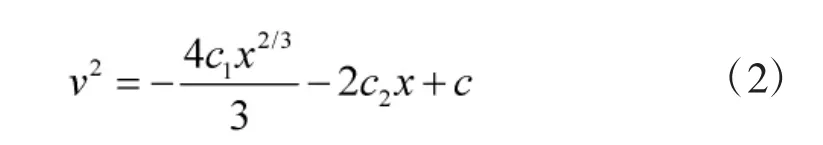
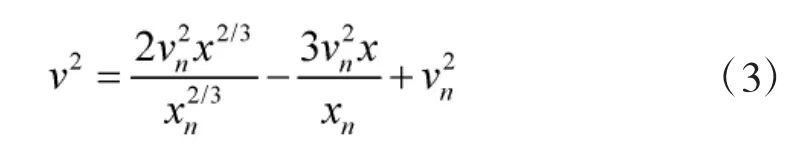
式中，vn为弹体侵彻第n 层时的速度，xn为假定第n层为无限厚时弹体在该层中的侵彻距离。

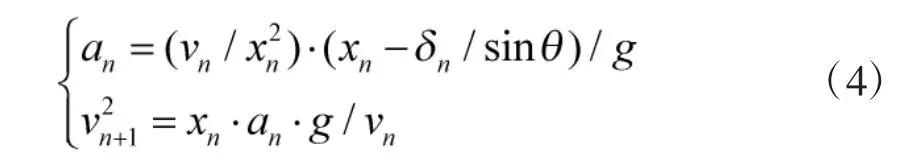
式中，δn为穿爆弹穿透第n 层的有效厚度，根据相关实验结果，δn约为原厚度的0.6 倍［5］。θ 为侵爆弹的入射角，入射角为导弹轴线与入射表面法线的夹角。

2 贯穿多层间隔混凝土薄靶板的计算

为了与Young 氏方法和“线性加速度模型”计算方法进行比较，本文中的计算选用Young 混凝土侵深公式。Young 侵深公式［6］具体如下：

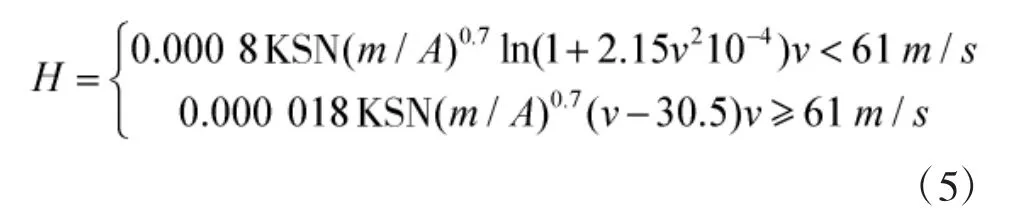
式中，H 为侵彻深度（m）；m 为战斗部质量（kg）；A为弹的截面积（m2）；N 为弹头性能系数，对于卵形弹头

式中，ρ 为弹头部表面曲率半径，D 为弹体横截面直径；S 为混凝土的可侵彻性指标；K 为尺缩效应系数。当m＜182 kg 时，K=0.46m0.15；当m＞182 kg 时，K=1.0。

其中混凝土可侵彻性指标值用下列公式计算：

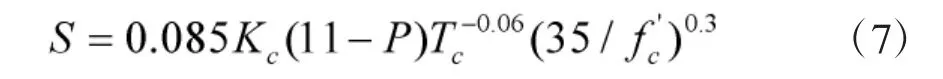
式中，P 为混凝土中钢的体积分数（%）；f 'c为实验时混凝土的无侧限抗压强度（MPa），Kc与混凝土材料有关。在无足够的数据计算混凝土S 值时，建议采用S=0.9。

3 穿爆弹侵彻3 层间隔混凝土靶板数值模拟

计算的基本假设：穿爆弹与混凝土靶板为均匀连续介质，初始应力为零；整个侵彻过程为绝热过程；不计空气阻力的影响，同时不考虑重力的作用。计算软件采用LS-DYNA 程序。LS-DYNA 程序是一款非线性动力分析软件，具有强大数值模拟功能，特别适合求解高速碰撞、爆炸冲击等问题。

3.1 计算模型的建立

战斗部壳体的材料为钢42 SiMn，密度为7.89 g/cm2，采用各向同性弹塑性模型*MAT_PLASTIC_KINEMATIC。本构模型采用Von-Mises 准则，破坏准则采用有效失效准则，即当单元的应变达到临界值时，认为单元破坏。

炸药和引信按原始装药进行处理，炸药采用*MAT_HIGH_EXPLOSIVE_BURN 材料模型，不设置起爆点；引信采用塑形动能*MAT_PLASTIC_KINEMATIC 模型。在数值计算时，为了方便建模，将战斗部内除壳体外的重量全部附加到弹药部分，因此，其密度与炸药的实际密度有所区别。装药和引信的材料参数参考文献［7］。

混凝土材料采用*MAT_JOHNSON_ HOLNQUIST_CONCRETE 模型，又称为H-J-C 模型。该模型主要用于高应变率、大变形下的混凝土和岩石的模拟。其中混凝土的参数根据文献［8］提供的方法来确定。

3.2 垂直侵彻三层间隔混凝土靶数值模拟

3.2.1 有限元模型

战斗部采用球形弹头，3 层靶板厚度分别为30 cm、25 cm、25 cm。考为了节省计算时间，建立三维1/4 模型，如下页图1 所示。在对称面面上施加对称约束，靶板上下界面为自由界面，不施加任何约束，靶板边界施加固定约束。战斗部与靶板之间的接触面采用面- 面接触中的侵蚀算法，单位为cm-g-μs。其中PART1 为壳体，PART2 为装药，PART3、PART4、PART5 为3 层混凝土板。

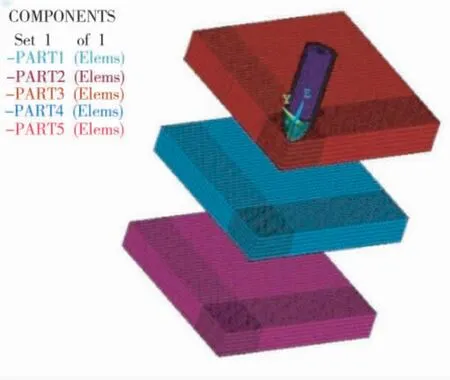
图1 正侵时弹与靶板的有限元模型

3.2.2 侵彻过程分析

图2 给出了内爆式战斗部以800 m/s 的速度侵彻3 层间隔钢筋混凝土靶板在不同时刻的侵彻效果及弹、靶板的变形和破坏情况。

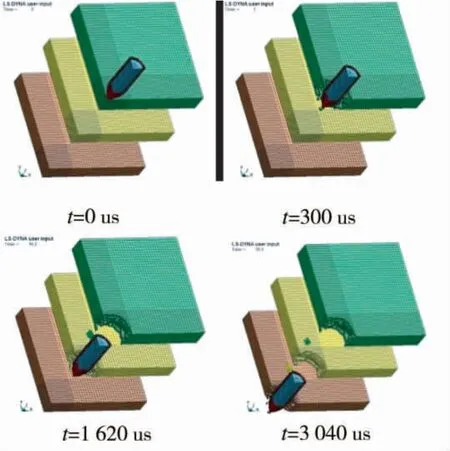
图2 正侵时不同时刻靶板的破坏情况

从图2 中可以看出战斗部穿透靶板过程中对靶板的破坏情况。由于靶板较薄，战斗部对靶板的作用属于冲击贯穿，没有隧道穿孔阶段。而且还可以看到，战斗部穿透靶板飞出时，出现靶背崩落现象，靶板背面部分临空介质随着溅落。

3.2.3 侵彻速度曲线

图3 为战斗部的速度-时间历程曲线，其中A曲线表示战斗部壳体的速度历程曲线，B 曲线为装药部分的速度历程曲线。由速度-时间历程曲线可以看出，战斗部在侵彻3 层钢筋混凝土靶板的过程中，速度有3 次阶梯式下降，主要发生在战斗部对每层靶板的侵彻过程中，而战斗部在空气飞行速度基本没有损失。在战斗部侵彻每层靶板的过程中，开始时战斗部的速度下降比较缓慢，这一段时间正是战斗部开始撞击靶板到弹头侵入靶板的过程。之后到塞块形成这段时间内，速度下降很快，几乎成直线下降。战斗部和塞块一起运动直到弹尖到达靶板背面这段时间，速度下降又相对缓慢。战斗部开始穿出靶板时，速度曲线变化比较剧烈，完全穿出后，速度渐趋平稳，最终以703.3 m/s 的速度穿出靶板。

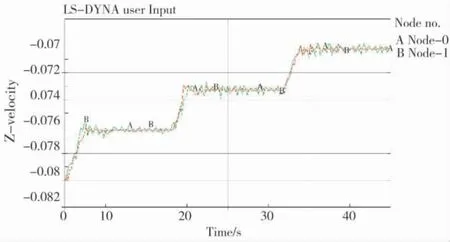
图3 正侵时弹体速度-时间曲线

3.3 着角侵彻三层间隔混凝土靶数值模拟

3.3.1 有限元模型

战斗部以20°着角侵彻3 层间隔钢筋混凝土靶板，靶板厚度与垂直侵彻一样。根据对称性建立三维1/2 模型，如图4 所示。在对称面面上施加对称约束，靶板上下界面为自由界面，不施加任何约束，靶板边界施加固定约束。战斗部与靶板之间的接触面采用面-面接触中的侵蚀算法，单位采用cm-g-us建模。

图4 斜侵时弹与靶板的有限元模型

3.3.2 侵彻过程分析

下页图5 给出了侵爆战斗部以800 m/s 的速度以20°着角侵彻3 层间隔钢筋混凝土靶板在不同时刻的侵彻效果及弹、靶板的变形和破坏情况。

从图5 中可以看出，战斗部穿透靶板后在靶板上形成的弹坑也包括初始弹坑和隧道区，但与垂直侵彻时形成的弹坑有明显的不同。垂直侵彻时，形成正截锥形的弹坑，径向方向上的开坑半径相同；倾斜侵彻时，初始弹坑为斜截锥形。

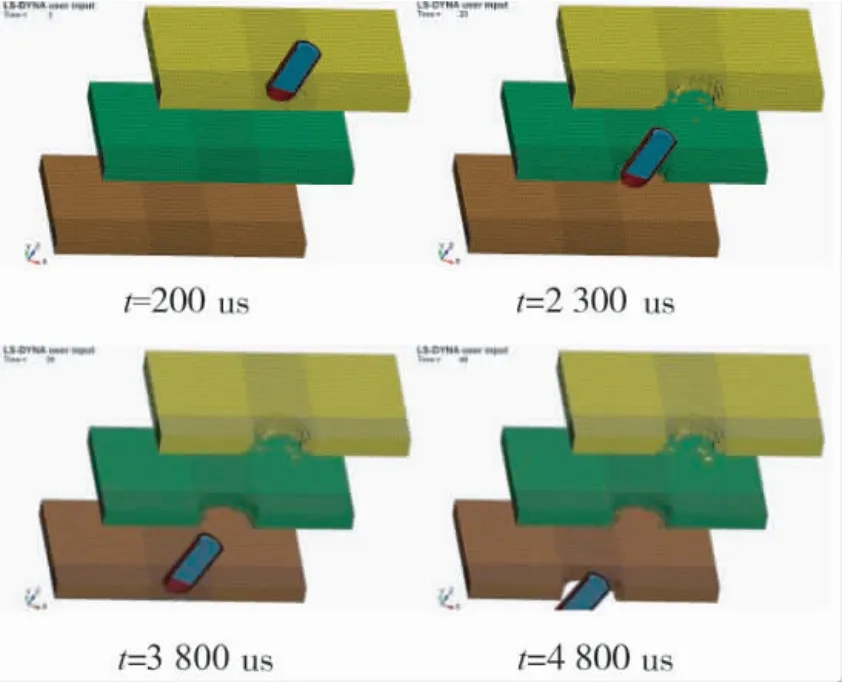
图5 斜侵时不同时刻靶板的破坏情况

3.3.3 侵彻速度曲线

图3～图5 为20°着角条件下战斗部的速度-时间历程曲线，其中A 曲线表示战斗部壳体的速度历程曲线，B 曲线为装药部分的速度历程曲线。由速度-时间历程曲线可以看出，战斗部在20°着角条件下侵彻3 层钢筋混凝土靶板的过程与垂直侵彻过程类似，速度有3 次阶梯式下降，主要发生在战斗部对每层靶板的侵彻过程中，而在空气飞行速度基本没有损失。在战斗部开始撞击靶板时，战斗部的速度下降比较缓慢；在弹头侵入靶板时，塞块开始形成，战斗部的速度迅速下降很快，几乎成直线下降；而战斗部开始穿出靶板时，速度曲线变化比较剧烈，完全穿出后，速度则渐趋平稳，最终以697.2 m/s 的速度穿出靶板。

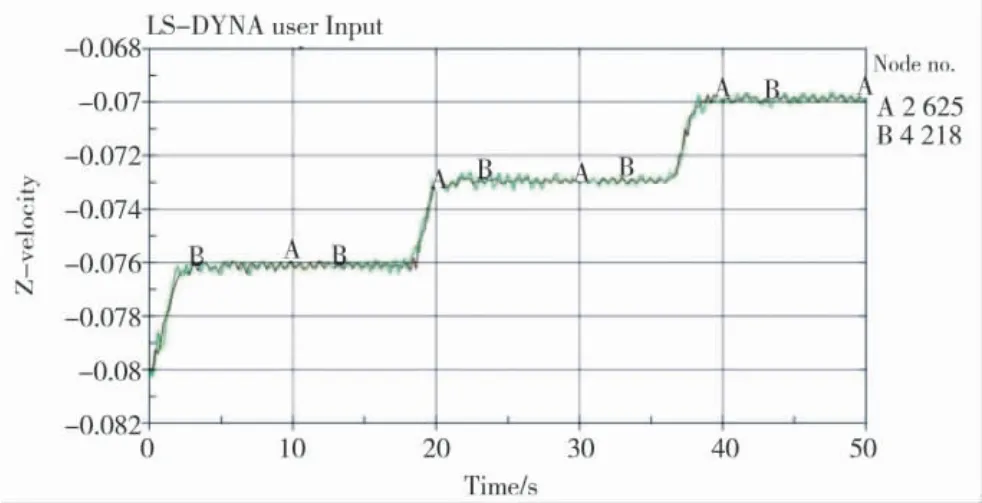
图6 斜侵时弹体速度-时间曲线

4 数值模拟结果及与计算的对比

为了验证本文所提出方法的合理性，首先利用该方法计算穿爆战斗部以800 m/s 的初速度垂直侵彻和以20°着角侵彻3 层间隔混凝土靶板过程中穿透每层靶板后的剩余速度，并与数值模拟结果进行比较。垂直侵彻和以20°着角侵彻的结果对比如表1和表2 所示。

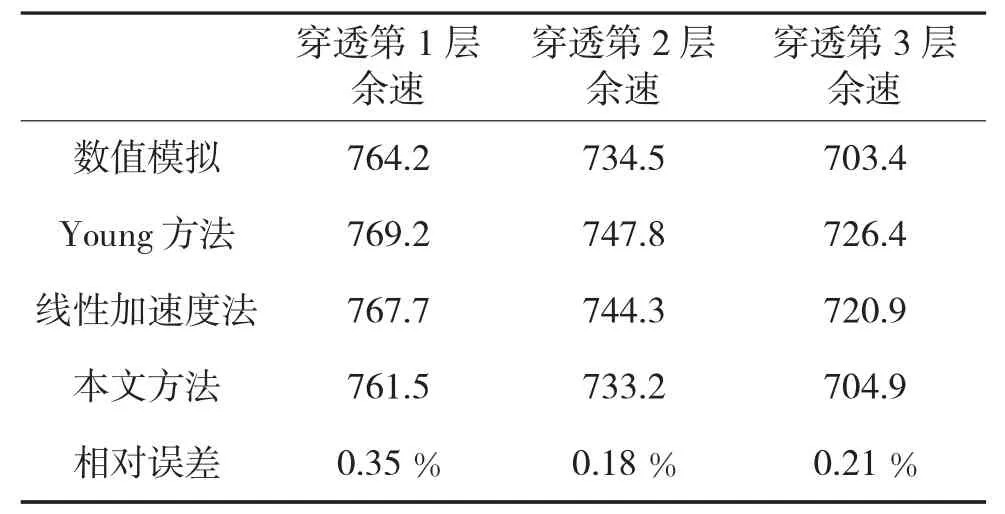
表1 本文方法与数值模拟结果比较（垂直侵彻）

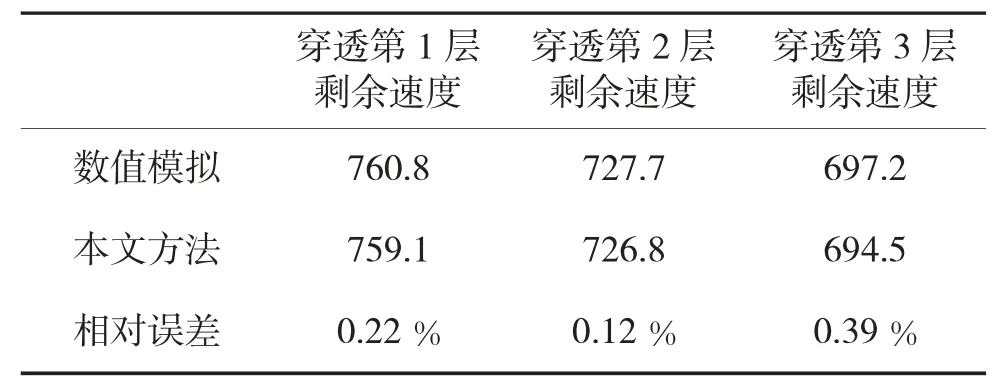
表2 本文方法与数值模拟结果比较（20°着角）

由表可知，无论是垂直侵彻还是倾斜侵彻，利用该方法计算所得结果与数值模拟都具有较好的一致性，验证了本方法的合理性。

为了证明该方法能有效提高计算剩余速度的精度，将文献［9］中的试验值与本文方法、Young 氏方法、线性加速度模型方法及数值模拟结果所得结果进行比较，如表1 所示。

从表1 中可以看出，数值模拟结果与试验值具有较好的一致性，证明本文数值模拟的模型和材料的合理性；Young 氏方法计算结果明显偏大，线性加速度模型相对Young 氏方法结果较小，但对于试验结果来说仍然偏大，而本文的方法则更接近试验值，说明本文方法能很好地减小计算剩余速度的误差。

5 结论

从数值模拟结果与本文方法计算结果的一致性验证了该方法合理性。Young 氏方法虽然也可以计算剩余速度，但由于其设定加速度为常值，致使剩余速度越来越大，误差很大；而线性加速度模型虽然改善了加速度曲线波形，但是计算剩余速度时有较大的误差，而本文的方法则能有效减小计算剩余速度的误差，可以提高计算剩余速度的精度，特别适用于计算弹丸贯穿多层混凝土薄靶板剩余速度的求解。而且还可近似计算弹丸侵彻半无限厚混凝土目标过程中的瞬时量，是一种比较实用的方法。