修正EWMA 控制图在MAP 中的应用

丁宸宇，岳瑞华，李远冬

（火箭军工程大学，西安 710025）

0 引言

导弹测发控系统在导弹地面设备中的重要地位体现在导弹武器系统的设计、生产、实验和实战的整个过程中。测发控设备的技术指标与精度是确保导弹稳定运行的重要保证，因此，必须提高导弹测发控设备的计量与检定水平，从而保证量值传递的准确性与统一性。传统量值传递模式不能有效保证测试发控设备两次检定周期内的准确性和可靠性要求。而新的量值传递方式——计量保证方案（Measurement Assurance Programs，MAP），通过统计过程控制（Statistical Process Control，SPC） 对参加MAP 的所有计量要素进行检定，并确定相对于工作标准的总的测量不确定度［1］。在对导弹测发控设备的MAP 中，由于惯性元素的驱动，样本观测值因相对于时间常数具有较短的采样频率而导致具有时序相关性［2］。然而，传统SPC 中假定连续的样本观测值是相互独立的［3］，这类错误会使控制图对自相关数据非常敏感，即使是非常低水平的自相关也会对控制图产生非常大的影响，导致假警误报率增大［4］。

现行文献在处理数据存在自相关现象，常见有3 种处理方法：1）根据时间序列原理解释过程动态，利用服从独立同分布的残差建立控制图［2］，但是前提条件是残差必须被正确预测；2）对具有时序相关的观测值建立的控制图的控制限进行修改来剔除自相关的影响［5］，但是此类修改只是针对自相关问题，局限较大；3）整合应用控制图，就是将Shewhart 控制图，累积和控制图（CUSUM 控制图）以及指数加权移动平均控制图（EWMA 控制图）综合在一起来解决自相关问题［6］，此类解决问题较为复杂，导致检测过于繁琐。

本文考虑在实际应用中，正常环境下取得的样本数据拟合出的时间序列模型对于中等以上的数据规模来说，其参数估计的误差可能很小，但是其终究不是一个完全独立的残差序列［7］，此时残差即使不独立，也只是存在前后相关。因此，本文考虑将原本用来解决自相关的方法2）用在残差控制图中，用来解决自相关参数估计不足的问题。并以MAP 中得到的数据来验证上述方法的监控效果。

1 测发控系统统计质量控制

MAP 采用的是现代生产中质量管理的思想，并结合控制论和数理统计的相关理论及时发现故障，解决问题。在随后的几十年将受到各国广泛认同，并制定规范推广使用。

1.1 MAP 基本过程

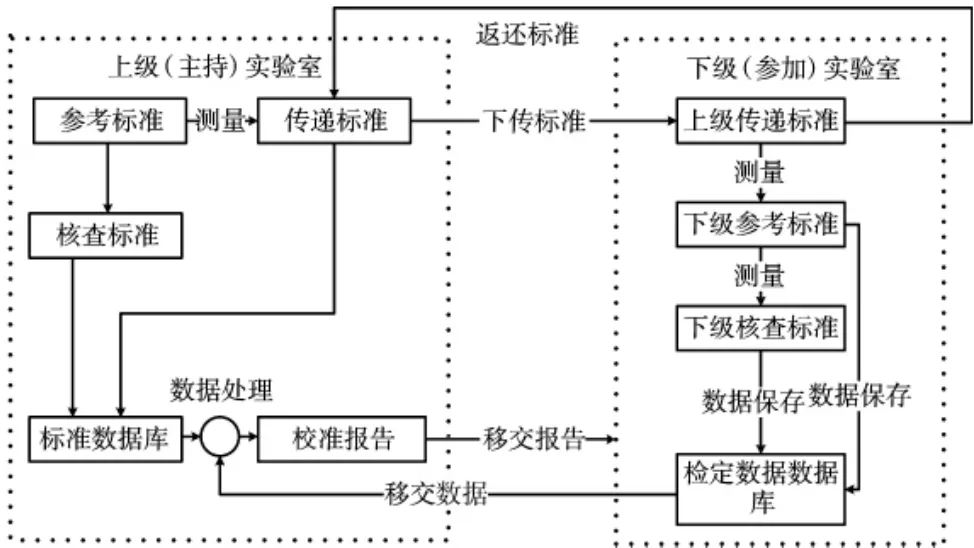
图1 MAP 标准程序框图

简单来说，MAP 主要有闭环量值传递和过程统计控制两部分组成，在量值传递中主要包括传递过程和核查过程［8］。其具体操作如图1 所示。

1.2 统计数据

在对某型号导弹的MAP 过程中，以等效器作为其核查标准，选择数字多用表Keithley 2000 作为其传递标准，对其中一个标准电压源，每隔两小时进行一次抽样检定，每天检测8 h，连续检测得到200个数据。其自相关函数图（ACF）如图2 所示。ACF 显示在4 阶以后自相关系数才收敛到两倍标准差以内，表明样本数据有自相关性。

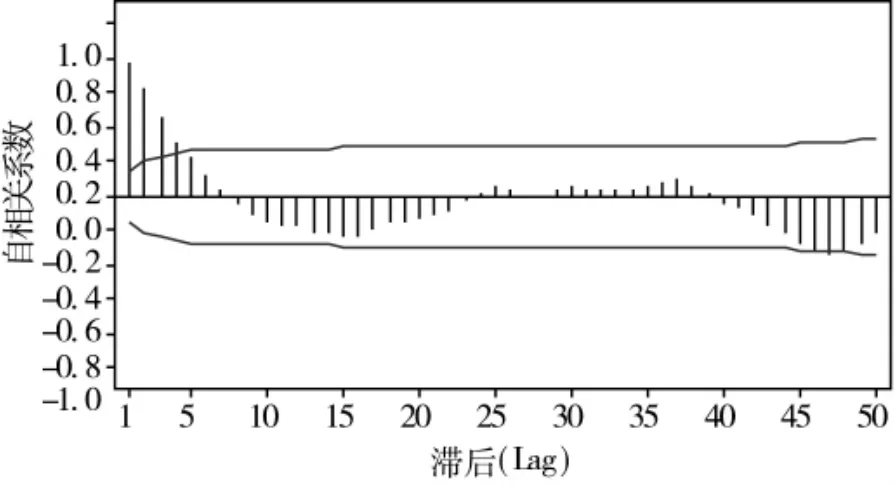
图2 样本数据自相关函数图

2 EWMA 控制图

EWMA 控制图是由Roberts［9］最先提出，可以监视整个输出过程的历史数据，相对于其他只单独处理合理数据分组的方法来说显得更为合理。

2.1 常规EWMA 控制图

EWMA 统计量Yt通常被定义为：

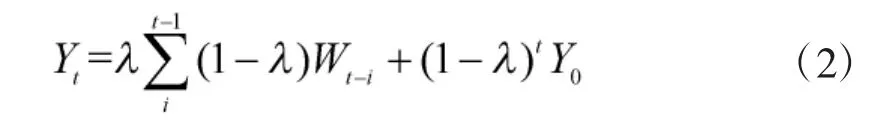
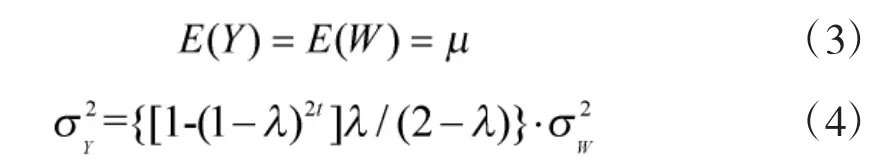
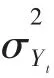
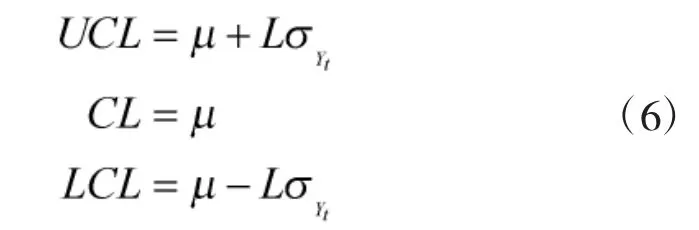
式中，L 为控制限参数，一般大小取3。

2.2 自相关对控制图的影响

在本小结中考虑基于AR（1）模型来处理样本数据的自相关，然后使用修正后的EWMA 控制图来解决自相关问题。平稳AR（1）模型定义为：

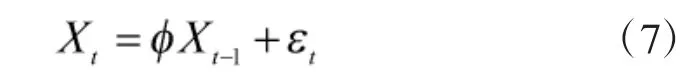
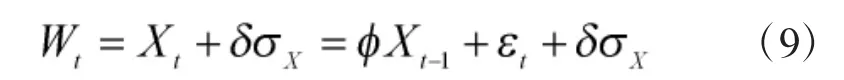
表1 基于AR（1）模型的不同参数的ARL0

2.3 残差控制图

观察式（10）可以发现，此时εt完全等同于残差et，则基于残差的EWMA 控制图统计量可以定义为式（11）：

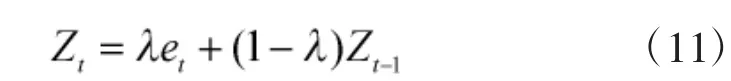
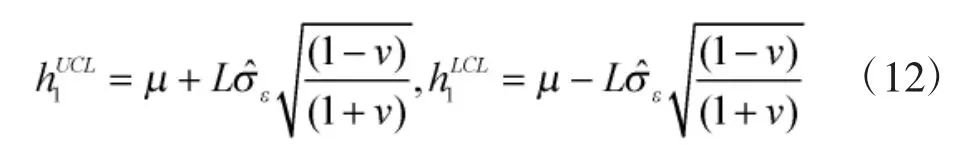
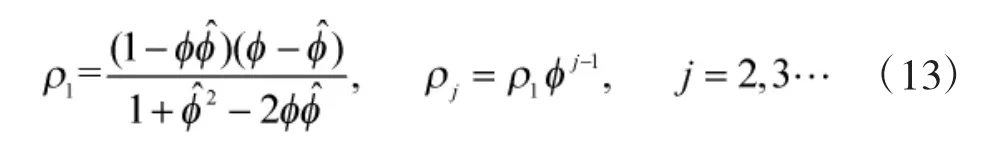
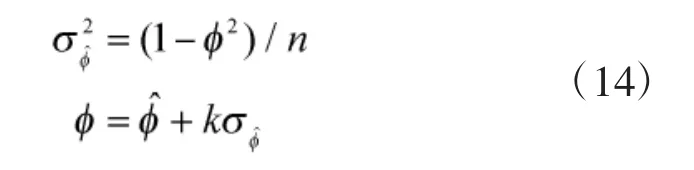
其中，k 可以为-1，-0.5，0，0.5，1。由式（10）可以推得模型估计准确，但是参数存在误差的情况下，预测的误差为：

联合式（11）、式（15），则EWMA 的残差统计量Zt可以表示成：

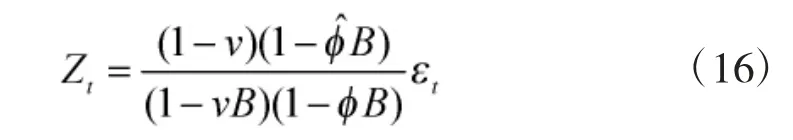
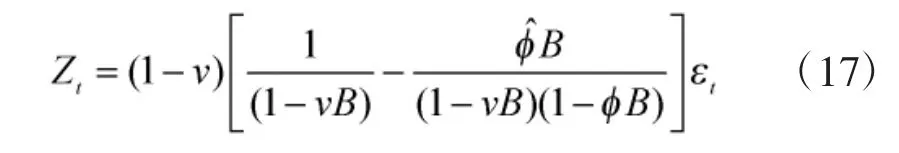
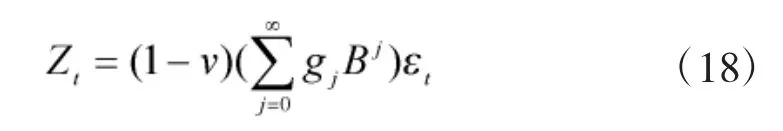
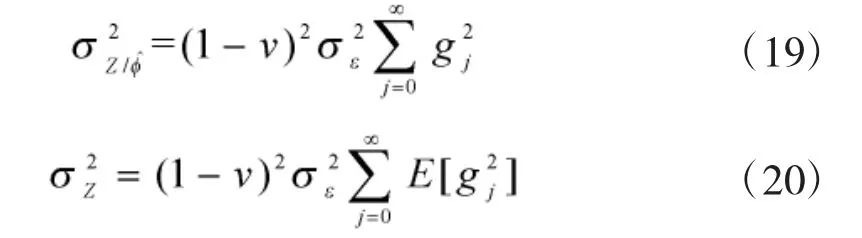
数学抽象是指通过对数量关系与空间形式的抽象，得到数学研究对象的素养．主要包括：从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关联，从事物的具体背景中抽象出一般规律和结构，并用数学语言予以表征[5]．在全国I卷中，有多个题目考查学生的数学抽象素养，以理科15题为例．

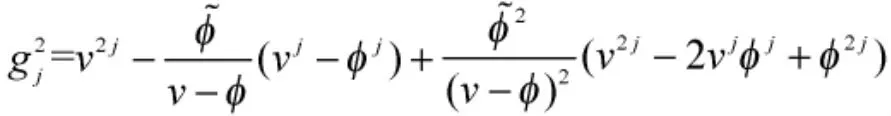
针对此类截断正态分布［9］，有：

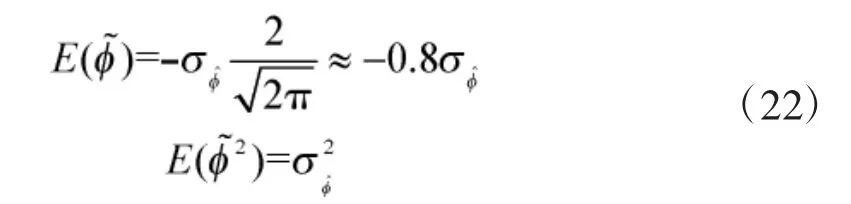
结合式（13）、式（16）、式（21）最终得到其改进后的方差为：

则改进后的控制限±h2为：

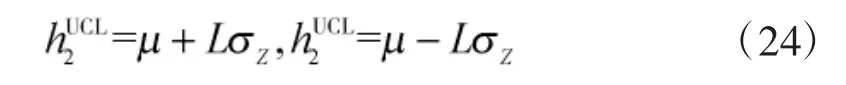
2.4 残差控制图ARL

观察下页表2、表3 两个表格，可以发现：均值发生漂移后，两种控制限的ARL0趋近一致，表明修改后的控制限对均值漂移后的影响有限；在均值未发生漂移，EWMA2控制限的ARL0明显大于EWMA1控制限的ARL0，表明控制图不会因为控制限过窄而导致假警频生；另外自相关参数越高，均值未漂移的EWMA1的ARL0与EWMA2的差值越来越大，表明控制图对自相关数据的处理越来越好。综合以上各点，改进后的控制限明显好于常规控制限。

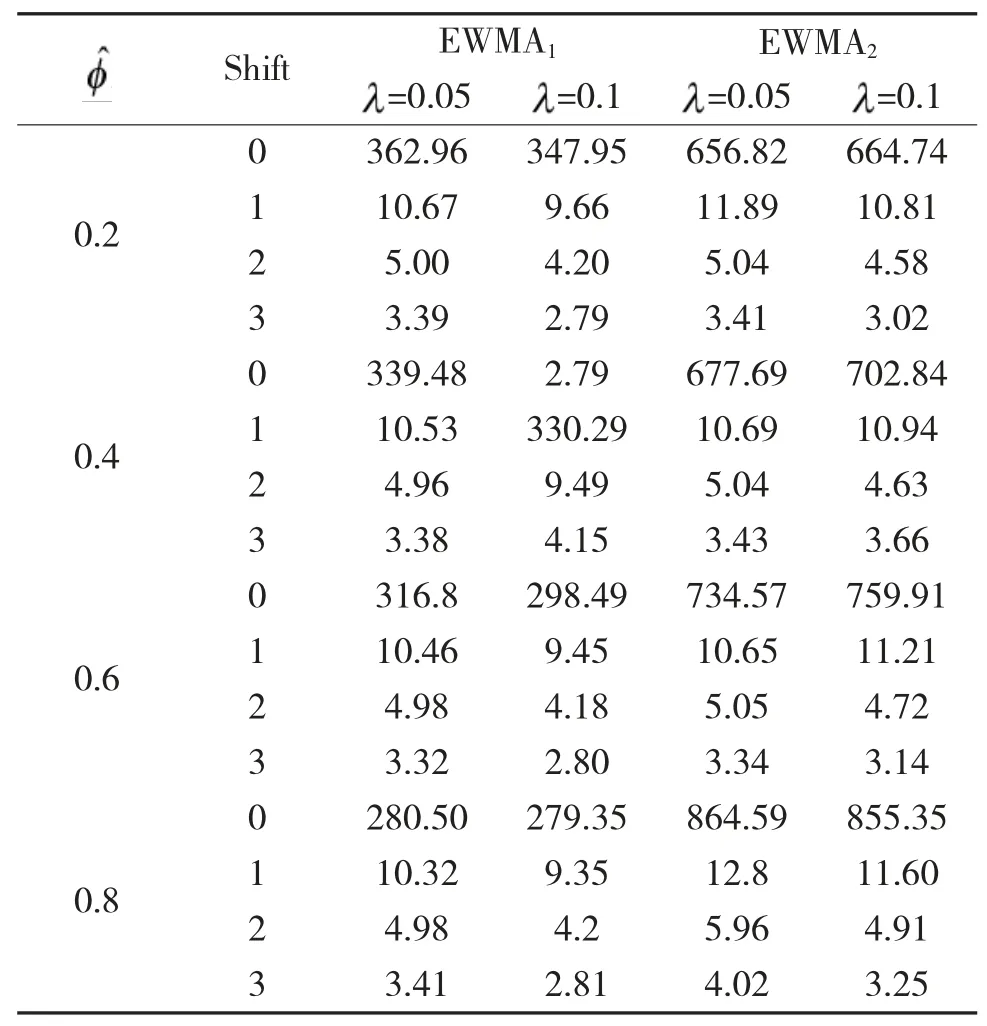
表2 基于AR（1）模型的不同参数残差的ARL0（k=0.5）

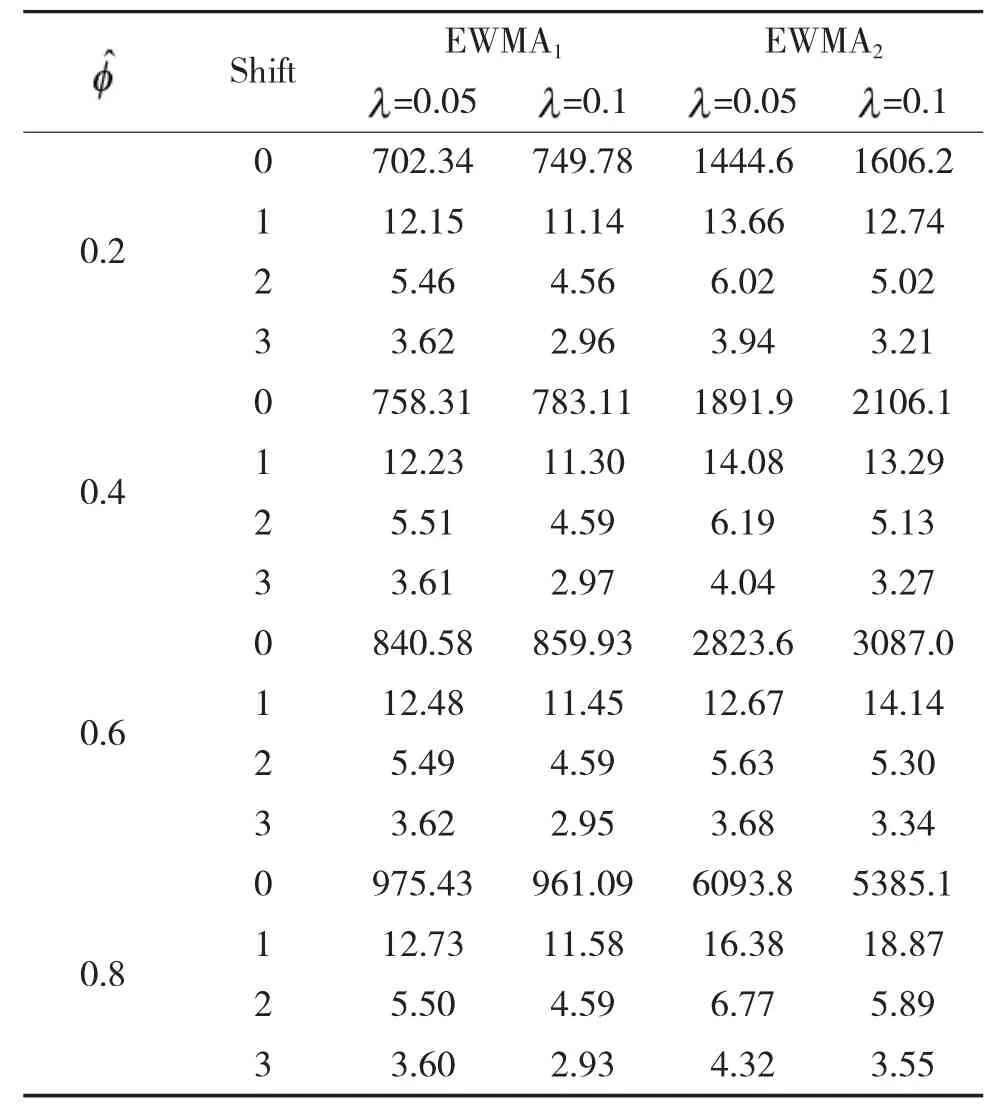
表3 基于AR（1）模型的不同参数残差的ARL0（k=-0.5）

3 实例分析

针对MAP 中已经获得的200 个受控数据，本小结作如下处理：

3）利用步骤1 拟合出的模型计算出余下100个数据的残差。

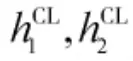
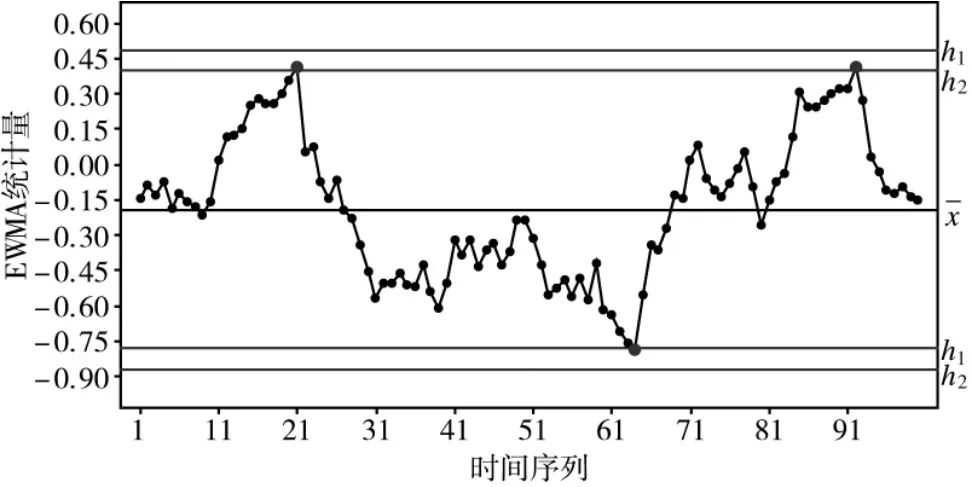
图3 具有不同控制限的残差EWMA 控制图

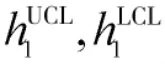
4 结论

针对MAP 中数据存在自相关问题，现阶段较为广泛使用的是在理论情况下独立的残差控制图，但是因为拟合的模型参数不可能完全正确导致控制图的决策出现错误。本文在AR（1）模型下，选用EWMA 控制图计算残差，针对模型参数拟合不足的情况，提出对EWMA 控制图进行修改以抵消参数拟合不足的现象。通过计算修改后的控制限ARL0以及绘制EWMA 控制图进行比较，进一步说明了修改控制限后的控制图性能优异，基本消除了自相关以及参数估计不足导致的虚假警报问题。本文只是对单一统计量的自相关问题进行研究，因此，下一步研究的重点是对多元数据的自相关问题的解决。