改变系统结构的多环姿态跟踪控制*

殷春武，佟 威，何 波

（西安建筑科技大学信息与控制工程学院，西安 710055）

0 引言

捕获并清除严重威胁航天器安全的空间碎片，是当前空间在轨服务中的主要任务，保证抓捕航天器的姿态稳定，是实现在轨捕获诸如空间碎片这类非合作目标的前提。在轨捕获未知范围内非合作目标的过程中，抓捕航天器的机械臂伸展会引起航天器质心位置改变，导致航天器的姿态和转动惯量发生改变；非合作目标的未知性，也导致航天器转动惯量的摄动量未知［1］，因此，研究存在未知转动惯量摄动的姿态跟踪控制，对提升空间轨服务质量和技术具有重要意义。

对存在转动惯量摄动的姿态跟踪控制问题，学者提出了很多控制策略，但主要分为两类：一类是假设转动惯量摄动上界已知，PID 控制、反演控制［2］、滑模控制［3-4］等非线性方法被用来设计姿态跟踪控制器。另一类是转动惯量摄动上界未知，自适应控制或智能控制方法被用来估计未知转动惯量，并结合其他非线性控制方法以保证姿态的稳定［6-7］。现有的非线性姿态跟踪控制方法，虽然解决了转动惯量摄动上界未知条件下，航天器的姿态跟踪控制问题，但姿态跟踪普遍存在稳态误差，使得姿态跟踪精度不高。减小和消除姿态跟踪稳态误差，提高航天器的姿态跟踪精度，已成为当前航天器姿态跟踪控制的主要需求。

滑模变结构控制通过改变控制器结构的控制方法使不可控系统变为可控系统，且增强了被控系统的鲁棒性，说明改变系统或控制器结构的控制方法能有效改善被控系统的品质。以改变控制器结构的滑模变结构控制器，在实际工程中取得较好的应用效果，但通过改变系统结构来提升控制品质的研究成果并不多见。为了提升航天器的姿态跟踪精度，减小和消除姿态跟踪的稳态误差，本文将尝试通过改变姿态动力学的系统结构来实现该目的。

1 航天器姿态控制系统

刚体航天器按yaw-pitch-roll（θ3-θ2-θ1）旋转，则航天器姿态动力学方程（Kinematics）为［4］：

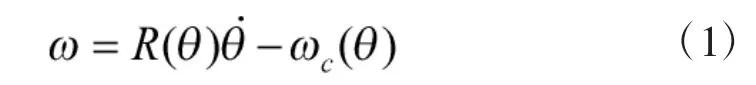
航天器运动学（Dynamics）方程：

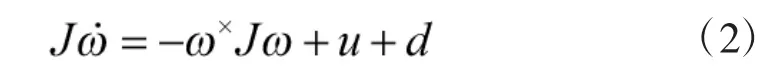
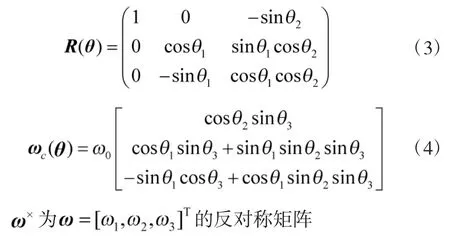
设航天器的期望姿态为θd，期望角速度为ωd，期望角加速度为ω˙d。

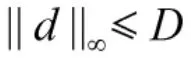
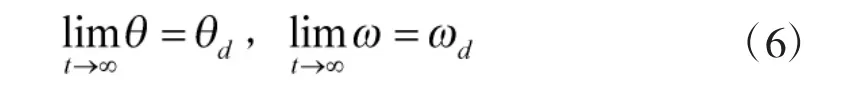
假设1：航天器的姿态角和角速度信息可测。

姿态跟踪控制器均是基于航天器姿态跟踪误差微分方程设计的，最终要求姿态跟踪误差和角速度跟踪误差为零，因此，假设2 是合理的。

2 航天器姿态控制器设计

2.1 航天器扩展姿态控制系统构造

跟踪误差的积分项能有效消除稳态误差，提升姿态跟着精度。令

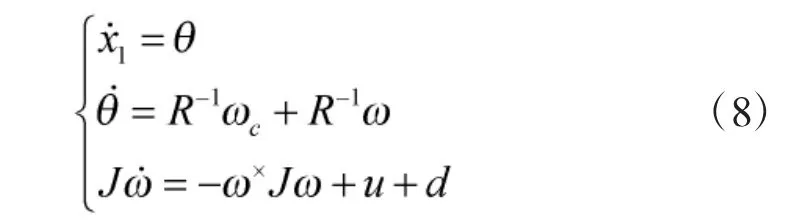
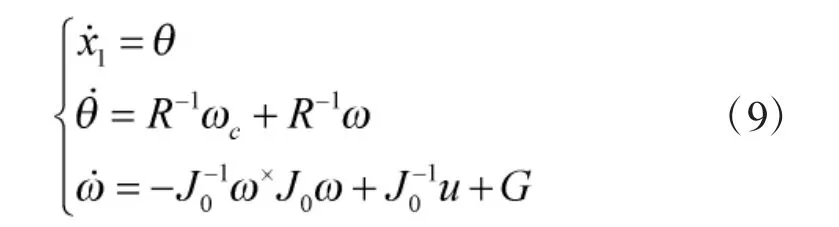
2.2 扩展姿态控制系统的控制目标设置

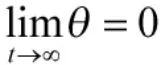
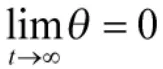
根据上面的分析，三阶扩展姿态动力学系统式（9）的控制目标变为：

2.3 多环递归姿态跟踪控制器设计

针对扩展姿态动力学系统式（9），本文将采用多环递归跟踪控制策略，设计一种多环递归姿态跟踪控制器。多环递归姿态跟踪控制控制结构图如图1 所示。

图1 扩展姿态动力学系统的多环姿态跟踪控制器结构图

设计扩展跟踪器为

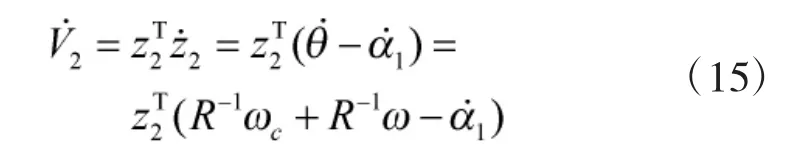
设计姿态角跟踪控制器为

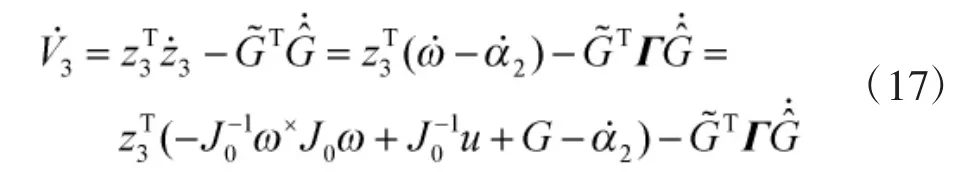
设计角速度跟踪控制器（即多环姿态跟踪控制器，Multi-LoopAttitudeTrackingController，MLATC）为

根据上面的分析，可得到如下定理。

定理1：对扩展姿态动力学系统式（9），其控制器取式（18），自适应控制器取式（19），则闭环系统渐近稳定。即

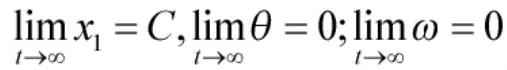
本文设置如下的时变增益函数调整控制器式（18）中的增益系数［8］

3 仿真验证

某航天器的初始转动惯量为J0，转动惯量的摄动量ΔJ 为：

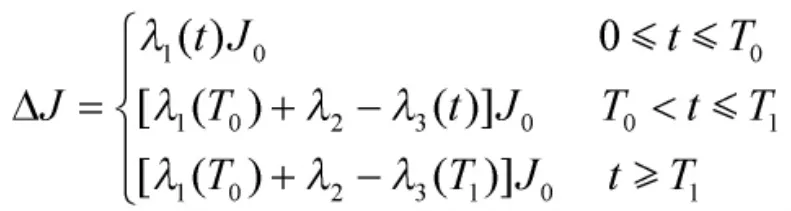
选择文献［9］中的滑模自适应姿态控制器（SAAC）与本文多环姿态跟踪控制器（MLATC）及进行对比仿真，仿真参数见表1，仿真时间80 s，仿真结果如图2 至下页图5 所示。

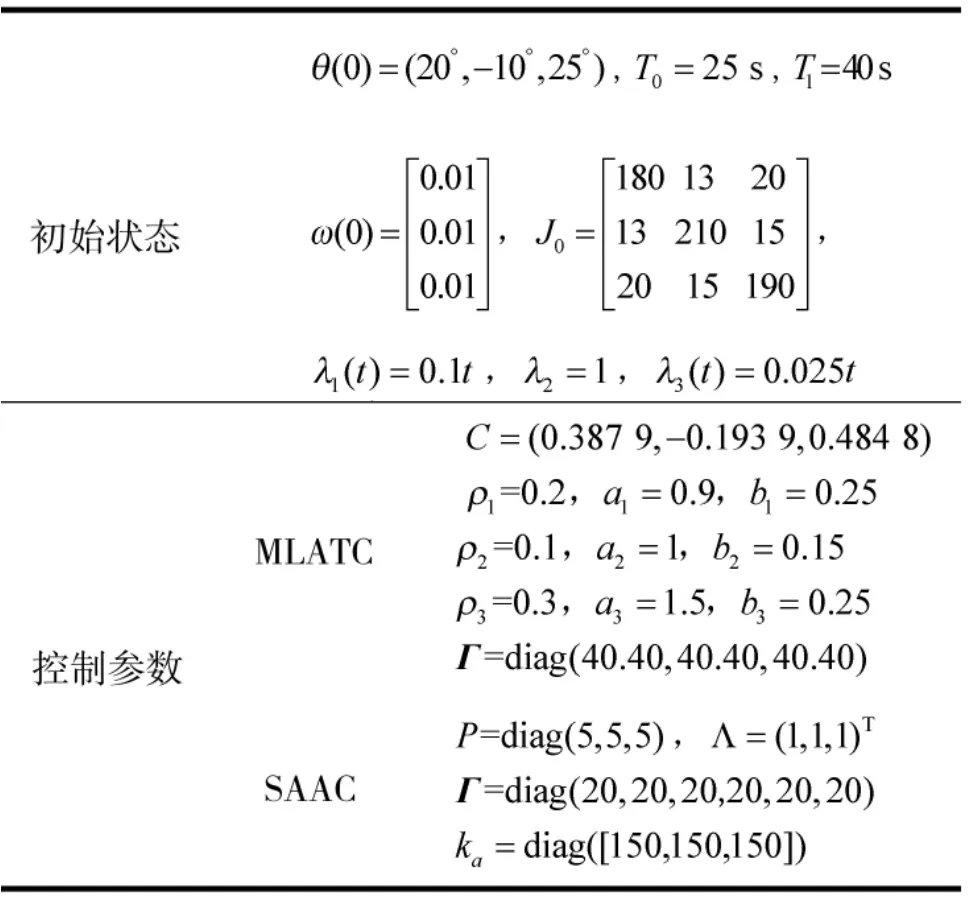
表1 仿真参数表

仿真结果显示：

1）多环递归跟踪控制器能有效实现航天器姿态跟踪控制目的，验证了本文算法在姿态跟踪控制器设计中的合理性和可行性。

2）采用MLATC 时，航天器姿态角的最大稳态误差为0.04 deg，采用SAAC 时，最大稳态误差为0.23 deg，本文设计的MLATC 比SAAC 的姿态跟踪精度高82.6%，有效提升了姿态跟踪精度。

3）与SAAC 控制器相比，采用MLATC 控制器时，航天器姿态收敛的品质更优。控制器为MLATC时，航天器的姿态角呈指数下降，姿态收敛轨迹较为平缓，收敛过程中，姿态仅有1 次俯仰交换；控制器为SAAC 时，航天器的姿态收敛轨迹变化迅速，且整个控制过程中，姿态收敛轨迹至少出现6 次俯仰交换。

4）控制器采用MLATC 时，航天器的最大角速度更小。MLATC 控制下，航天器的最大角速度为0.12 rad/s，当控制器为SAAC 时，航天器的最大角速度为0.46 rad/s，几乎为MLATC 控制下的4 倍，且SAAC 控制下，航天器角速度方向也存在多次振荡变化。

5）航天器采用控制器MLATC 比采用SAAC时，需要的控制力矩更小。MLATC 控制器下，航天器的最大输入力矩为8.5 N.m，而采用SAAC 控制器下，航天器的最大输入力矩超过150 N.m，对于小航天器，根本不可能提供如此大的控制能量。

图2 多环姿态跟踪器下的积分项变化轨迹

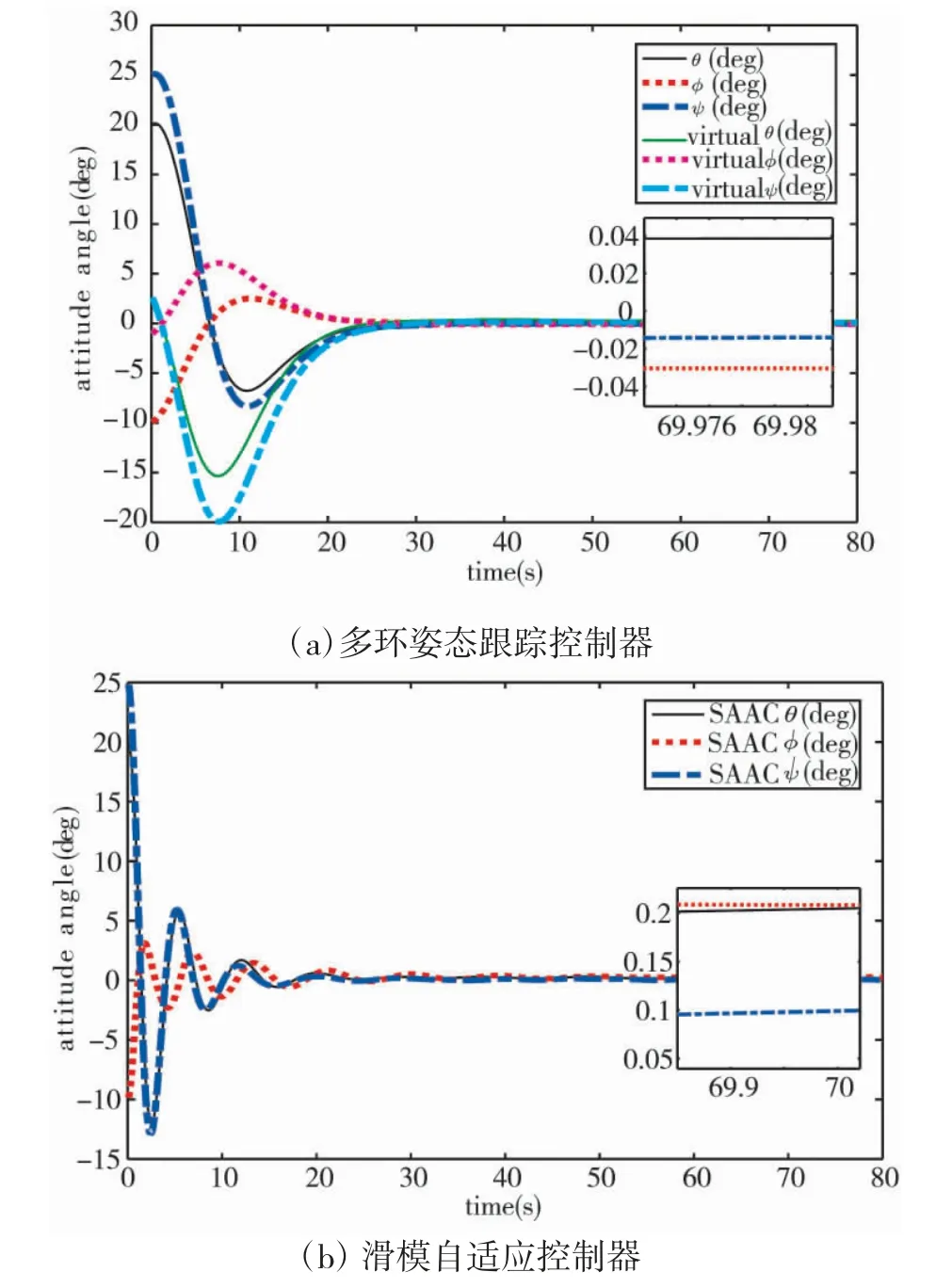
图3 姿态角跟踪曲线

4 结论

为减小姿态跟踪控制中的稳态误差，有效提升航天器姿态跟踪精度，本文提出一种新的姿态跟踪控制策略。通过系统结构调整的方式，将姿态跟踪误差的积分项，引入到姿态跟踪控制器中，以提升姿态跟踪精度。将二阶姿态动力学系统扩展成三阶动力学系统，并给出了新系统的跟踪控制目标和多环递归姿态跟踪控制策略。

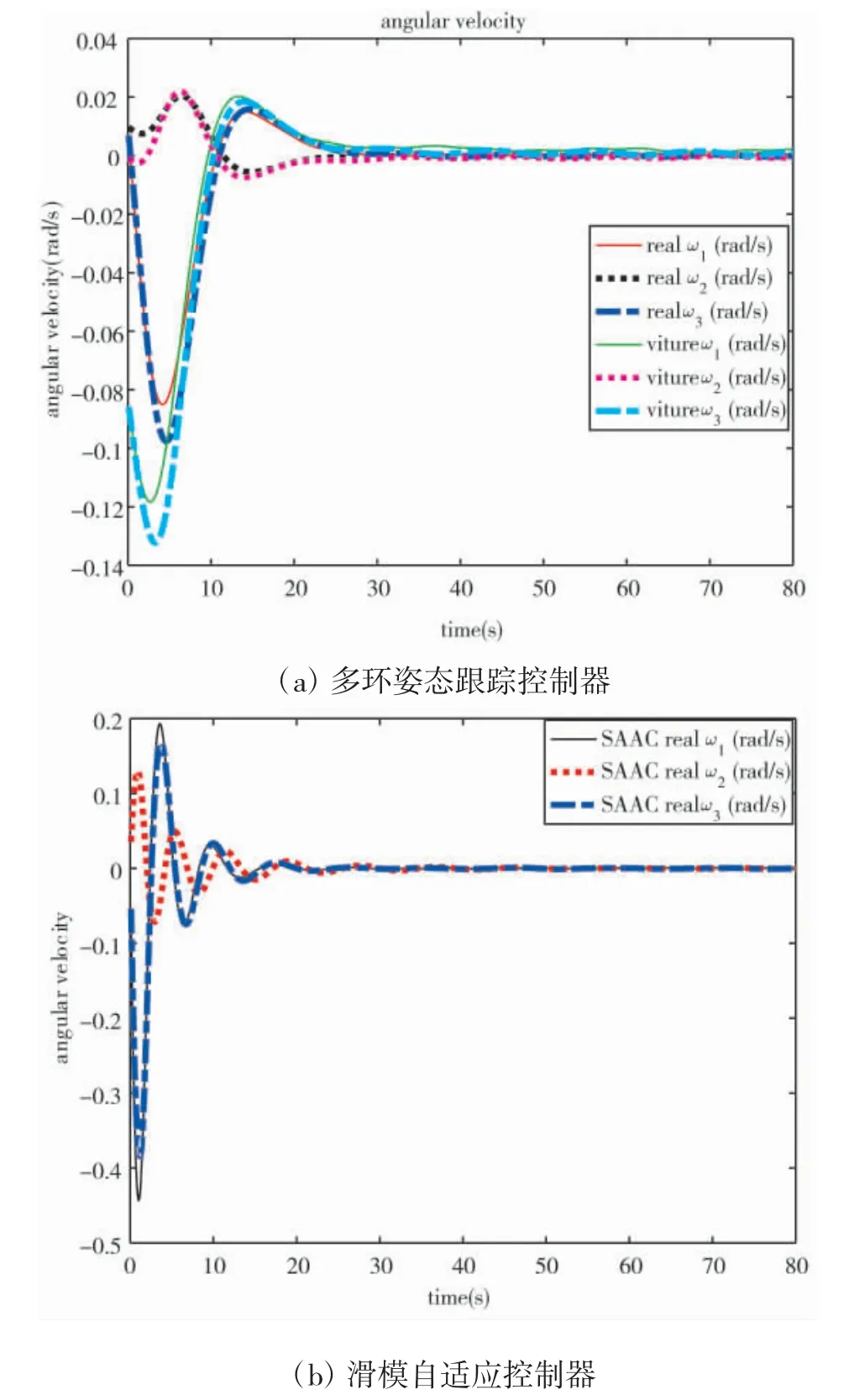
图4 角速度变化曲线

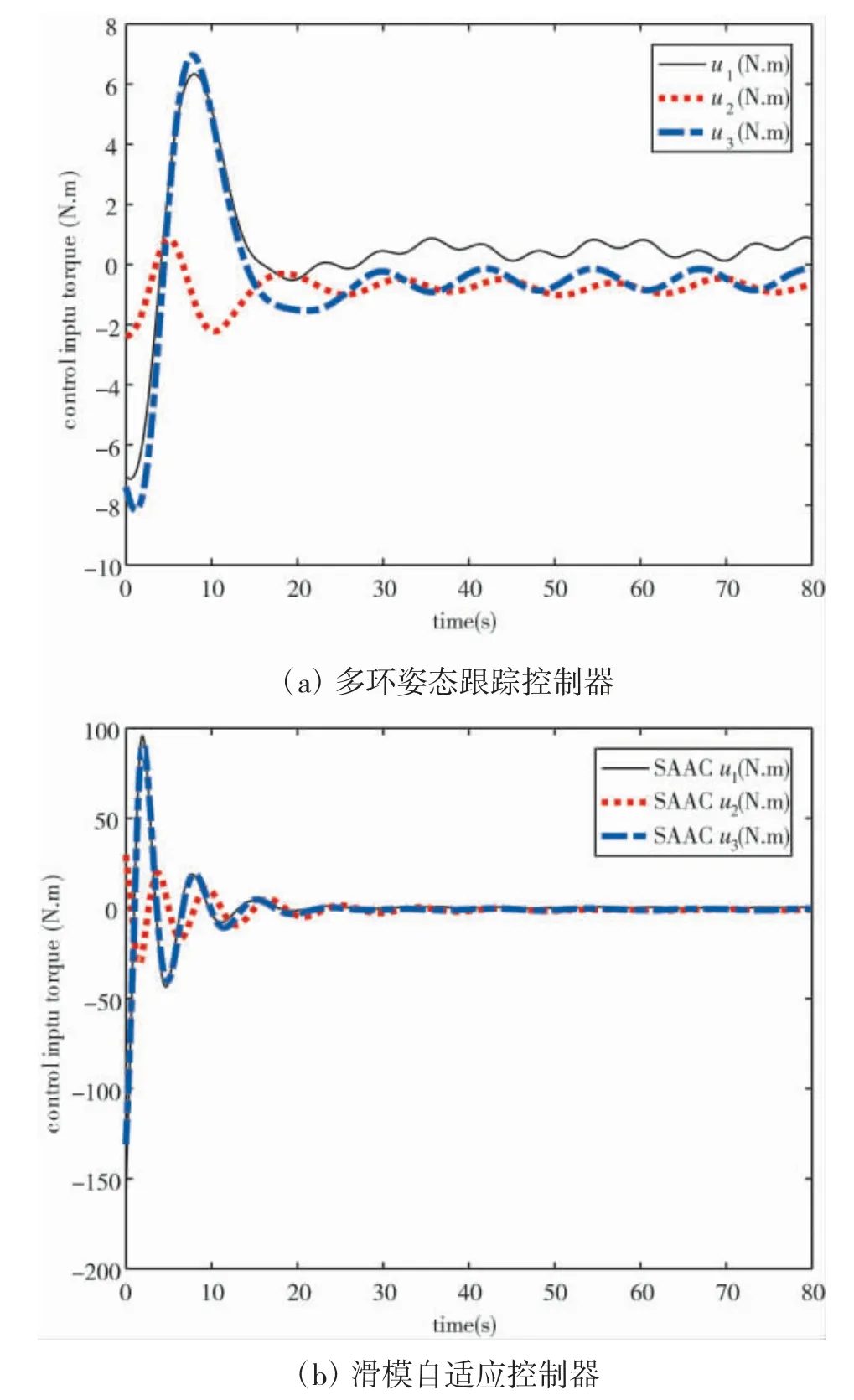
图5 控制力矩变化曲线