基于半定规划的无源跟踪最佳传感器选择*

蔡立平，左 燕*，王文光

（1.杭州电子科技大学自动化学院，杭州 310018；2.北京航空航天大学电子信息工程学院，北京 100191）

0 引言

相比有源定位系统，无源定位系统具有不主动发射电磁信号、生存能力强、隐蔽性能好、探测作用距离远等重要优点，近几十年来受到国内外相关学者和工程技术人员的广泛关注和深入研究［1-2］。多站无源定位系统通过多个观测值获取更多的量测信息，通过多站协同提高目标定位精度［3］。由于许多被动式传感器（如红外、声呐等）都只能得到角度信息，研究基于角度信息的无源协同定位跟踪具有实际意义。

基于角度信息的定位系统目标估计误差与目标和传感器之间的几何关系相关，在接收站量测噪声的概率分布相同的情况下，适当选择不同位置的传感器可以提高系统对目标的跟踪性能。王国刚［4］在忽略地球曲率及两观测站指向误差，假定目标到基线的距离一定且基线与X 轴平行的情况下，推导了二维空间相对误差几何稀释度（GDOP）的具体表达式，得出了GDOP 与传感器精度及其布站方式有关。Levanon［5］给出了二维空间特殊情况下的最优布站，即当目标位于正n 边形的中心时，多站位于正n边形的顶点。修建娟［6］重点研究了二维空间的交会角，推导了基线长度一定时最优交会角，给出了目标速度较慢的情况下的最优布站条件。徐国训［7］针对接收站到目标距离恒定和角度恒定两种情况，将Fish 信息矩阵（FIM）行列式最大作为指标进行了分析，给出了二维空间中四站及以下的最优构型，并给出了两站和三站在各站到目标距离相同的限制条件下的角度关系的解析解。

上述研究主要集中在二维空间，得到的几何分析用于指导传感器静态布站。本文从基于角度信息的无源定位系统协同跟踪性能的角度出发，推导三维空间下目标的CRLB，分析CRLB 指标与传感器和目标之间关系。以CRLB 行列式最大值为优化指标，考虑传感器自身的探测能力等实际约束，基于目标状态的一步预测动态选择最佳传感器组合进行协同跟踪。采用SDP 的方法将上述组合优化问题转换为凸优化问题，进行优化求解，仿真结果验证了算法的有效性［8-10］。

1 问题描述

假设M 个被动传感器组成的阵列对P 个机动目标进行定位跟踪，利用多站纯角度（AOA，Angel of Arrival）量测值估计三维空间内的机动目标的状态（位置、速度）。为满足基于AOA 的多站被动跟踪问题的可观测性，至少需要保证两个及以上的被动传感器跟踪一个目标。每一时刻，从M 个被动传感器中动态选择m 个最佳传感器对每个机动目标进行定位跟踪（m≥2，且m 值受融合处理中心传输通信信道的制约），提高目标的跟踪性能（如图1 所示）。

1.1 运动模型

由于目标是机动的，不能用一个固定的模型来描述目标的运动特性。通常可以把机动目标的运动近似为多个模型的组合，如匀速（CV）模型、匀加速（CA）模型、匀角速度转弯（CT）模型、Singer 模型、当前统计模型等。

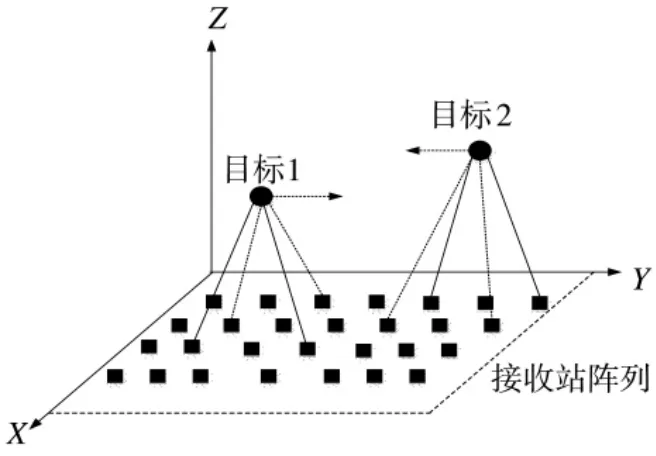
图1 多站被动传感器协同定位跟踪

k 时刻每个机动目标t 的运动方程可描述为

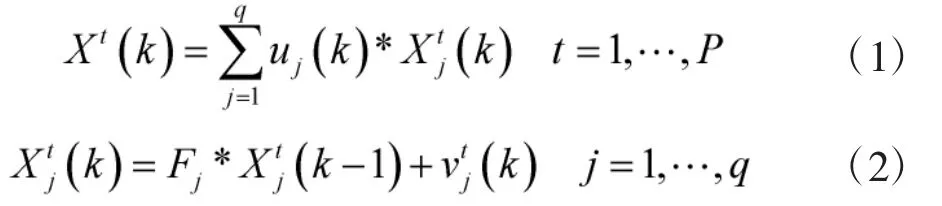
1.2 量测模型

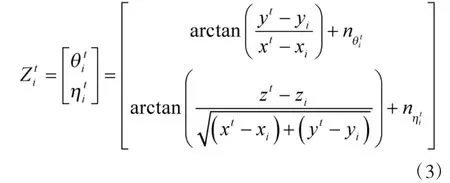
2 纯角度量测参数估计下CRLB

目标跟踪定位的性能通常用CRLB 或者FIM（与误差椭球相关）来进行评估，基于AOA 多站被动跟踪下对目标t 估计的CRLB 可写为

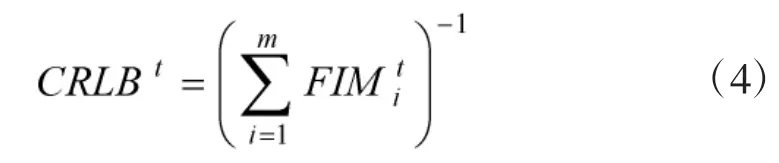
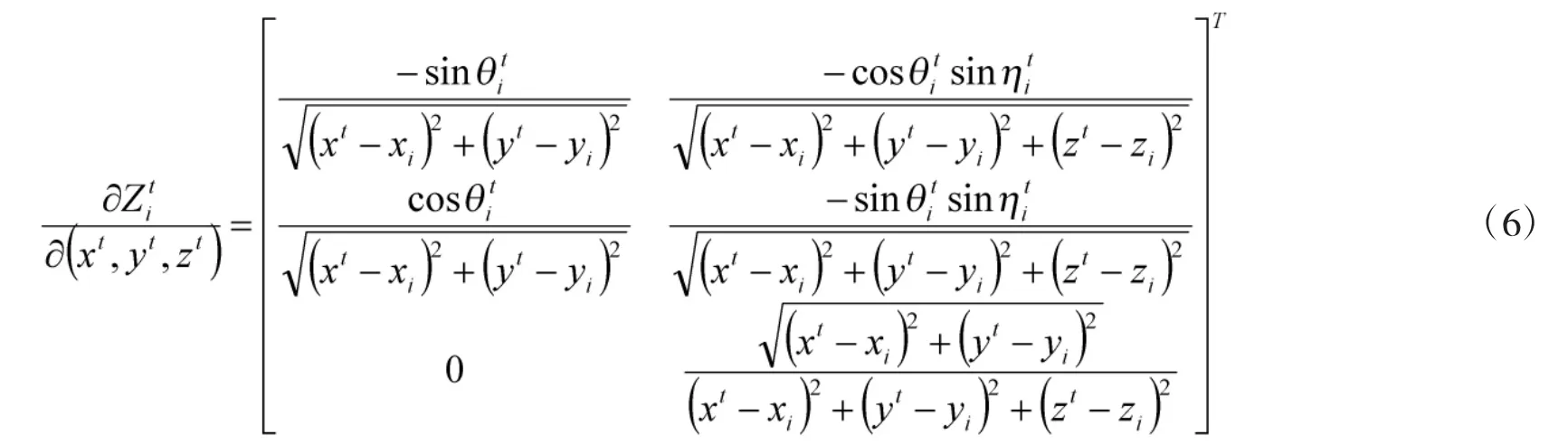
3 基于CRLB 的行列式最大最小化的传感器动态选择

3.1 传感器选择优化模型

3.2 基于半定规划的传感器选择

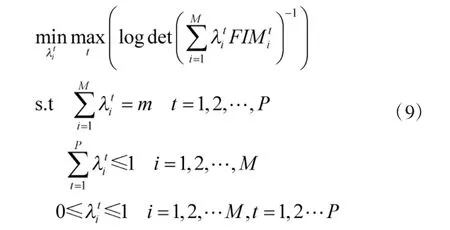
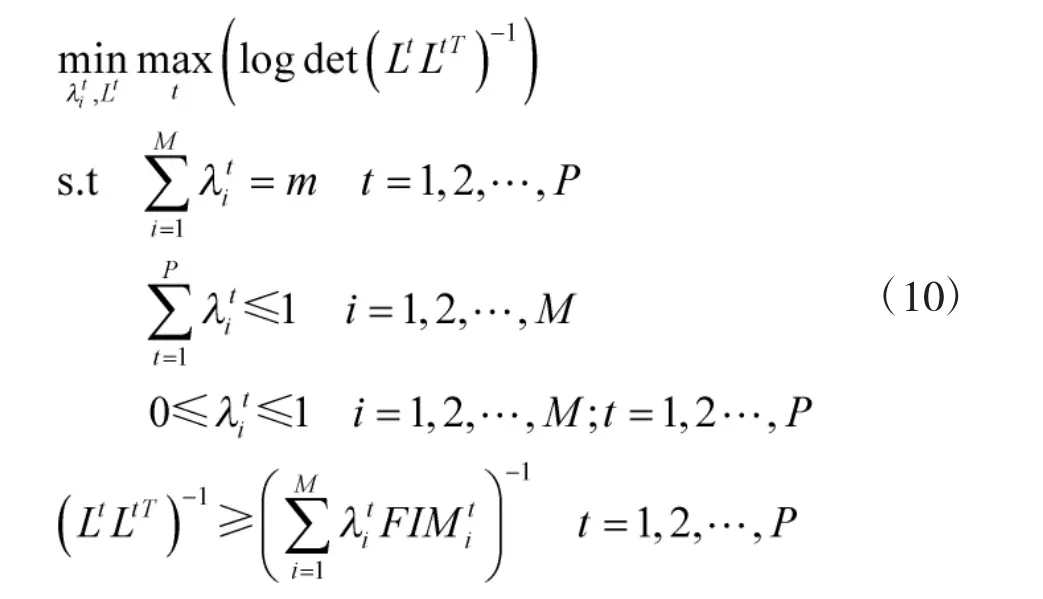
根据舒尔补不等式［8］

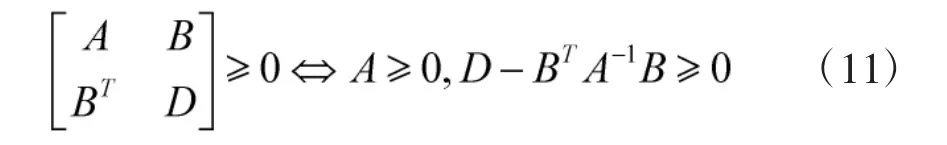
可以得到：

根据下三角矩阵的性质对目标函数进行变换得到：

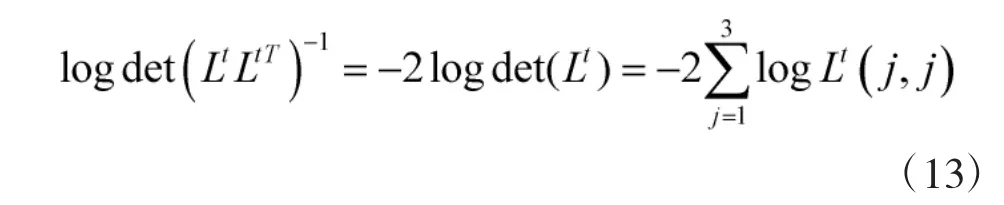
此时优化问题转化成如下半定规划（SDP）问题：

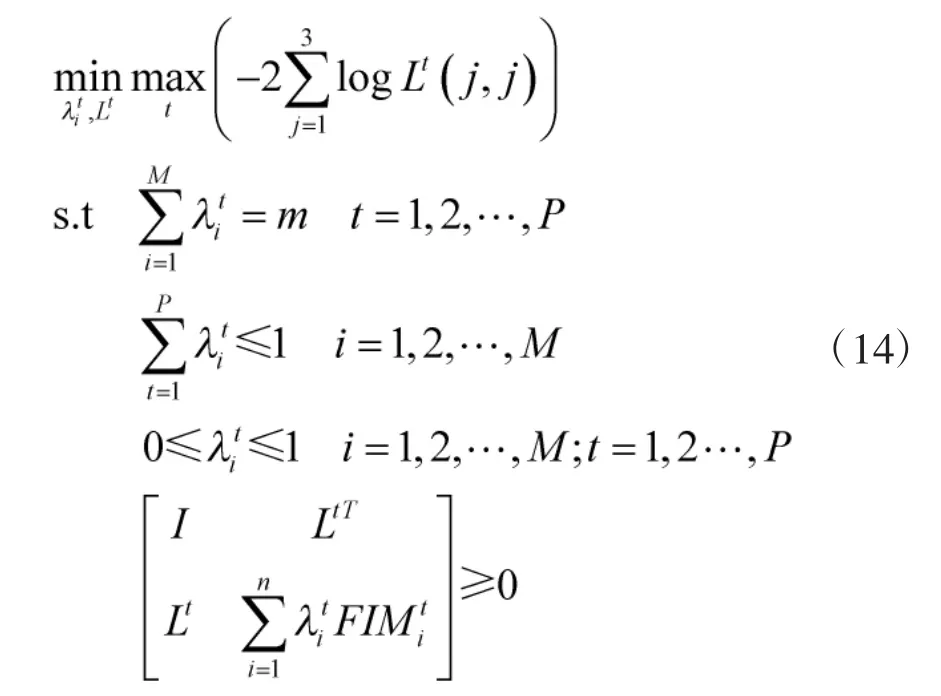
用以上方法得到最佳的传感器后再基于所选择的传感器采用IMM［9］跟踪算法对多个机动目标进行跟踪。

4 仿真及分析

图2 传感器位置分布图

采用CV、CA、CT 3 种模型作为参考模型来跟踪机动目标，目标1 和目标2 模型的先验概率和Markov 转移概率均设为相同，即

图3 不同算法下最佳传感器选择结果

将SDP 算法和基于松弛算法和随机分配进行仿真比较分析，图3 给出基于松弛算法的传感器分配结果和基于SDP 算法的传感器分配结果，不同的算法获得的最佳传感器集合不同。

为了进一步分析传感器-目标几何关系对传感器选择的影响，采用定位精度的几何稀释（GDOP，Geometrical Dilution of Precision）指标来描述定位误差的三维几何分布，其表达形式如下：

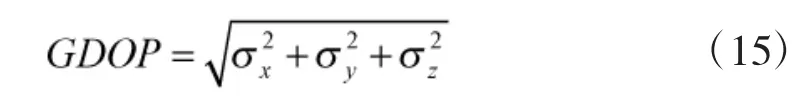
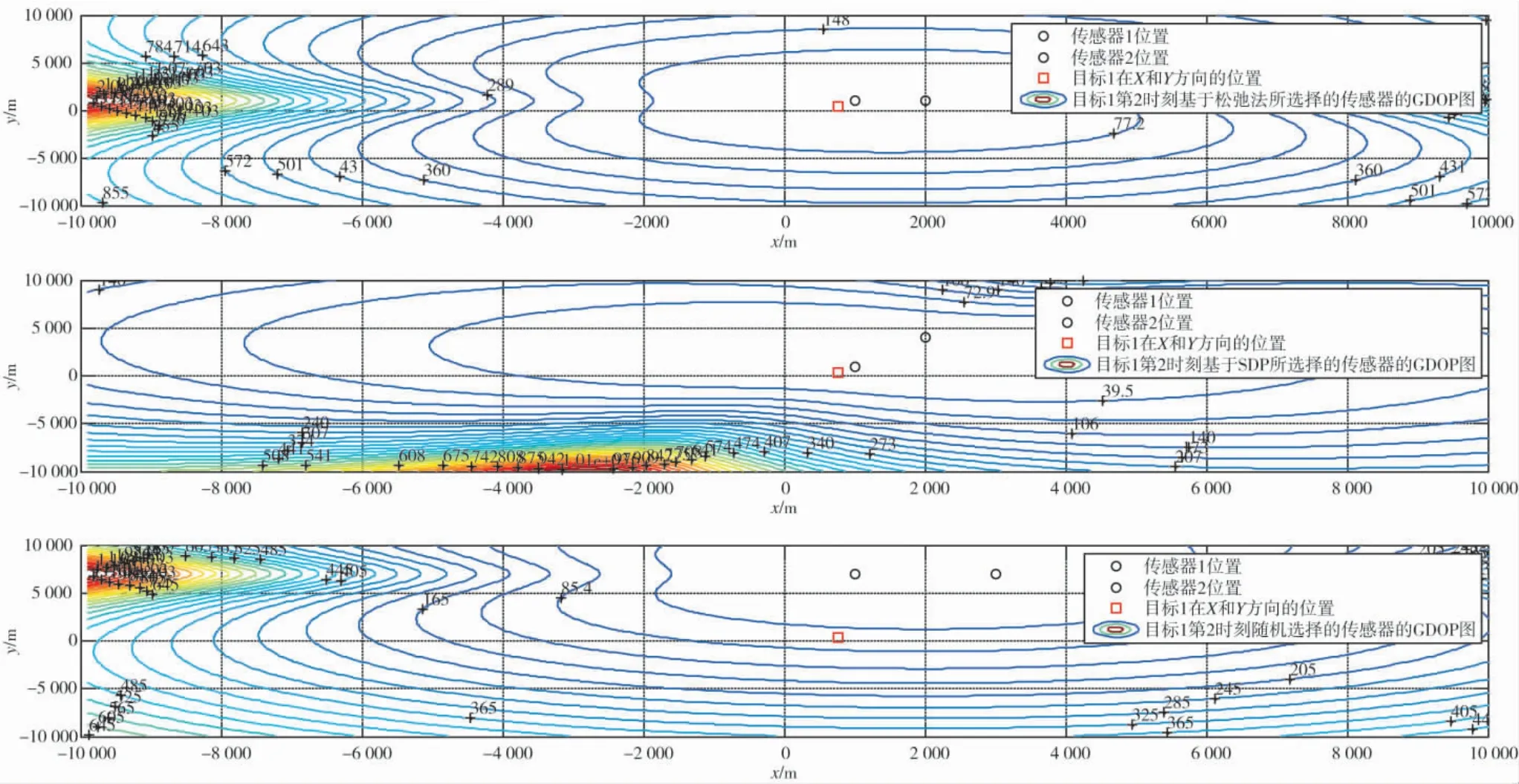
图4 目标1 传感器选择和GDOP 等值线图

图5 目标2 传感器选择和GDOP 等值线图

图4 和图5 分别给出某一时刻目标1 和目标2对应的GDOP 等值线图，图4 和图5 显示当目标在传感器阵列平面上的投影点与可探测被动传感器位置在一定程度上靠近时，GDOP 定位误差减小，几何关系明显改善。然而受高度影响，无法得到最佳传感器位置与目标实际高度之间的最优几何关系。

图6 目标位置RMSE

图6 给出了各目标位置均方根误差曲线，对于目标1，基于SDP 的传感器选择算法和基于松弛的传感器选择算法的跟踪性能，明显优于随机传感器选择算法；对于目标2，基于SDP 的传感器选择算法跟踪性能，明显优于基于松弛的传感器选择算法和随机传感器选择算法。

5 结论

本文针对三维空间下机动目标，提出了一种基于半定规划的无源协同跟踪下最佳传感器选择方法。首先，推导了三维空间下目标的CRLB，分析了CRLB 指标与传感器和目标之间关系。以此，构建基于CRLB 的行列式最大最小化指标的传感器选择模型。采用SDP 方法将上述组合优化问题转化成凸优化问题，并进行优化求解。仿真结果显示以CRLB 的行列式作为指标，通过改善传感器和目标之间的几何关系可以提高跟踪性能。与松弛算法和随机选择算法两种算法进行比较研究，基于SDP 的传感器选择可以进一步提高无源协同跟踪的精度。