改进的GM(1，1)幂模型的构建与应用

马永梅　王淑超

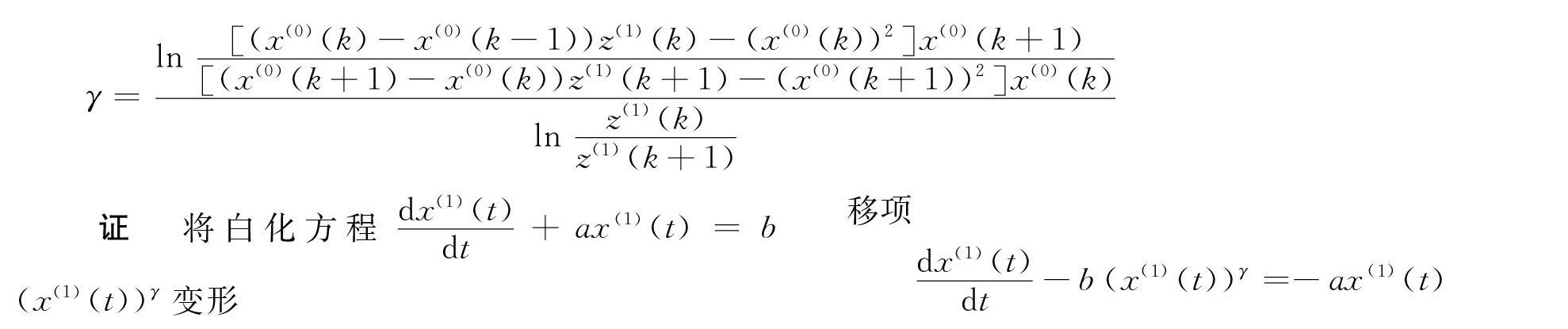
摘 要 在构建GM（1，1）幂模型中，经常利用一阶非齐次线性方程的常数变易法求得GM（1，1）幂模型白化方程的解，再利用白化方程，在灰色系统信息覆盖原理下经过离散化处理推导出参数γ的计算公式，并利用最小二乘法求解参数a，b.但是在求解过程中由于离散化的处理，造成了时间响应预测函数精度的下降。为了弥补精度下降的缺陷，对于预测模型利用PSO算法进行了系数修正.案例对比研究发现，传统的GM（1，1）预测效果最差，改进的GM（1，1）幂模型预测效果最好.

关键词 预测;GM（1，1）幂模型;白化方程; PSO算法;参数优化

中图分类号 N941.5 文献标识码 A

Abstract In the construction of GM（1，1） power model， the solution of whitening equation of GM（1，1） power model is often obtained by constant variation method of firstorder nonhomogeneous linear equation. Then， by using whitening equation， the calculation formula of parameters is deduced by discretization under the principle of information coverage of grey system， and the parameters are solved by least square method. In order to compensate for the defect of decreasing precision， the PSO algorithm is used to modify the coefficients of the prediction model. A case study shows that the traditional GM （1，1） model has the worst prediction effect and the improved GM （1，1） power model has the best prediction effect.

Key words Prediction; GM（1，1） power model; Whitening equation; PSO algorithm; Parameter optimization

1 引 言

GM（1，1）幂模型是一类非线性灰色模型，其背景值与灰导数成分能够满足平射关系。随着γ取值的不同，该模型适用于不同的原始序列模型.GM（1，1）幂模型的应用非常广泛，特别是在“小样本、贫信息”的不确定系统或者缺乏数据的情况下，获得了较为成功的应用，在预测和决策领域中占有一定的重要地位.

之前的研究多集中在GM（1，1）幂模型的应用上，例如曾亮和骆世广（2015）[1]针对传统灰色GM（1，1）预测模型维数确定困难、适用范围小和预测精度不高等局限性，提出了一种能处理复杂序列的动态

的最佳维数GM（1，1）幂模型，以我国居民收入的基尼系数为研究样本做了预测分析;郭晓君等（2015）[2]针对因发展变化受众多因素影响而具有饱和增长趋势或单峰特性的原始波动序列，为了提高预测精度，以灰色GM（1，1）幂模型为基础，构建了自忆性原理与优化GM（1，1）幂模型的耦合预测模型，最后以我国高中升学率的数据为例验证了所构建模型的优越性和有效性。黄跃华和陈海山（2016）[3]通过优化幂指数研究了在港口吞吐量的预测问题，郭毅和高建民（2016）[4]根据冻胀区高速铁路轨面不平顺的发展特征，应用灰色系统理论，建立以冻胀区高速铁路轨面不平顺检测，张思俊和陈淑燕（2016）[5]针对灰色GM（1，1）幂模型存在的缺陷，从背景值和初始条件两个方面对GM（1，1）幂模型进行参数优化。但是前期研究成果对于模型构建的详细步骤研究不够，虽然王正新等（2009）[9]对幂模型的求解有介绍，但是过程并不完整，因此系统完善地给出GM（1，1）幂模型的构建方法是有必要的.

由表2看到，传统的GM（1，1）模型预测结果的平均相对误差2.51%，而GM（1，1）幂模型的预测结果更加接近原始数据，预测的平均相对误差为0.29%，预测的准确性已经不错.但是考虑到离散化处理造成的精度损失，引进对时间响应函数引入修正系数的结果更为精确，由表2看到PSO改进的幂模型平均相对误差为0.26%，预测精度最高.因此改进后的GM（1，1）幂模型可以更好地预测未来几年石油的消费量，代入公式预测2018、2019年的消费量为（0）（9）=4664.77（百万吨），（0）（10）=4727.3（百万吨）.可见，未来两年的石油消费量仍呈现递增的趋势.

6 结 论

20世纪80年代初，邓聚龙提出了灰色系统理论.灰色理论研究对象以“贫信息”、“少数据”为主要特点，目前GM（1，1）模型已经有较为成熟的研究成果，但是纵观灰色理论研究成果，对于GM（1，1）幂模型的研究相对较少，尤其对于幂模型的参数求解问题研究较少.利用等式转换、信息覆盖原理等方法在前期研究的基础上给出了GM（1，1）幂模型的建模过程，推导出了模型参数的计算公式，计算过程相对于之前的研究结果更为简洁和系統，给模型参数的求解做了一定的完善和补充.最后结合全球近几年石油的消费进行了模型精度预测对比分析，研究发现，传统的GM（1，1）模型的预测精度比较低，一般预测值高于真实值. GM（1，1）幂模型的预测精度比较好，但是在离散化处理时会导致精度的损失，因此预测的效果也并不是最为理想.为了提高GM（1，1）幂模型的预测精度，通过PSO优化算法对白化方程的解进行优化处理的预测结果最为准确.另外，在白化方程求解中，取（1）（0）=x（0）（1），造成了对初值的依赖，如何避免仍需要进一步深入研究.

参考文献

[1] 曾亮，骆世广.动态的最佳维数GM（1，1）幂模型在基尼系数预测中的应用[J].数学的实践与认识，2015，45（1）：88-95.

[2] 郭晓君，刘思峰，方志耕，吴利丰.融合自忆性原理的优化GM（1，1）幂模型构建及应用[J].系统工程与电子技术，2015，37（1）：117-122.

[3] 黄跃华，陈海山.优化的GM（1，1）幂模型在港口吞吐量预测中的应用[J].中国航海，2016，39（2）：131-134.

[4] 郭毅，高建敏.基于GM（1，1）幂模型的冻胀区高速铁路轨面不平顺发展预测[J].铁道科学与工程学报，2016，13（5）：791-799.

[5] 张思俊，陈淑燕.GM（1，1）幂模型的优化方法及其应用[J].系统工程，2016，34（8）：154-158.

[6] 王正新，党耀国，刘思峰，练郑伟.GM（1，1）幂模型求解方法及其解的性质[J].系统工程与电子技术，2009，31（10）：2380-2383.

[7] 刘思峰.灰色系统理论及其应用[M].北京：科学出版社（第三版），2004：149-169.

[8] 刘帅.基于粒子群优化的GM（1，1）幂模型电力负荷预测研究[D].北京：华北电力大学经济与管理学院，2014.

[9] 崔传智，吴忠维，李昱东，黄广庆，李荣涛，金超林.应用PSO-改进GM（1，1）模型预测油田产量[J].数学的实践与认识，2018，48（17）：119-123.