基于齿向修形的航空渐开线花键副抗微动磨损研究

薛向珍 霍启新 郑甲红 陈 曦 秦利云

1.陕西科技大学机电工程学院，西安，7100212.西安航天发动机厂35车间，西安，710061

0 引言

渐开线花键具有良好的导向性、定心性及大的扭矩传输能力，被广泛应用于航空减速器、航天发动机涡轮泵等动力传输系统中。航空花键副在飞机起飞、巡航、着陆过程中承受变扭矩、轴向力以及弯矩形式的周期波动载荷，微动磨损失效非常严重，严重影响航空花键副使用过程中的稳定性和安全性，故为了延长花键副使用寿命、提高其使用可靠性，必须采取相应措施以减缓其微动磨损。

近年来，有关航空渐开线花键副微动磨损的研究越来越多[1-4]。LEEN等[5]在实验验证的受扭矩和轴向力载荷的花键有限元模型基础上，考虑轴向齿廓修形及摩擦因数的影响，对花键的三维摩擦接触进行了研究。RATSIMBA等[6]、DING等[7]通过实验测得材料摩擦因数及磨损系数后，利用三维有限元模型得出航空渐开线花键副的接触应力和滑移距离，采用修正的Archard 方程计算了磨损深度。 DING等[8-9]利用有限元方法模拟加载扭矩、轴向力的主循环载荷，并结合弯矩和扭矩波动的次循环载荷，对航空花键副的磨损疲劳行为进行了研究。MADGE等[10]预测了磨损对磨损疲劳分析的作用。胡正根等[11-12]针对航空渐开线花键副的微动损伤展开了相关研究。此类研究只是简要、零星地概述了引起微动磨损的原因及其控制减缓措施，具体针对航空渐开线花键副微动磨损进行减磨的研究相对较少。

在综合考虑了航空渐开线花键副微动磨损失效的主要原因后，本文采用Abacus有限元法对某航空渐开线花键副的接触应力及相对滑移距离的分布规律进行分析，基于以往对航空渐开线花键副微动磨损量的预估方法，提出一种新的航空渐开线花键副修形方法，并将其与传统修形方法进行对比，通过合理修形，提高航空花键副抗微动磨损能力。

1 渐开线花键齿向载荷分布规律

对航空渐开线花键副而言，载荷分布、分配是研究其微动磨损行为的基础，同时也是微动磨损领域的热点和难点问题之一[13-15]。CHASE等[16-17]考虑齿侧间隙，研究了花键副实际啮合齿数和载荷分配。工程实践中，花键副承受转矩时，各截面不同的扭转角度导致转矩沿轴线分布极为不均。

图1中，R2为花键轴半径；r1为内花键齿根圆半径；R1为内花键轮毂外径；Le为有效接触长度，mm。系统输入转矩T1对任意点x有

Tex(x)+Tin(x)=T1

(1)

式中，Tin(x)为传递到花键孔上的转矩，N·m；Tex(x)为传递到花键轴上的转矩，N·m。

T1由花键孔再经花键传递到花键轴时，转矩沿轴向的分布方程为

t(x)=dTex(x)/dx=Kθ(θin(x)-θex(x))

(2)

式中，t(x)为花键轴上任意点x处的转矩集度；Kθ为单位长度花键副的扭转刚度，N/rad；θin(x)、θex(x)分别为轴向距离x处花键孔和花键轴的转动角，rad。

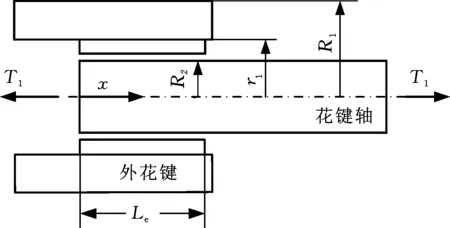
图1 花键副啮合几何示意图Fig.1 Geometric diagram of spline coupling

设载荷分布函数F(x)为转矩分布集度函数t(x)与单位长度平均转矩之比[15]，即

F(x)=t(x)/(T1/Le)

(3)

轴向距离x处花键孔和花键轴的转动角θin(x)和θex(x)计算公式为

(4)

(5)

(6)

(7)

式中，G为材料的剪切模量，GPa；Min为内花键剖面抗扭模量，GPa；Mex为外花键剖面抗扭模量，GPa。

对式(2)微分，则有

(8)

又由于Tex(x)+Tin(x)=T1，则有

(9)

利用边界条件Tex(0)=0，Tex(Le)=T1得渐开线花键的轴向载荷分布函数：

(10)

当花键副材料剪切模量G=85 GPa、弹性模量E=202 GPa、泊松比μ=0.25、系统输入转矩T1=35 013 N·m，单位长度花键副的扭转刚度Kθ为160～350 MN/rad[15]时，所研究花键副的基本参数如表1所示。该花键副在不同材料剪切模量、扭转刚度、接触长度、抗扭模量时，沿轴向的载荷分布如图2所示。

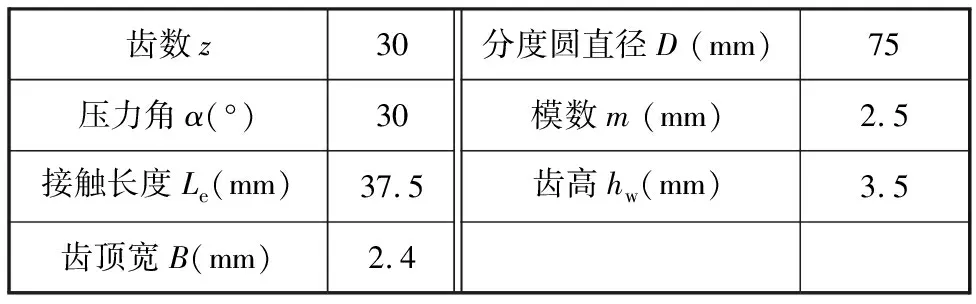
表1 渐开线花键副几何参数

由图2可以看出，花键副的扭转刚度、剪切模量、抗扭模量、结合长度不同时，花键副沿轴向的载荷均是越来越大的。随着剪切模量增大，花键副轴末端的载荷也增大，当剪切模量达到最大时，末端轴向载荷分布系数最大，达到0.157， 同一曲线上(即剪切模量最大对应的曲线)轴始端的载荷减小，轴上由始到末的载荷变化幅度增大；花键副扭转刚度增大，花键副轴末端的载荷最大值增大，轴始端的载荷减小，轴上由始到末的载荷变化幅度增大，载荷系数的变化幅度达到0.044；内外花键剖面抗扭模量增大时，花键副轴始末两端的载荷均增大；花键副的结合长度增大时，花键副轴始末两端的载荷都减小。由此可得出，扭转刚度、材料剪切模量、剖面抗扭模量、结合长度对渐开线花键副的轴向载荷分布都有一定影响。造成这种结果的直接原因是花键副材料的选取、花键副的定心径向间隙、侧向间隙以及花键节距误差等。如果在设计中选取了不恰当的几何参数，或在加工、装配过程中出现过大的误差，那么这些不恰当的几何参数和误差会使花键副实际齿廓形状与理想齿廓形状在轴向上存在差异，进而在啮合时造成载荷沿花键副轴向的分布不均。同时，设计中的参数选取不当会使花键副出现歪斜、不同心，内外花键的空间位置误差和径向力的作用使花键轴与花键套的轴心发生偏移，使键齿齿型沿轴向产生不同程度的变形，从而引起各截面的扭转角度不同，导致载荷沿轴线分布不均。这将造成花键副局部接触应力很大，严重影响花键副的寿命和可靠性。对于航空渐开线花键副，可以通过减小其齿侧间隙，使其实际参与啮合的齿对数增加，进而改变其接触区域，提高啮合的平稳性，减小动载系数和齿面最大接触应力。

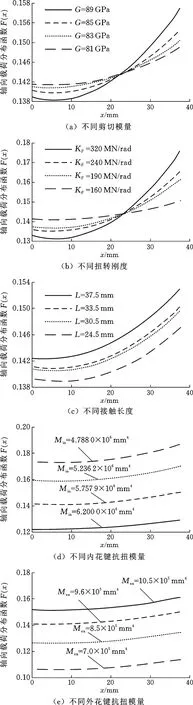
图2 花键副沿轴向的载荷分布Fig.2 Axial load distribution of spline coupling

2 渐开线花键副齿向修形设计

2.1 花键副轴向载荷均分条件

为了减小花键副接触应力的最大值，使轴向载荷分布均匀，达到减小花键副抗微动磨损的作用，需要设计出合理的花键副的结构。由式(10)可得x=Le时，花键副载荷分布函数最大值

(11)

由式(11)可知，载荷分布函数F(x)的最大值Fmax与花键副扭转刚度、材料剪切模量、剖面抗扭模量、结合长度有关。减小花键孔的抗扭刚度G1Min可以减小Fmax，故为了使转矩沿轴线分布均匀，应当使花键孔的刚度沿花键副长度逐渐减小。

由式(10)可以看出，转矩沿轴向分布均匀须满足下述条件：

(12)

即

(13)

实现载荷沿轴向均匀分布的第一种方法是通过花键孔外径变化达到改变M1的目的。

式(13)表示的花键孔外径虽然可以使转矩沿轴向分布均匀，但在实际中无法实现，因为在x=Le处，r1=R1即花键孔厚度为0；在x=0处，花键孔厚度则为无穷大。实际工作中采用下式确定花键孔外径[18]：

(14)

实现载荷沿轴向均匀分布的第二种方法是沿轴线改变齿厚，即采用鼓形修形。由于第一种方法基本无法实现，综合各方面因素，本文采用鼓形修形的方法实现转矩沿轴线分布均匀。

2.2 传统修形方法介绍

渐开线花键齿的修形主要是指沿齿向对齿面进行微量修整，使其偏离理论齿面。通过齿向修形可以改善载荷沿轮齿接触线的不均匀分布情况，提高齿轮承载能力。近几年，学者对齿轮修形做了大量的研究，所采用的齿向修形方法也较多，常用且修形效果较好的方法有齿端修薄、螺旋角修形、鼓形修形[19]。本文研究的是渐开线直齿花键齿，通过分析比较，最终采用鼓形修形方法对花键齿进行修形。图3中，Δ1和Δ2均为修形量。鼓形修形函数的建立需要确定两大因素：鼓形量大小；鼓形中心在齿向方向上的位置。鼓形量的确定需考虑众多因素，目前主要有两种确定方法：①参考经验公式；②采用数值方法计算。

图3 鼓形修形Fig.3 Crown modification

鼓形修形量常见的经验公式有以下几种[20]：

δ1=βx/2

(15)

δ2=0.7Fm/B

(16)

δ3=B/4 000+fg/2

(17)

fg=A(B/10+10)

(18)

式中，βx为齿向脱开量，mm；A是与精度有关的系数，具体数值见参考文献[21]；Fm为圆周力，N；fg为齿向误差，mm。

鼓形修形的另一个重要参数是鼓形中心的位置，一般资料推荐选在齿宽的中点，但这样选取的修形结果不是最好，文献[22]认为中心距

Bm=2Bwe

(19)

式中，Bwe为有效接触齿宽，mm。

若计算出的Bm>B，则取Bm=B。

2.3 数值法确定最佳鼓形修形曲线

数值法即通过一种数值计算来确定合理的鼓形量及修形中心。 键齿实际长度为L，mm。设修形曲线表达式为e(x)=ax2+bx+c，则可得到以下关系式：

(20)

从而得修形曲线的对称轴公式：

(21)

由于研究对象是花键齿修形，为了保证齿上至少有一点不被修形，抛物线顶点必须在齿顶两侧任一侧的轴线上，故抛物线对称轴须满足：

(22)

即可得对称轴及曲线方程中a、b、c的值:

(23)

(24)

故引入修形函数后，式(8)可化为

(25)

若键齿沿轴向的载荷均匀，即输出扭矩延轴向为常数，则式(25)应该为零[18]。结合式(20)可得：

(26)

最佳鼓形修形量为

(27)

(28)

则最佳修形曲线方程为

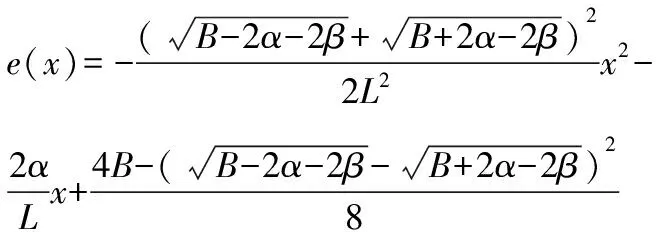
(29)

3 航空渐开线花键副微动磨损预估分析

3.1 航空渐开线花键副接触特性分析

所研究的航空渐开线花键副的材料为18CrNi4A钢(渗碳层厚度为0.6～0.7 mm，表面硬度为HRC56.3)，各齿间的齿侧间隙如表2所示。在CATIA中对表1所示参数的某航空渐开线花键副进行实体建模并导入Abaqus：定义单元类型为C3D8R；材料弹性模量为210 GPa，泊松比为0.28，密度为7 800 kg/m3，摩擦因数为0.28。建立有限元模型，如图4所示。假定30对齿均参与啮合，将内花键设置为目标面，将花键轴设置为接触面，建立接触对。根据花键副运动规律，将内花键外圆柱面绕轴转动之外的5个自由度进行约束，外花键内圆柱面绕轴转动之外的5个自由度也进行约束。

表2 齿侧间隙分布

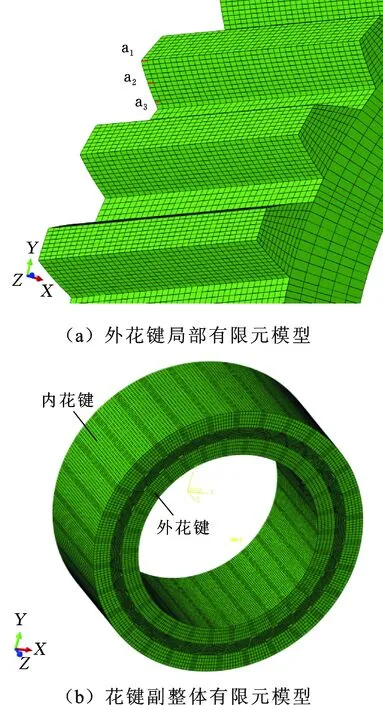
图4 渐开线花键副有限元模型Fig.4 The finite element model of involute spline coupling

航空花键副所受载荷形式为一个主循环扭矩伴随多个次循环扭矩。施加载荷时，为了更接近实际工况，仿真时将航空渐开线花键副的实际载荷简化为均值形式的主循环载荷，和呈谐波形式围绕均值上下波动的次循环载荷的叠加形式。当系统输入扭矩为T1时，花键副所受力矩表达式为

Tg(t)=KvTm(1+εTcosωTt)

(30)

式中，Tm为外激励转矩的均值，N·m；εT为外激励转矩的幅值波动系数，取0.1；Kv为动载系数，取1.123 8；ωT为系统的角速度，rad/s。

根据ωT=πn/30可得，循环周期τ=60/n，其中，n为系统的转速，r/min。

然后将一个循环周期(0～2π)内的转矩Tg(t)离散为5个载荷步(i=1，2，…，5)，即ωTt=0，π/2，π，3π/2，2π分别对应一个转矩。对内花键一端面施加反向扭矩载荷，模拟一端输入的渐开线花键副工作状况，当系统输入平均转矩Tm=35 013 N·m，转速n=300 r/min时，一个循环内每个载荷步对应的转矩及每个载荷步结束的时间如表3所示。对于图4所示花键副有限元模型，选择第1～5载荷步进行动态仿真分析，得到花键副初始模型的接触应力及滑移距离，如图5所示(篇幅所限只给出第2个载荷步的结果。

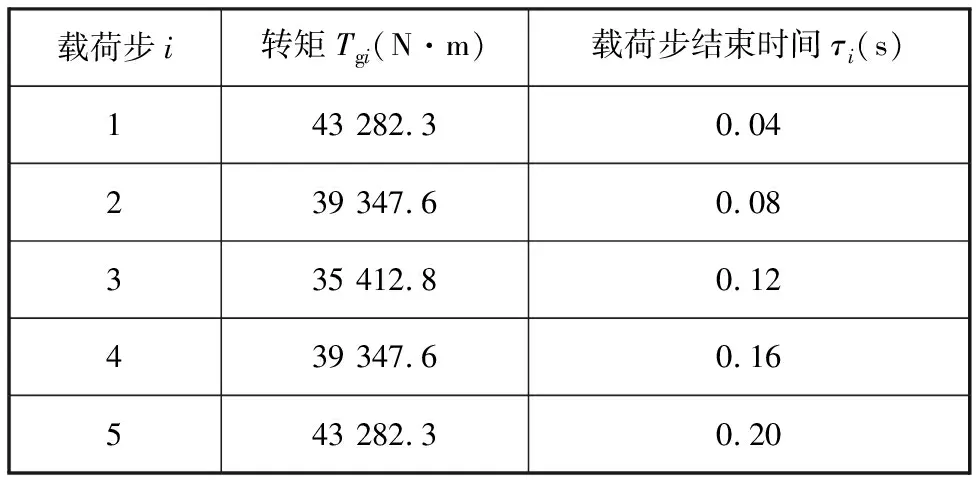
表3 加载情况

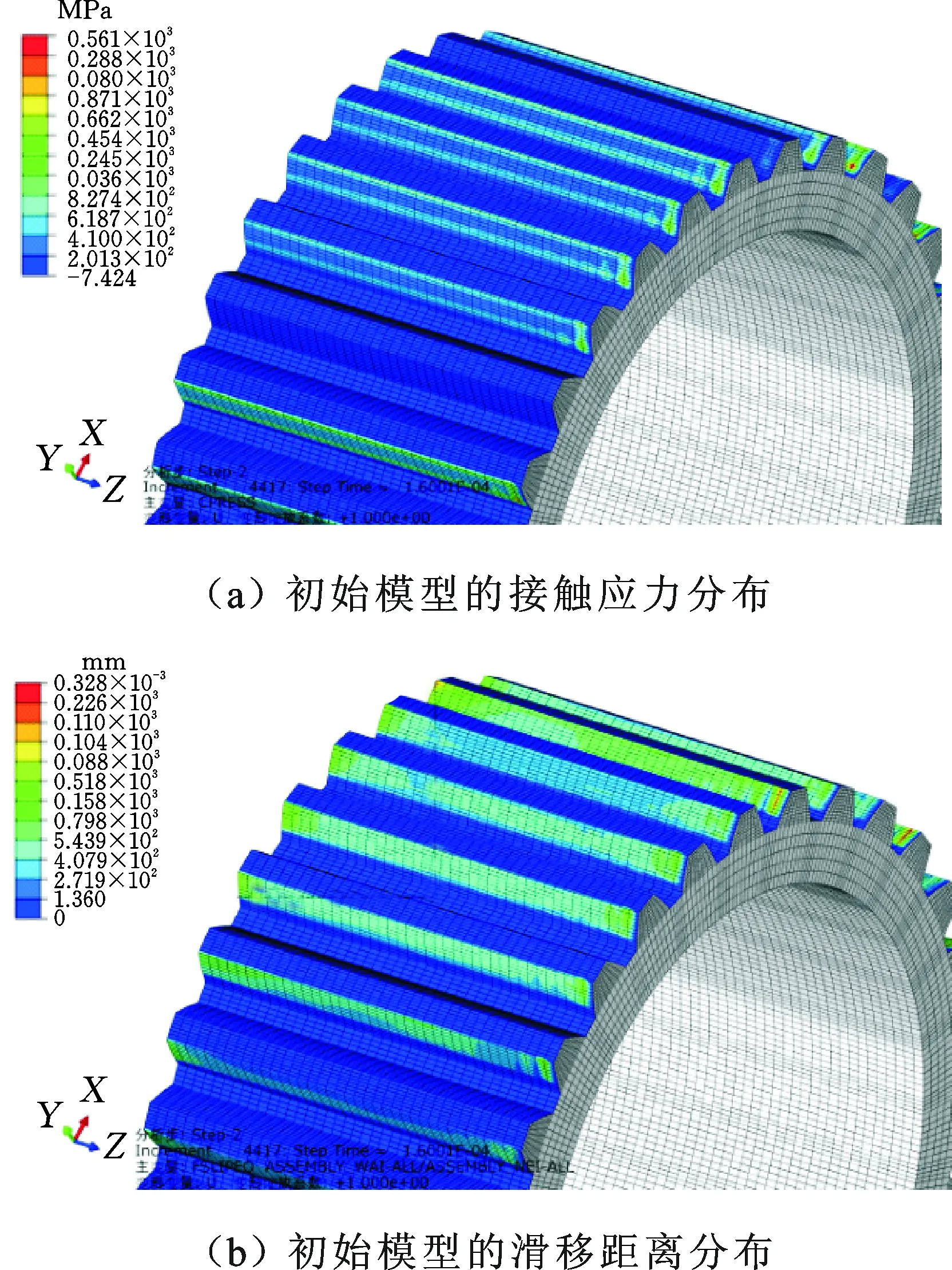
图5 有限元仿真云图Fig.5 The map of finite element simulation

由图5可以看出，每个齿上的接触应力和滑移距离均不同。接触应力和滑移距离均沿着轴向，从转矩输出端到转矩输入端是越来越大的。由图5还可以看出，部分齿并未参与啮合，齿上并没有接触应力和滑移距离。第2个载荷步时，实际参与啮合的齿中，接触应力最大为561 MPa，最大滑移距离为0.328 μm，均位于第2对齿的齿顶，第25对齿的接触应力和滑移距离次之，这与齿侧间隙大小有关，后续会进行相关研究。

3.2 航空渐开线花键副微动磨损预估分析

3.1节对某航空渐开线花键副初始模型进行接触分析，得出给定工况下该航空渐开线花键副各齿任一点在每个载荷步时的接触应力及滑移距离，将其分别代入Archard 模型即可得出其任一点在一个载荷循环下的微动磨损量[9]：

(31)

式中，s为相对滑移距离，mm；p为接触应力，MPa；k为磨损系数，MPa-1。

需要注意的是，进行渐开线花键副微动磨损量计算时，为了使计算结果更为准确，每一个载荷步均需将一个载荷循环作用下的各齿任一点的磨损量作为新的初始条件，在Abaqus中对初始花键齿廓表面的节点坐标进行修改。由于航空渐开线花键副键齿齿廓为渐开线，且受工艺、制造加工、设计等影响，其键齿面摩擦副沿齿廓方向的接触非常不均匀，故修形时，模型接触区域表面的每个节点坐标沿齿廓方向和轴向均不同。设(xi,yi,zi)、(xm,ym,zm)为外花键齿廓上任意两点i、m未修改前的坐标，(xi,yi-Δθi,zi)、(xm,ym-Δθm,zm)为点i、m修改后的坐标，Δθ为任意两点i、m修形前后的夹角，R为任意两点i、m处的半径，各节点坐标均以柱坐标表示，渐开线花键副的节点坐标修改原理如图6所示。

图6 键齿修形几何示意图Fig.6 Geometric diagram of spline tooth modification

齿面节点修改过程中，如果该节点的磨损量大于表面单元法向尺寸，就会对仿真结果的准确性产生较大影响，甚至导致仿真失效。在网格划分时，如果采用的单元法向尺寸大于整个磨损过程中的累积磨损量，会使得分析过程中网格质量较差，计算精度较低，故为了确保仿真过程中节点位置不发生畸变，又能获得较好的模拟精度，这里采用Abaqus内置的ALE自适应网格光滑算法对已修改的齿磨损表面节点进行重置[23]，即根据图6所示原理在Abaqus中修改齿磨损表面节点后，再经Abaqus自带的ALE自适应网格光滑算法对网格质量进行优化调整，调整原理如图7所示。其中，节点H周围分布着4个单元，通过调整节点H的位置至H′处，从而优化修改节点坐标后的网格质量。

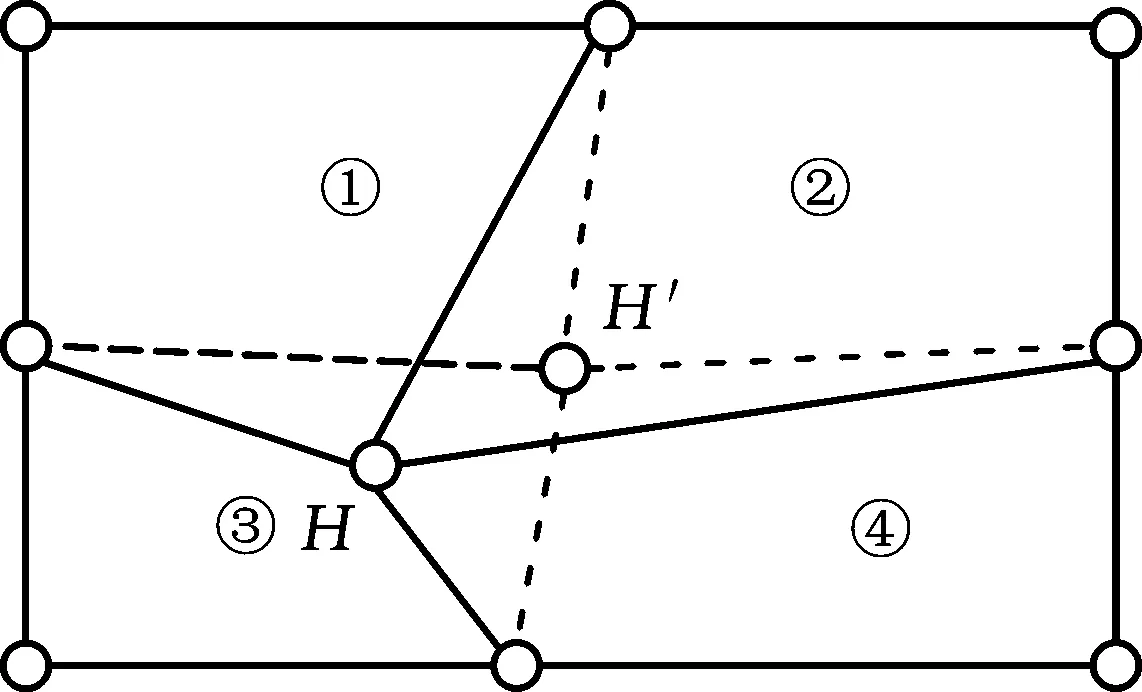
图7 节点重置原理图Fig.7 Schematic diagram of node reset

然后继续计算节点重置后下一个载荷循环所对应的各齿任一点的接触应力、滑移距离以及微动磨损量，依次循环计算。该过程采用FORTAN实现。当这一载荷循环的接触应力、滑移距离以及微动磨损量计算完毕之后，Abaqus会继续自动启动其自带的ALE自适应网格方法对修改完的节点坐标进行节点重置，继续计算下一个小循环内的微动磨损量，如此循环迭代。若一个小循环内的微动磨损量太小，则容易影响键齿修形精度，且修形次数若是以一个小循环为单位，会大大增加计算量，故为了减少计算量，将ΔN作为一个磨损循环增量，即以固定的多个小循环次数ΔN为一个磨损量计算的循环单位，则渐开线花键副微动磨损量预估流程如图8所示。

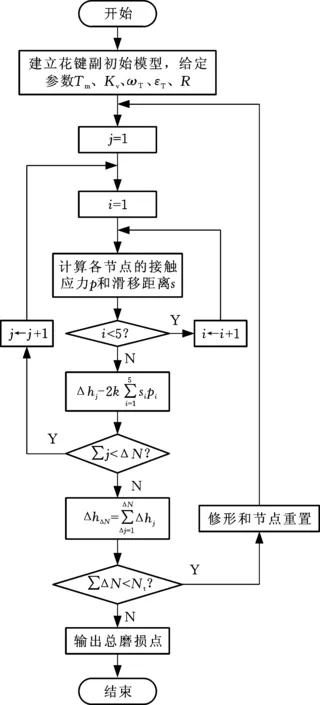
图8 微动磨损预估流程Fig.8 The estimated process of fretting wear

3.2.1未修形花键副的微动磨损预估分析

根据图8所示的流程预估某航空渐开线花键副的微动磨损量,如图9所示，其中，ΔN=106。由图9可以看出，花键副微动磨损量随着载荷循环次数的增大而增大。轴端(x=0)处，花键齿接触区域顶端的微动磨损比根部的微动磨损严重，而接触中间区域的磨损最轻。此时，接触区域的最大磨损量为78 μm；轴中间位置(x=18.75 mm)处，接触区域齿根附近的微动磨损比接触区域顶端的严重，接触区域的中间位置的磨损最轻，接触区域的最大磨损量为112 μm；轴末端(x=37.5 mm)的磨损与轴中间位置的磨损相似，最大磨损量为85 μm。

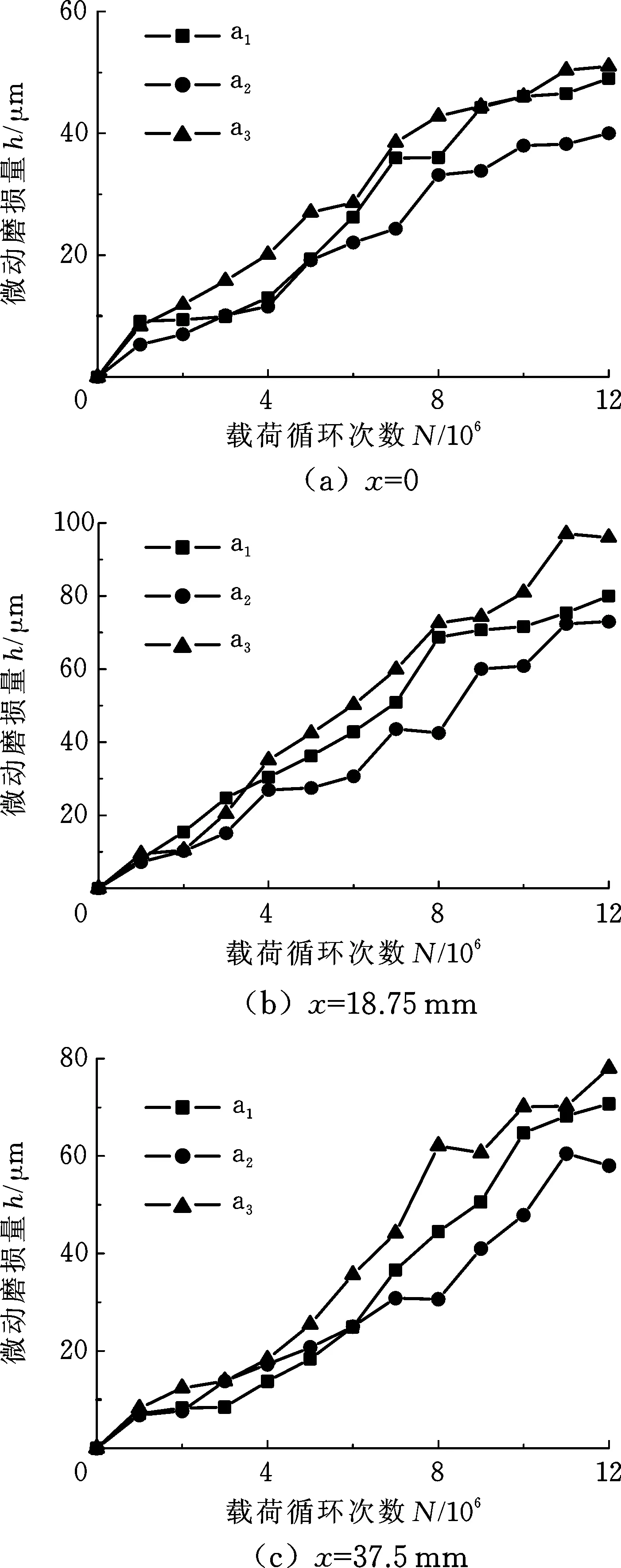
图9 修形前的磨损量随循环次数的分布Fig.9 Distribution of fretting wear with load cycles before modification

从图9中还可以看出，无论接触面靠近齿顶、齿中，还是齿根处部位，其微动磨损量在x=0处最小，在x=37.5 mm处最大(末端为转矩输入端)。

3.2.2修形后的花键副的微动磨损预估分析

对某航空渐开线花键副齿廓采用数值法修形后，计算其微动磨损量，得到的不同轴向位置处花键副键齿接触区域的磨损量随着载荷循环次数的变化情况，如图10所示(图中，a1表示接触区域顶端，a2接触区域中间位置，a3表示接触区域根部)。

图10 修形后的磨损量随循环次数的分布Fig.10 Distribution of fretting wear with load cycles after modification

从图10中可以看出，修形后的花键副微动磨损量随着载荷循环次数的增大而增大。在轴向各位置处，花键齿接触区域沿着轴向和齿廓方向的分布趋势与修形前基本一致。但通过修形，每一处的磨损量都有所下降。轴端(x=0)处，花键齿接触区域的最大磨损量为51 μm；轴中间位置(x=18.75 mm)，接触区域的最大磨损量为96 μm；轴末端(x=37.5 mm)，接触区域的最大磨损量为78 μm。

3.3.3修形方法对渐开线花键副微动磨损量的影响

为了得到更好的键齿修形方法，针对表1所示的渐开线花键副的几何参数和工况，当鼓形中心分别在齿中心处、有效齿宽2倍处时，采用2.2节所述的3种方法计算航空花键副微动磨损量沿轴向的变化；同时也按照2.3节介绍的数值法计算航空花键副的微动磨损量沿轴向变化，如图11所示。

图11 修形后不同径向位置处的磨损量沿轴向的分布Fig.11 The axial distribution of the fretting wear with different radial positions after modification

由图11可以看出，当修形位置在齿宽中心时，磨损的改善情况不如修形位置在Bm=2Bwe处。根据文中提出的数值法计算出来的修形量和修形位置进行修形，得到的花键副磨损分布较均匀，且磨损量降低幅度比3种推荐方法修形后的结果理想，有利于减少齿的磨损。

4 结论

(1)根据数值计算结果可知，在不同的扭转刚度、材料的剪切模量、剖面抗扭模量、结合长度情况下，花键副载荷从输入端到输出端均越来越大，这与有限元仿真结果一致。且从有限元仿真结果可以看出，齿侧间隙大小对键齿接触特性是有影响的。

(2)修形前后的花键副微动磨损量随载荷循环次数的增大而增大。在轴向各位置处，修形后的花键齿接触区域沿着轴向和齿廓方向的分布趋势与修形前基本一致，其每一处的磨损量都有所下降：轴端(x=0)处，花键齿接触区域的最大磨损量为51 μm；轴中间位置(x=18.75 mm)处，接触区域的最大磨损量为96 μm；轴末端(x=37.5 mm)处，接触区域的最大磨损量为78 μm。

(3)对于3种修形量，当修形位置在齿宽中心时，磨损的改善情况不如修形位置在2倍有效宽度处。根据本文数值法计算出来的修形量和修形位置进行修形后，得到的花键副磨损分布较均匀，有利于减少齿的磨损。