基于GA的NDNN结构与参数优化及其在入侵检测的应用

谭敏生，彭 敏，杨帅创，丁 琳，吴 冕

（南华大学 计算机学院，衡阳421000）

随着网络技术的高速发展与广泛应用，其安全问题备受国家与社会的强烈关注。入侵检测作为安全防范的一种重要手段，通过收集和分析计算机系统和用户的事件信息，及时发现入侵行为，提醒管理人员采取相应措施，采取有效的防范攻击，减少相应损失。在数据挖掘和机器学习理论的不断发展下，研究人员将机器学习算法与入侵检测相结合，以获得更高的检测效率和准确率。

1 入侵检测技术的研究现状

目前，基于机器学习的入侵检测技术，主要有统计、聚类和分类[1]。

在基于统计的入侵检测中，文献[2]提出标准偏差归一化熵精度分类器组合方法，利用9 个突出的分类器进行检测，检测率提高了3%～10%。文献[3]提出基于非线性相关系数的入侵检测方法，能够准确地提取网络流量记录之间的线性和非线性相关性，能够降低误报率，有效区分正常和异常行为。

在基于聚类的入侵检测中，文献[4]提出基于K均值聚类算法，提高了入侵检测的准确率；文献[5]采用所改进的K 均值方法建立新的小训练数据集，代表整个原始训练数据集，大大缩短了分类器的训练时间，提高了入侵检测系统的性能。文献[6]将K最近邻KNN（k-nearest neighbor）和支持向量机SVM（support vector machine）相结合来检测攻击。

在基于分类的入侵检测中，文献[7]将支持向量机分类算法应用于入侵检测；文献[8]提出了基于K均值聚类和序列最小优化分类相结合的混合机器学习入侵检测技术。文献[9]提出了基于机器学习的分类器来提高精确率。

然而，上述方法会随着数据维数的不断提高，丢失部分数据之间的隐形相关性，忽略一些有效的特征。近年来，深度学习已经成为当今研究的一个热点，深度神经网络等多种深度学习算法已经逐步应用于入侵检测中，取得了较好的效果。文献[10]提出了5 层神经网络结构的检测模型，将输出类别分成4 种情况并进行分析。文献[11]提出了基于多层人工神经网络和智能特征选择的入侵检测算法。文献[12]将人工神经网络作为分类器对网络中的数据包进行分类，同样取得了不错的检测效果；文献[13]利用遗传优化神经网络的入侵特征选取，进一步提高了网络入侵检测准确率。

然而，基于深度神经网络方法应用于入侵检测领域时，其检测性能易受权重、阈值、学习率的影响，导致准确率下降。在此，利用遗传算法强大的全局寻优能力，对文献[14]提出的基于NDNN 的入侵检测系统进行优化，通过遗传算法的选择、交叉和变异等操作，对深度神经网络的各隐藏层数目、学习率以及训练次数进行寻优。

2 深度神经网络分析

2006年Hinton[14]提出了深度神经网络DNN（deep neural network）算法。该算法具有更深的隐藏层数及神经元数，在处理大规模数据方面与浅层神经网络相比，能充分对数据特征进行非线性的映射，进一步挖掘各个特征之间的联系，提高特征提取的准确度。假定深度神经网络模型由1 个输入层、1 个输出层和2 个隐藏层所构成，如图1所示。

图1 深度神经网络结构Fig.1 Deep neural network structure

图中，输入层、输出层分别有n 和r 个神经元；隐藏层1 和隐藏层2 分别具有m 和a 个神经元；w1为输入层与隐藏层1 之间的权重；w2为隐藏层1 与隐藏2 之间的权重；w3为隐藏层2 与输出层之间的权重。

在前向传递中，假设：

x=［x1，x2，…，xn-1，xn］为输入层输入向量；

yb=［yb1，yb2，…，ybr］为输出层输入向量；

gb=［gb1，gb2，…，gbm］为隐藏层1 的输入向量，

go=［go1，go2，…，gom］为隐藏层1 的输出向量；

hb=［hb1，hb2，…，hbn］为隐藏层2 的输入向量，

ho=［ho1，ho2，…，hon］为隐藏层2 的输出向量。

w1is为输入层与隐藏层1 之间的权重，bs为隐藏层1 各个神经元的阈值，其中i=1，2，…，n；s=1，2，…，m。

w2su为隐藏层1 与隐藏层2 之间的权重，bu为隐藏层2 各个神经元阈值，其中s=1，2，…，m；u=1，2，…，a。

w3uj为隐藏层2 与输出层之间的权重，bj为输出层个神经元的阈值，其中u=1，2，…，a；j=1，2，…，r。

f（.）为激活函数，k 为样本中第k 个数据。

则有以下计算公式：

在反向传递中，因为输出层与真实值之间会存在一定的误差，所以通过误差函数来刻画预测值和真实值之间的误差。输入值往往是固定不变的，误差的调节需要通过对每个输出神经元对应的权重和阈值进行。

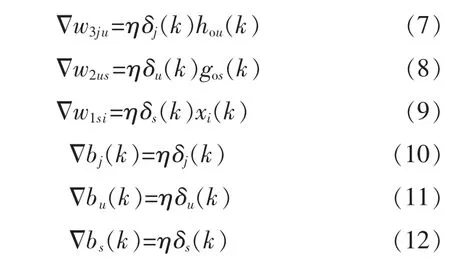
式中：δj（k）为误差函数对输出层各神经元求偏导的值；δu（k）为误差函数对隐藏层2 各神经元求偏导的值；δs（k）为误差函数对隐藏层1 各神经元求偏导的值；w3ju为输出层和隐藏层2 调整的Δ权重值；w2us为隐藏层2 和隐藏1 调整的权重值；为隐藏层1 和输入层的调整权重值；bj（k）为输出层阈值的调整值；bu（k）为隐藏层2 阈值的调整值；bs（k）为隐藏层1 阈值的调整值；η 为学习率。

由上式可知，隐藏层神经元个数可以决定深度神经网络的权重和阈值，从而决定正向传播阶段学习和反向学习阶段的性能。而在神经网络的反向误差调整中，学习率的取值和隐藏层神经元个数同样可以影响网络的收敛速度和训练结果的好坏。

3 基于遗传算法的深度神经网络优化算法

在此所提出的基于遗传算法的深度神经网优化算法GAODNN（genetic algorithm optimization deep neural network），利用遗传算法强大的全局随机搜索能力及深度神经网络挖掘特征联系能力，克服了深度神经网络中权重、阈值和学习率对网络学习的影响和陷入局部最优问题。

3.1 染色体编码

在此将深度神经网络的各隐藏层神经元、学习率和训练次数作为遗传算法的种群，然后通过浮点数编码的方式进行编码，各隐藏层神经元的区间范围为［1，100］，训练次数的区间范围为［1，50］，学习率的区间范围为［0.00001，0.05］。

3.2 适应度函数

适应度函数是遗传算法评价各个个体好坏的依据，往往会将适应度高的个体进行下一代遗传操作。在此将神经网络训练和预测后，使用二分类交叉熵作为损失函数，用所得到的准确率来定义适应度函数，公式为

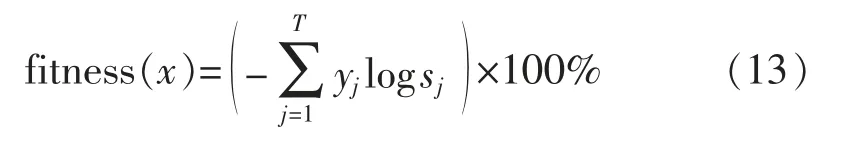
3.3 选择、交叉和变异算子

选择算子是将当前种群中选择好的个体作为父代将基因传给下一代。在此使用锦标赛选择tournament selection 算法作为遗传算法的选择策略。该算法具有更小的复杂度，易并行化处理，不容易陷入局部最优，并且不需要对所有适应度值进行排序处理。

交叉算子使用洗牌交叉算法，在交叉之前在父代中利用random.shuffle 函数进行洗牌运算，然后当在（0，1）之间产生的随机数小于所给的交叉率大小，则进行交叉变换。

在变异算子中，当在（0，1）之间产生的随机数小于所给的变异率大小，则进行变异操作。其中隐藏层神经元个数、学习率和训练次数变异的规则为

式中：c.lr 为种群中的学习率；c.maxe 为种群中的训练次数；c.Li为种群中隐藏层神经元个数，i=［1，2，…］。

3.4 GAODNN 算法描述

在此给出GAODNN 算法描述。

4 基于优化深度神经网络的入侵检测算法

根据GAODNN，提出了一种基于优化深度神经网络的入侵检测算法GAODNN-IDA （genetic algo rithm optimization deep neural network intrusion detection algorithm）。利用遗传算法的全局寻优能力和深度神经网络的特征提取能力，对入侵数据进行检测，将通过GAODNN 算法获得的DNN 各隐藏层神经元数、学习率以及训练次数，更新到基于深度神经网络的入侵检测算法中，并重新进行训练测试，通过对攻击数据和正常数据进行学习来判断入侵数据的属性。在此给出了GAODNN-IDA 算法描述。

5 试验

5.1 数据预处理

试验数据采用KDD CUP99 网络入侵数据集，该数据集约有500 万条连接数据记录，每一条数据记录包含41 个特征属性和1 个类标签属性，数据集包含4 种攻击类型和1 种正常数据标签。部分数据记录如下：

0，tcp，http，SF，239，304，0，0，0，0，0，1，0，0，0，0，0，0，0，0，0，0，10，20，0.00，0.00，0.00，0.00，1.00，0.00，0.20，121，255，1.00，0.00，0.01，0.04，0.00，0.00，0.00，0.00，normal.

0，icmp，ecr_i，SF，1032，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，511，511，0.00，0.00，0.00，0.00，1.00，0.00，0.00，255，255，1.00，0.00，1.00，0.00，0.00，0.00，0.00，0.00，smurf.

0，tcp，http，SF，54540，8314，0，0，0，2，0，1，1，0，0，0，0，0，0，0，0，0，3，3，0.00，0.00，0.00，0.00，1.00，0.00，0.00，100，100，1.00，0.00，0.01，0.00，0.01，0.01，0.01，0.01，back.

将“kddcup.data_10_percent_corrected”数据用做训练数据，将“orrected”数据用做测试数据，见表1。

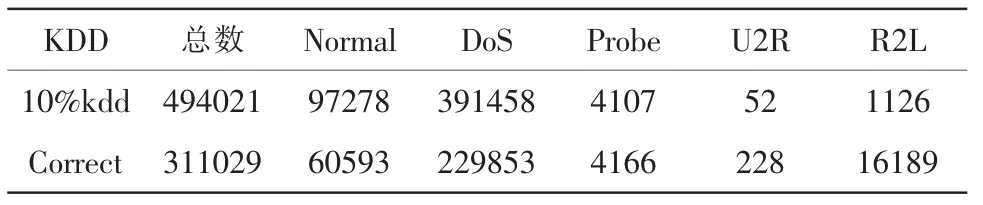
表1 KDD 数据类型Tab.1 KDD data types

由于KDD CUP99 数据集的每一个连接都由41 维特征组成，样本数据集数据非常多，因此需要从中选择合理的数据进行试验分析。文中试验根据文献[15]所提出观点，将对决策判定没有任何作用的属性删除，即删除数据集中land，urgent，su_attempted，num_outbound_cmds，is_hot_login 这5 项属性。由于该数据集每一条正常或者异常数据记录都包含41 个特征属性，大部分特征数据是数值型的，但协议名、网络服务类型和flag 标志位为非数值型，为了便于深度神经网络计算与处理，将这些非数值数据进行数值化编码。例如，对于protocol_typr 特征，其包含3 个符号即tcp，udp，icmp，将其编码为0，1，2。同理，对网络服务类型和flag 标志位进行相应的数值化处理。为了让深度神经网络更容易训练，收敛速度更快，对所有的数据按照式（15）进行归一化处理：

式中：Mmin为某一列中最小的值；Mmax为某一列中最大的值；y 为需要归一化的值。

5.2 试验环境

试验在台式计算机上完成。计算机配置如下：Inter3.50 GHz 处理器，128 GB 内存，64 位Windows 10 操作系统；编程工具为基于TensorFlow 的Keras。遗传算法相关参数设置和深度神经网络优化参数见表2，其中所有隐藏数目一致。

表2 遗传算法相关参数和深度神经网络优化参数Tab.2 Genetic algorithm related parameters and DNN optimization parameters

5.3 试验及结果分析

入侵检测指标主要有准确率AR（accuracy rate）、检测率DR（detection rate）和误报率FAR（flase alarm rate）。通过这3 个指标可以知道入侵检测方法的性能。指标的计算方法如下：

式中：TP为真正（true positive）；TN为真负（true negative）；FP为假正（false positive）；FN为假负（false negative）。

5.3.1 GAODNN-IDA 与其他DNN 的比较

为验证本文所提算法的有效性，首先给出6 种深度神经网络模型结构，隐藏层数为3 层和4 层，输入层和输出层都为1，见表3。然后，利用遗传算法对深度神经网络模型进行优化，并利用入侵检测数据集进行测试。所有的深度神经网络模型都采用relu 函数作为激活函数，该函数是一种非线性函数，可以减少采用其他激活函数导致计算量大的问题，有助于提高深层神经网络的收敛速度，降低梯度消失，加快训练速度，计算公式如下：

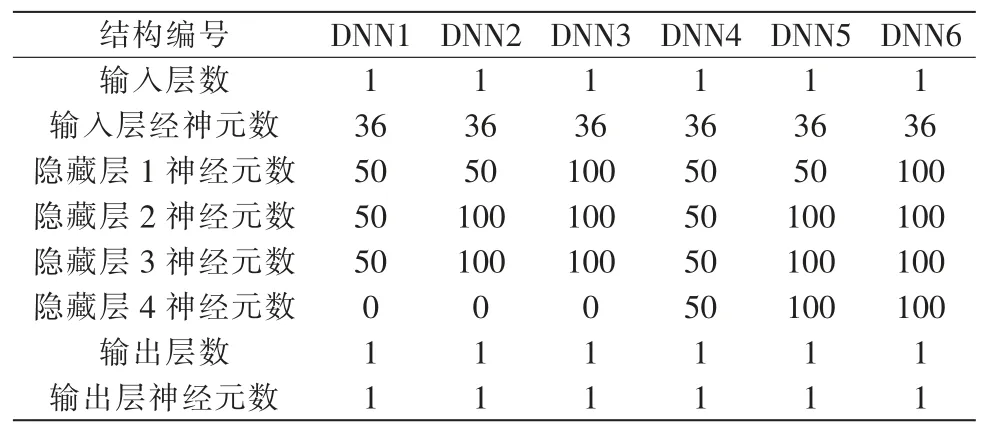
表3 深度经网络结构参数Tab.3 DNN structure parameters

所有深度神经网络模型都采用Adam 优化器，该优化器可以替代传统随机梯度下降过程的一阶优化算法，实现高效的计算，适合大规模数据；使用“binary_crossentropy”作为损失计算函数。得到的检测结果如果见表4。

表4 GAODNN-IDA 与DNN 性能对比Tab.4 GAODNN-IDA and DNN performance comparison

由表4可知，经过遗传算法优化的深度神经网络应用于入侵检测，其准确率和检测率有一定提升，误报率有一定降低。

5.3.2 GAODNN 与其他机器学习算法的比较

将本文GAODNN3-IDA 算法与典型机器学习算法应用于入侵检测并进行对比，所用数据集同样经过预处理过程，检测结果见表5。

表5 GAODNN3-IDA 与其他典型机器学习算法的性能比较Tab.5 Performance comparison between GAODNN3-IDA and other typical machine learning

由表可知，GAODNN3-IDA 算法的准确率和检测率明显高于其他典型机器学习算法，误报率明显低于其他典型机器学习算法。因此，所提出的GAODNN3-IDA 算法明显优于其他几种典型机器学习算法。

6 结语

深度神经网络算法应用于入侵检测领域，其检测性能与隐藏层的权重、 阈值和学习率密切相关。本文利用遗传算法强大的全局寻优能力，通过遗传算法的选择、交叉和变异等操作获得最优隐藏层神经元数和学习率来优化深度神经网络；将优化后的深度神经网络应用于入侵检测，对入侵数据进行学习和识别。与BP神经网络、决策树、支持向量机等算法相比，本文算法对入侵数据检测的准确率、 检测率有明显提高，误报率有明显降低。