基于网络需求度的变采样周期智能动态调度算法

时维国，雷何芬

（大连交通大学 电气信息工程学院，大连116028）

在网络控制系统NCS（network control system）中数据的传输是靠通信网络连接的，控制信号是通过网络介质发送的，网络作为数据传输的载体是一种公共资源。NCS 的性能不仅取决于控制算法，还依赖对公共系统资源的调度。若在NCS 中采用的调度方法不当，会对NCS 控制质量有很大的影响。

目前对NCS 调度方法的研究主要分为动态调度、静态调度和协同优化调度。动态调度是通过实时监测NCS 中网络资源，根据不同的需求动态的分配网络资源；静态调度是一种不会随网络变化而变化的一种离线调度。文献[1-2]采用的是动态调度算法，但未考虑网络带宽资源受限问题；文献[3-6]虽考虑了网络带宽资源受限问题，但未从变采样周期的角度考虑；文献[7-10]是在数据传输时间一定的假设条件下设计的变采样周期调度。在此，针对资源受限的NCS，同时考虑了网络数据传输时间的不确定性，从变采样周期的角度设计一种动态调度算法。为使NCS 控制性能最优，在预测网络利用率时，利用变步长自适应最小均方LMS（least mean square）滤波算法预测控制回路中数据包的传输时间，同时采用模糊神经网络算法动态的确定各回路的网络需求度，根据预测的网络利用率动态的分配各网络回路的带宽和调整各回路的采样周期。

1 网络控制系统结构

针对具有多个控制回路的NCS 结构如图1所示，其中包括了一个网络调度器和多个控制回路。

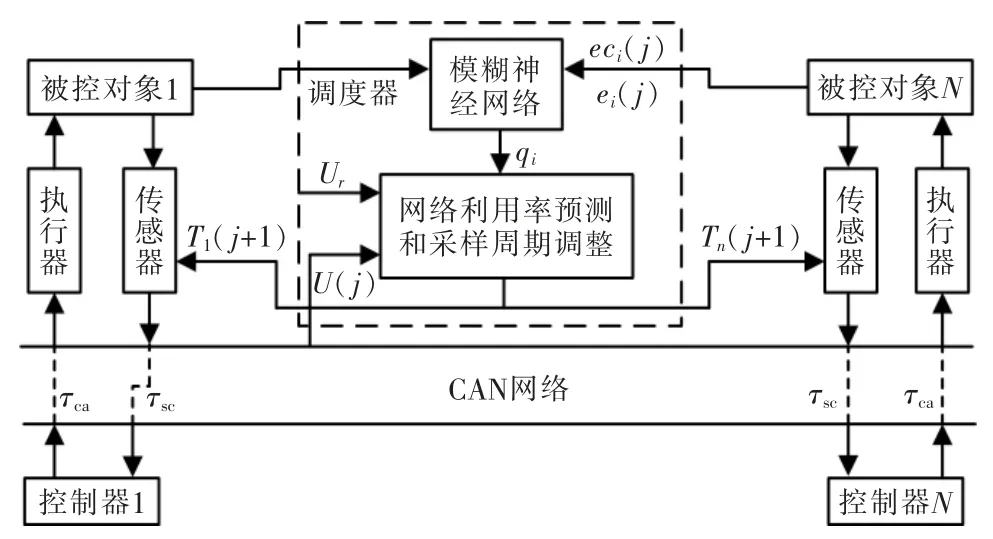
图1 NCS 调度策略结构Fig.1 NCS scheduling strategy structure

图中，NCS 中各个控制回路之间相互独立，网络调度器采用时间驱动方式，周期性的采集网络状态和回路状态。调度器利用模糊神经网络算法根据各回路的误差和误差变化率，给出每个网络控制回路的网络需求度，结合预测的下一时刻各网络控制回路的网络利用率和数据包的传输时间，动态的调节各网络控制回路的下一时刻的采样周期。

2 网络需求度计算

根据各网络控制回路的误差和误差变化率来描述各回路的网络需求度，采用神经网络的模糊系统求取网络控制回路各网络需求度。

模糊推理采用的是双输入单输出的二维模糊控器。以第i 个控制回路为例，以控制回路的误差ei（k）和误差变化率eci作为输入变量，以控制回路的网络需求度qi作为输出。有

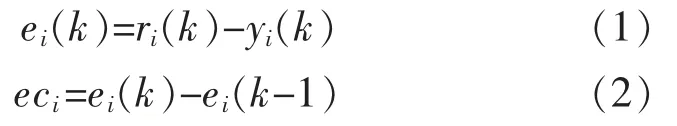
式中：ri（k）为k 时刻第i 回路的参考输入；yi（k）为k时刻第i 回路的输出。

输入的模糊子集E=｛NB，NM，NS，ZE，PS，PM，PB｝，EC=｛NB，NS，ZE，PS，PB｝；输出的模糊子集Q=｛PS，S，M，B，PB｝。控制回路的误差和误差变化率范围为［-1，1］，输出的量化等级为5 级［1，2，3，4，5］。两输入的量化等级为9 级［-4，-3，-2，-1，0，1，2，3，4］，取量化因子ke=5，kec=4，比例因子为0.2。选取三角形隶属度函数作为输入变量的隶属度函数，梯形隶属度函数作为输出变量的隶属度函数。模糊控制规则见表1。

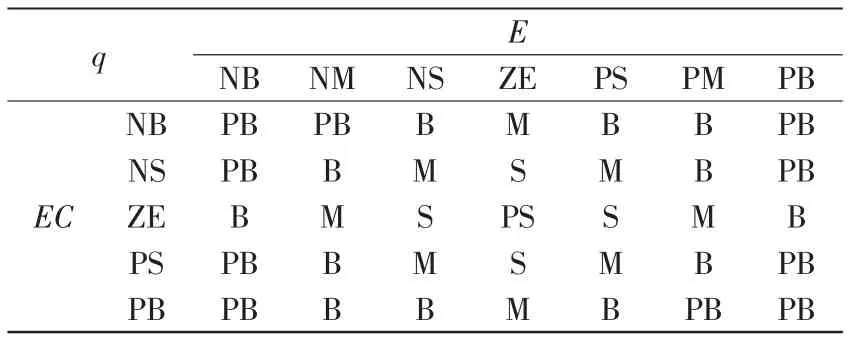
表1 模糊控制规则Tab.1 Fuzzy control rules

根据对NCS 控制性能的分析，建立模糊控制规则：误差ei数值越大，则表明该控制回路现有的网络带宽资源不能满足数据的传输，需要增加的该控制回路的网络带宽以提高该控制回路的控制性能，即需要被定义比前一时刻大的网络需求度；如果误差ei和误差变化率eci相乘结果为正数，则说明该控制回路的误差有增大的趋势，该控制回路应赋值比前一时刻更大的网络需求度；如果误差ei和误差变化率eci相乘结果为负数，则说明该控制回路误差有减小的趋势，该控制回路应赋值比前一时刻较小的网络需求度。

网络需求度qi根据神经网络记忆模糊规则的方法[11]求出，神经网络选用经典的BP 神经网络，以误差ei和误差变化率eci建立的模糊子集作为神经网络输入，输出空间对应以网络需求度qi的模糊子集中的量化值作为输出。其网络需求度模块Simulink的仿真建模如图2所示。

图2 网络需求度模块Fig.2 Network requirements module

3 网络利用率预测

NCS 中网络利用率为

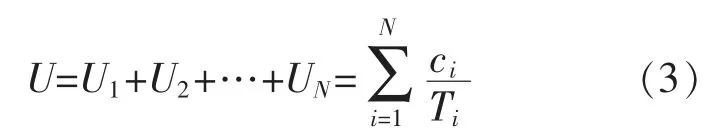
式中：Ui为第i 个回路的网络利用率；N 为系统中回路的数目；ci为第i 个回路中任务信息的传输时间；Ti为第i 个回路任务的采样周期。

为使网络利用率达到期望值，采用反馈控制的方法，网络利用率预测结构如图3所示。

图3 网络利用率预测结构Fig.3 Network utilization prediction structure

第j+1 个采样周期系统总的网络利用率为

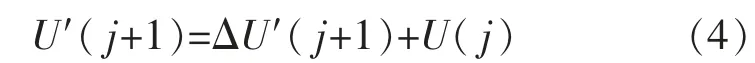
式中：U（j）为网络利用率的真实值；Ur为网络利用率的期望值；Ku为比例控制增益。

为确保网络利用率能够收敛到期望值，在比例调节的过程中，应满足

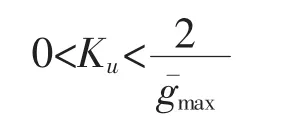
4 变采样周期调整

对于数据传输时间，很多研究都将其假定为固定值，但它实际上是随网络负载和传输路径等条件而随机变化的。数据包传输时间可根据历史数据进行预测，在此采用变步长自适应LMS 滤波算法预测控制回路中数据包的传输时间。利用调度器中存储的N 个时刻的回路时延组成的时延向量为

则k 时刻的时延估计值为

式中：权重W（k-1）为k-1 时刻自适应滤波器的权系数。采用变步长自适应LMS 滤波算法[12]调节，即

式中：e（k）为k 时刻回路误差；c（k-1）为k-1 时刻的回路时延期望值；（k-1）为k-1 时刻的回路时延的实际值；C（k-1）为k-1 时刻时延向量；u 为控制稳定性和收敛速度的参数。

用新测得的时延值更新调度器中存储的过去N个时刻的历史时延值建立时延向量，同时不断更新权重矩阵，其中α 和β 值控制着收敛速度。利用时延向量和权重矩阵计算控制回路系统输出，新计算得到的当前采样时刻即为的网络时延的估计值。

由式（3）可得控制回路的采样周期计算公式为

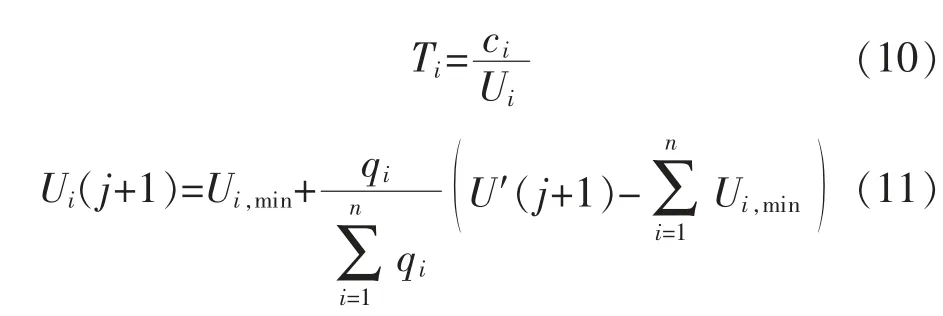
其中

式中：ci为回路i 中数据的传输时间；Ui，min为NCS稳定的最小网络利用率；Ti，max为NCS 稳定的最大采样周期。网络利用率根据各控制回路的网络需求度，采用线性分配算法。故

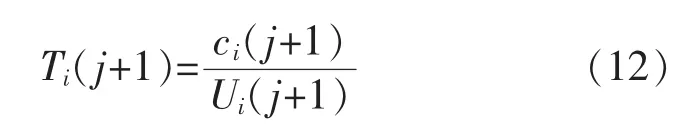
5 仿真试验及分析

本试验模型在MatLab/Simulink 仿真平台和True Time 工具箱下搭建，对三回路NCS 进行调度仿真。每个控制回路均由传感器节点、控制器节点、执行器节点和被控对象等组成，被控对象的传递函数为

控制器采用PID 控制算法，取比例因子K=1，微分系数Td=0.94，积分系数Ti=0.12。CAN 网络数据传输速率为0.5 Mb/s，数据包大小为80 bit，其中干扰节点占用的网络带宽为20%，网络利用率设定值Ur=80%。控制回路1 初始采样周期取h1=8 ms；控制回路2 初始采样周期取h2=10 ms；控制回路3初始采样周期取h3=12 ms。

同时，对EDF 调度策略下固定采样周期和本文所设计的变采样周期算法进行仿真，对应的各回路的响应曲线如图4所示。由图可见，相比较固定采样周期下的NCS 各控制回路响应曲线，对应变采样周期的NCS 各控制回路响应曲线具有一定的稳定性能。

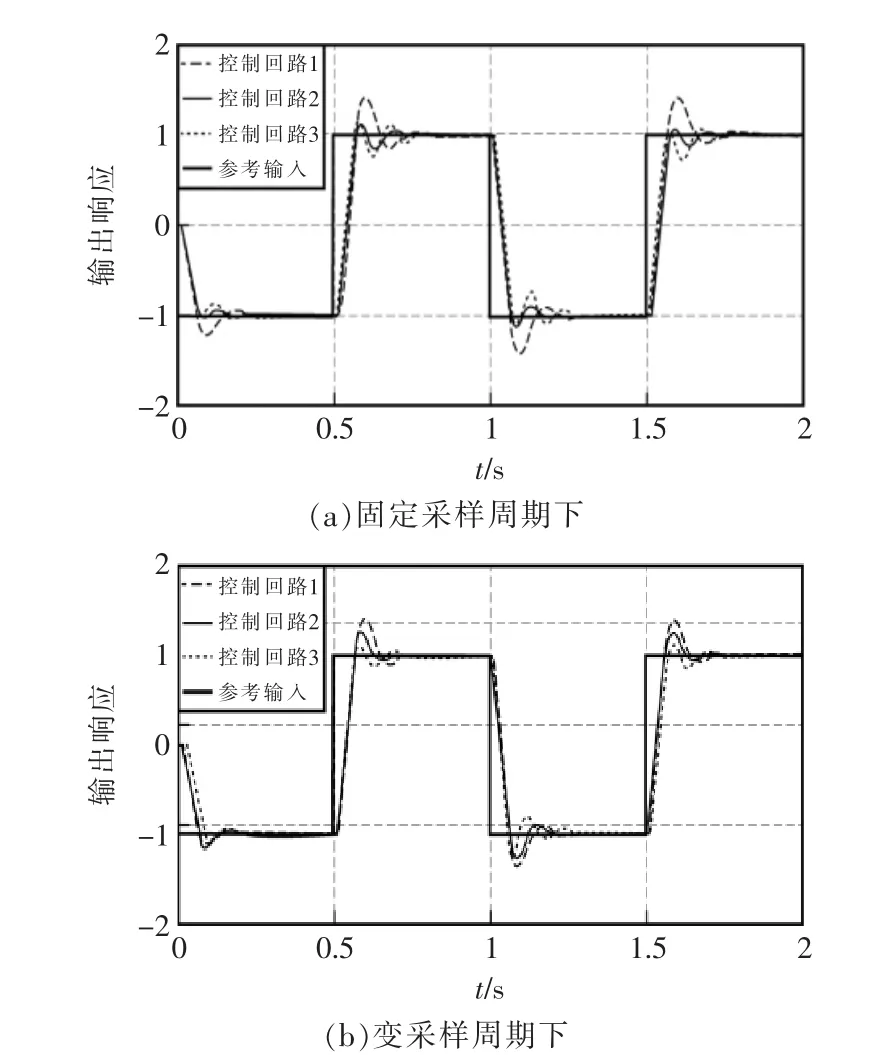
图4 固定采样周期与变采样周期的EDF 回路输出响应曲线Fig.4 Output response curve of EDF loop with fixed sampling period and variable sampling period

通过对各个回路的绝对误差积分IAE（integral of absolute error）的计算，如图5所示。由图可见，在变采样周期的调度下相比固定采样周期，3 个控制回路的IAE 值有一定的减少。

图5 EDF 固定采样周期与变采样周期的三回路IAE 值Fig.5 Three-loop IAE value of EDF fixed sampling period and variable sampling period

6 结语

针对资源受限NCS，提出了基于网络需求度的一种变采样周期动态调度算法，以各个控制回路的误差和误差变化率建立网络需求度，对网络资源实时分配，实时调整控制回路的采样周期。仿真结果表明了该预测方法的有效性，通过变采样周期调度算法能保证系统的控制性能及系统的稳定性，并使系统控制性能有一定的提高。