SABRE空气预冷器流动与换热数值研究
2019-11-05刘天依吉洪湖
魏 鑫,金 峰,刘天依,吉洪湖
(南京航空航天大学 能源与动力学院,江苏 南京 210016)
0 引言
协同吸气式火箭发动机(SABRE)在高马赫数飞行时,因进气滞止温度过高,空气难以压缩,动力系统性能会急剧下降。为了改善吸气式动力系统高飞行马赫数时的性能,通过在进气道中加预冷器,以降低进气温度,减小压气机功率,这对扩展飞行器飞行包线、提高发动机推重比具有重要意义[1-5]。SABRE在氢气和空气之间引入闭式氦气循环,借助低温氦气来冷却高温空气[6-8],在较短的时间内实现空气和低温氦气高效换热,大温差、高效紧凑、轻质的空气预冷器是协同吸气式火箭发动机的核心技术[9-10]。
目前,SABRE型发动机方案已经从SABRE3发展到SABRE4,相比之下,后者优化了循环方式,方案可行性大大增加。SABRE3型预冷器目前存在一些工程性问题,如:空气冷却到-150 ℃会结霜阻塞通道,增设除霜装置会使得预冷器结构复杂、重量增加;预冷器的长度、体积限制使得预冷器难以达到换热要求。因此,在SABRE3方案基础上,2015年,REL(Reaction Engines Ltd)公司公布了优化后的“佩刀”发动机方案,即SABRE4[11-12],SABRE4预冷换热器在Ma=1.9~2.8仅预冷器HX1工作,在Ma=2.8以上预冷器HX1和HX2两者同时工作[13]。预冷换热器出口温度由SABRE3的-150 ℃提高到0 ℃以上,省去了结霜控制系统。
针对SABRE型发动机空气预冷器,国内外学者做了许多研究。最初,基于“佩刀”发动机先进的预冷概念,在上世纪90年代,布里斯托尔大学研制了由直径0.38 mm微细管组成的实验型预冷器模块JMHX[14-15],研究了JMHX冷却剂为氦气、氮气时在不同流量下的换热性能,并分析了经典理论中摩擦因子和传热系数的公式在微通道换热器中的适用性。Helen Webber[16]实验研究了与SABRE预冷器相似的叉排布局圆柱管束在低速风洞下的对流换热能力,同时测得了空气流过圆柱管束时的流场特性。Huan Lee[17]建立了紧凑式换热器性能试验台,对紧凑式换热器进行了性能测试,初步实验结果表明该换热器具有优良的性能,实验结果与设计值吻合较好。李晨沛[18]针对复合发动机的预冷器,研究管内流体速度、管外流体速度、入射角度以及管间距对于空气侧换热性能的影响机制,结果表明:通过增大管内制冷介质的流量,缩小管间距以及空气垂直入射角度等均能提高预冷器换热效率。程惠尔[19]通过对选定参数的空气预冷换热器作了全工况跟踪计算,给出了空气通道阻力特性的数值结果。
综上,国内外学者通过实验、数值模拟、一维分析的方法针对预冷器做了一些研究,但研究对象大部分是传统的叉排直管束,对于SABRE特殊形式的预冷器,由于结构形式复杂,对其流动换热规律研究很少。为了深入研究空气预冷器的流动换热特性,本文针对SABRE型发动机预冷器,建立预冷器流动换热的最小周期性模型,研究了管间距、管排数、空气入射角度及氦气/空气热容量比对于预冷器流动换热的影响规律,为空气预冷器的工程设计提供参考。
1 物理模型和计算方法
1.1 物理模型和网格划分
图1为空气预冷器结构示意图,空气预冷器由弯曲状的预冷片、总管及支管组成,共36个预冷片,预冷片绕圆心旋转形成辐射状排布。低温高压的氦气从内环的总管流入,之后流入每根支管,支管连接着预冷片,每个预冷片由四排毛细管组成叉排管阵,高温空气流经管与管之间的缝隙逐渐被冷却。由于预冷器在圆周方向具有周期性重复的特点,氦气和空气的流动换热也具有周期性重复的特点,对于预冷器的最小周期性单元,其流动换热能够代表整个预冷器的流动换热,因此可以取最小的周期性计算单元(图1黄色扇形区域)进行研究。
图2为预冷器计算单元模型,计算单元内径873 mm,外径1 250 mm。每一排预冷片都是由4排毛细管组成的,毛细管外径1 mm,壁厚0.05 mm。管排数为预冷器计算单元内空气流过的预冷片数目,管阵叉排布局以等边三角形布置,管间距为相邻两个毛细管圆心之间的距离。氦气在1和1’,2和2’,3和3’,…,8和8’的流动状态相同,每根管子的出口都是旋转对应的下一排管子的入口,氦气在计算域中往返流动,计算域内的毛细管可以等效为一根完整的毛细管。计算单元内扇形夹角为10°,由于夹角相对较小,空气在扇形区域上下边界处空气的流动可以近似看成相同的。为了减少计算量,简化计算结构,预冷器轴向选择四根半管作为轴向的最小周期性单元,同时体现了叉排布局结构,对于四根半管的截面,设为对称边界条件,使得半管的流动状态与完整管相似。
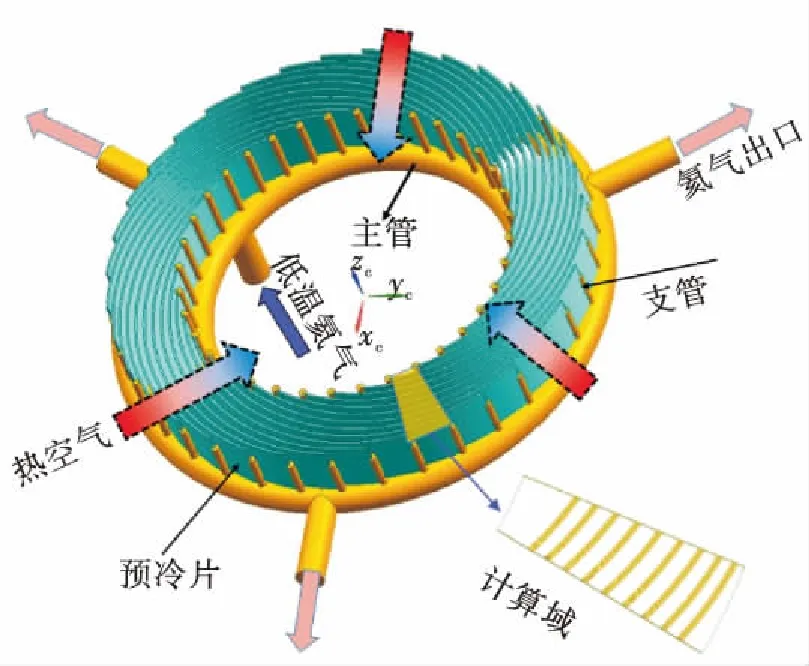
图1 空气预冷器模型Fig.1 Model of air precooler
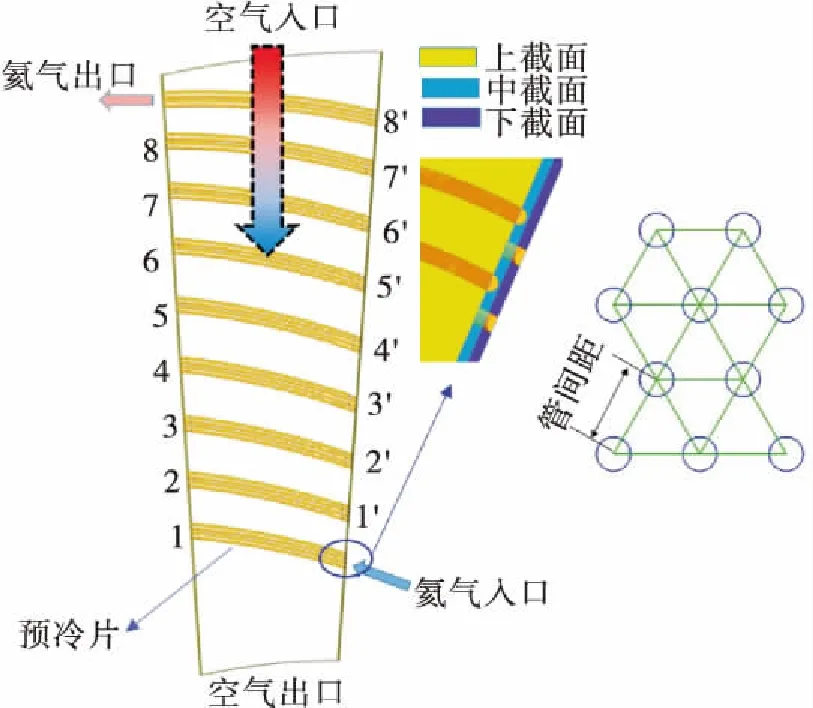
图2 预冷器计算单元模型Fig.2 Computational model of air precooler
本文采用ICEM软件对预冷器计算模型进行网格划分,管内外都设置边界层网格,空气侧第一层网格高度为0.002 8 mm,增长比率1.3,共10层,氦气侧第一层网格高度为0.001 1 mm,增长比率1.1,共10层,管内外壁面第一层网格y+<5。同时对计算模型进行网格独立性验证,当网格量大于870万时,空气侧出口温度基本不随网格量变化。
1.2 边界条件和计算方法
计算模型空气入口采用压力入口边界条件,给定总温总压,空气出口采用压力出口,并给定出口目标流量。氦气入口选择速度入口边界条件,入口静温为340 K,氦气出口采用压力出口边界条件,给定出口静压20 MPa。周向两侧壁面除了氦气入口和氦气出口外均设为周期性边界条件,上下截面设为对称边界条件,管壁设为耦合壁面。由于氦气在SABRE发动机中为闭式循环[20],氦气总流量为定值。根据文献[21]可知,SABRE预冷器空气侧流量随飞行弹道基本保持不变。因此在设置边界条件时考虑到了预冷器空气和氦气流量恒定的工作特性,并且预冷器总长度设定为定值4 m,氦气和空气总的流量保持不变,其中
(1)
(2)
式中:mHe为预冷器计算单元氦气流量;MHe为预冷器的氦气总流量;mAir为预冷器计算单元空气流量;MAir为预冷气的空气总流量;w为管间距;l为预冷器长度。
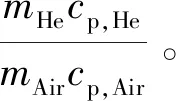

表1 预冷器计算单元的研究变量取值
本文采用Fluent16.0进行数值模拟计算,数值模拟中空气和超临界氦气的物性参数由NIST软件查得,空气设为理想气体,比热容、粘性系数及导热率采用多项式函数进行拟合,由于超临界氦气在毛细管内部流阻很小,压力变化很小,超临界氦气密度设为温度的函数。
1.3 数值方法验证
参考文献[14]验证数值计算方法,文献对紧凑型预冷器模块JMHX进行了实验研究,JMHX外形结构为40 mm×40 mm×40 mm大小,共415个直径0.38 mm的微细管束,呈10排83列排布,管内冷却介质为低温高压氦气或者氮气。选择文献中内部介质为氦气、热容量比为1的实验进行对比分析,图3为不同湍流模型下各排管氦气出口温度计算结果与实验结果比较,可以发现,靠近空气入口的前几排管束计算结果与实验结果误差较大,后几排管束的温度计算结果与实验结果误差较小,这可能是因为前面的管排管内外介质温差较大,毛细管的热缩性较大,几何尺寸变化较大,而数值模拟结果没有考虑形变的影响,因此前几排的误差较大,相比来看,SST-kω湍流模型比其他湍流模型更接近实验结果,因此本文数值计算选择SST-kω湍流模型。
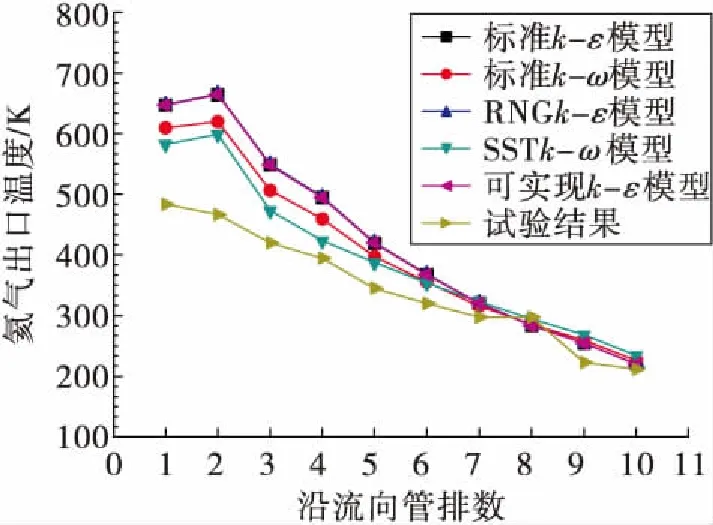
图3 不同湍流模型下各排管氦气出口温度数值结果与实验结果比较Fig.3 Comparison of helium outlet temperature between numerical results and experimental results with different turbulence models
2 计算结果与讨论
当氦气压力大于临界压力(0.228 MPa),氦气温度大于临界温度(5.19 K),此时氦气状态为超临界状态[22]。预冷器毛细管内氦气压力远大于临界压力,温度远大于临界温度,因此预冷器内氦气为超临界状态。超临界氦气为单相[23],不会因为温度升高而呈现两相状态,因此本文预冷器管内超临界氦气属于单相换热范畴。
2.1 管间距对于预冷器流动与换热的影响
针对管间距对于预冷器流动与换热的影响,本文研究了来流工况不变的条件下,管间距对于空气侧总压损失系数以及空气侧、氦气侧平均换热系数的影响规律。
预冷器空气侧总压损失系数定义为
(3)
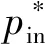
氦气侧平均换热系数基于管内湍流对流换热实验关联式Dittus-Boelter公式可得
(4)
空气侧平均换热系数[24],通过以下方法计算。预冷器在传热达到稳态后,换热量
Q=mAircp,AirΔTAir=mHecp,HeΔTHe
(5)
式中ΔTHe和ΔTAir为氦气、空气进出口温差,预冷器总传热系数为
(6)
式中:A为预冷器的壳侧换热面积;(ΔTm)ctf为将给定的冷热流体的进出口温度布置为逆流时的对数平均温差;ψ为小于1的修正系数,ψ的计算参考文献[25],根据预冷器流体流动形式,选择n个相同的叉流热交换器流动形式计算ψ值,经计算ψ的范围为0.98~1,说明预冷器流体流动形式接近逆流布置。基于壳侧换热面积的总传热系数[26]
(7)
式中do和di为管外径和管内径。由于毛细管壁厚很薄,导热热阻Rw以及污垢热阻RS忽略不计,可以计算得空气侧平均换热系数
(8)
图4为预冷器空气侧总压损失系数随管间距变化关系,可以看出,随着管间距从1.5 mm增大到3.5 mm,总压损失系数从2.6%降低到0.5%,且随着管间距增大,总压损失系数下降速率减缓。
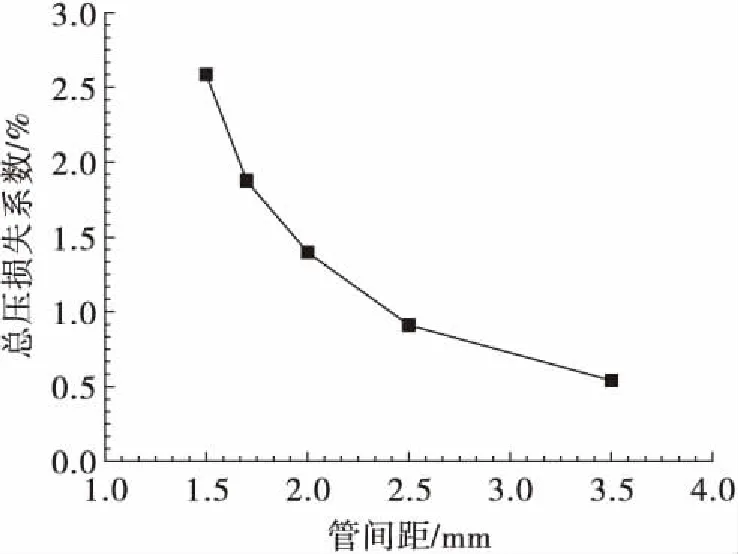
图4 预冷器空气侧总压损失系数随管间距变化关系Fig.4 Effects of tube pitch on total pressure loss coefficient of air side
横掠管束压降经验关系式[25]
(9)
其中
Re=ρVmaxD/μf
式中:N为管排数;D为管外径;μf为管壁平均温度;Vmax为管束间的最大速度;Vf为来流速度;s1为管间距。当管间距变化时,空气来流速度基本不变,管束间的最大速度变化较大,而定性温度下的物性参数变化很小,因此压降主要与管束间的最大流速有关,且压降变化趋势与最大流速变化趋势相同,压降近似与管束间最大流速的1.8次方成正比。
图5为预冷器空气侧、氦气侧平均换热系数随管间距变化关系,随着管间距从1.5 mm增大到3.5 mm,空气侧平均换热系数增大了约4.4倍,氦气侧平均换热系数增大了约2倍,管内外对流换热能力增强,可以看出,氦气侧换热系数远大于空气侧换热系数。预冷器氦气和空气总流量不变,在给定预冷器长度不变的约束下,随着管间距增大,氦气入口流速增大,雷诺数增大,而流体普朗特数(Pr)变化很小,根据管内换热关联式(4),氦气侧平均换热系数增大;而空气侧平均换热系数主要由预冷器总体换热系数决定,随管间距增大,预冷器换热面积与对数平均温差乘积的减小速率大于换热功率的减小速率,根据总体换热系数的表达式(6),总体换热系数增大,空气侧平均换热系数因而增大。
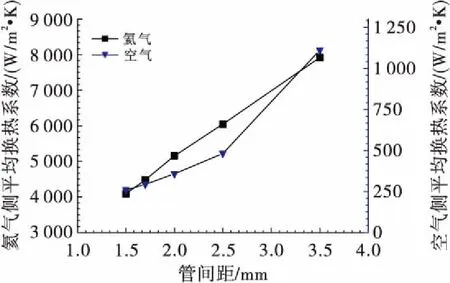
图5 预冷器空气侧、氦气侧平均换热系数随管间距变化关系Fig.5 Effects of tube pitch on heat transfer coefficient of both sides
图6为预冷器空气出口温度和预冷器换热功率随管间距变化关系,随着管间距从1.5 mm增大到3.5 mm,空气出口温度升高,氦气出口温度降低,换热功率降低了31%,预冷效果减弱。虽然减小管间距会降低预冷器空气侧、氦气侧换热系数,但预冷器总换热面积增大了,而空气、氦气总流量不变,因此减小管间距能够提高预冷效果,降低空气出口温度。
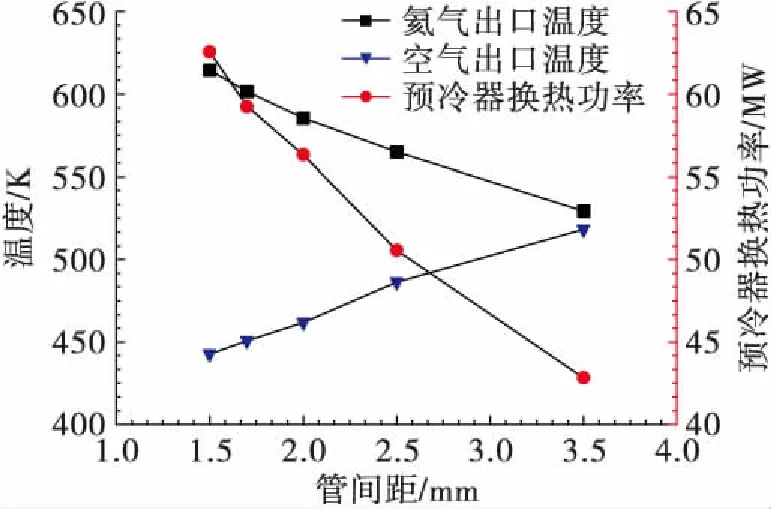
图6 预冷器空气出口温度和预冷器换热功率随管间距变化关系Fig.6 Effects of tube pitch on air outlet temperature and heat transfer power
2.2 管排数对于预冷器流动与换热的影响
针对管排数对于预冷器流动与换热的影响,本文研究了来流工况不变的条件下,管排数对于空气侧总压损失系数以及空气侧、氦气侧平均换热系数的影响规律。
图7为预冷器空气侧总压损失系数随管排数变化关系。可以看出,随管排数从7排增大到15排,预冷器空气侧总压损失系数从1.5%增大到了7%,且近似呈线性上升。管间距不变,由于空气侧流量为定值,侧管束间的最大速度不变,定性温度下的物性参数也基本不变,由横掠叉排管束压降经验关系式(9)可知,空气侧压降与管排数呈线性关系,因此预冷器空气侧总压损失系数随管排数增大近似线性上升。
图8为预冷器空气侧、氦气侧平均换热系数随管排数变化关系,随管排数从7排增大到15排,空气侧平均换热系数减小了57%,氦气侧换热系数略微减小,减小幅度小于4%。随管排数增大,对数平均温差与换热面积乘积的增大速率大于换热功率增大的速率,根据总体换热系数的表达式(6),总体换热系数减小,空气侧平均换热系数因而减小。氦气侧平均换热系数主要由雷诺数决定,随管排数增大,氦气侧Pr数基本不变,而雷诺数略微减小,根据管内换热关联式(4),氦气侧平均换热系数略微减小。
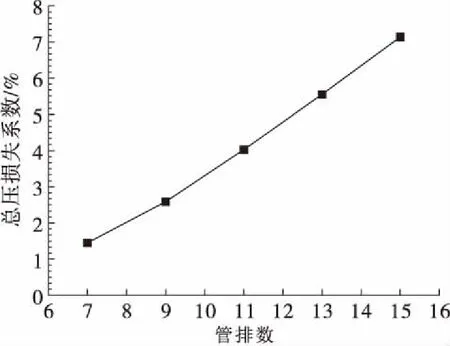
图7 预冷器空气侧总压损失系数随管排数变化关系Fig.7 Effects of row number on total pressure loss coefficient of air side
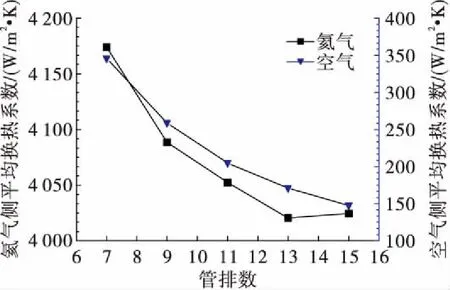
图8 预冷器空气侧、氦气侧平均换热系数随管排数变化关系Fig.8 Effects of row number on heat transfer coefficient of both sides
图9为预冷器空气出口温度和预冷器换热功率随管排数变化关系,随管排数从7排增大到15排,空气出口温度降低,氦气出口温度升高,预冷器换热功率增大了20%,预冷效果增强;同时可以看出,随管排数增大,预冷器换热功率上升速度减缓,空气出口温度下降速度减缓,说明增大管排数对于空气预冷效果的收益减小,因此管排数不宜过多。
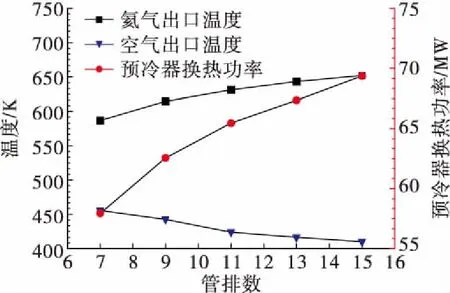
图9 预冷器空气出口温度和预冷器换热功率随管排数变化关系Fig.9 Effects of row number on outlet temperature and heat transfer power
2.3 空气入射角度对于预冷器流动与换热的影响
针对空气入射角度对于预冷器流动与换热的影响,本文研究了来流总温、总压不变的条件下,空气入射角度对于空气侧总压损失系数以及空气侧、氦气侧平均换热系数的影响规律。
图10为空气侧总压损失系数随空气入射角度的变化关系,在空气入射角度小于90°时,入射角度对于空气侧总压损失系数的影响较小,总压损失系数变化小于5%;空气入射角度大于90°时,随着入射角度增大,空气侧总压损失系数逐渐增大,入射角度从90°增加到150°,空气侧总压损失系数增大了20%。
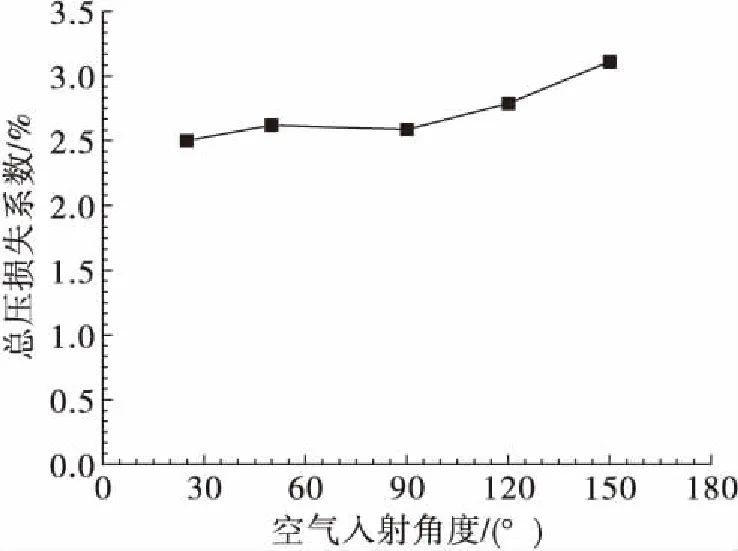
图10 空气侧总压损失系数随空气入射角度的变化关系Fig.10 Effects of incidence angle on total pressure loss coefficient of air side
总压损失系数随空气入射角度变化趋势不同的原因可以从图11中分析得到,图11为不同入射角度下预冷器计算单元中截面流场图,从图11可以看出,空气在流经第三排管阵后流动得到充分发展,空气流动方向趋于稳定,且充分发展后的空气流动方向基本不随空气入射角度发生改变。在入射角度小于90°时,空气流过前3排管阵时空气流动方向偏转角度较小,因此总压损失变化较小;而当入射角度大于90°时,随入射角度增大,空气流过前3排管阵时空气流动方向偏转角度逐渐增大,因此总压损失逐渐增大。同时从图11中还可知,入射角度小于90°时,随入射角度增大,空气入口速度逐渐减小;入射角度大于90°时,随入射角度增大,空气入口速度增大。这是因为预冷器空气入口流量不变,垂直于进口曲面的速度分量Vn不变,空气入口速度V=Vn/sinθ,因此随入射角度增大,空气入口速度先减小后增大。

图11 不同入射角度下预冷器计算单元中截面流场图Fig.11 Flow field of middle section under different incidence angles
图12为预冷器空气侧、氦气侧平均换热系数随空气入射角度变化关系,可以看出,空气入射角度对于空气侧、氦气侧换热基本没有影响。从图11可知,空气在流过管阵充分发展后,流场基本不随空气入射角度发生变化,因此空气入射角度对于换热的影响很小。
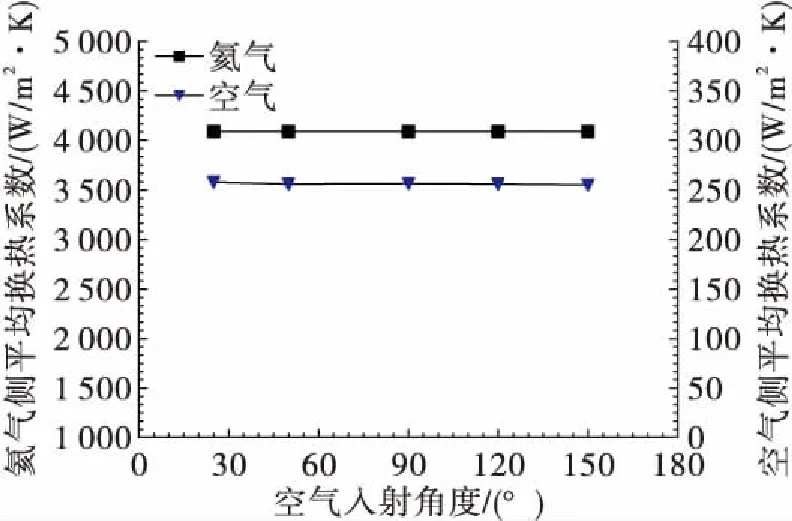
图12 预冷器空气侧、氦气侧平均换热系数随空气入射角度变化关系Fig.12 Effects of incidence angle on heat transfer coefficient of both sides
2.4 氦气/空气热容量比对于预冷器流动与换热的影响
针对氦气/空气热容量比对于预冷器流动与换热的影响,本文研究了来流总温、总压以及空气侧流量不变的条件下,改变氦气总流量,也就是改变氦气/空气热容量比对于空气侧总压损失系数以及空气侧、氦气侧平均换热系数的影响规律。
图13为空气侧总压损失系数随氦气/空气热容量比的变化关系,随着氦气/空气热容量比从1.06增大到1.64,空气侧总压损失逐渐下降,总压损失下降了13%。这是因为管内氦气流量增加使得空气侧预冷效果增强,空气温度降低,空气密度进而增大,而预冷器空气侧流量不变,因而沿程空气流速降低,使得空气侧总压损失减小。
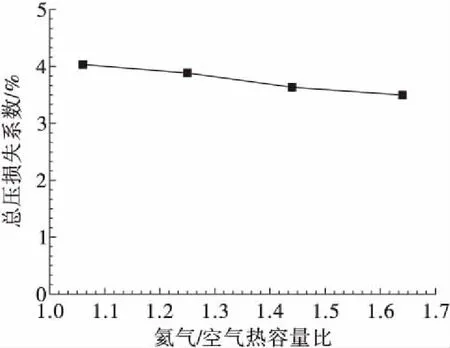
图13 空气侧总压损失系数随氦气/空气热容量比的变化关系Fig.13 Effects of heat capacity ratio on total pressure loss coefficient of air side
图14为预冷器空气侧、氦气侧平均换热系数随氦气/空气热容量比变化关系,随着氦气/空气热容量比从1.06增大到1.64,空气侧平均换热系数增大了30%,氦气侧平均换热系数增大了40%。氦气/空气热容量比增大,也就是氦气入口流速增大,使得管内氦气雷诺数增大,而氦气Pr数基本不变,根据换热关联式(4),氦气的平均换热系数增大。空气侧平均换热系数增大是因为换热功率增大,对数平均温差减小,根据总体换热系数表达式(6),总体换热系数增大,空气侧换热系数也增大。
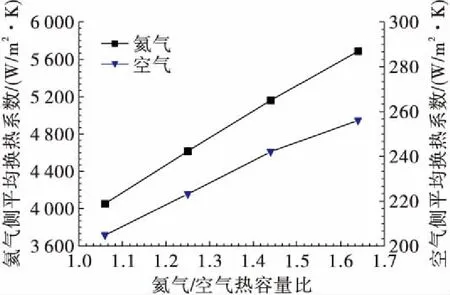
图14 预冷器空气侧、氦气侧平均换热系数随氦气/空气热容量比变化关系Fig.14 Effects of He/Air heat capacity ratio on heat transfer coefficient of both sides
通过以上对空气预冷器空气侧与氦气侧流动换热的基本特性数值研究,揭示了预冷器管间距、管排数、空气入射角度、氦气/空气热容量比对于预冷器流动换热的影响规律,可以为设计同类型空气预冷器的实际工程设计提供可靠的技术基础。
3 结论
1)随着管间距从1.5 mm增大到3.5 mm,总压损失系数从2.6%降低到0.5%,且随着管间距增大,总压损失系数下降速率减缓;空气侧平均换热系数增大了约4.4倍,氦气侧增大了约2倍,但换热功率降低了31%,空气出口温度升高,预冷效果减弱。
2)随着管排数从7排增大到15排,预冷器空气侧总压损失系数从1.5%增大到了7%,且近似呈线性上升。空气侧平均换热系数减小了57%,氦气侧减小了4%。预冷器换热功率增大了20%,预冷效果增强。
3)在空气入射角度小于90°时,入射角度对于空气侧总压损失系数的影响小于5%;空气入射角度大于90°时,随着入射角度增大,空气侧总压损失系数逐渐增大,入射角度从90°增加到150°,空气侧总压损失系数增大了20%;空气入射角度对于空气侧、氦气侧换热几乎没有影响。
4)随着氦气/空气热容量比从1.06增大到1.64,空气侧总压损失下降了13%,空气侧平均换热系数增大了30%,氦气侧平均换热系数增大了40%,预冷效果增强。
