翼型气动优化设计问题多极值特性研究

何萌，白俊强，昌敏，张煜

(1.西北工业大学 航空学院，西安 710072) (2.西北工业大学 无人系统技术研究院，西安 710072)

0 引 言

飞行器气动外形优化研究已取得了显著的成果，通过采用优化算法，能够设计出高性能的翼型，甚至能进行复杂全机构型的设计。影响飞行器气动外形优化效率[1]的两个主要因素为计算流体力学(Computational Fluid Dynamics，简称CFD)和优化算法，目前CFD作为一项成熟的技术已广泛的应用于工程应用当中，而优化算法仍然有很大的发展空间。优化算法的合理选择依赖于优化问题，必须考虑设计变量的类型(例如离散和连续)、约束的数量、设计空间的特点(一般来说，对于大部分优化问题，设计空间是光滑的)。

目前常用的优化算法[2]可以分为两类：一类是基于梯度的优化算法，这类算法需要目标函数的梯度信息，例如最速下降法、序列二次规划算法(Sequential Quadratic Programming，简称SQP)等；另一类是全局优化算法，这类算法只需要目标函数值，而不需要目标函数的梯度信息，例如粒子群算法、遗传算法以及直接搜索算法等。全局算法耗时长，理论上其优化过程的极限可以收敛到全局最优解，优化效果比梯度算法好，但基于梯度的优化算法通常能迅速收敛到局部最优解。若气动优化问题是一个高度非线性、多峰值的问题，基于梯度的优化算法在求解这类问题时对初始设计点的选择有很强的依赖性，难以获得全局最优解。如果气动优化问题是一个单峰值问题，则梯度算法能够得到相对满意的最优解，并且有更高的优化效率。因此，对气动外形优化问题设计空间的多极值特性有所了解是十分必要的，有助于我们在翼型设计阶段合理选择优化算法，提高飞行器气动外形优化效率，缩短飞行器设计周期。

在一些气动外形优化问题中，多极值特性是存在的，例如H.P.Buckley等[3]研究表明在翼型多点优化时出现两个局部最优点；J.E.Hicken等[4]优化结果表明机翼展向垂直方向外形优化至少有两个局部最优点，即上翘小翼和下翘小翼；而Lü Zhoujie等[5]探索了CRM(Common Research Model)机翼优化问题的多极值特性，其研究结果证明CRM机翼单点优化问题是单极值问题；O.Chernukhin等[1]探究了翼型和矩形机翼在定升力减阻优化问题中的多极值特性，结果表明，翼型优化在其给定的设计状态和约束下是一个单极值问题(优化问题没有考虑力矩约束的影响)，而机翼外形优化存在多极值特性；N.P.Bons等[6]研究了ADODG(Aerodynamic Design Optimization Discussion Group) case 6的多极值特性，发现机翼气动外形优化结果取决于诱导阻力和粘性阻力之间的权衡。但上述研究对翼型在跨声速气动优化过程中的多极值特性探究较少，对优化中变量设计空间的认识并不明晰，缺少梯度算法和全局算法的优化效率和结果的详细对比。

本文主要使用自由变形方法(Free-Form Deform，简称FFD)、基于伴随的梯度优化算法、全局类优化算法探索ADODG case 2中 RAE2822翼型单点优化问题的多极值特性，并分析如果在设计空间中单极值存在的条件下，全局算法是否还有其优势。

1 数值求解方法

本文使用RANS方程求解器进行定常求解。三维非定常雷诺平均N-S方程的控制方程为

(1)

式中：Q为守恒向量；Fc为对流矢通量；Fv为粘性通量。

空间离散格式为中心格式，优化时采用S-A(Spalart-Allmaras)模型作为湍流模型。

2 参数化方法及网格变形方法

采用FFD参数化方法[7]，在需要被参数化的几何外形周围建立FFD控制体，通过对FFD控制体顶点的移动，实现对FFD控制体中的目标几何体上的变形。FFD参数化方法能以较少的设计变量光滑地描述曲线、曲面、三维几何体的几何外形，并能方便地应用于局部外形修型设计。对于本文的翼型优化，上下翼面各布置10个控制点来改变翼型型面，如图1所示。

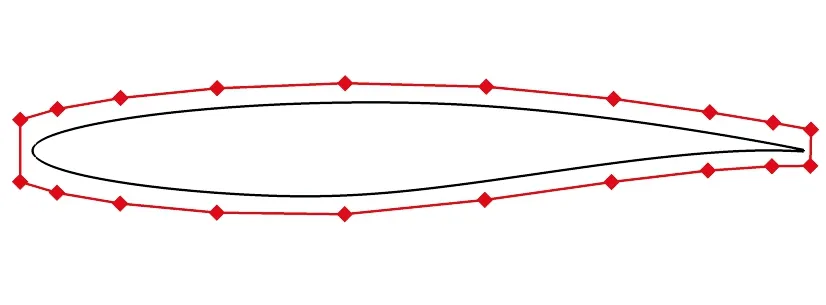
图1 FFD控制框Fig.1 FFD control box

优化网格采用C网格，如图2所示。

图2 翼型优化网格Fig.2 Airfoil optimization mesh

采用基于逆距离权重插值(Inverse Distance Weighting Interpolation，简称IDW)方法[8]来实现空间网格更新，该方法鲁棒性较高。翼型FFD框扰动及网格变形能力如图3(a)所示，可以看出：扰动后的网格仍有较好的正交性；流场计算获得收敛解，压力分布如图3(b)所示。

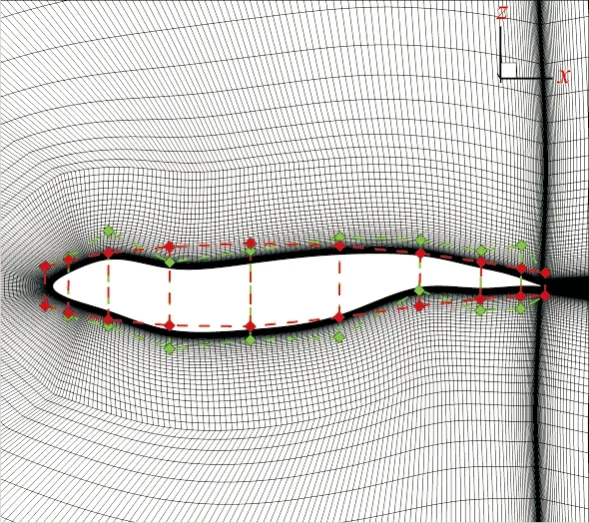
(a) FFD框扰动

(b) 变形后翼型压力云图图3 网格变形Fig.3 Mesh deformation

3 离散伴随方程法

基于梯度的优化算法主要优点是收敛快速，但是其最大的困难是需要高效准确的梯度计算。本文采用基于伴随的梯度优化方法[2]，伴随方程法通过求解原始方程的伴随方程，可以一次求解出目标函数针对所有设计变量的导数。其计算量基本与设计变量个数无关，计算效率极高，并且能够保持很好的精度。

离散伴随方程法直接从已经离散的目标函数及流场控制方程出发，推导出离散形式的伴随方程。如果伴随方程的形式和原始流场控制方程的离散形式完全对应，则可以求解出对应于目标函数和控制方程离散形式的数值精确导数。

在气动外形优化设计中，目标函数一般为阻力系数，构建目标函数表达式为：

FA=f[G(x),Q(x)]

(2)

式中：x为外形设计变量；G(x)为设计变量x确定的CFD计算网格；Q为流场解向量。

流场计算收敛表达式为

RA[Q(x),G(x)]=0

(3)

式中：RA为流场残差。

构建伴随方程，进行伴随算子的求解。

(4)

求解目标函数对设计变量的导数：

(5)

4 优化算法

4.1 梯度优化算法

梯度优化的顶层控制算法采用SNOPT(Sparse Nonlinear Optimizer)算法[9]，能够高效快速处理大规模非线性约束，同时对求解器的调用次数较少。SNOPT的基本思想是：将有约束的非线性优化问题在每一个迭代步上转化为二次规划子问题，在每一步上的二次规划子问题中求解线性化约束条件下的修正拉格朗日函数二次模型的最优化问题。

4.2 全局优化算法

全局优化算法采用并行增广拉格朗日乘子粒子群优化算法[10](Augmented Lagrange Multiplier Particle Swarm Optimization，简称ALPSO)。粒子群优化算法[11-12](Particle Swarm Optimization，简称PSO)是一种模拟鸟群和鱼群社会行为的、基于群体智能的进化算法。PSO最初是由 Eberhart 和 Kennedy 设计研发的。在PSO中，优化问题的求解方案是通过追寻当前的最优值来探索设计空间。粒子通过跟随当前称为导向的最佳粒子在问题空间中探索。

ALPSO方法利用了PSO方法的优点，可解决不光滑目标函数优化问题，更有可能找到全局最优值。ALPSO方法使用增广拉格朗日乘子处理约束，可以被用于解决非线性、不可微、非凸问题。

5 基于梯度优化算法的优化设计框架

本文采用的优化设计框架包括几何参数化模块、动网格模块、流场求解模块、梯度信息求解模块及优化算法模块，如图4所示。首先进行流场求解，优化算法根据目标函数信息和梯度信息产生一组设计变量，更新翼型表面网格及空间网格；然后进行目标函数及目标函数对设计变量梯度的求解；最后将目标函数信息及梯度信息传递给优化算法，优化算法结合优化问题的约束要求，产生下一组设计变量，如此循环直至收敛。

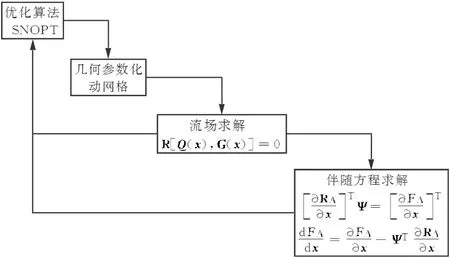
图4 梯度优化算法流程图Fig.4 Gradient-based optimization algorithm flow chart

6 RAE2822翼型的减阻优化

ADODG定义的算例2：基于RANS方程的RAE2822翼型的跨声速减阻优化。关于ADODG case2的研究，国内外已做过很多工作[13]。

自由来流马赫数为0.734，雷诺数为650万，升力系数为0.824(风洞试验采集到的攻角大约为2.79°)，对REA2822翼型进行减阻，优化问题受翼型面积和俯仰力矩的约束。优化问题如下：

min:CD

subject to:CL=0.824

CMy≥-0.092

Area≥Areainitial

其中，CD表示阻力系数；CL表示升力系数；CMy表示俯仰力矩系数；Area表示翼型面积；Areainitial表示翼型初始面积。

优化过程中，为便于优化和直观理解，将面积约束转化为厚度约束，使优化后翼型的厚度不少于翼型的初始厚度，即t≥tinitial，翼型截面共布置了25个厚度约束。翼型优化也布置了前后缘约束，使前后缘控制点变化量大小相等、方向相反。前后缘约束的布置是为了避免因翼型剪切变形导致翼型攻角改变，造成最终的计算攻角不准确。所有几何约束示意图如图5所示。

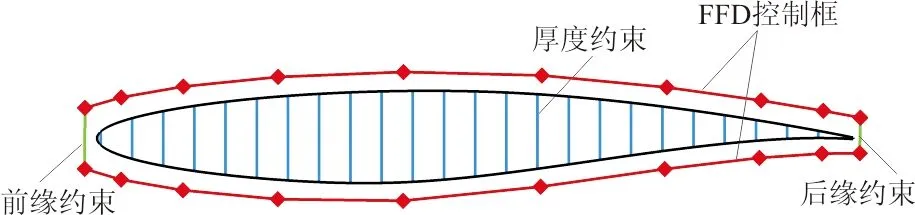
图5 翼型优化几何约束示意图Fig.5 Airfoil optimization geometric constraints

翼型采用FFD参数化方法，上下翼面各10个控制点。设计变量包括FFD控制点及翼型攻角，共计21个。

6.1 初始翼型网格收敛性研究

初始翼型的网格收敛性研究结果如表1所示，阻力系数随网格数的-2/3次幂变化的曲线如图6所示。

随着网格量的增加，阻力系数值逐渐收敛至1 count(1 count=0.000 1)以内，表明所使用的CFD方法及网格具有较好的收敛性。优化采用54 848的网格量。

表1 RAE2822翼型不同网格量计算结果Table 1 RAE2822 airfoil calculation results under different gridsize

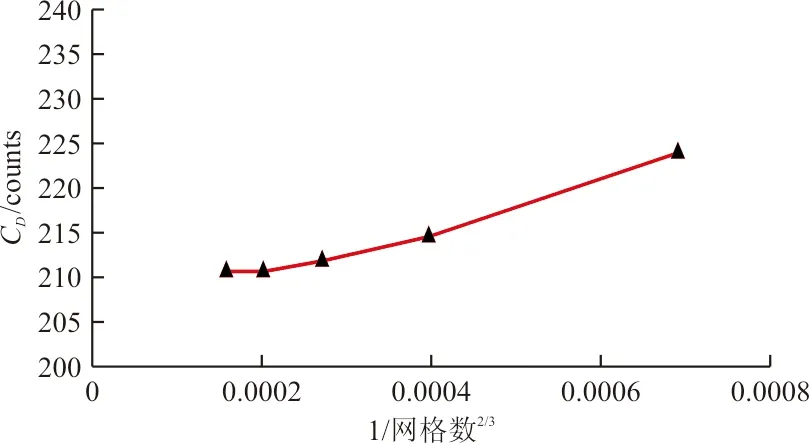
图6 RAE2822翼型网格收敛性研究Fig.6 Grid convergence study for the RAE2822 airfoil

6.2 基于梯度算法的单点优化多极值特性研究

采用拉丁超立方抽样方法对翼型加入初始扰动，翼型控制点的变化范围为(-0.05，0.05)。

生成七组初始扰动变量，初始翼型如图7所示。压力分布对比如图8所示。

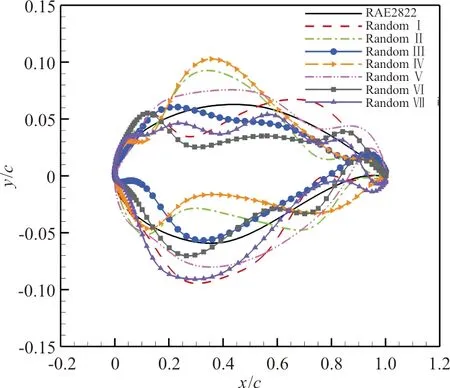
图7 加入不同随机初始扰动后的翼型Fig.7 Airfoil after different random initial disturbances

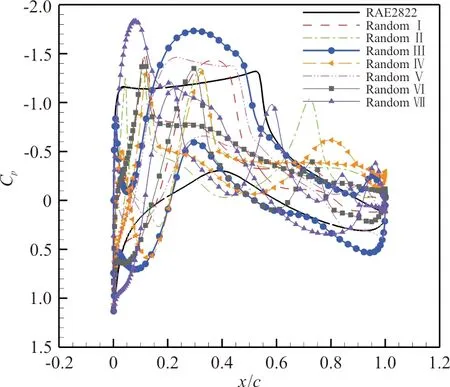
图8 不同随机初始扰动后的翼型压力分布对比Fig.8 Comparison of airfoil pressure distribution after different random initial disturbances

优化后的翼型对比及优化后压力分布对比分别如图9～图10所示。对7个有随机初始扰动的翼型进行相同的优化，从图9～图10可以看出：它们之间只存在细微的差别，阻力系数大小几乎没有差别。

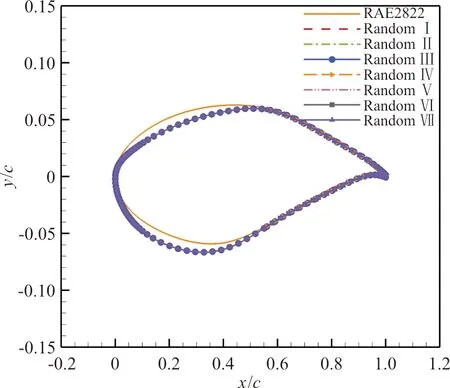
图9 不同初始扰动下优化后翼型对比Fig.9 Comparison of optimized airfoils under different initial disturbance

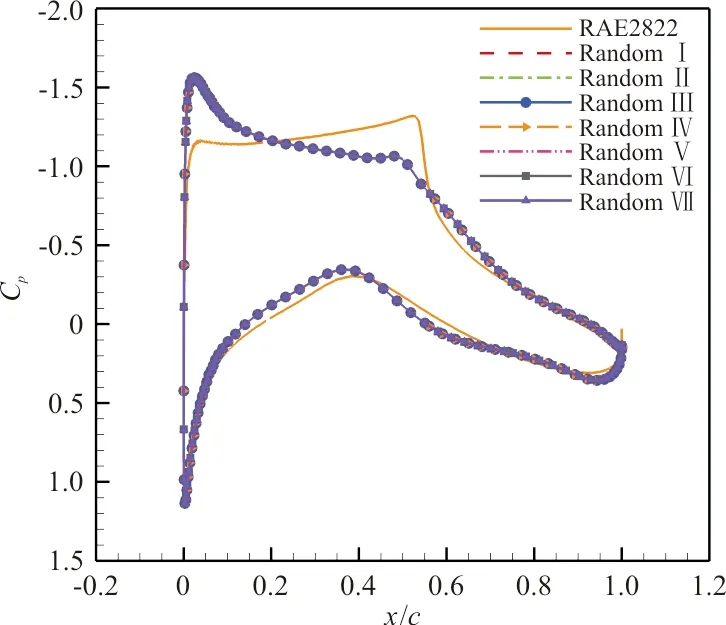
图10 不同初始扰动下优化后压力分布对比Fig.10 Comparison of pressure distribution after optimization under different initial disturbance

梯度优化算法阻力收敛历史和最优度(Optimality)[9,14]收敛历史如图11所示，可以看出：七次随机初始外形优化迭代次数不同，但是结果均收敛，且目标函数值一样。

SNOPT优化算法中最优度(Optimality)的含义是考虑了约束的 KKT 条件数值，用以判断优化是否收敛。不同初始扰动下梯度算法优化结果如表2所示。

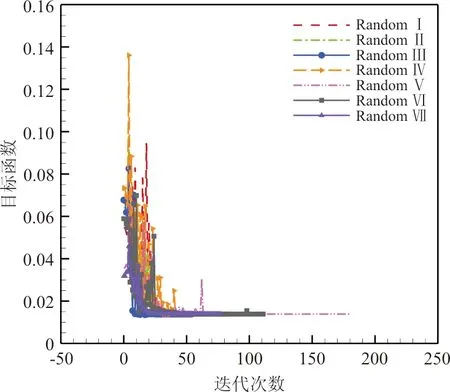
(a) 阻力收敛历史

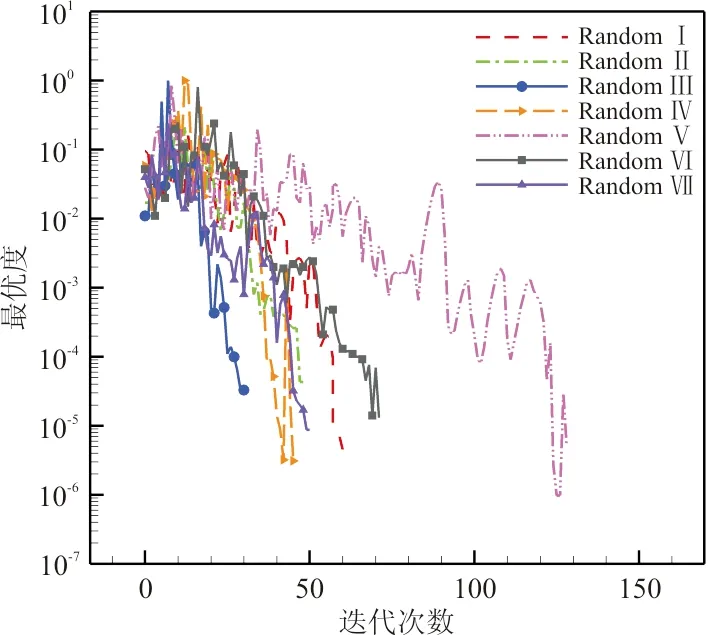
(b) 最优度收敛历史图11 不同初始扰动下梯度优化算法阻力和最优度收敛历史Fig.11 Gradient-based optimization algorithm convergence history and optimality history under different initial disturbance

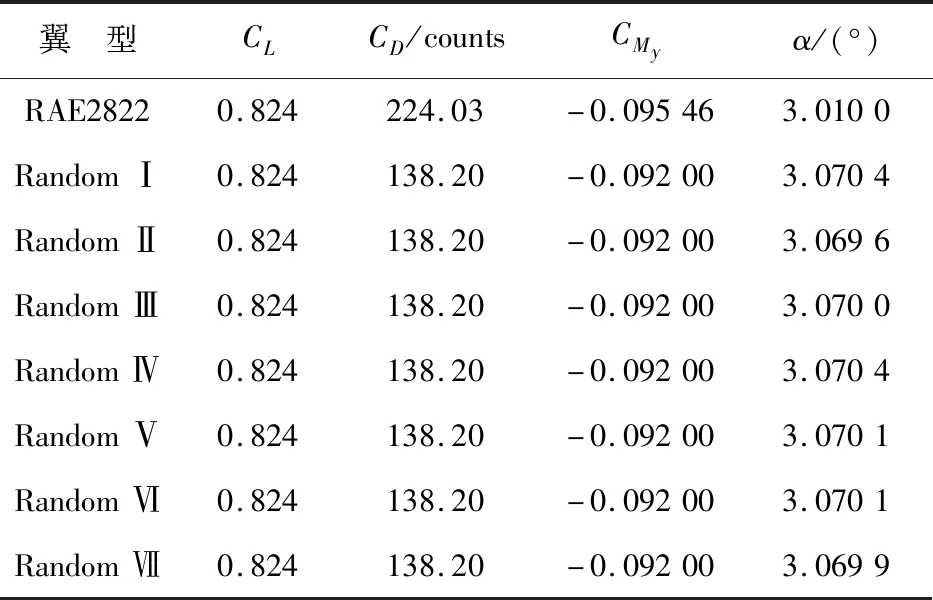
翼 型CLCD/countsCMyα/(°)RAE28220.824224.03-0.095463.0100RandomⅠ0.824138.20-0.092003.0704RandomⅡ0.824138.20-0.092003.0696RandomⅢ0.824138.20-0.092003.0700RandomⅣ0.824138.20-0.092003.0704RandomⅤ0.824138.20-0.092003.0701RandomⅥ0.824138.20-0.092003.0701RandomⅦ0.824138.20-0.092003.0699

为了更好地使设计空间可视化，任选三个优化结果，计算该三个优化设计点的设计变量的欧氏距离，如图12所示。

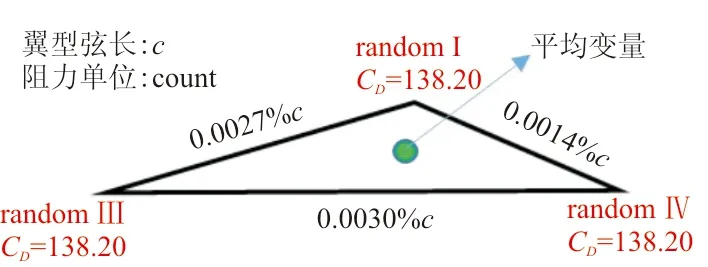
图12 多个局部极小值之间的欧氏距离Fig.12 Euclidean distance between multiple local minimums

当前设计空间的最大欧氏距离为0.45c，这三个优化设计点的设计变量之间的距离很短，最小欧氏距离为0.001 4 %c，最大为0.003 0 %c，而优化出的设计点的变量间的欧氏距离远远小于0.45c。基于计算数据，可以得出此气动外形优化问题的设计空间是凸状的。

为了验证此气动外形优化问题的设计空间可能是单峰值的，又选取以上三个优化点的设计变量的平均值，如图12中圆点所示，其气动力计算结果如表3所示。

表3 平均变量翼型的气动力Table 3 Aerodynamics of mean variables airfoil

从表3可以看出：阻力已大幅减小，其数值与Random Ⅰ，Random Ⅱ，Random Ⅲ优化后的阻力数值一样，并没有发生突变，验证了此优化空间很可能是单峰值的。

这次优化也表明气动优化方法的鲁棒性以及梯度伴随方法的优越性。即使给翼型任意的初始扰动，也能优化出效果较好的翼型，设计点阻力大幅减小。

6.3 优化翼型网格收敛性研究

对Random Ⅰ的优化翼型进行网格收敛性研究，优化翼型的网格收敛性研究结果如表4所示，阻力系数随网格数的-2/3次幂变化的曲线如图13所示，可以看出：随着网格量的增加，阻力系数值逐渐收敛至1 count以内。

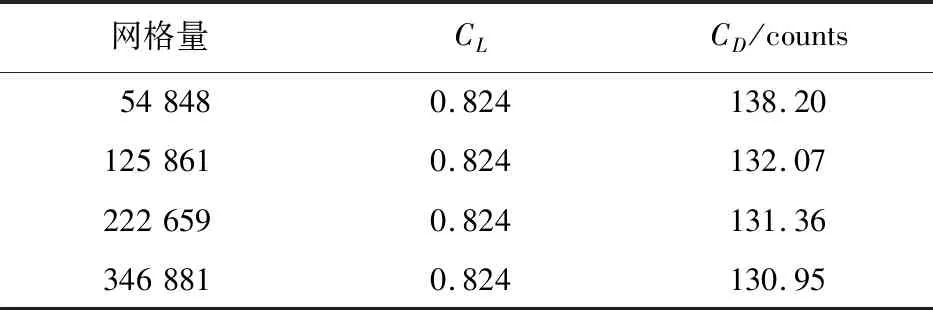
表4 优化翼型不同网格量计算结果Table 4 Optimization airfoil calculation results under different gridsize

图13 优化翼型网格收敛性研究Fig.13 Grid convergence study for the optimization airfoil

6.4 设计变量个数对优化设计结果的影响

进一步探究设计变量维数的变化对优化结果的影响，上下翼面各布置10、18和25个设计变量，梯度算法优化结果如表5和图14所示。

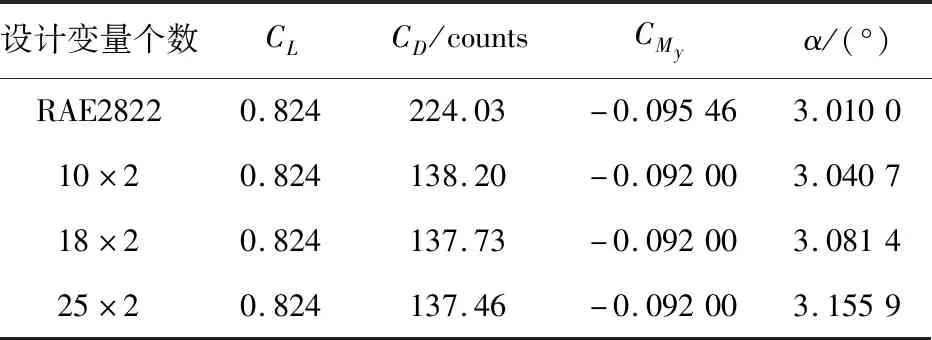
表5 不同设计变量个数梯度算法优化结果Table 5 Gradient-based algorithm optimization results under different number of design variable

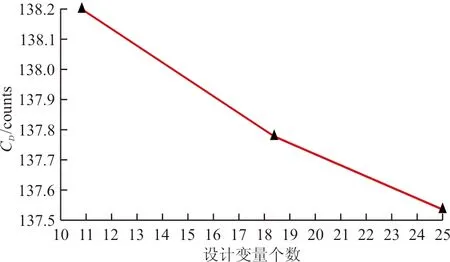
图14 不同设计变量的优化结果Fig.14 Optimization result with different number of design variables

从表5和图14可以看出：随着设计变量的增多，减阻效果更好，但是采用10×2个设计变量和采用25×2个设计变量的梯度优化结果阻力系数差别在1 count以内。

优化后的翼型对比及优化后压力分布对比如图15～图16所示，可以看出：优化结果基本一样。

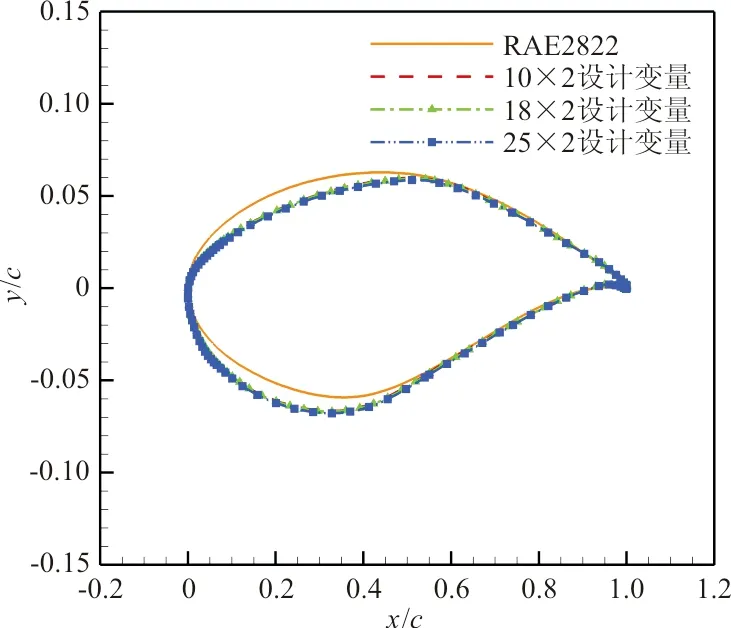
图15 不同设计变量个数优化后翼型对比Fig.15 Comparison of optimized airfoils with different number of design variables

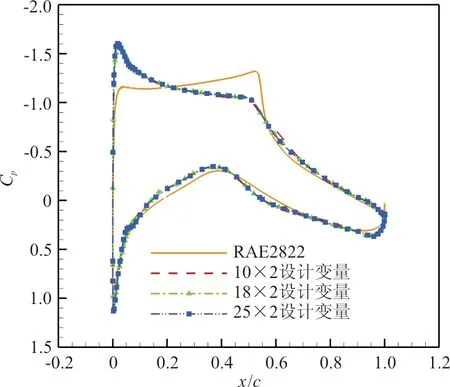
图16 不同设计变量个数优化后压力分布对比Fig.16 Comparison of pressure distribution after optimization with different number of design variables

不同设计变量个数梯度优化算法阻力收敛历史和最优度(Optimality)收敛历史如图17所示，可以看出：设计变量增多会导致优化迭代次数增加，但是结果均收敛，且目标函数值相差不大。

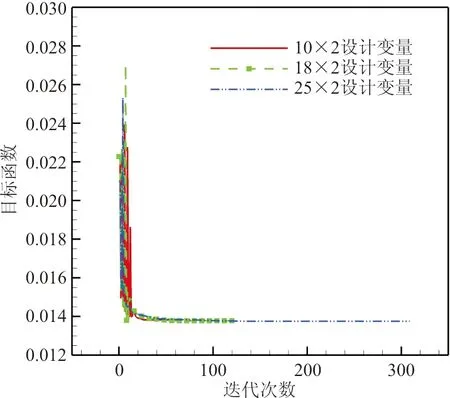
(a) 阻力收敛历史

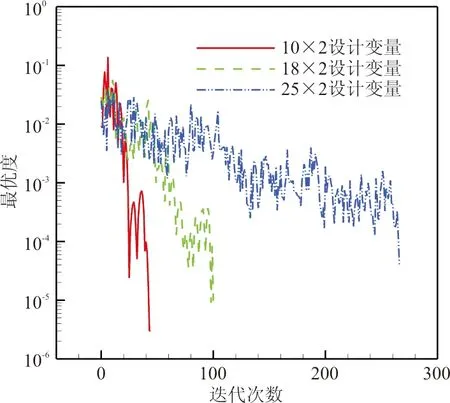
(b) 最优度收敛历史图17 不同设计变量个数梯度优化算法阻力和最优度收敛历史Fig.17 Gradient-based optimization algorithm convergence history and optimality history under different number of design variable

6.5 全局算法和梯度算法优化结果对比

采用全局优化算法中的粒子群算法求解上述优化问题，在使用相同核数的情况下(8核)，全局算法耗时约两周，而梯度优化算法仅耗时约5小时即可获得相对满意的结果。

全局算法和梯度算法优化结果对比分别如表6、图18～图19所示。

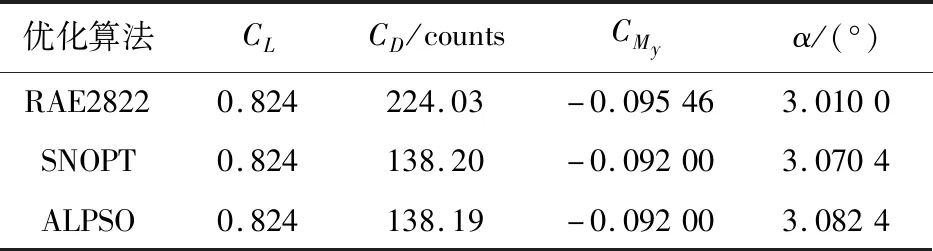
表6 不同优化算法优化结果Table 6 The results of different optimization algorithms

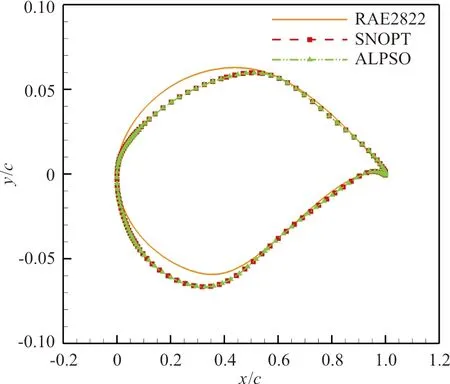
图18 不同优化算法优化前后翼型对比Fig.18 Initial and optimized airfoil comparison using different optimization algorithms

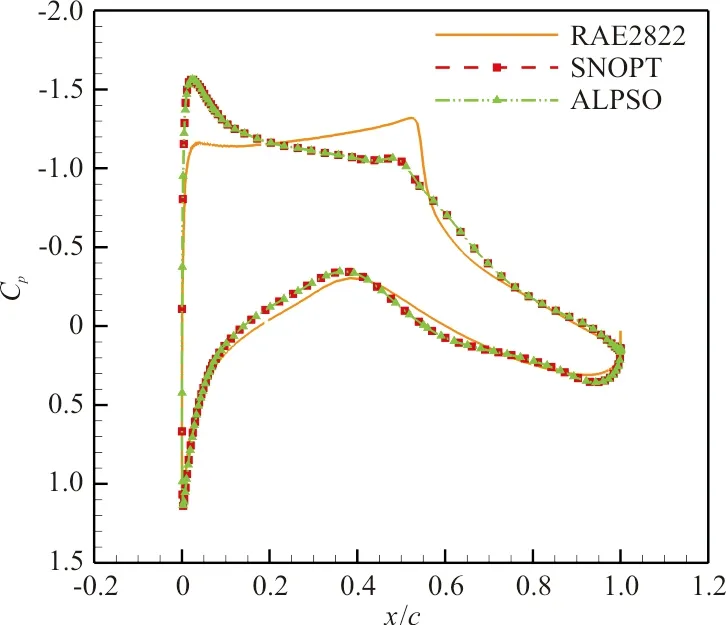
图19 不同优化算法优化前后压力分布对比Fig.19 Initial and optimized pressure distribution using different optimization algorithms

从表6可以看出：粒子群优化算法阻力减小85.84 counts，梯度优化算法阻力减小了85.83 counts，优化结果基本一样。

从图18～图19可以看出：翼型与压力分布优化结果也一致。但是基于伴随的梯度优化方法计算时间短，效率更高，更适用于实际气动外形优化时有大规模设计变量的问题。

7 结 论

(1) 在满足设计约束的前提下，分别采用全局、梯度优化设计平台对初始翼型进行单目标优化，改善翼型的性能。全局优化算法耗时久，优化效果最好；但梯度优化算法优化效率极高，最终的优化结果也有很好的收益。全局优化算法更适用于设计变量离散、目标函数不连续以及有多个局部最优解的设计问题，但是在大规模设计变量问题中，其计算代价是不可接受的。

(2) RAE2822翼型减阻设计的设计空间很可能是单极值的，但该结论还需要进一步证明。

(3) ADODG的case2可能是一个单峰值气动设计问题，但是对于涉及大规模几何设计变量的气动外形优化问题或者非常规布局的优化设计问题，可能是多峰值的，其峰值数量可能与几何变形的能力有关，仍需进一步探索。

(4) 设计变量增多对优化结果有一定的改善作用，但是设计变量增多会导致优化迭代次数增加，ADODG的case2中10×2个设计变量已能够得到好的优化结果。