基于二进制粒子群算法的战时航空网络规划研究
2019-11-04叶泽龙吴明功朱德山温祥西
叶泽龙,吴明功,朱德山,温祥西
(1.空军工程大学 空管领航学院,西安 710051) (2.空军工程大学 国家空管防相撞技术重点实验室,西安 710051) (3.中国人民解放军 93220部队,哈尔滨 150046)
0 引 言
在战时,空域用户多,各类航空器活动频率高,空域环境复杂多变,为军航活动提供更为有利的保障,关乎战事走向和国家安全;同时,经济因素也是影响战争潜力的重要因素,战时民航运输关系到国计民生。在优先保障军航的前提下,兼顾民航效益,尽可能避免航空资源的浪费,做好战时航空管制工作,很有必要。战时航空管制,是指在战争期间,航空管制机构通过组织和协调我方航空器的飞行活动,以及对作战空域的连续监视和控制,从而保障我方对空域使用的安全性、有序性和灵活性,提高作战效能的一种战场调控活动[1]。
国内外已围绕战时航空管制问题展开了大量研究。1973年,美国建立了全国空军战区空域管制条令,是世界上第一个发布战时航空管制条令的国家[2];1995年,美军参谋长联席会议颁发了第JP 3-56号联合出版物《联合空中作战指挥与控制》[3];2000年和2003年相继发布了《一体化空战场管制程序》和《联合空中交通管制程序》,标志着战时航空管制理论成体系化发展,渐趋成熟。2014年,美军颁布了JP 3-52号联合出版物《联合空域管制》,使其战时航空管制发展更加趋于完善。在系统建设上,研发了JASMAD等系统,用于排解战斗空间内的飞行冲突,提供动态管理能力[4-5]。在军事实践方面,在伊拉克战争、“奥赛德黎明”等军事行动中,美军的战时航空管制理论、法规条令、系统,经受住了战争检验,帮助美军牢牢掌握了战区内的空域管制权,使得指挥控制顺畅自如[6]。国内关于战时航空管制问题的研究,主要是从法理角度进行探索,例如,刘宝新等[7]分析了民航租赁飞机战时国防动员的法理依据并提出了动员风险规避对策。也有相关文献应用航空网络对中国民航网络进行定量分析[8-9],例如闫玲玲等[10]、隋东等[11]分析了航空网络抗毁性在不同攻击策略下的变化情况;张豫翔等[12]分析了一定修复成本约束下的航空网络的修复问题。但这些研究主要是针对民航网络损伤后的修复问题,没有从服务作战的角度对战时航空网络进行宏观规划。
上述研究主要是从法理角度,规范战时空中秩序,以定性分析为主,主要成果也都是相关法令法规,定量分析还比较少。本文借鉴航空网络理论,提出一种基于二进制粒子群算法(BPSO)的战时航空网络规划策略,从宏观上对战时航空活动进行规划,在保障军事行动的同时,兼顾民航效益。
1 航空网络规划问题描述
机场是一种重要的航空资源,在经济上可以带动区域经济,吸纳和集聚生产力的各种能量和要素,在战时也有重要的军事作用,例如可以用于保障军航飞机起降,缓解作战飞机的保障压力。在战时,临时征用部分民航机场必将导致民航网络整体性能的下降。民航网络性能下降的幅度取决于战争的规模。在局部作战中,军航活动需要使用的航空资源较少,民航网络性能需要下降的幅度较小;若进入全面战争状态,民航资源可能会被大量征用,民航网络性能则会大幅下降。据此,本文用民航网络性能维持在怎样的程度PE(百分比)作为征用民航机场的一个限制条件,PE大小与战争规模成反比。战时航空网络规划还要考虑战场环境和作战意图,例如战争爆发在哪一区域、战争要达到怎样的目的等。基于此,可以生成禁止征用/必须征用的机场清单,禁止征用清单内的机场,通常承担交通枢纽等作用,在战时不可征用;必须征用清单内的机场,通常在战事中起到重要的军事意义。综上,其规划流程如图1所示。
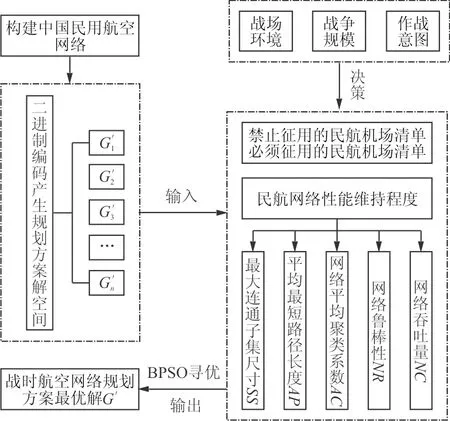
图1 战时航空网络规划流程Fig.1 Air network planning process in wartime
1.1 航空网络模型建立
航空网络是以民航机场为节点,以机场之间的航班为连边构成的网络,是一种典型的复杂网络,其结构可表示为G={V,E,W}。其中,V={v1,v2,…,vn},代表航空网络中节点的集合,本文选取民航机场作为节点;E={e1,e2,…,el},是网络中连边的集合,若机场之间有固定航班,则认为两点之间有连边;W={w1,w2,…,wm},代表航空网络中的边权,本文选取各航线上一定周期内的航班数量为航空网络赋权[13]。
为了简化模型,做出如下假设:
①航空网络中,两个节点间采取双向航空运输,不同方向的运输除了存在飞行高度层等差异,其路径基本一致、往来流量接近对等,因此将其视为无向网络;
②同一城市若存在多个民航机场,予以合并,以城市名称命名(例如上海虹桥机场与浦东机场合并为上海机场);
③经停航线拆分为多段直飞航线,例如长春-太原-西安航线,拆分为长春-太原、太原-西安两段航线;
④战时不开辟新的航线,也不增加新的机场。
本文选取国内199个民航机场及其航班数据构建中国航空网络模型,数据来源于http:∥www.qunar.com。对199个机场之间一月内航班数进行统计,部分数据如下:

此邻接矩阵反映了成都、深圳、昆明、西安、重庆、杭州等六个城市之间的航行情况。
1.2 航空网络性能测度指标
航空网络性能的评估是战时航空网络规划的重要工作,准确评估网络性能是合理规划战时航空网络的关键。网络性能一般可以从网络总体运输能力、连通性能、抗毁性、运行效率以及网络结构是否健康等五个方面进行评估。据此提出以下五个测度指标。
(1) 最大连通子图尺寸SS。在网络中,连通性的判据一般为任意两点之间是否存在通路。若网络中所有节点之间都是连通的,则称该网络为完全连通;当网络为不完全连通时,该网络便可划分成若干个连通的子图,称其为连通子图[14]。连通子图中节点的个数称为规模,规模最大的连通子图即为最大连通子图。SS越大,网络连通性越好[15]。
(2) 网络平均最短路径AP。其定义为网络中任意两点之间最短路径之和占网络中可能存在的最多边数的比重:
(1)
AP可以描述网络的脆弱性和抗毁能力。在复杂网络中,AP越小,说明任意两个节点之间的传输越快,连通性越好,风险值也越小[16]。在航线网络中,AP越小,意味着航空器在机场节点之间运输所需的中转次数越少,中转成本越低,业务往来更加迅捷。例如,一个航线网络的AP=2.453 1,表示从该网络中任意一个机场出发,到达另一个机场,平均需要中转1.453 1次。
(3) 网络平均聚类系数AC。点的集群系数是用来描述节点之间聚集成团程度的系数。加权集群系数[17]的计算公式为
(2)
式中:si为节点权;ki为度值;节点j、k为节点i的两个相邻节点;aij为节点的连接状态,当节点i、j互连,aij=1,否则aij=0。
(3)
AC表示整个网络的聚集程度。
(4) 网络鲁棒性NR。网络鲁棒性反映了网络点权分布的均匀程度。
(4)
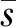
网络的NR越大,流量分布越均匀,其鲁棒性能也就越好,可作为航空网络运输能力的度量。
(5) 网络吞吐量NC。NC表示所有航线上一段时间内的航班量总数,可作为网络运输能力的一个度量。
(5)
2 基于AHP的航空网络性能评估
为了评估民航网络的整体性能,需要综合各个指标进行评判。本文选择层次分析法(AHP)对各指标的权重进行计算。AHP是一种将与决策相关元素分解成多个层次,以此为基础进行定性和定量分析的决策方法[18]。应用1-9标度表对五个指标的重要程度进行排序。aij为因素i与因素j比较后产生的结果,用1-9标度法可以反映因素i与因素j相比的重要程度。标度及说明如表1所示。

表1 标度及说明Table 1 Scale and explanation
应用AHP方法处理前,应对各指标进行归一化处理,计算{G′}中各指标的最值,如表2所示。

表2 各指标最值Table 2 The maximum value of each index
比较本文选取的航空网络的五项指标。NC反映民航的航班规模,最为直接地反映经济效益,在五个指标中最为重要;SS描述网络中相互可达机场的规模,既可反映网络的连通性,也可反映网络的稳健性[19],认为其重要性仅次于NC;AP可以反映网络损坏后,选取备份航线的成本高低,AP越短的航空网络在部分航线损坏后通过其他机场中转带来的成本相对较小,认为AP是第三重要的;AC通常用于判断集团化水平,认为其重要度与AP大致相当;NR反映网络中流量分布的均匀程度和网络的鲁棒性,被认为是最次要的指标。综上,五个指标的重要度排序为NC>SS>AP=AC>NR。前两个指标分别反映网络的运输能力和互通机场规模,后三个指标则衡量网络的抗毁性和健康程度。矩阵A描述了NC、SS、AP、AC、NR五个指标之间的比较结果。

(6)
计算矩阵A的最大特征根,及其相应的特征向量,并进行归一化处理,得到权重向量W:
(7)
W=[W1W2W3W4W5]
=[0.501 0 0.246 1 0.103 8 0.103 8 0.045 3]
而后进行一致性检验,计算最大特征值λmax:
一致性指标CI为
一致性比重CR为
其中,RI为随机一致性指标,当n=5时,RI取1.12。CR<1,因此判断矩阵满足一致性检验,各指标权重为:WNC=0.501 0,WSS=0.264 1,WAP=0.103 8,WAC=0.103 8,WNR=0.045 3。
由于各数据数量级的差异,对指标进行归一化处理,得到归一化处理后的指标NCi,SSi,APi,ACi,NRi。
综上所述,5个复杂指标的加权和,即综合重要度值Wi:
Wi=0.501 0×NCi+0.246 1×SSi+0.103 8×
APi+0.103 8×ACi+0.045 3×NRi
(8)
根据式(8)及指标归一化后的结果,计算原网络G(含199个机场)的初始网络性能WG=0.833 5。
在此基础上,进行战时航空网络规划:首先结合战争规模,判断民航网络应当维持在某种程度(PE),而后结合作战意图、战场环境等因素生成禁止征用/必须征用机场清单,以使用尽可能少的民航机场维持预期网络性能为优化目标,最终通过BPSO算法求解。具体为
minn′
(9)
s.t. [0.501 0×NCG+0.246 1×SSG+0.103 8×
APG+0.103 8×ACG+0.045 3×NRG]≥
WG×PE
(10)
s.t.i,j……k∈N′
(11)
s.t.p,q,……l∉N′
(12)
N′∈N
(13)
式中:N={1,2,…,n},为原网络G中民航机场的编号;N′为规划后网络G′中机场的编号;n′为机场数目。
式(9)为优化目标,即民航机场数目;式(10)为约束条件,即G′的网络性能必须维持在期望程度以上,NCN′,SSN′,APN′,ACN′以及NRN′分别为G′的测度指标,PE为百分比;式(11)为必须征用的机场清单;式(12)为禁止征用的机场清单。
3 基于BPSO的战时航空网络规划
采用若干199维的0、1值构成的二进制串描述随机组合的战时航空网络规划方案。为“0”的位置表示机场不在方案内;为“1”的位置对应此机场在规划方案中,其编码方式如图2所示。

图2 编码示意图Fig.2 Schematic diagram of coding
本文是一个典型的0-1规划问题,使用BPSO算法可以准确快速地对此问题进行求解。
3.1 BPSO基本原理
BPSO算法是一种由PSO算法发展而来的可以快速寻优的算法,且位置和速度更新均为离散值[20]。本文提出的战时航空网络规划方案在描述上是离散形式的,使用BPSO算法可以在随机产生的大量规划方案集合中快速寻出符合条件的规划方案。
PSO算法的粒子初始位置、更新速度都是连续函数[21-22],与之相对应,BPSO均为离散形式,其速度更新公式为
Vid=ω·vid+c1·rand()·(pid-xid)+
c2·rand()·(pid-xid)
(14)
式中:ω为权重,通过改变ω可以调整粒子的搜索速度;c1、c2为学习因子,分别调节局部最好粒子和全局最好粒子的更新。
式(13)产生速度,速度的值是为了描述二进制串的位置xid变为“1”值的概率,Vid∈[V-max,Vmax]。为了将速度映射到[0,1]之内,还须采用sigmoid函数:
(15)
式中:s(vid)为粒子中某位xid取“1”的概率。
(16)
粒子通过公式(15)改变xid位置上的“0”、“1”位值。Vmax用于限制Vid的范围,防止s(vid)过于接近“0”或“1”。通过sigmoid函数,保证粒子的位置不是“0”即为“1”。
3.2 算法步骤
算法的步骤如图3所示,具体如下:
Step1:初始化。随机产生一组粒子,维度为199,用其“0”、“1”编码情况描述战时航空网络规划方案,根据禁止征用清单/必须征用清单对粒子的特殊位置置“0”或“1”。
Step2:计算每个粒子的适应度(方案G′中机场数目),根据编码信息计算G′的网络性能WG′,并判断其是否符合约束条件。
Step3:更新粒子的位置速度。
Step4:将各方案的机场数目与当前符合约束条件的最小机场数目进行比较,更新群的最优方案。
Step5:判断迭代次数是否满足条件。若不满足返回Step2。若满足,输出最优方案及对应网络性能的值。

图3 算法步骤Fig.3 Algorithm steps
4 仿真分析

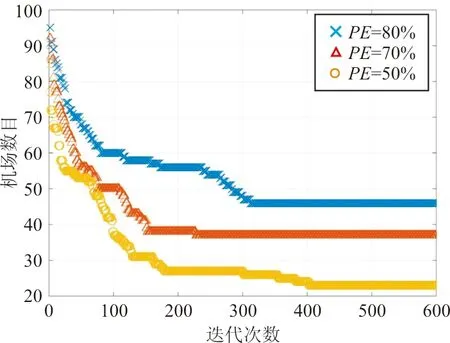
图4 不同PE下收敛曲线图Fig.4 Convergence curves under different PE
一份中国民航机场的重要度排名如表4所示,该排名与机场总容量排名并不完全一致,但该排名前五十的机场其月航班数基本在1 000次以上,排名前十的月航班数更是基本超过10 000次,据此定义该排名中重要度前五十的为较重要机场、前十位的为重要机场。

表3 不同PE下的战时航空网络规划方案Table 3 Wartime aviation network planning under different PE
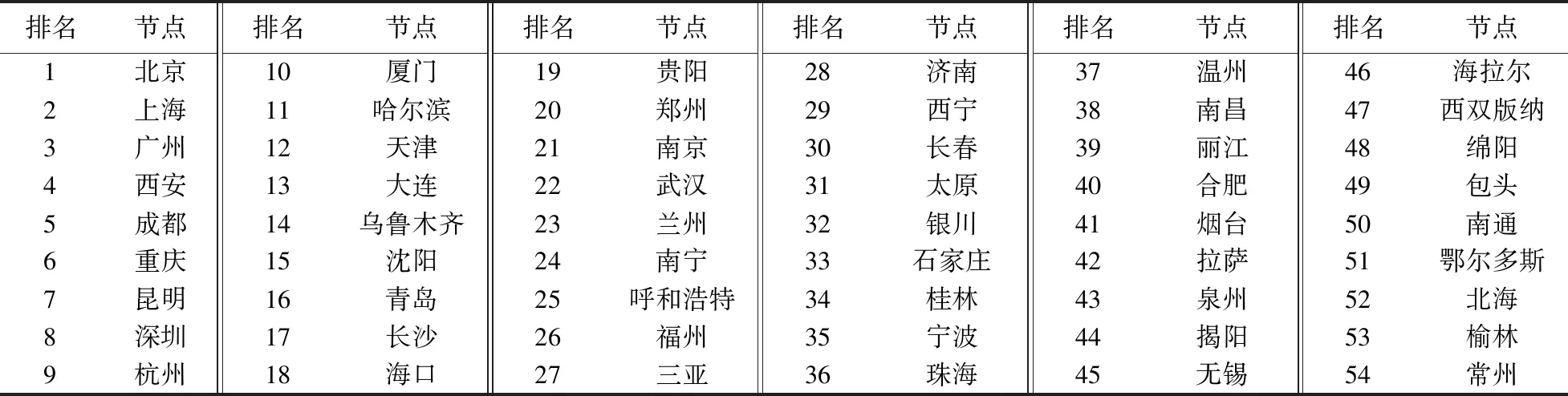
表4 民航机场重要度排名Table 4 Civil aviation airport importance ranking


表5 指定作战条件下PE=80%的规划方案Table 5 Planning scheme of PE=80% under given operational conditions
图5 给定作战条件下PE=80%收敛曲线图Fig.5 The convergent curve of PE=80% under given operational conditions
对比考虑作战条件和不考虑作战条件时PE=80%的规划方案,二者在不同约束条件下,规划出了两种战时航空网络。对比两种战时航空网络,可以发现重要度高的机场,除去被强制征用的,其余均仍为战时航空网络的主干,而在对重要度降低的机场的选择上,差异较大,这与航空网络性能评价指标体系以及航空网络的拓扑结构有关。这表明,在本方法中,对高重要度的机场征用应当较为慎重,这些起到骨干作用的机场的变化,将对其他机场的选取和战时航空网络结构产生重要影响。
从防御角度上,可以得到一点启示:战时,高重要度机场在大多数情况下,都应当做重点防御;而对其他机场的防御,不是一成不变的,应当结合实际,因时制宜。考虑作战条件后,最少机场个数增加了11个,表明规划结果受作战意图及战场环境的影响较大;另一方面,也反映出战时航空网络规划问题具有较强的主观能动性,更好的掌握战场环境、掌握上级意图,可以提高规划的科学性,降低对航空资源的浪费。
5 结 论
(1) 本文所提战时航空网络规划方法,能够结合作战意图、战场环境,应用航空网络思维调配战时航空资源,该方法可以为战时航空管制工作提供理论参考。
(2) 二进制粒子群算法适用于战时对机场这一航空资源的分配。
今后将在此研究的基础上,探索更精确的战时航空网络规划方法以及更高效的求解算法,进一步探索航路等航空资源的分配问题。
