开链式多连杆机构的逆运动学求解算法

康凯 刘婷婷 王二建 李红艳 朱国权 周建新

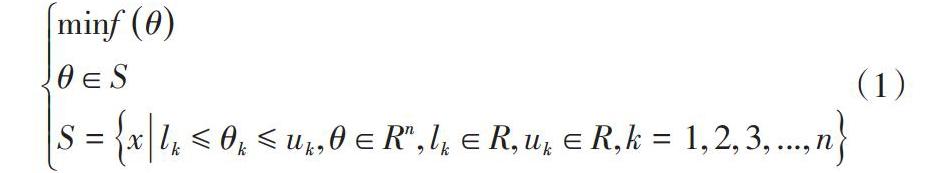
摘要：在D-H坐标系下，建立普适的开链式多连杆机构的正运动学模型较易，但建立通用的逆运动学模型却相当困难，并且其复杂程度随着关节个数的增多而显著增大。为此，结合粒子群优化算法（PSO），通过迭代的方式求解逆运动学问题。针对PSO算法求解时的精度不高、易陷入局部极值的缺点，提出局部搜索策略，提高解的精度，并采用逃逸策略保证种群多样性，使算法在全局中搜索。经验证，改进后的PSO算法是一种精确、有效的求解逆运动学的算法。

关键词：逆运动学;粒子群优化算法;局部搜索;逃逸策略

中图分类号：G242        文献标识码：A

文章编号：1009-3044（2019）23-0209-04

开放科学（资源服务）标识码（OSID）：

1 引言

开链式多连杆机构的逆运动学是指在给定末端操作器位姿的条件下求解各个关节变量的取值。逆运动学作为机器人轨迹规划和轨迹控制的基础，是机器人学的关键部分。求解逆运动学问题常采用封闭解法，其特点是编程实现简单，计算速度快，物理意义明确，并且可以找到所有可能的解[1]。但其在很大程度上受到机械结构的限制，需要针对不同类型结构建立不同的模型。

粒子群优化（Particle Swarm Optimization， PSO）是一种模拟鸟类觅食行为的全局优化算法，由Kennedy和Eberhart于1995年提出[2]。基于PSO算法的逆运动学求解，意在关节变量空间中搜索出最优解。搜索过程仅依赖于正运动学，而正运动学的计算是不受机构的结构限制。因此，PSO算法在求解逆运动学问题上体现出较高的普适性[3]。

但是，PSO算法的结果不能达到理想的精度，需对每一代的最优解增添一项局部搜索。此外，PSO算法对多峰值复杂函数搜索的效果不佳，易陷入局部最优[4]。可引入逃逸策略后，增强了种群的多样性，及时地跳出局部最优。

2 问题描述

逆运动学问题的求解可转化成式（1）的方式进行描述：

[minfθθ∈SS=xlk≤θk≤uk，θ∈Rn，lk∈R，uk∈R，k=1，2，3，...，n] （1）

其中[S]是[n]维空间中的一个非空集合，[n]代表关节变量的个数。函数[fθ]是定义在[S]上的目标函数。

如图1所示，在笛卡尔坐标系中，末端操作器位姿矩阵[W]表示为：

[W=NxOxAxPxNyOyAyPyNzOzAzPz0001=NOAP0001]            （2）

其中，[NOA]表示姿态，[P]表示位置，目标位姿矩阵设为[W?]，则位置误差为：

[εP=Pθ-P?Pθ-P?T]                   （3）

姿态误差为：

[εN=NθN?+OθO?+AθA?-12]              （4）

目标函数写成：

[fθ=εP+εN]                          （5）

[Pθ]、[Nθ]、[Oθ]、[Aθ]由正运动学方程求得。

3 逆运动学求解

3.1 基本粒子群算法

PSO算法源于对鸟群觅食行为的模拟，鸟群中的个体通过共享信息保持鸟群飞行的一致性。个体间的信息共享机制确保群体的运动产生从无序到有序的演变，这是PSO算法的基础[4]。

在PSO算法中，每个粒子代表鸟群中的个体，其包含位置和速度两种信息。每个粒子的位置代表着优化问题的一个解。粒子位置坐标对应目标函数的值作为该粒子的适应度，其决定粒子性能的优劣。每个粒子的速度控制其飞行的方向和距离。在每次迭代中，粒子将当前位置与自身发现的最好位置（[pbest]）和所有粒子发现的最好位置（[gbest]）做比较，更新自身的位置和速度[5]。

在逆运动學问题中，设搜索空间[S]是[N]维，粒子的群体规模为[M]，第[i]（[i=1，2，...，M]）个粒子的位置为[θi=θi1，θi2，...，θiN]，其经历最好的位置为[pbesti=pbesti1，pbesti2，...，pbestiN]，速度为[vi=vi1，vi2，...，viN]，所有粒子发现的最好位置记为[gbest=gbest1，gbest2，...，gbestN]。

PSO算法的进化方程为：

[vijt+1=wvijt+c1r1pbestij-θijt+c2r2gbestj-θijtθijt+1=θijt+vijt+1]    （6）

其中，[i=1，2，...，M][j=1，2，...，N]，[t]表示迭代次数，[w]为惯性权重决定继承当前速度的能力，[c1]、[c2]为学习因子决定粒子自我总结和向优良个体学习的能力，[r1]、[r2]为[0，1]之间均匀分布的随机数。

基本粒子群的算法步骤如下：

①随机初始各粒子的位置和速度。

②计算各粒子的适应度，将粒子[i]的位置存入[pbesti]中，将[pbest]的最好位置存储在[gbest]中。

③采用（6）式更新粒子的位置和速度。

④计算各粒子的适应度，若当前粒子[i]的适应度优于[pbesti]，更新[pbesti]。

⑤将[pbest]的最好位置存储在[gbest]中。

⑥若[gbest]满足精度要求或达到最大迭代次数，算法结束，否则，返回③。

实际在更新粒子的位置时，还应考虑是否越界的问题，即[θj]是否超出了第[j]维坐标的范围。若超出范围，则将边界值赋给[θj]。

3.2 改进的粒子群算法

3.2.1 局部搜索

受惯性权重、学习因子等参数的影响粒子移动步长具有随机性。因而，即便某个粒子进入最优解的势力范围内，也未必能够精确地落在最优解的位置，进而影响到最优解的精度。局部搜索用来改善当前粒子的位置，即搜索粒子邻域内的更优解。若存在更优的位置，则用更优的位置代替当前的位置。

局部搜索的对象可以是整个种群，也可以只对当前最优粒子进行局部搜索。在相同的种群规模和迭代次数的条件下，前者求解精度更高，而后者计算量小一些。考虑算法对时间的要求，本文采用后者的方式。

若在粒子邻域内盲目的搜索，势必会影响算法的效率。沿着负梯度方向进行搜索可以快速找到粒子邻域内极值点，确保了算法的效率[6]。

下面讨论目标函数梯度的求解，在D-H坐标中[7]，末端操作器的位姿矩阵由变换矩阵[Ai]连乘得到如式（8）所示，变换矩阵[Ai]表示成如下的形式：

[Ai=cosθi-sinθicosαisinθisinαiaicosθisinθicosθicosαi-cosθisinαiaisinθi0sinαicosαidi0001]（7）

[Wθ=A1A2...An]                      （8）

在矩阵[Ai]中，[ai]、[αi]、[θi]、[di]分别是关节偏移、关节扭转、旋转关节的关节变量、滑动关节的关节变量，对于具体的机器人来说，[ai]、[αi]是固定不变的。

现只考虑关节变量是旋转变量的情形，矩阵[Ai]对[θi]求偏导，得：

[?Ai?θi=-sinθi-cosθicosαicosθisinαi-aisinθicosθi-sinθicosαisinθisinαiaicosθi00000000]

[=0-100100000000000Ai=RiAi]                             （9）

由式（9）可以推出末端操作器的位姿矩阵[Wθ]对[θi]的偏导数：

[?Wθ?θi=?Nθ?θi?Oθ?θi?Aθ?θi?Pθ?θi0000=A1A2..RiAi.An] （10）

因而推出[fθ]对[θi]的偏导数：

[?fθ?θi=2Pθ-P??Pθ?θi+2NθN?+OθO?+AθA?-1?Nθ?θiN?+?Oθ?θiO?+?Aθ?θiA?]（11）

用[?fθ]表示[fθ]的梯度，由式（11）得：

[?fθ=?fθ?θ1?fθ?θ2...?fθ?θN]           （12）

在沿着负梯度方向进行搜索时，还应考虑搜索步长[λ]。若搜索步长设置的过长，虽然搜索速度快，但算法易發散。若搜索步长设置过短，虽然搜索速度慢，但算法收敛性能好。既然是局部搜索，考虑到粒子本身已经接近最优值，因而采取小步长的方式进行搜索是最佳的[8]。

若将关节变量[θ]采用二维向量的方式进行表示，沿着负梯度方向上的搜索如图2所示，图中的同一曲线上的点具有相同的适应度。每步搜索可写成式（13）的形式。

[θ=θ-λ?fθ]                     （13）

设最大搜索步数为[MS]，在一代中粒子[i]的适应度最优，对粒子[i]做局部搜索。每一步搜索，倘若其适应度优于[pbesti]则将其值赋给[pbesti]。搜索完[MS]步后，将[pbesti]的值存入到[gbest]中。

3.2.2 逃逸策略

PSO算法迭代若干次后，所有的粒子都会趋于[gbest]。如果当前[gbest]是一个局部极值，那么一旦所有粒子都收敛于这一点之后，这些粒子就很难跳出这个局极值点。为改善粒子生存密度，在PSO 算法的基础上提出粒子逃逸策略，获得更大的生存空间，从而提高算法的收敛速度和精度[9]。当算法运行过程中[gbest]连续[G]代无变化，需采用逃逸策略来产生新一代的粒子群。将原始一半种群保留，另一半采取式（14）的方式进行逃逸[10]。

[θijt+1=lj+ruj-lj]                  （14）

式中，[r]为[0，1]区间上的随机数，[θj∈lj，uj]。

3.3.3 改进的PSO算法的流程图

基于局部搜索和逃逸策略的PSO算法流程图如图3所示：

4 实验结果及分析

为验证基于PSO算法求解逆运动学问题性能的好坏，以及改进策略是否提升PSO算法的性能，选取如图4所示的开链式连杆结构的机器人进行测试，其位姿矩阵如式（15）所示的。

[W=-0.4698-0.3420-0.8138-0.5383-0.17100.9397-0.29620.01690.86600.0000-0.50002.06600001]           （15）

机器人的结构参数如表1所示，表2给出了算法改进前后的实验结果，图5分别显示目标函数在算法改进前后的收敛情况。

在两种算法中，粒子群规模[M=40]，维数[N=5]，学习因子[c1=c2=1.5]，最大迭代次数设为100，最小误差设为0.02，[θi∈-180?180]（[i=1，2，...，5]）。原始算法中的惯性权重[w=0.7]。在改进的算法中，惯性权重[w=0.9]，搜索步长[λ=0.2]，最大搜索步数[MS=4]，逃逸代数[G=5]。

表2的数据表明，PSO算法可以完成对逆运动学问题的求解。在加入局部搜索环节和逃逸策略后，解的精度得到很大的提升，并且加快了收敛速度。图5展示了两种算法的整个收敛过程。很明显，改进算法的曲线优于原始算法。

5 结论

本文利用PSO算法避开直接求解逆运动学问题，针对PSO算法中的不足提出改进策略。结果表明，改进后的PSO算法能够加快收敛速度改善计算精度，保证机器人逆运动学问题的实时性和准确性。

参考文献：

[1] Manseur R， Doty KL. Structural Kinematics of 6-Revolute-axis Robot Manipulators[J]. Mechanism and Machine Theory， 1996， 31（5）： 6472657.

[2] Eberhart R， Kennedy J. A new optimizer using particle swarm theory[C]. Proc Int Sym Micro Machine and Human Science： Nago2ya， Japan， Oct. 1995， 139- 43.

[3] 劉洪霞. 粒子群算法改进及应用[D]. 南宁： 广西民族大学， 2011：4-5.

[4] 郝武伟， 曾建潮. 基于聚类分析的随机微粒群算法[J].计算机工程与应用， 2010， 46（8）： 40-44.

[5] 龚纯， 王正林. 精通MATLAB最优化计算[M].北京：电子工业出版社， 2009.

[6] 陈宝林. 最优化理论与算法[M].北京： 清华大学出版社， 2005.

[7] （美）Saeed B. Niku. 机器人学导论——分析、系统及应用[D].北京： 电子工业出版社， 2004 .

[8] 任玉杰. 数值分析及其MATLAB实现[M]. 北京： 高等教育出版社， 2007.

[9] 谢铮桂， 钟少丹， 韦玉科. 改进的粒子群算法及收敛性分析[J].计算机工程与应用，2011， 47（1）： 46-49.

[10] 王志. 粒子群优化算法及其改进[D].重庆： 重庆大学， 2011： 9-10.

【通联编辑：唐一东】