浮式海洋热能转换系统的主动振动控制与扰动观测器设计

何修宇 王雪璇 赵哲惟 张爽

随着社会发展和世界人口的剧烈增长,能源问题逐渐成为国际上第一热点问题.为解决即将来临的化石能源枯竭问题以及日益严重的环境污染问题,人们转向对可再生的清洁能源的探索,例如,太阳能、风能、地热能、海洋能、潮汐能等.海洋占地球表面近70%,蕴含着极为丰富的能量,对于海洋能的开发吸引了越来越多的关注.

海洋温差能是一种典型海洋热能,资源蕴含量丰富,具有巨大的开发潜力.海洋热能转换系统(Ocean thermal energy conversion,OTEC)是一种能有效实现海洋热能–电能的能源转换系统[1−3].该系统利用海洋不同深度海水间的温度差,通过将冷海水输送到洋表和温海水进行冷热交换来驱动涡轮机产生电能并汇集到海底电缆传输到主输电网中[4].相比于其他可再生能源,OTEC 系统具有生产稳定、应用广泛等优点[5−6],此外,OTEC 系统在生产过程中还可以生成包括淡水、海洋营养物质等在内的副产物.综上所述,OTEC 系统具有良好的发展前景,并将在可见的未来得到广泛应用[7].

海洋热能转换平台通常需要安装在广袤的海上,远离海滨.相比于固定的生产平台,利用浮台或船只来安装转换装置具有很多的优势,它不仅生产灵活,能够随着海洋环境的变化而变更工作地点,而且安装成本低廉,维护便利.然而,在OTEC 系统所处的深海环境中,存在诸多的扰动,如:洋流、海浪以及向岸风等,另外,随着水深和管道重量的增加,用于连接海面浮台与下端镇重物,输送深层低温海水的柔性管道(上下跨度较大)可能会产生严重的形变以及剧烈的振动,这都将导致柔性管道的过早疲劳,甚至是损毁OTEC 系统,给生产和设备维护带来巨大的损失[8].现有的针对OTEC 的研究工作主要集中于发电效率的优化,抑或是平台结构力学方面的研究,而鲜有工作来研究用于输送海水的管道结构的振动抑制问题以及主动的振动控制设计.因此,如何设计有效的控制策略来解决OTEC 系统中柔性结构的振动问题对于深入研究OTEC 系统的研究具有一定的实际应用价值和理论指导意义.

从物理特性上来分析,OTEC 系统中的柔性管道因其大跨度特点,可以视为一个典型的欧拉–伯努利梁结构,即,柔性结构的横截面一直与中轴线垂直,柔性结构中的剪切形变量相较而言很小.根据其无穷维的物理特性而言,它是一个分布参数系统[9−14],通常用一组偏微分方程来描述其管道主体部分的动力学特性,以及用一组常微分方程来描述其边界位置的动力学特性[15].针对于分布参数系统的研究,主要是从两个方面着手,即,直接基于无穷维的系统模型[16−17]以及基于离散原系统后得到的有穷维模型[18−19].相比于后一种方法,直接基于系统的无穷维模型的方法在进行控制设计和稳定性分析时考虑了系统中所有状态量的动力学特性,常用的控制方法包括分布式控制和边界控制.它们由不同位置的信号组成并实施于不同的位置.在文献[20]中,作者研究了一类热传导方程,并基于系统的无穷维模型设计了分布式控制器来解决系统的温度变化问题以及系统中存在的全变量约束问题.然而,该控制器由分布式输出状态量构成并作用整个系统中,那么就需要无穷多个传感器和执行器来实现,显然对于实际的系统而言具有很大的实现难度.

另一类控制方法,即边界控制[21−24]是由系统的边界位置的信号组成,并最终作用于系统的边界位置上.相较于分布式控制而言,边界控制具有更好的可实施性.在之前的研究中,边界控制已经得到了一定的研究与应用.在文献[22]中,Endo 等在柔性机械臂的边界位置设计力控制器来控制柔性机械臂中的振动和角度位置.在文献[17]中,Do 研究了三维空间下海洋柔性输油立管的振动问题,设计一组边界控制器来减小柔性立管的三维结构振动.Paranjape 等运用基于backstepping 的边界控制策略来研究柔性机翼的机械振动抑制问题[25].在文献[26]中,Liu 等研究了一个空中加油机系统,通过在管道末端位置安装边界控制器来完成输油管道的振动抑制问题.除此之外,边界控制还被运用于其他的一些分布参数系统中[27−30].以上的系统通常只建立了一组偏微分方程来描述其自由运动端的动力学特性.本文的研究是针对两端自由运动的OTEC 系统来设计主动的振动控制器,柔性系统本身复杂的数学模型以及系统无穷维的特性使得该主动控制的设计变得相对困难.

在实际的工作环境中,OTEC 系统还可能会受到系统所处环境空间的限制,柔性结构中材料特性的限制或安全指标的限制等,这些限制的存在对系统的控制性能提出了更高的要求.如何在抑制OTEC 系统结构振动的同时,解决OTEC 系统中可能存在的输出约束问题也为主动振动控制器的设计带来了更大的难度与挑战.本文直接基于OTEC系统的动力学模型设计主动的边界控制器来分析闭环系统稳定性,抑制柔性管道的振动以及解决系统中存在的输出约束问题.

与之前的研究相比,本文的创新之处在于:1)在本文中分析了在外界扰动作用下OTEC 系统的动力学特性,建立了一个偏微分方程— 常微分方程组耦合的系统模型,并直接基于OTEC 系统的无穷维模型来进行主动控制器的设计,通过系统的边界位置信号来构成主动的边界控制器,从而有效地减小系统中柔性管道的结构振动;2)本文研究了OTEC 系统中可能存在的输出信号约束的问题,通过将对数障碍项引入系统的边界控制设计中来保证期望的边界输出信号不超出所给定的约束值,同时保证系统中浮式平台在初始位置的约束范围内运动.此外,还针对系统的外界扰动设计扰动观测器用以减小外界环境扰动对系统的影响.

本文结构如下:第1 节给出了浮式OTEC 系统的动力学特性分析以及建模,并用PDE-ODEs 耦合模型来描述OTEC 系统中柔性管道的动力学特性,另外还给出后文分析时所需要用到的预备知识.在第2 节中,详细描述了运用李雅普诺夫直接法进行主动边界控制律设计的过程以及系统稳定性的分析过程.在第3 节中,对浮式OTEC 系统做了几组数字仿真实验,来验证所设计控制策略理论证明的合理性.第4 节针对全文的研究工作做了总结和展望.

1 问题描述与系统建模

一个典型的浮式OTEC 系统主要由3 部分组成:能量转换平台、传输深层低温海水的柔性管道以及安装在柔性管道下端用于固定的镇重物体,如图1 所示.从OTEC 系统柔性管道的物理特性来看,可以将其视为一个典型的欧拉–伯努利梁结构.本文中,为了简化研究过程,只研究柔性管道在水平方向上的振动,多方向上的振动控制问题可以作为进一步的拓展研究.

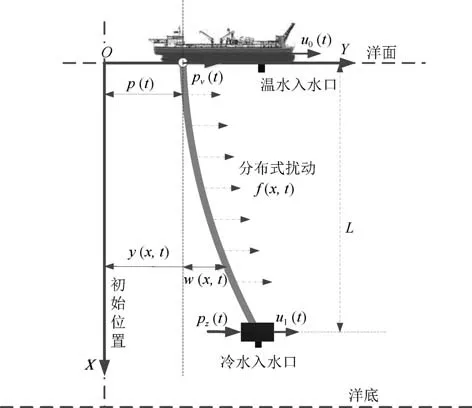
图1 典型的浮式热能转换系统示意图Fig.1 Floating ocean thermal energy conversion system

定义1.为了简化分析,对文中所用到的符号进行了简化,即,

对于柔性系统而言,哈密顿原理能够为系统提供一种确定动力学特性的有效方法.它是基于柔性系统的能量方程分析的,描述为

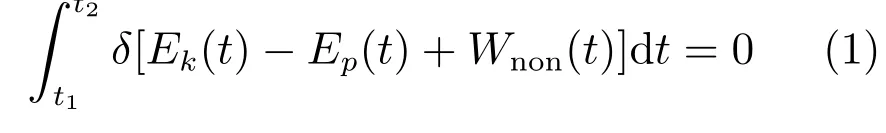
其中,δ是一个变分运算符,其他的能量项将在接下来的部分给出.OTEC 的系统动能Ek(t)描述为

其中,Ms和M0分别描述了OTEC 系统中柔性管道下端镇重物体和转换平台的质量,ρ描述了单位柔性管道的均匀质量.此外,p(t)和y(L,t)描述了OTEC 系统中柔性管道上下两端点的水平位移量,即,能量转换平台和镇重物体的位移.

OTEC 的系统势能Ep(t)描述为

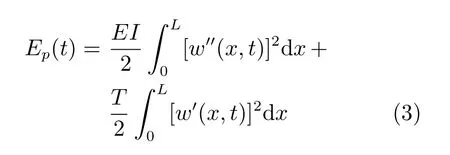
其中,EI描述了柔性管道的抗弯刚度,w(x,t)描述了OTEC 系统中柔性管道水平形变量,其与系统位移量的关系为y(x,t)=p(t)+w(x,t).T描述了柔性管道的张力.OTEC 系统所受到外界非保守力做的总虚功为

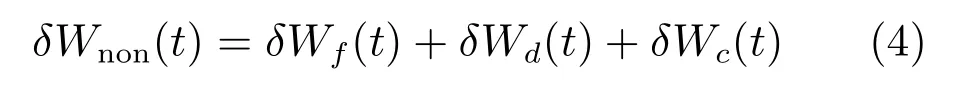
其中包括系统受到阻尼作用产生的虚功δWd(t)为

其中,c,d0和ds分别为柔性管道、转换平台和镇重物体上的阻尼系数.系统所受到外界环境扰动作用产生的虚功δWf(t)为

其中,f(x,t),pz(t)和pv(t)分别为作用在柔性管道、转换平台和镇重物体上的外界扰动.系统所受到设计控制力作用产生的虚功δWc(t)为

其中,u0(t)和u1(t)分别为作用在柔性管道上下端的控制作用力.

作用于OTEC 系统所有非保守力所做的虚功为

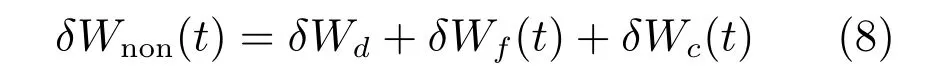
运用哈密顿原理,并结合式(2)∼(4)和式(8),可以得到系统的主控方程为

∀(x,t)∈(0,L)×[t0,∞),以及边界条件

∀t ∈[t0,∞).

假设1.假设OTEC 系统中柔性管道所受到的分布式扰动f(x,t)在L2[0,L]范数中是有界的,即

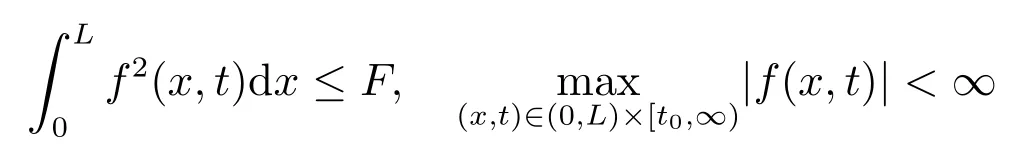
上式说明了环境扰动具有有限的能量.

假设2.对于OTEC 系统边界位置所受的海洋环境扰动pz(t)以及pv(t),假设它们是有界的,并且存在两个个未知的正实数Pz,Pv为扰动的界值,即|pz(t)| ≤Pz以及|pv(t)|≤Pv.

性质1[31−32].对于两个正实函数ψ1(x,t),ψ2(x,t),其中(x,t)∈[0,L]×[t0,∞),满足

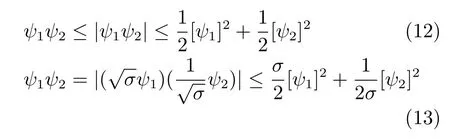
其中,σ是一个正的常数.

性质2[33].对于实函数ϕ1(t),其中,t ∈[t0,∞],下列不等式成立

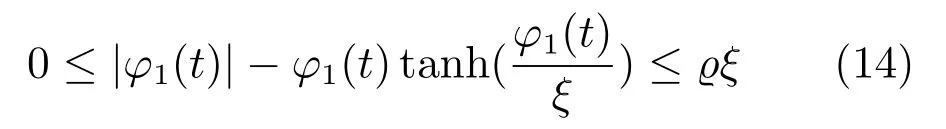
2 控制设计与系统稳定性分析

针对OTEC 系统,本文设计主动的边界控制器,用来减小柔性管道的弹性形变,补偿输入约束的非线性特性对系统的影响,保证系统的稳定.

构造李雅普诺夫函数为

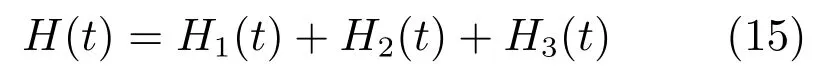
函数中各部分为

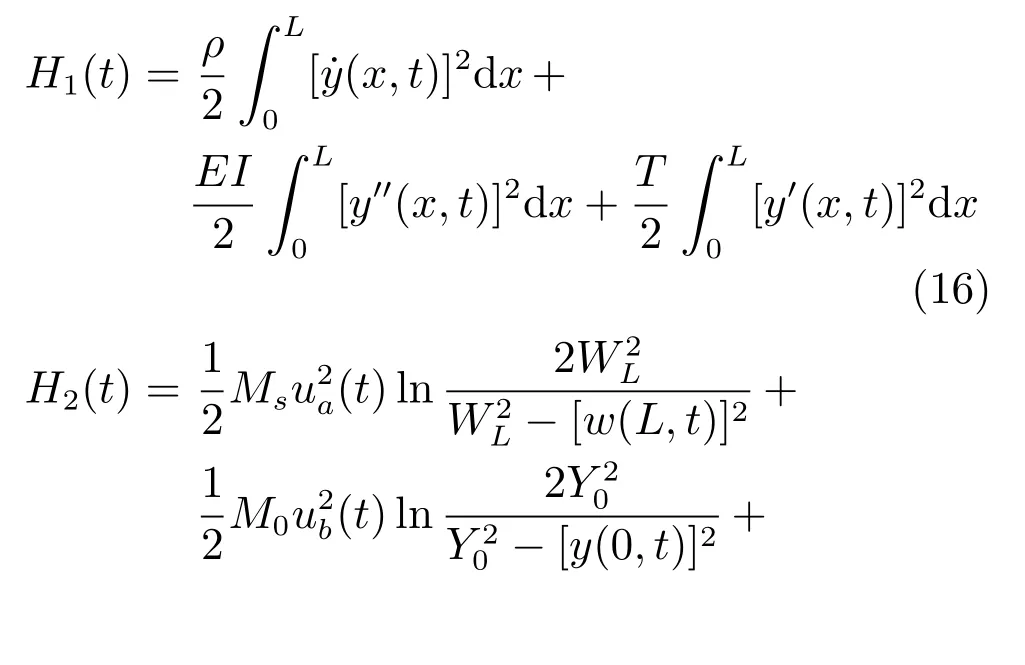
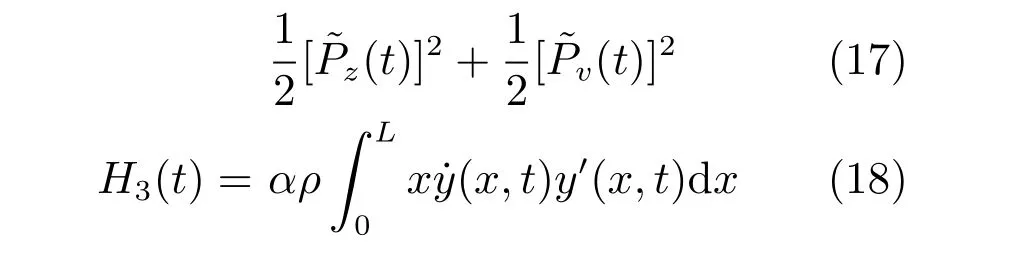
其中α是一个正常数.

H2(t)中的辅助函数由边界信号构成,定义为

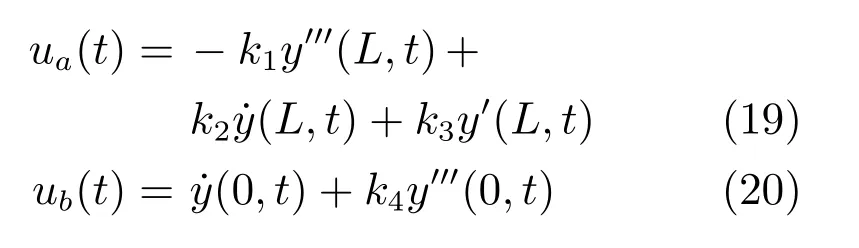
设计合适的边界控制律为

其中,ξ0和ξ1是两个正的常数.和是两个边界扰动观测器,分别设计为

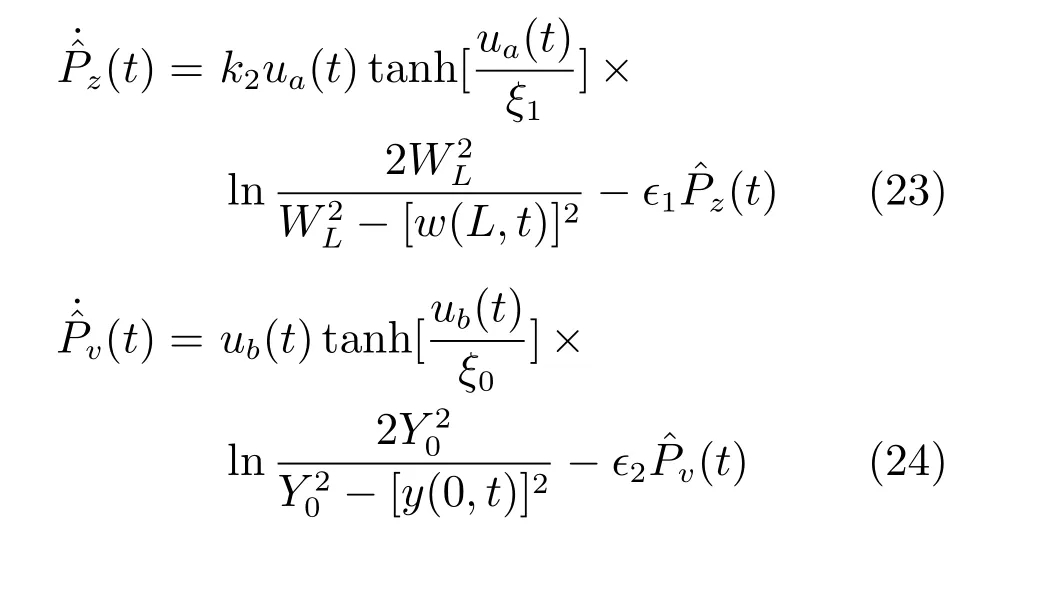
引理1.通过选择合适的参数,能够保证上文中所构造的李雅普诺夫函数(15)是一个有界的正函数,其上下界值表示为

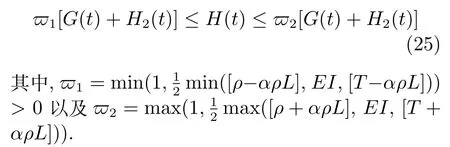
证明.构造一个函数G(t)为

运用性质1,将构造的函数H3(t)变形为

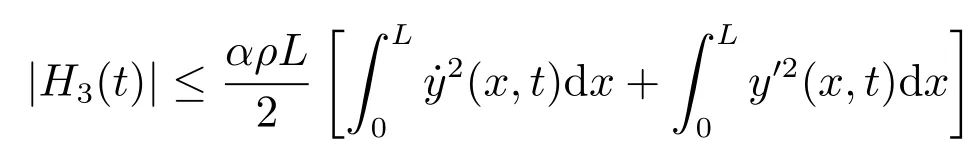
将上式展开并结合式(16)得

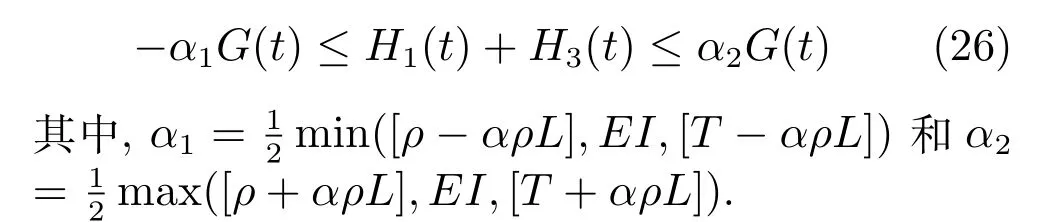
进一步,式(26)推导为

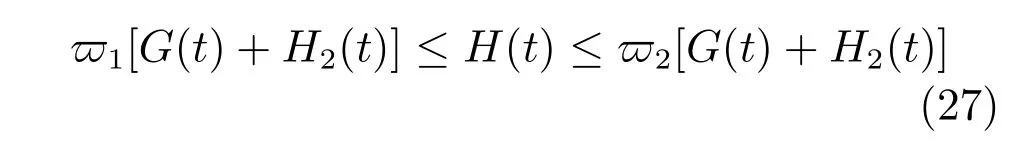
引理2.上文中所构造的李雅普诺夫函数(15)的时间导数是一个有界限的函数,其界值表示为

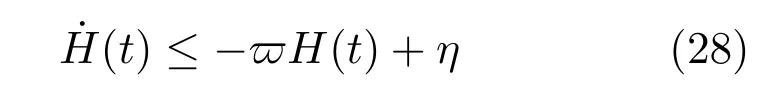
证明.对构造的李雅普诺夫函数求导为

其中,H1(t)的时间导数为

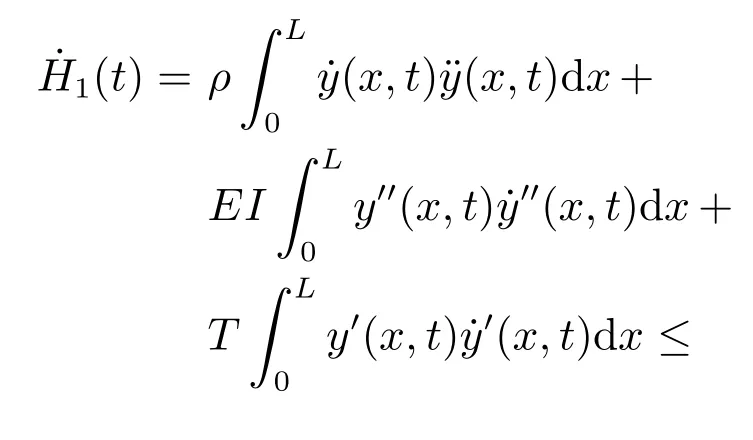
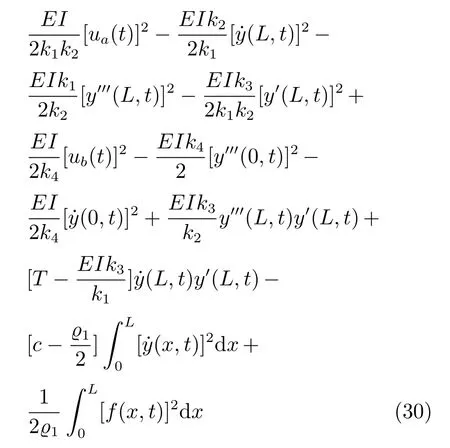
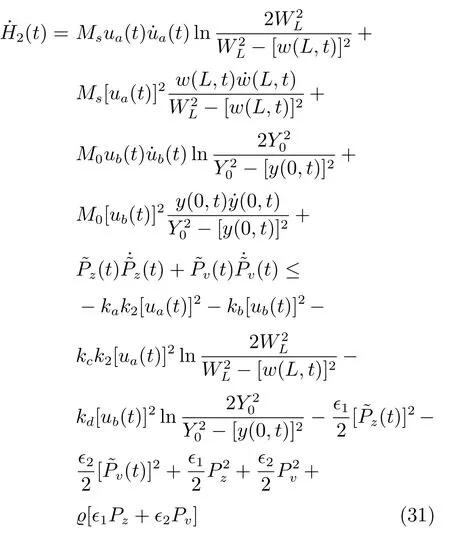
以及H3(t)的时间导数为

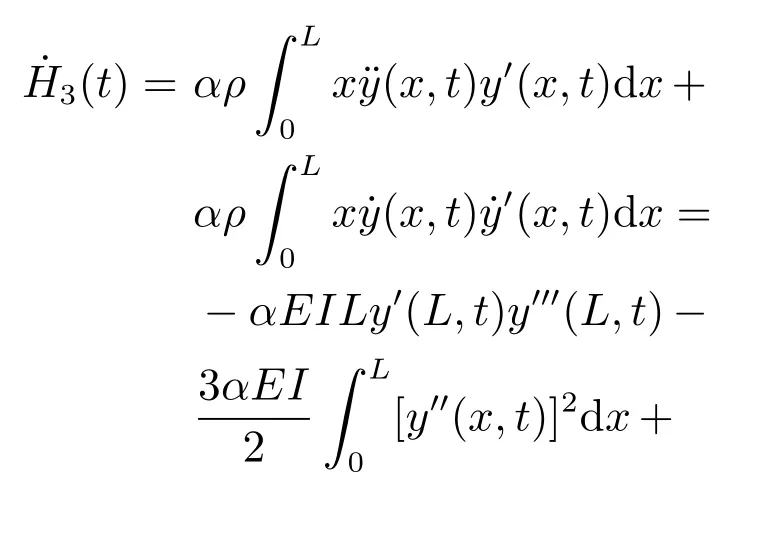
通过选择合适的参数k1,k2,k3,k4以及函数ϕ(x)使得下列式子成立

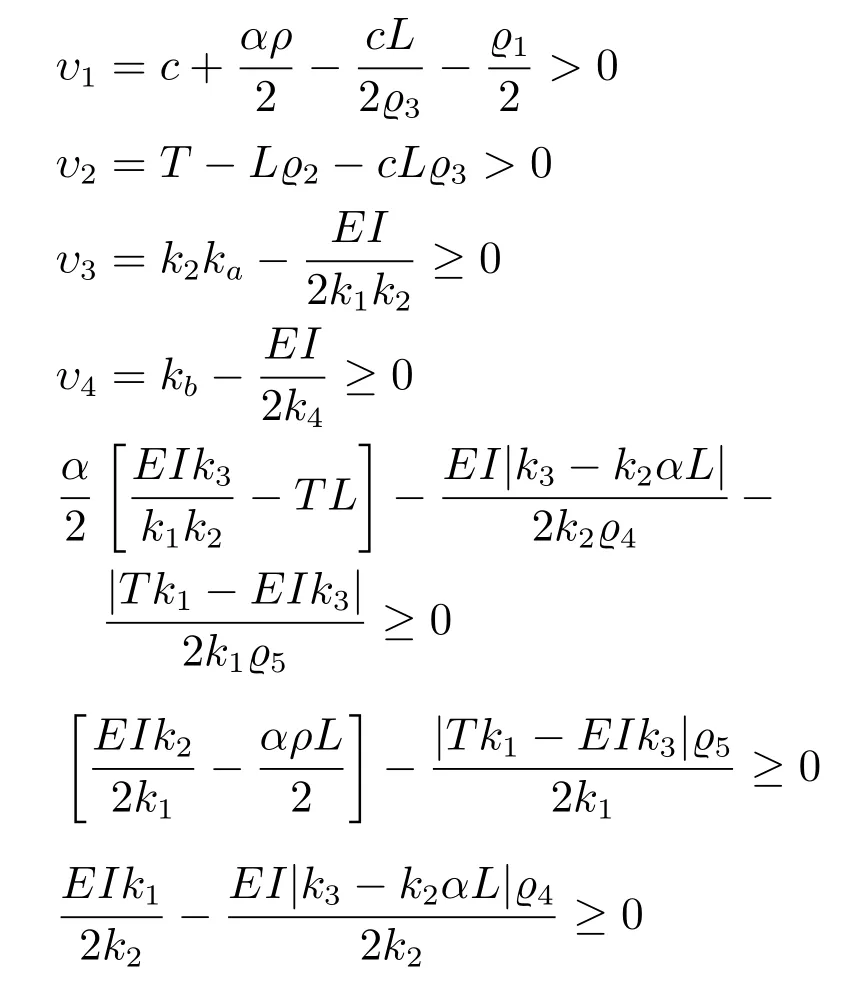
那么,可以得到

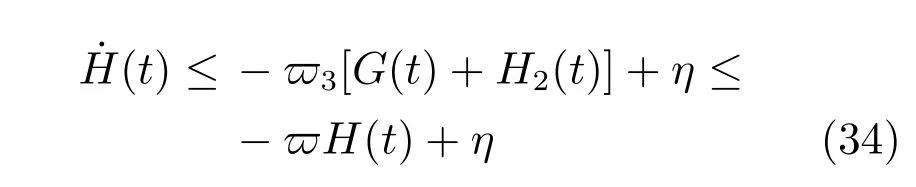
定理1.当柔性系统中的初始状态值有界时,基于有关外界扰动的假设1,我们可以得出OTEC 系统中柔性管道的弹性形变和振动减小,具体为

证明.将式(28)两端乘以并积分得到

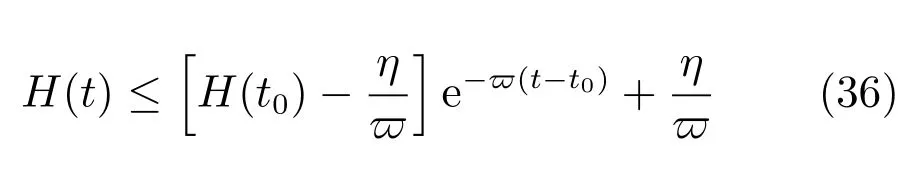
基于上式且运用性质2,关于OTEC 系统的弹性形变的不等式可以推导为

进一步地,上式变形为

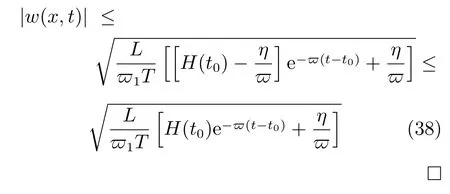
说明1.OTEC 系统中柔性管道的弹性形变最终收敛于系统的平衡位置附近,即

说明2.在上文中所设计的边界控制器(21)和(22)都是由柔性结构的边界信号做成,以及所有的组成信号都能由安装在柔性结构边界处的传感器检测或通过后向差分算法计算得到.信号y(L,t)和p(t)可以由激光位移传感器检测得到,(L,t)可以由倾角计检测得到,可以由剪切力传感器检测得到.此外,它们的时间导数信号可以基于检测的信号并通过后向差分算法计算得到.

说明3.由式(36)可以看出,H(t)是一个有上界的函数,那么,组成H(t)的正实函数H2(t)也是有界的,从该函数的表达式(17)可以推导知道期望的输出信号y(0,t),w(L,t)不会趋近所设定的约束值Y0,WL.如果系统中的边界初始值y(0,0),w(L,0)在所设定的约束范围内,那么,在上文所设计边界控制器(21)和(22)的作用下,所期望的输出信号y(0,t),w(L,t)就一直不会达到设定的约束界值Y0,WL,即,OTEC 系统中存在的输出约束问题得到了解决.

3 数字仿真

在上一节中,在OTEC 系统的两端设计了两个边界控制器,并通过理论的证明验证了所设计控制器的有效性.为了进一步地对设计控制器进行验证,我们将运用有限差分法(Finite differential method,FDM)来对OTEC 系统进行数字仿真,通过所得到的仿真结果来显示控制器的控制性能.在表1 中列出了OTEC 系统的各个参数,系统的初始值设定为y(x,0)=x/L以及˙y(x,0)=0.

OTEC 系统中所受到的分布式扰动f(x,t)借鉴之前的工作[34−35]直接给出

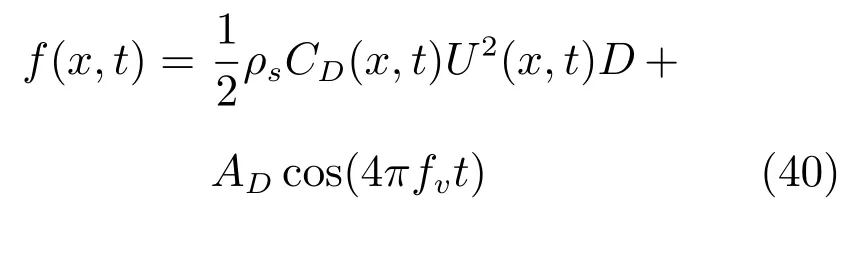
表1 浮式OTEC 系统的参数Table 1 Parameters of floating OTEC system

由上式可知,作用于柔性输水管上的分布式扰动f(x,t)由两部分组成,即,一个平均的作用力以及一个振荡的作用力,其中,ρs是海水密度,D为柔性管道的直径,CD为拉力系数.θ是相位角以及AD为幅值,其大小通常为分布式扰动中第1 项的20%.涡流频率fv表示为fv=StU(x,t)/D,其中,St为斯特劳哈尔数,时变海洋涌流U(x,t)和洋表涌流U(t)设定为

边界扰动pz(t)和pv(t)[36−37]设定为

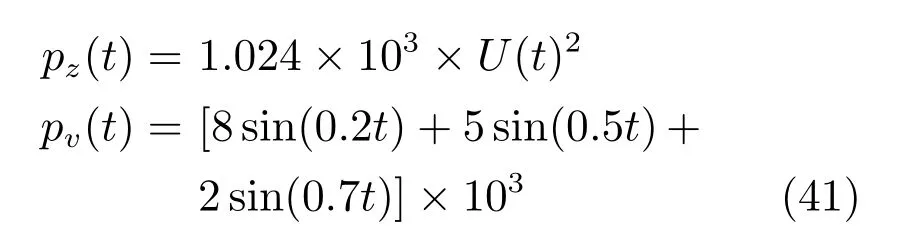
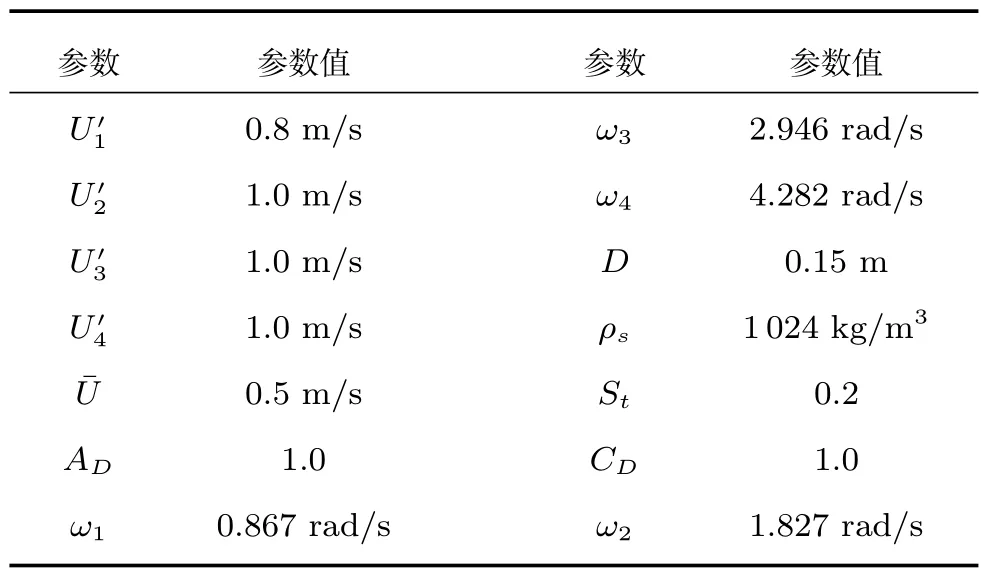
表2 扰动参数Table 2 Parameters of ocean disturbances

针对OTEC 系统并基于以上设定的环境与系统参数,我们将做3 组仿真实验,然后将3 组的仿真结果进行对比分析:

1)不施加控制.首先,在这种情况下,针对OTEC 系统不施加任何控制,即,u1(t)=u0(t)=0,得到了3 个仿真结果来描述系统的运动情况.通过描绘柔性输水管道运动的三维图(如图2 所示),我们看到柔性输水管道的呈现一个发散式的增长.通过观察结构两端位置的运动情况,如图3(a)和图4(a)可以看到,系统下端位置的振动也是呈现发散式增长,海洋表面的浮式平台漂移偏离了原始的位置.由以上的仿真图,我们可以看到该系统处于一个不稳定状态,不断增大的柔性结构振动可能会导致系统的损毁,同时,OTEC 系统在外界海洋扰动的影响下会偏离初始的位置.处于系统安全的考虑,需要提出有效的方法来减小系统的振动,保证系统的工作安全.

图2 不加控制器下的柔性输水管道的位移量Fig.2 Displacement of the flexible pipe without control

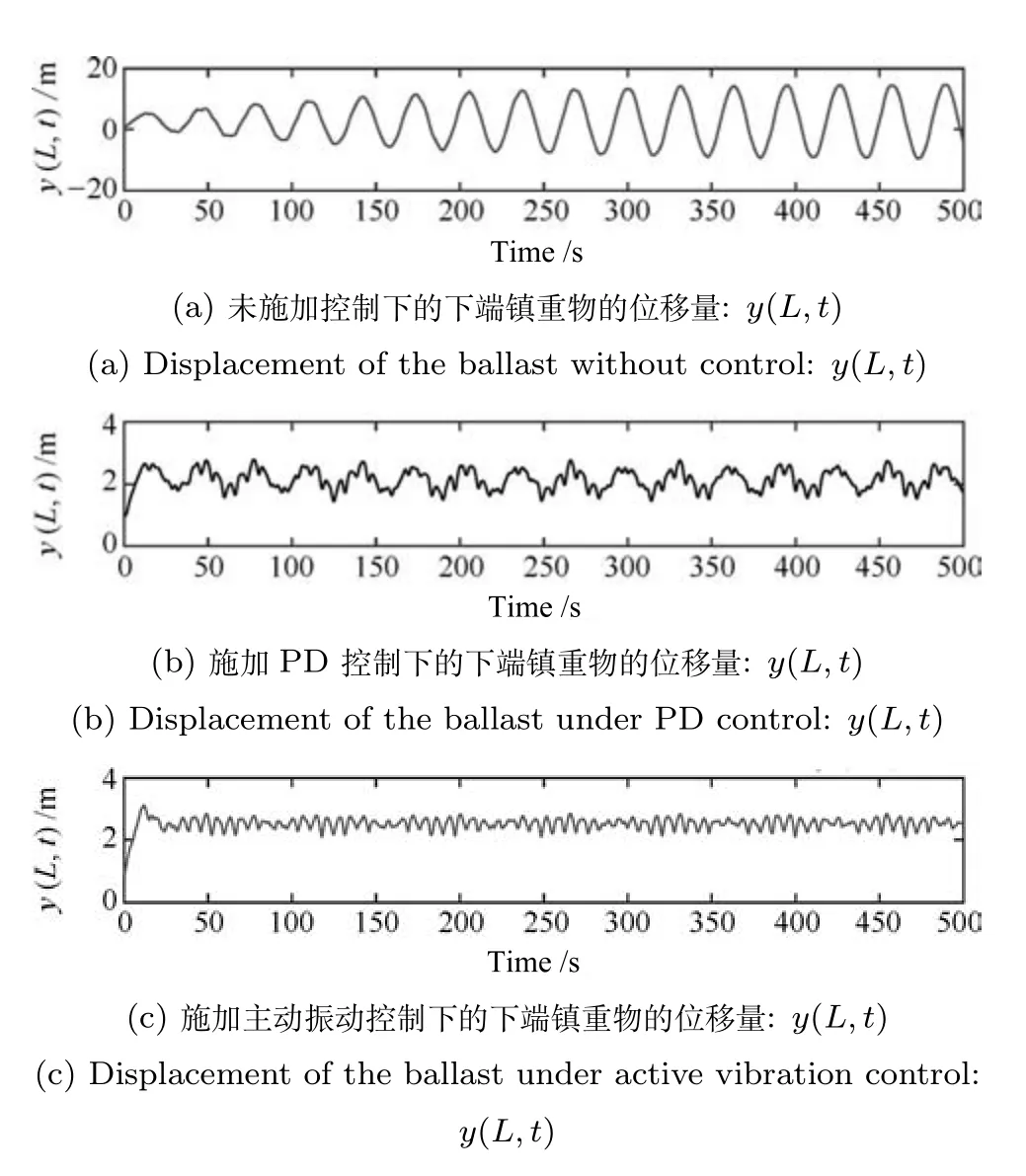
图3 柔性输水管道下端镇重物的位移量Fig.3 Displacement of the ballast

2)PD 控制.在工程中,比例–微分(Proportional-derivative,PD)控制器是十分常用的一种控制方法.在这种情况中,我们在柔性输水管道的端点位置施加典型的PD 控制器来分析其对系统振动抑制的情况.我们将该控制器设计为:u1(t)=−100×y(L,t)−100 000 ˙y(L,t)和u2(t)=−200y(0,t)−50 000 ˙y(0,t).同样地,我们得到了系统各位置运动情况的仿真图,从仿真得到的图5 和图3(b)可以看出,OTEC 系统中柔性结构的形变量得到了一定的减小.系统上端的浮式平台也被控制在原始点附近位置做类周期往复运动,如图4(b)所示.将这种情况与未施加任何控制的情况相比较,可以看到PD 边界控制器能够一定程度上保证系统的稳定性以及固定OTEC 装置平台的工作位置,但是效果并不特别理想.

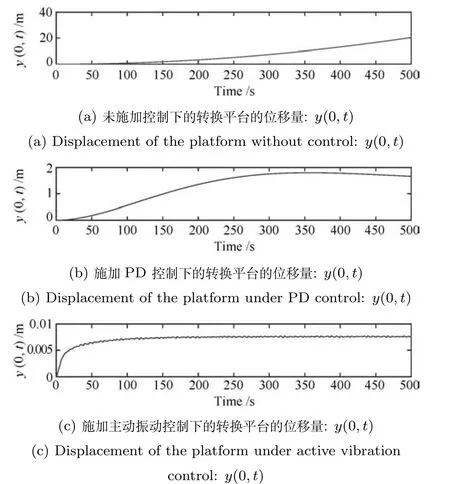
图4 上端浮式平台的位移量Fig.4 Displacement of the floating platform

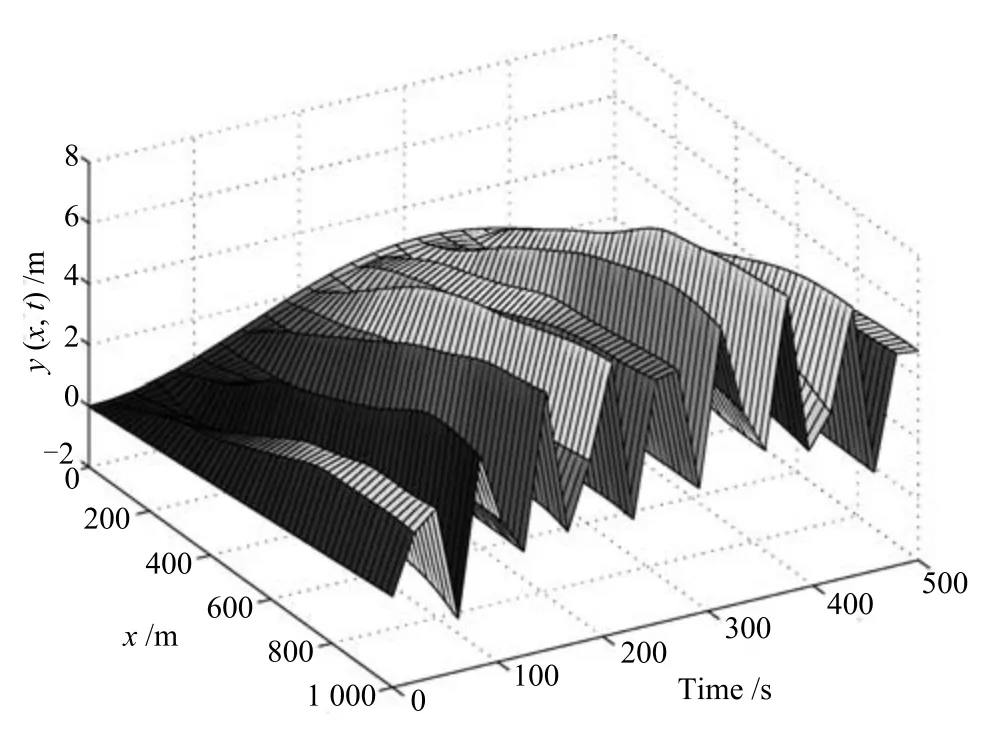
图5 施加PD 控制器下的柔性输水管道的位移量Fig.5 Displacement of the flexible pipe with PD controllers

3)所设计边界控制.在这种情况下,我们将设计主动边界控制器(22)和(21)施加到柔性输水管道上.通过上一节中确定的控制增益范围结合实际的仿真结果,选定各控制增益为:ka=0.01,kb=1 000,kc=106,kd=106,k1=500,k2=0.7,k3=155 以及k4=1.作为比较,我们也得到一个三维图和两个端点位置的运动图,图6 描绘了在本文所设计控制器的作用下,系统中柔性管道的形变量的变化情况,从图形的变化可以很容易地看出,柔性输水管道的形变量得到了减小.同时,系统中柔性管道的下端负载的形变量也减小到了零附近,如图3(c)图.除此之外,从图4(c)的下图可以看出,系统的浮式平台也在出现大幅振荡往复之后逐渐向初始位置运动.最后,给出了控制器的变化图,如图7 所示.

图6 施加所设计控制器下的柔性输水管道的位移量Fig.6 Displacement of the flexible pipe with the designed controllers

通过以上三种情况下系统动力学特性的相互比较,可以清楚地看到,构造的PD 控制器和本文所设计的控制器都能够减小由外界扰动引起的OTEC系统中柔性管道的剧烈振动.通过比较这两种控制器的控制性能,可以看到本文所设计的控制器具有更好的控制效果,能够得到更好的瞬态和稳态特性,此外,该控制器还能保证海洋表面系统的浮式工作平台固定在初始的工作点附近.总体上来说,通过仿真实验,得到了和理论分析一致的结果,从分析的结果中均可以看到所设计的主动边界控制能够有效地抑制OTEC 系统中的不良振动,保证系统的稳定.

4 结论

本文针对OTEC 系统中柔性管道的振动问题设计了主动的边界控制器,利用柔性结构边界位置的信号组成控制器并实施在边界位置上来抑制整段柔性管道的形变以及保证系统满足存在的输出约束问题.通过理论和数字仿真的分析与研究验证了所设计的振动控制器的有效性.然而,本文只是考虑了OETC 系统在水平方向的振动,忽略了柔性结构在其他两个方向的振动以及各方向上振动的耦合关系.三维空间下浮式OTEC 系统的振动研究是一个具有挑战性的工作.此外,对于浮式的平台,锚链常用固定洋表浮式平台,柔性管道结构和柔性锚泊结构的耦合也是今后能够继续研究的方向.此外,本文中所设计的边界控制是由可测量值构成.然而,在控制器的执行过程中可能还会存在超出最大功率等输入约束的影响,我们也将在接下来的工作中综合考虑输入约束对系统的影响以及进行设计抗输入约束的主动振动控制设计的研究.

图7 设计的主动振动控制力Fig.7 Designed vibration control forces