基于对偶四元数法的空间四连杆引纬机构运动学分析
2019-11-01金国光张旭阳
金国光,张旭阳,李 博
(1.天津工业大学机械工程学院,天津 300387;2.天津工业大学天津市现代机电装备技术重点实验室,天津 300387)
剑杆织机是目前工业上应用最广泛的无梭织机,它能适应各种类型的纱线,且具有较高的生产率。引纬机构是高速剑杆织机传动系统的重要组成部分[1],它将纬纱引入梭口,形成织物所需要的纹理。该机构由球面4R 机构带动平面四连杆机构,经齿轮放大机构实现剑杆的往复直线运动,进而实现引纬动作[2]。其结构形式、运动精度和动态性能直接影响到整个纺织过程的作业速度和加工精度,决定着织物的质量,对整个产品的生产效率和生产质量起到关键作用。目前,常见的引纬机构类型主要有共轭凸轮机构、空间连杆机构、变螺距螺杆机构、差动轮系连杆机构等。其中,空间连杆机构由于其结构简单、传动路线短、运转速度快等优点而被广泛地应用。
在针对连杆机构的运动学研究领域:TÜMER 等[3]建立了引纬机构的运动模型,并研究剑头工作范围与其速度的临界特性;EREN 等[4-5]根据剑头的位置,通过解析代数法建立了空间四连杆运动学模型,并分析运动变量对输出的影响;金国光等[6]利用软件对空间四连杆引纬机构进行有限元分析;袁汝旺等[7]提出了基于无急回特性的六连杆打纬机构,并给出了刚体导引与机构几何关系相结合的尺度综合方法;王品等[8]运用对偶四元数法对空间五杆机构进行位移分析,并通过实例验证,得出解析解的个数;徐永康等[9]通过矢量法分析了空间四连杆和平面四连杆的运动学,分析了主轴转速和驱动杆长对输出的影响;文献[10-11]利用三维软件对连杆机构进行了模拟仿真。
以上文献都分析了杆长变化对运动输出的影响。本文通过对偶四元数法[12-23]对空间四连杆机构进行运动学分析,得到不含杆长的运动学模型,结合工艺要求[24]分析机构夹角与运动输出的关系,以期为后续空间四连杆的优化设计提供参考。
1 空间四连杆引纬机构工作原理
图1 为剑杆织机空间连杆引纬机构简图。

图1 空间四连杆引纬机构简图Fig.1 Diagram of spatial four-bar linkage weft insertion mechanism
由图1 可以看出,空间连杆引纬机构由3 大部分组成:传动曲柄、空间连杆、十字摇轴组成空间传动部分;扇形齿轮、传动小齿轮和剑轮组成放大机构部分;剑带和剑头组成输出部分。传动曲柄连接在箱体上,在伺服电机的驱动下,匀速转动,带动机构运转。空间连杆将曲柄的匀速运动传递给十字摇轴,使十字摇轴在平面内做顺时针和逆时针的往复摆动。十字摇轴与扇形齿轮固连在一起,扇形齿轮做往复摆动,经过传动小齿轮和剑轮的放大后,传递到剑带上,从而带动剑头实现往复直线运动。
2 空间四连杆引纬机构运动学建模
图2 为空间四连杆的简图。

图2 空间四连杆简图Fig.2 Layout of 4R spatial linkage
图3 为由 4 个回转副 A、B、C、D 组成的空间连杆4R 机构的运动简图。
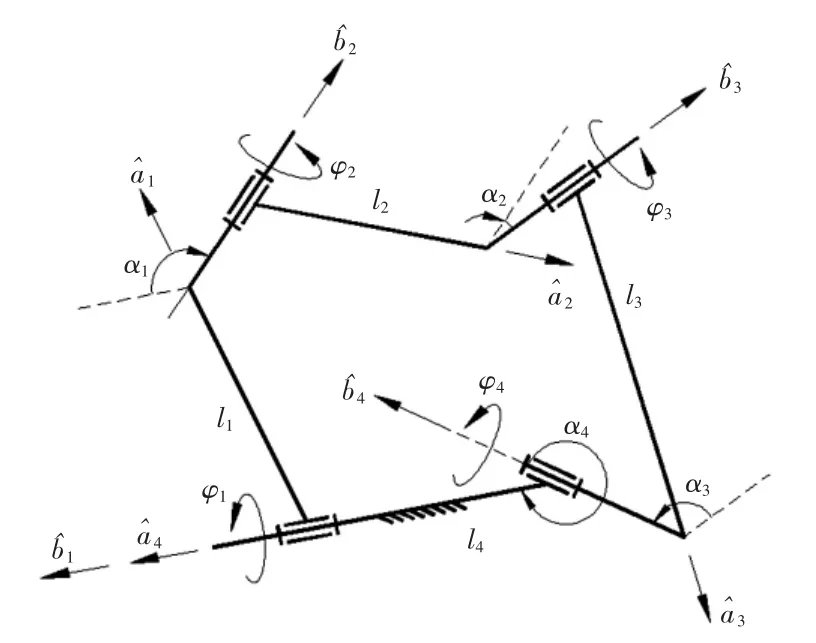
图3 空间4R 机构运动简图Fig.3 Kinematical sketch of 4R saptial linkage
图3 中,两相邻运动副之间的垂直距离为杆长,分别用 l1、l2、l3、l4表示;两相邻杆之间的垂直距离为副长,分别用 h1、h2、h3、h4表示;两相邻运动副之间的交错角称为该构件的扭角,分别用 α1、α2、α3、α4表示;φ1、φ2、φ3、φ4分别为两构件之间的相对转角;分别用对偶矢量表示运动副 A、B、C、D 轴线的空间位置;分别用对偶矢量表示各杆长方向的空间位置。各构件的扭角αi和运动副的转角φi见图3。


式中:i=1,2,3,4。
图3 中,将定坐标系设于机架 l4上,令根据式(1)可求得对偶矢量进而求出其逆变换利用关系可消除其他变量,得到只含有φ4的对偶方程:

根据机构参数可知,α1= θ,α2= β,α3= 90°,α4=270°。将 α1、α2、α3、α4代入式(3)中可得:
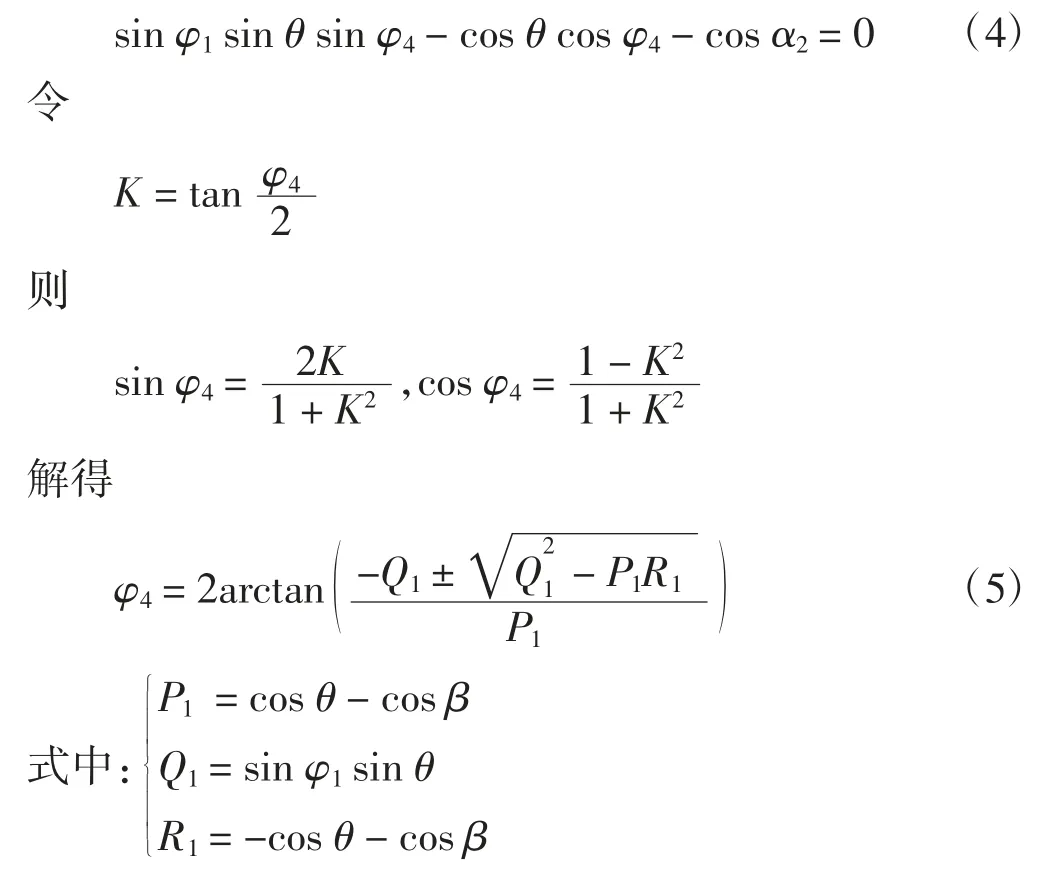
根据 φ4/2 < 180°可得,式(5)中±取+号,由-P1R1≥0 可得:β > θ。
齿轮机构为放大部分,设放大系数为m,则最终剑带的输出位移、速度、加速度为:

3 摇杆摆角与机构尺寸之间的关系
图4 所示为空间四连杆的极限位置。

图4 空间四连杆极限位置示意Fig.4 Limit position diagram of 4R spatial linkage
设机构初始运动时,杆AB 与轴线AD、杆DC、杆BC 在同一平面内,且B、C 两点在轴AD 的同一侧。根据机构的运动特性可知,驱动杆AB 转角为0°时摇杆的摆角φ4最小,转角为180°时摇杆的摆角φ4最大,分别对应图4 中的实线和虚线状态。
分别将 φ1对应的 0°和 180°代入到式(6)中可得:

经运算可得:

由图 4 可得出:BC=B1C1,BD=B1D,CD=C1D,进而证明了ΔB1C1D 与ΔBCD 全等,则∠BCD=∠B1CD1,∠CDC1=∠BDB1,∠CDC1=2θ,再次用几何法证明了连杆的摆角范围是机构夹角θ 的2 倍关系。保持AB杆和AD 杆的长度不变,变动BC 杆和CD 杆的长度只影响连杆的初末位置,但不影响连杆的摆角范围。根据这一特性,可对剑头的位置进行调整以适应不同的工艺要求。
4 机构参数对运动输出的影响
由运动学计算结果可以看出,剑带的运动特性与以下3 个参数有关:杆AD 与杆BD 的夹角θ;杆CD和空间连杆旋转轴线BD 的夹角β;放大系数m。当夹角θ和夹角β 为固定值时,放大系数m 与最终的运动输出呈线性关系,因此,本文不对齿轮传动系统做深入探讨。为使数值更具有清晰性,在此近似取m 的值为3 600/π,来研究夹角θ 和夹角β 对运动输出的影响。
图5 为剑杆织机实物。

图5 剑杆织机实物Fig.5 Rapier loom
图5 中,幅宽长度为0.9 m,引纬槽长为0.75 m,剑头长为0.23 m,故剑头的行程范围为0.9~1.42 m。考虑到误差的影响,为了保证剑头能安全有效进出,将行程范围设定为1.0~1.3 m,计算出对应的θ 值为50°~65°。
由工艺要求可知,引纬机构应具备以下特点:①剑头加速度最大峰值的绝对值要小;②加速度变化尽可能平缓,以减少冲击振动;③在夹持和交接纬纱时,要求剑头速度和加速度尽可能小,以增加夹持和交接的可靠性,减少失误;④整个机构要简洁,占用空间小,安装方便。
4.1 θ、β变化对剑头加速度的影响
根据以上要求,本文采用Matlab,分别绘制了θ、β和加速度最大峰值的关系,θ、β 和加速度方差的关系,θ、β 和交接纬纱时加速度的关系。根据实际生产,选取400 r/min 为主轴转速。
4.1.1 θ、β 和加速度最大峰值的关系
图6 所示为通过变化式(8)中夹角 θ 和夹角 β 的值来得到剑头的加速度,再通过MATLAB 函数所取得的剑头加速度的最大值。

图6 加速度的最大峰值Fig.6 Peak acceleration
由图6 可以看出,图像关于平面β- 90°=0 完全对称,这表明当夹角β 取两个不同的角度值且这两个角度互补时,剑头达到相同的最大加速度。保持夹角θ 的值不变,当夹角 β 的值从 50°增加到 90°时,剑头最大的加速度值越来越小,根据对称性,当夹角β 的值从90°增加到130°时,剑头最大的加速度值越来越大。保持夹角β 的值不变,当夹角θ 增长的同时,剑头加速度的最大值也随之增长。当夹角β <80°且夹角θ >70°时和夹角 β > 100°且夹角 θ > 70°时,加速度的最大值增幅较大,为图6 中最陡峭的区域。图6 中的最小点在(θ,β)=(50°,90°)处,此处对应的加速度最大值为1 156 m/s2。
4.1.2 θ、β 和加速度方差的关系
图7 所示为通过变化式(8)中夹角 θ 和夹角 β 的值来得到剑头的加速度,再通过Matlab 函数所得的剑头加速度在引纬机构运行一个周期内的方差。

图7 加速度的方差Fig.7 Acceleration variance
图7 的图像关于平面β-90°=0 完全对称,此趋势和图6 相同,这一结论也表明了当剑头的加速度最大值增加的同时,剑头在一个周期内运行的加速度也相应地增加。图7 中最小点同样落在(θ,β)=(50°,90°)处,在这一点上,剑头加速度在引纬机构运行一个周期内最平稳,产生的冲击碰撞也最小。
4.1.3 θ、β 和交接纬纱时加速度的关系
图 8 为通过变化式(8)中夹角 θ 和夹角 β 的值来得到剑头的加速度,再通过Matlab 函数得到的剑头在引纬交接处的瞬时加速度。

图8 交接纬纱时的加速度Fig.8 Acceleration at weft yarn transferring
由图8 可以看出,当夹角θ 接近夹角β 时,交接纬纱处的剑头加速度较小;当两个夹角的差值增大时,交接纬纱处的剑头加速度也逐渐增大。剑头加速度的最小值位于直线θ = β 附近,这一趋势和图6、图7相反。图 8 中的剑头加速度最小点选在了(θ,β)=(51°,52°)。
根据以上分析,在3 个图像中选取2 组数据进行对比。第一组数据是加速度方差最小点和加速度最大值最小点(θ,β)=(50°,90°)和交接纬纱处的加速度最小点(θ,β)=(51°,52°);第二组数据根据图6 和图7 的对称性选择了两图中的共同最小点(θ,β)=(50°,90°),关于平面 β-90°=0 对称的两点(θ,β)=(50°,80°)和(θ,β)=(50°,100°)。
4.2 最优点处的运动特性分析
图9 为将选取的第1 组数据的数值代入式(6)、(7)、式(8)中得到的图像。图9 中实线为点(θ,β)=(50°,90°)所对应的运动输出,此处为加速度最大值最小点和加速度方差最小点;虚线为点(θ,β)=(51°,52°)所对应的运动输出,此处为交接纬纱处加速度最小点。

图9 最优点处的运动特性曲线Fig.9 Motion characteristics curves of best points
由图9 可以看出,虚线在主轴转角为100°附近时达到交接纬纱处附近,且在主轴转角为100°~260°时,剑头的位移、速度、加速度接近为0。由工艺要求可知,较小的剑头速度和剑头加速度有利于提高交接纬纱时的可靠性,但是虚线部分在主轴转角为90°~120°时,剑头的速度和加速度变化较快,所以在此区域内,剑头对纱线产生较大的牵引力,增大了小强度纱线被扯断的几率。
4.3 β变化时的运动特性分析
图10 为变动β 时运动曲线的变化。
由图10 可以看出,选取θ=50°,3 条线的最大位移均相同,再次验证了第3 节的关系证明;β = 80°和β = 100°时速度和加速度的峰值相同,在纬纱交接处β = 80°时的加速度比β = 100°时的加速度小,但在交接纬纱附近处,以转角120°到 240°为范围界限,β =80°时的加速度变化比较大,比β = 100°时大了近28.57%,这表明其交接纬纱时的可靠性不如β=100°时好。

图10 β 变化时的运动特性曲线Fig.10 Motion characteristics curves as β changing
5 结 论
(1)用对偶四元数法建立了空间四连杆的运动学模型。该方法几何概念清晰,应用方便。与代数解析法不同的是,解析法建立的是杆长与输出的关系,对偶四元数法建立的是角度与输出的关系,从而可以从角度方面分析运动规律。
(2)分别用几何法和代数法分析了摇杆摆角与连杆夹角之间的关系,得出了摇杆摆角范围是机构夹角θ 的 2 倍的结论。
(3)结合工艺要求,分别绘制了运动变量与指标之间的关系。挑选了两组特殊点进行运动趋势分析,结果表明β=80°时的交接纬纱加速度变化比β=100°时大了近28.57%,这一结论为多目标优化时各目标权重的选取提供了一定参考。
