基于超启发式算法的选址-路径问题研究

(浙江工业大学 计算机科学与技术学院，浙江 杭州 310023)

选址-路径问题(Location-routing problem, LRP)将选址分配问题(Location allocation problem, LAP)与经典车辆路径问题(Vehicle routing problem, VRP)进行组合研究，属于经典的NP难问题。随着全球气候变暖，低碳问题得到了越来越多人的重视，而物流业是碳排放的主要来源之一，因此对于低碳物流模型的研究日趋增多。在模型上，曹剑东等[1-2]以总成本最小化为优化目标研究了考虑碳排放因素的车辆路径问题(Vehicle routing problem，VRP)。在求解算法上，基本以遗传算法、禁忌搜索等启发式算法居多，但这些算法不具有良好的通用性，无法适用于新研究出来的模型。

超启发式算法[3](Hyper-heuristic algorithms)是近年才发展起来的一种新型的启发式算法，可以简单阐述为“寻找启发式算法的启发式算法”，该算法具有良好的通用性，可用于求解排课问题[4]、流水车间调度问题[5]和装箱问题[6]等约束较少的组合优化问题。超启发式算法的研究主要集中在选择策略、接收策略和底层算子三部分。文献[7]研究了针对旅行锦标赛问题的基于蚁群的超启发式算法，采用蚁群算法来管理和操纵LLH以获得新的启发式算法，每只蚂蚁均构造一个新的启发式算法。Marshall等[8]将语法演化应用在超启发式算法中，使其产生良好的解，通过仿真实验，对40 个著名的车辆路径问题进行仿真，取得了不错的结果。国内外关于超启发式算法在低碳LRP模型中的应用研究甚少，笔者将基于蛙跳算法的选择策略用于启发式算法对低碳LRP问题进行求解，并提出了基于最长公共子序列的相似度计算方式。

1 问题描述

1.1 低碳LRP模型

本实验采用的模型[9]为多个配送中心使用单一类型车辆为每个客户点配送货物，不考虑时间窗、车辆最大行驶距离等约束条件。此问题描述为：有n个客户点需要配送货物，有M个仓库点进行发送货物，每个仓库都只有一种类型的车，车的载重都为Qk。每个客户点都由某一个仓库点进行货物发送，每一辆车都从仓库出发，前往每一个客户点去送货，直至送完所有货物，最后返回仓库。具体详情见表1。

表1 符号与变量说明Table 1 Explanation of variable and symbol

目标函数为

(1)

约束条件为

(2)

(3)

(4)

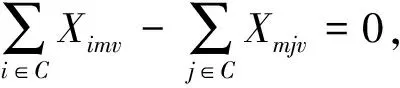
(5)

(6)

式(1)是LRP模型中车辆碳排放量的计算方法，即所有车辆完成配送任务后所产生的碳排放量，也是本实验的目标函数，是在张春苗等[9]所提计算方法的基础上取消了配送中心开放的固定碳排放量，增加了每一辆车的固定碳排放量，以鼓励减少车辆的使用；式(2)表示车的货物总量总是小于车的载重；式(3)保证每个配送中心访问的顾客总需求小于配送中心的容量；式(4)保证每个客户均被访问一次；式(5)保证每一辆车从配送中心出发最终又回到配送中心；式(6)保证每一个客户点的需求都被满足。

1.2 算子介绍

根据超启发式算法的特点，底层启发式算子属于问题域，由应用领域的专家所提供。在低碳LRP模型中，根据文献[10]，笔者采用的底层启发式算子为

LLH1：2-opt算子。选择一条路径，客户数量为N，从前N-1个客户中随机选举一个客户，将这个客户点和其后面相邻的客户点进行交换。

LLH2：or-opt算子。选择一条路径，客户数量为N(N>2)，随机选取相邻的两个客户点，将这两个客户点随机插入到该路径的其他位置。

LLH3：shift算子。选择两条路径，从第一条路径中，随机选取一个客户点，将它插入到第二条路径合适的位置。

LLH4：Interchange。选择两条路径，随机从两条路径中各选取一个客户点进行交换。

LLH5：配送中心的shift算子。选择一条路径，给这条路径设置一个新的配送中心。

LLH6：配送中心的Interchange算子。选择两条路径，交换它们的配送中心。

LLH7：Location-based Radial Ruin。选择一条路径，随机选举其中一个客户点，将此客户点作为基准客户，根据每个客户和基准客户的欧氏距离来重新生成解。

LLH8：Interchange*。与之前的Interchange算子一样，只不过此算子只接受改进解。

LLH9：shift*。与之前的shift算子一样，只不过此算子只接受改进解。

LLH10：2-opt*。与之前的2-opt算子一样，只不过此算子只接受改进解。

2 基于蛙跳算法的选择策略

选择式超启发算法根据反馈机制来源不同，可以分为不学习、离线学习和在线学习3 种，而在线学习机制又可分为基于元启发、基于强化学习和基于函数选择3 种选择方法，笔者使用了蛙跳算法(SFLA)来选择底层启发式算法，是在线学习机制中基于元启发选择方法的一种。SFLA模拟青蛙寻找食物的过程，是一种新型群智能进化算法，它是由Eusuff和Lansey[11]于2003年首次提出，并应用在求解水资源网络的管径选择和管网扩张问题中。笔者提出一种基于SFLA的上层选择策略，将蛙跳算法应用在选择式超启发，其框架如图1所示，在原有的基本框架上，加入了SFLA算法用于低层启发式算法的选择，同时根据应用算子后的结果反馈于SFLA算法。

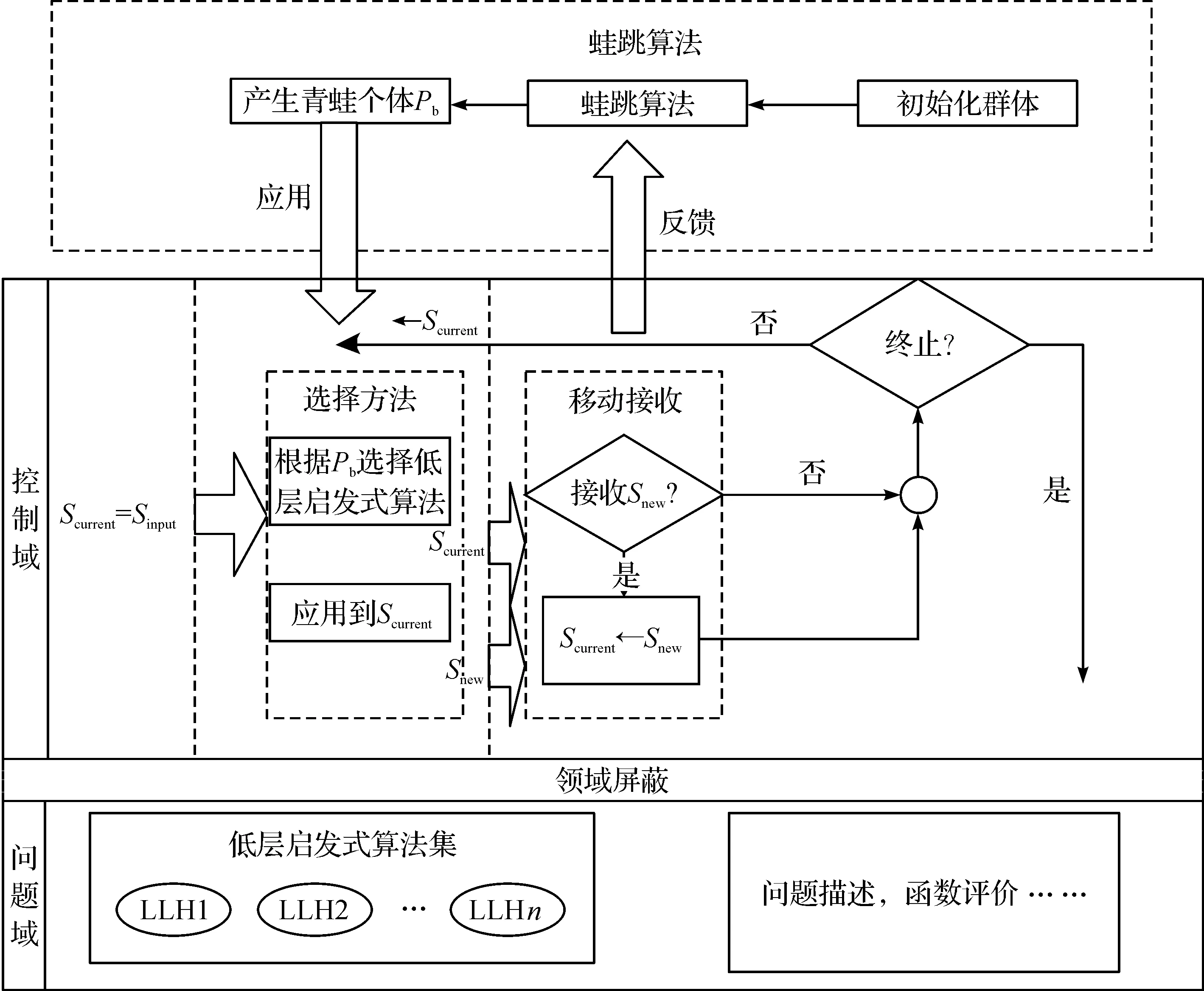
图1 基于蛙跳算法的选择策略框架Fig.1 Framework of hyper-heuristic algorithm in leapfrog algorithm

2.1 算法流程

算法的具体流程为

步骤1初始化参数。确定蛙群的数量、种群以及每个种群的青蛙数。

步骤2随机产生初始蛙群，计算各个蛙的适应值。

步骤3划分种群。

步骤3.1随机找寻一个解，计算其他解与它的相似度，按相似度划分种群。

步骤3.2重复步骤3.1，直到种群划分结束。

步骤4根据SFLA算法公式，在每个族群中进行元进化。

步骤4.1对全局最优和局部最优进行随机扰动。

步骤4.2对操作后的解计算适应度，如果有更优解出现，则进行更新。

步骤4.3重复步骤4.1和步骤4.2，直至达到预设循环次数。

步骤5将各个族群进行混合。在每个族群都进行过一轮元进化之后，将各个族群中的蛙重新进行排序和族群划分并记录全局最好解Px。

步骤5.1利用更新策略对局部最差解进行替换。

步骤5.2如果达到迭代次数则停止，转步骤6；如果没有，则转步骤3。

步骤6输出全局最优解。

算法流程图如图2所示。

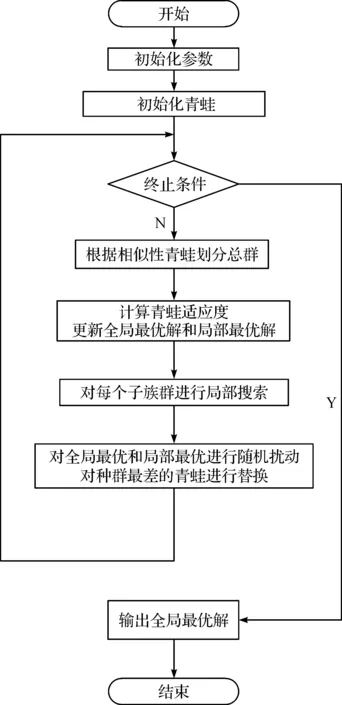
图2 蛙跳算法流程图Fig.2 Flow chart of leapfrog algorithm

2.2 编码解码和算法参数

由于笔者所提及的蛙跳算法是作为选取算子的高层策略，所以搜索到的空间不是车辆路径的解空间，而是算子的组合空间。如图3所示，这是一个青蛙个体，是由一串数字组成，每一个数字对应着各自的底层算法，例如数字1就代表着2-opt算子，即对解执行2-opt算子。一个解从最原始的状态进过一个青蛙个体之后，就会产生一个新的解，新的解的目标函数就是该青蛙个体的适应值。与其他优化算法一样，SFLA也具有一些必要的计算参数：F为蛙群的数量；m为族群的数量；n为族群中青蛙的数量；Smax为最大允许跳动步长；Px为全局最好解；Pb为局部最好解；Pw为局部最差解；q为子族群中蛙的数量；LS为局部元进化次数；SF为全局思想交流次数等。

3536114…6891

图3 青蛙个体示意图

Fig.3 Diagram of frog individual

2.3 更新策略

笔者更新策略采用文献[12]提出的方法，具体为对比每个种群内局部最优和局部次优解，如果相同位置上有相同的算子编号，则对该位置进行记录。推测该位置上的算子编号很可能是有利于增加适应度的，即有利于调度的，所以将种群内最差解位置上的算子编号替换为记录的算子编号。该操作如图4所示，一共为4 串数字，也就是4 个个体，第一行为全局最优解Px，第二行为子群最优解Pb，第三行是子群最差解Pw，第四行是更新后的Pw。

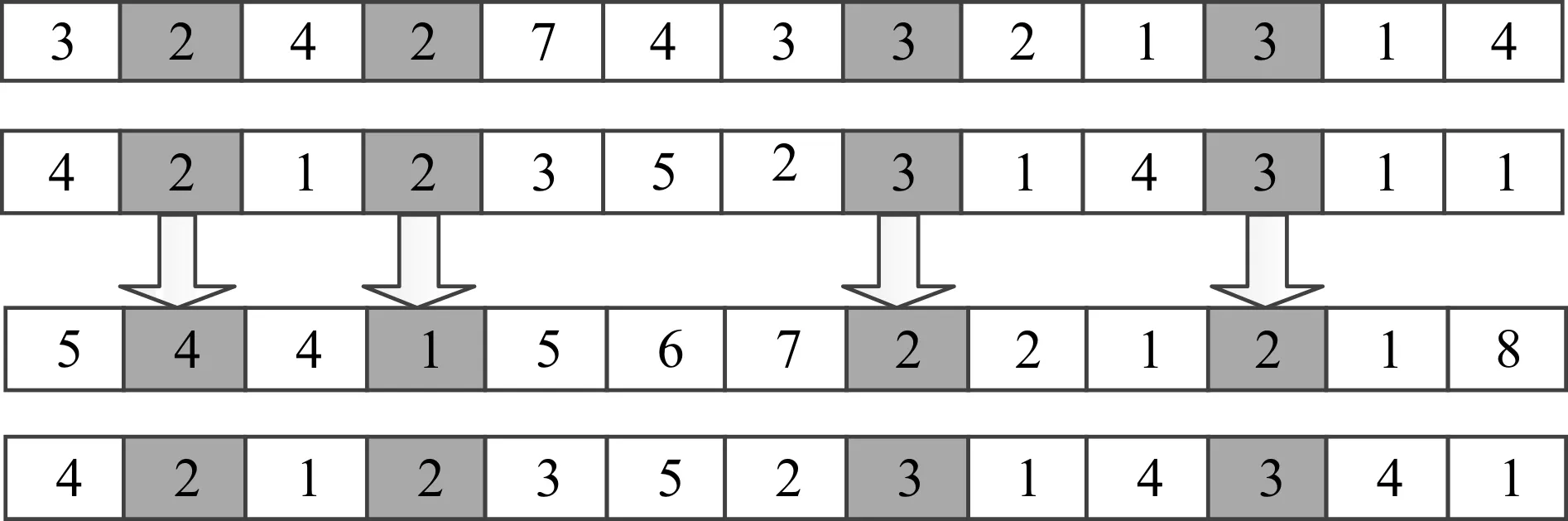
图4 更新策略示意图Fig.4 Diagram strategy of update strategy

2.4 改进的种群相似度计算方法

算法开始时随机初始化总数量的青蛙，即随机生成总数量的具有固定长度的一组数字，每个数字都代表一种底层启发式算子。在常见的SFLA算法中[13-16]，青蛙按适应度进行排序，以特定的划分原则进行种群划分。文献[12]提出了一种新的个体相似度定义，其算法是对比两个个体每一位上的数字，如果相同，则相似度加1。如图5所示，图5中两个解的相似度为3。

图5 相似度计算示意图Fig.5 Diagram of similarity computation

相比于传统的个体相似度计算方式，笔者提出了基于最长公共子序列的相似度算法，将该相似度算法应用在超启发式算法的上层策略中是本研究的主要创新点。所谓的最长公共子序列(LCS：longest-common-subsequence problem)是一个在一个序列集合中(通常为两个序列)用来查找所有序列中最长子序列的问题。一个数列，如果分别是两个或多个已知数列的子序列，且是所有符合此条件序列中最长的，则称为已知序列的最长公共子序列。例如以下两串编码“123456”和“234567”，根据文献[12]的相似度计算，它们的相似度为0，然而事实上它们其实十分相似，只是前者比后者一开始先调用了1次“1”算子，后者比前者最后多调用了1次“7”算子。根据最长公共子序列的相似度计算，前者有子串“23456”和后者的子串“23456”是完全一样的，所以它们的相似度为5，可以明显地看到采用公共最长子序列进行相似度计算能更好地还原两只青蛙的相似性。

因LCS问题的具有最优子结构性质[17]，最长公共子序列计算公式为

根据上述的递归公式和初值，有如下伪代码和实现：

输入两个青蛙个体

输出两个个体的相似度

步骤1function LCS(x,y,i,j)

步骤2if (x[i]=y[j])

步骤3thenc[i,j]=LCS(x,y,i-1,j-1)+1

步骤4elsec[i,j]=max{LCS(x,y,i,j-1)，LCS(x,y,i-1,j)}

步骤5returnc[i,j]

因此采用最长公共子序列的算法对图5的两个数组进行相似度计算，结果如图6所示。最长公共子序列为“4232314”，所以两只青蛙的相似度为7。

图6 最长公共子序列相似度计算示意图Fig.6 Diagram of similarity computation base on longest common subsequence

根据新的个体相似度计算方法，进行种群划分：

步骤1随机找到一个解，计算该解与其他解的相似度，按相似度从高到低选取n个解，划分成一个种群，其中n=青蛙总数(F)/种群个数(m)。

步骤2在剩余解中随机找寻一个解，利用步骤1的方法进行种群划分，直至种群划分结束。

3 数值仿真与分析

3.1 实验设计和参数分析

为了验证算法的实用性，对基准样例进行仿真实验，包括了5 个配送中心，20 个客户点，其中每个配送中心的坐标、库存量已知，每个客户点的坐标、需求量已知，配送中心的车辆载重已知，样例详细信息见网址[18]。基于蛙跳算法上层选择策略的超启发式算法，采用Cplusplus编程，运行在CPU为Intel Core i7，4.0 GHz，RAM为8 G内存的计算机平台上，考虑到蛙跳算法很多参数可能会对性能造成影响，根据文献[12]的结论，采用如下具体参数：青蛙总数Population=200，种群数量Group=20，个体长度Individual=20，迭代次数Maxloop=20。因采用新的更新策略，所以蛙跳算法中的最大允许跳动步长(Smax)等参数将不存在。

笔者提出的核心创新点就是SFLA算法中的相似度计算的改进，由原来的个体每一位相比较改为基于最长公共子序列的相似度计算。为了验证笔者提出的相似度计算方法的有效性，设计了两个对比算法。

1) SFLA：最基本的蛙跳算法，相似度即个体的适应度。划分总群即按相似度从高到低依次分配到每个子群。

2) SFBE(SFLA base each dimension)：由2.4节所描述的根据每个个体每一位上是否相等来计算相似度。

3) SFBL(SFLA base longest common subsequence)：笔者提出的基于最长公共子序列的相似度计算。

3.2 结果分析

首先对SFLA算法、SFBE算法和SFBL算法在解决低碳LRP模型的性能进行比较，通过收敛代数和目标函数收敛情况这两个方面进行分析。

3.2.1 收敛代数分析

3 种算法对LRP模型求解的收敛代数见表2，取运行10 次的平均收敛代数，这里迭代次数不设置为20，而是采用连续5 次迭代不出现更优秀个体作为终止迭代条件。

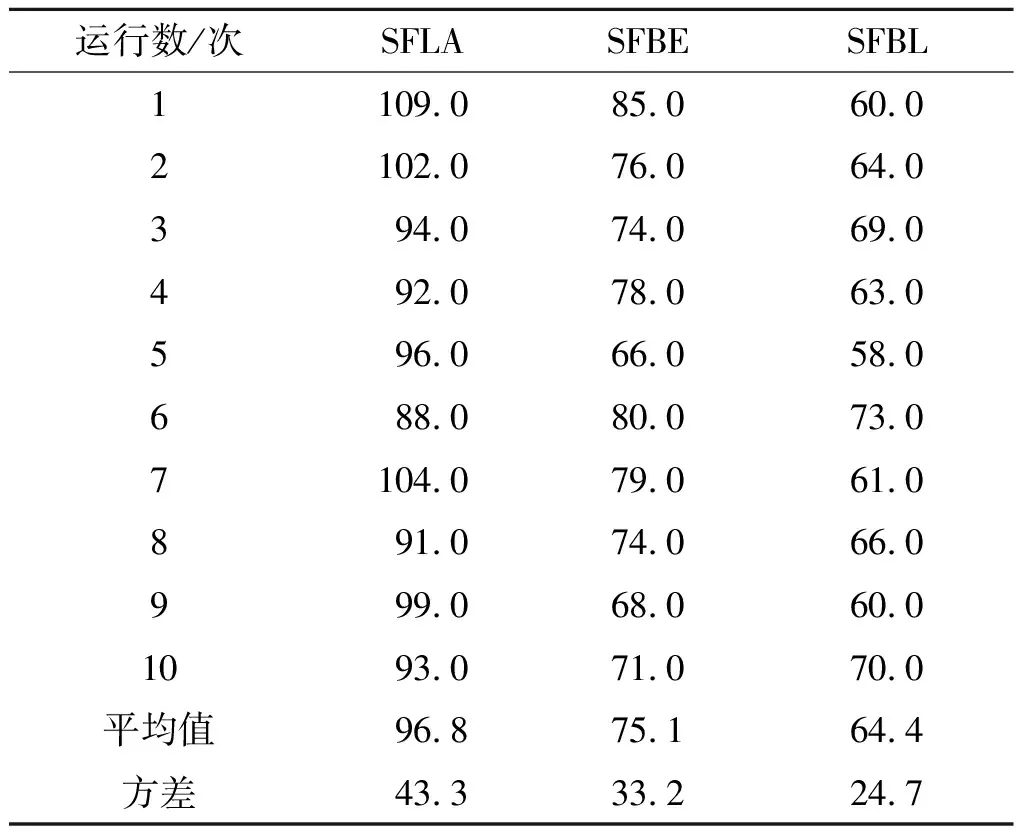
表2 SFLA，SFBE和SFBL的收敛代数Table 2 Convergence times of SFLA，SFBE and SFBL

由表2可以看出：SFLA算法平均迭代次数最多，为96.8；其次是SFBE算法，平均迭代次数为75.1；最后是SFBL算法，平均迭代次数最少为64.4。说明SFBL算法收敛速度最快，效率更高，在求解更大规模的样例和模型时具有更大优势；同时，从迭代次数的方差来看，SFBL的方差最小为24.7，说明SFBL算法相比于另外两个算法更稳定。

3.2.2 目标函数分析

为了更清楚地比较3 个算法在求解LRP模型上的最终效果，把3 个算法目标函数的碳排放随着迭代次数的曲线图放在一起比较，见图7。由图7可知：SFBL算法的末端值最低，碳排放为165.353 kg，因此SFBL算法最终的解质量最优，说明SFBL算法更有效，能够避免早熟现象；从3 个算法的曲线来看，前期SFBL算法下降趋势最明显，其次是SFBE算法，最后是SFLA算法，说明了SFBL收敛速度最快。

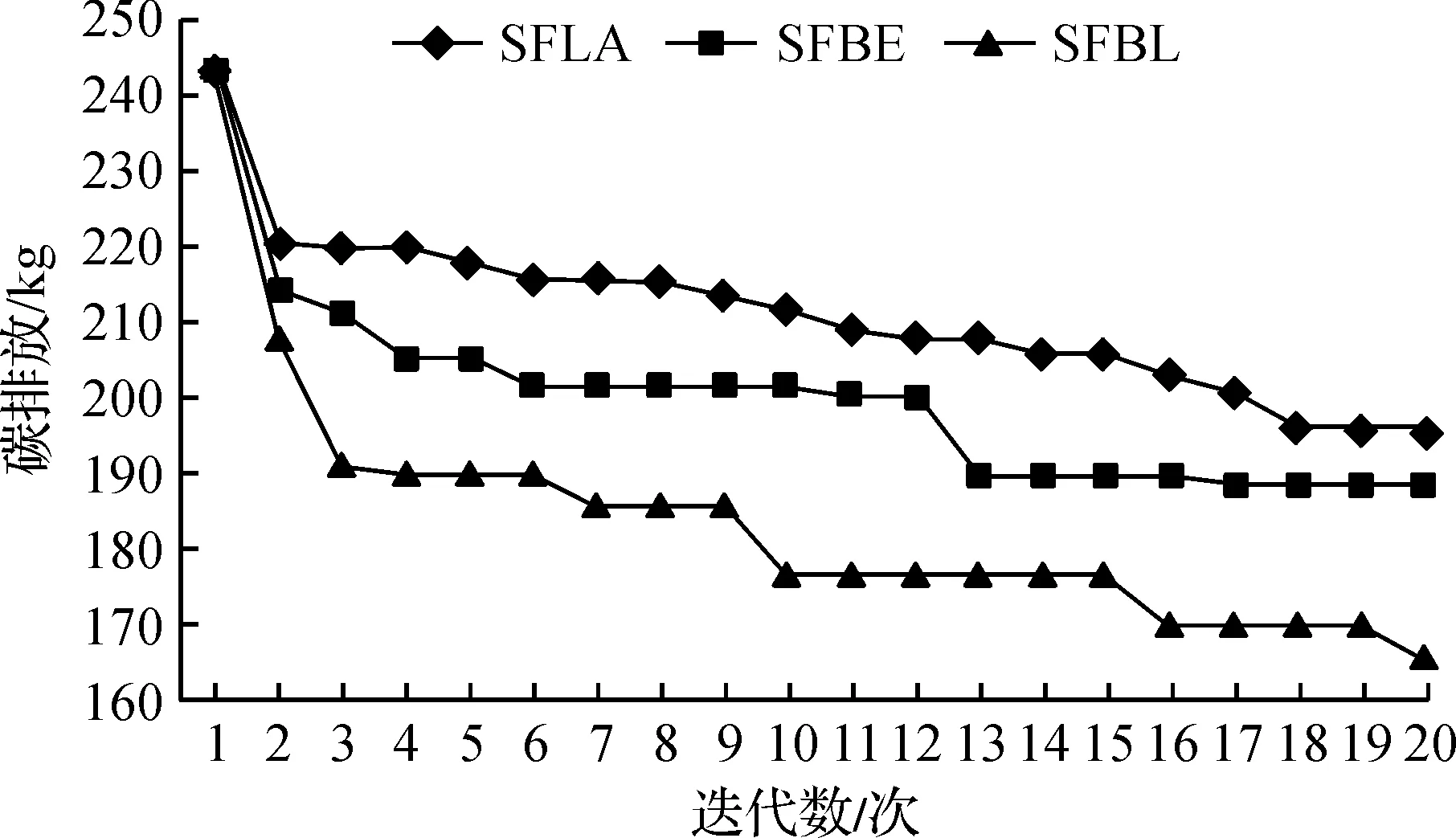
图7 目标函数收敛情况比较Fig.7 Comparison of objective function convergence

为了解给予蛙跳算法中底层启发式算子对解质量的影响情况，运行10 次，统计10 个底层启发式算子的平均改进率，即该算子对解的质量是否起到提升效果，如图8所示。

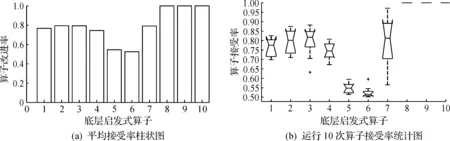
图8 算子的平均接受率Fig.8 Average acceptance rate of LLH

由图8可以看出：10个底层启发式算子的平均改进率都超过了0.5，其中局部搜索算子LLH8，LLH9，LLH10的改进率为1，这是由算子本身的性质所决定的，因为算子本身只接受改进解，其余算子从高到低分别为LLH2，LLH3，LLH7，LLH1，LLH4，LLH5，LLH6，相对而言，由于LLH5和LLH6是跟配送中心有关的算子，因此改进率比较低。总体而言，10 个底层启发式算子都有大概率能改进解的质量，证明了算子构建的有效性。然后，对于低碳LRP问题，3 种算法给出的最优解分别为：SFLA算法195.331 kg，SFBE算法188.476 kg，SFBL算法165.353 kg。这3 个解对应的路线如表3所示。

最后，为了验证3 个算法的通用性，将3 个算法分别用在3种不同规模的12 个测试样例上进行实验，分别为20 个客户点，50 个客户点和100 个客户点，配送中心均为5 个，每个规模4 个测试用例，目标函数改为所有车辆行驶距离的总和。

表3 最优路线Table 3 Optimal routes

3 个方案，12 个样例的结果如表4所示，加粗表示为该样例在3 个方案中最好的结果。从运行时间方面来讲，因为是毫秒级，3 个算法的复杂度一样，所以运行时间差距不大，总体而言SFBL方案运行时间最少。从目标函数而言，SFBL方案所获得的解质量最高，其次是SFBE，最后是SFLA。总体而言，问题规模越大，SFBL算法能获得最优解的概率就越高。

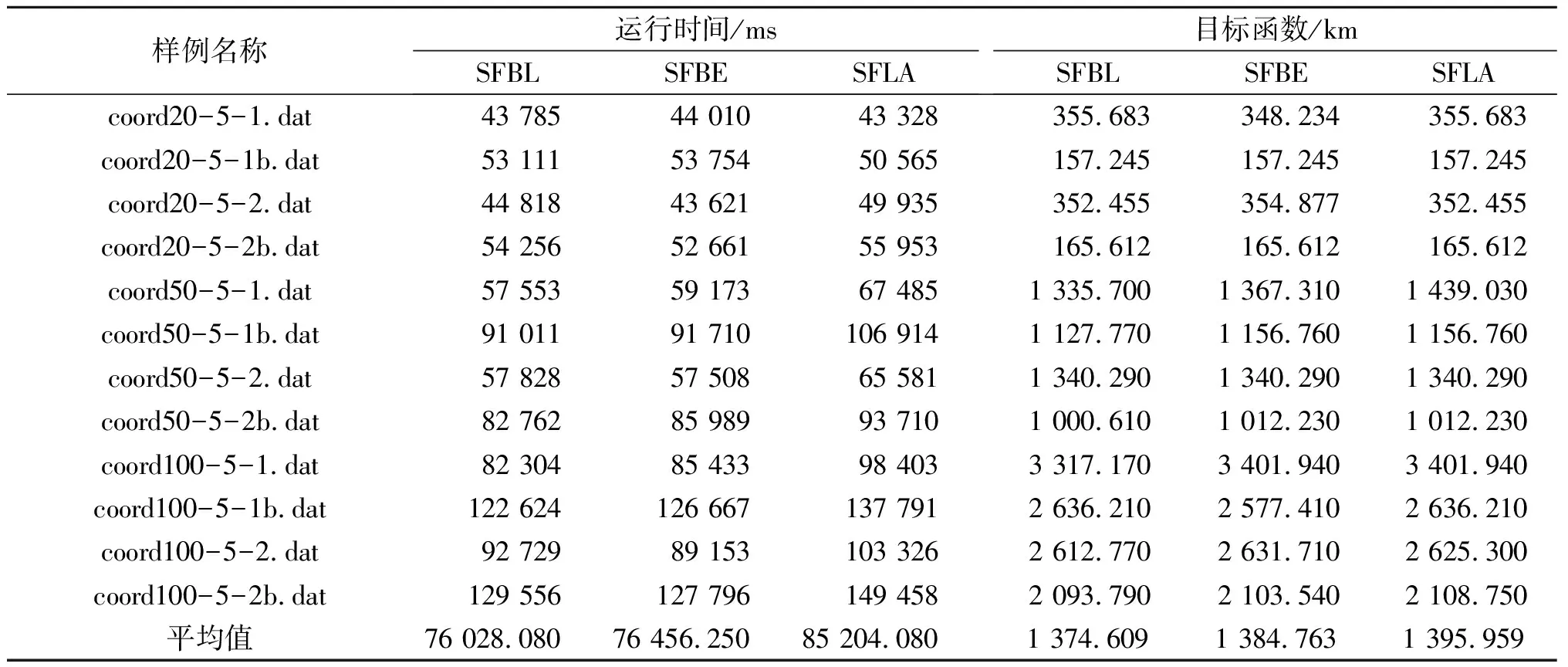
表4 SFLA,SFBE和SFBL对比Table 4 Comparison of SFLA, SFBE and SFBL

由此可见：无论是从算法的收敛代数、收敛速度、稳定性和通用性，还是从最优解来看，基于最长公共子序列的相似度计算方式(SFBL算法)都比其他两个算法要好。

4 结 论

针对低碳LRP模型，构建了和问题相关的底层启发式算子，使用蛙跳算法作为选取底层启发算子的高层策略，并提出了基于最长公共子序列的青蛙个体相似度计算方式，最后，将笔者提出的相似度算法与之前的相似度算法还有最原始的蛙跳算法比较，进行仿真实验。实验结果证明了算子构建的有效性，也表明基于最长公共子序列的相似度计算方法(SFBL算法)在求解低碳LRP能够在获得更好解的同时，具有更快的收敛性和稳定性，对跨问题领域求解效果也比较好。