车辆器材仓库收发能力评估

谢鑫鹏，张大鹏，任 聪，高 瑞

（陆军军事交通学院，天津 300161）

1 引言

我军后方车辆器材仓库主要用于保障部队执行应急机动、战备演练、抢险救灾等重大任务。它是战略、战役后方进行车辆器材储备和供应的基地，是军队后勤保障力量的重要组成部分，是军队作战运输的依托。其车辆器材收发能力的大小，不仅直接影响到后勤运输方案制定与修改，而且还影响到军队战斗力的体现和国家的军事能力。

同时，未来战争将会是高技术条件下的局部战争，战争爆发突然，战略纵深大，消耗的车辆器材多，这将会使得车辆器材物资的保障时间变短，任务加重[1]。后方车辆器材仓库作为交通运输基础的重要后勤保障基地，需准确评估其车辆器材收发能力的大小，以此查找出后方车辆器材仓库存在的缺陷与问题，改善收发的组织管理方式，提高仓库的保障能力，使其达到未来战争对车辆器材保障快速、准确、及时、高效的要求。

2 离散事件系统概述

车辆器材收发系统是一个高度开放的离散事件系统，其结构关系复杂，影响因素较多，且相当一部分是随机动态的。本文将采用离散事件理论，利用数学建模方法对车辆器材收发系统建立作业能力评估模型。

离散事件系统是指其活动和状态变化仅发生在离散的时间点上，同时状态的变化与事件紧密联系的系统。物流系统可以被认为是一个复杂的离散事件系统，其特点是它的状态变量只是在离散时间点上发生变化，并且这些离散时间点一般也是不确定的，具有随机性。同时，系统的状态变化也会具有随机性，同一种内部状态由不同事件或原因触发，可以向多种状态转变[2]。另一方面，系统内部状态只在离散时间点上发生变化，且状态在一段时间内保持不变。在这类系统中，对系统行为进程起决定作用的是一批离散事件，而不是连续变量。图1为后方车辆器材仓库发出车辆器材流程图。

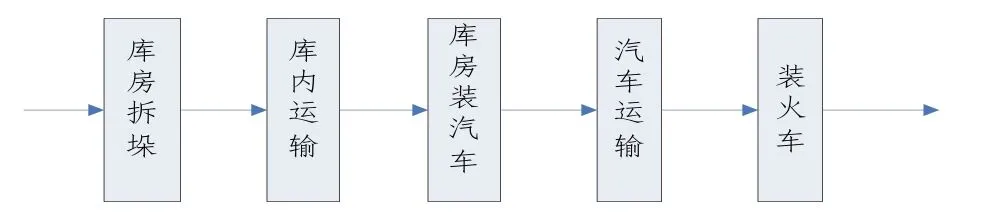
图1 后方车辆器材仓库发出车辆器材流程图

如图1所示，“库房拆垛”活动的开始会引起各种搬运装卸机械工作，而搬运装卸机械工作又会改变车辆器材、库存的状态，“库房拆垛”事件还会改变库房站台的状态，激发装汽车活动的开始，依次激发后面的汽车运输、装火车等活动。事件持续传递和变换，演绎着仓库收发系统的动态行为。由此可见，后方车辆器材仓库收发作业系统是典型离散事件动态系统。

3 离散事件系统研究方法

离散事件系统研究常用的方法有系统仿真和解析法（优化法、排队论）。

3.1 系统仿真方法

系统仿真是利用数学公式、逻辑表达式、图表、坐标等抽象概念来表示实际物流系统的内部状态和输入输出关系，以便通过计算机对模型进行试验。系统仿真既能反映系统的物理特征和逻辑特征，也能表达系统的静态性质和动态性质，有利于对系统进行分析。但系统仿真要求使用人员的编程能力较强，对仿真软件需有很深的认识，且建模时间长，模型调试困难，模型的通用性、适应性和可借鉴性较差，所以一般不采取这种方法。

3.2 解析法

解析法主要采用最优化方法和排队论方法。最优化方法是运用线性规划、整数规划、非线性规划等数学方法来描述物流系统的数量关系，以求得最优决策。其主要用于物流方面，即约束规定一个可行解的区域，求目标函数为最低成本或最大完工时间的最优解。

排队论，又称随机服务系统论。它是研究拥挤现象和排队现象的学科。它能研究系统的形态、运行规律以及最优设计与最优控制，广泛用于离散系统的建模。且建立的排队网络模型，易于从概率统计的角度分析并优化离散事件的过程及性能，具有解析形式的解，能得到定量的结果[3]。因此，本文主要采用排队论方法进行研究。

4 相关基础知识及符号假设

4.1 基本概念

排队是指需要得到某种服务的对象加入等待的队列。需要服务的对象泛称为顾客，从事服务的设施或人等泛称为服务台。顾客与服务台构成一个系统，称为服务系统。在一个服务系统中，若某时刻顾客的数目超过服务台的数目，就会产生排队现象，为排队现象的服务系统称为排队系统。排队系统可抽象描述如图2所示。

图2 排队系统组成

在车辆器材收发作业过程中，库房站台就是一个装载服务台，存在排队现象：当运输车辆开至库房站台，仅当库房站台有充足车辆器材且装卸服务台空闲、有空的搬运设备时，才能进行车辆器材的装载作业[4]。

4.2 组成和特征

一般，排队系统都有三个基本组成部分：输入过程、排队规则、服务机构。

输入过程：描述顾客来源是按怎样的规律抵达排队系统。首先包括顾客源总体数是有限还是无限；其次应说明顾客到达的方式，是单个到达还是成批到达；最后应说明顾客相继到达的时间间隔的概率分布。

排队规则：指服务系统是否允许排队，顾客是否愿意排队。服务顺序是什么，一般有先到先服务、后到先服务、随机服务、有优先权的服务等。

服务机构：指服务台的数目和服务时间服从怎样的概率分布。

4.3 常用符号假设

下面给出能反映排队系统的几个主要性能指标：

Ls：平均队长，即稳态系统任一时刻的所有顾客数的期望值；

Lq：平均等待队长，即稳态系统任一时刻的等待服务的顾客数的期望值；

Ws：平均逗留时间，即（在任意时刻）进入稳态系统的顾客逗留时间的期望值；

Wq：平均等待时间，即（在任意时刻）进入稳态系统的顾客等待时间的期望值。

其他常用指标有：

s：系统中并联服务台的数目；

λ：平均到达时间；

1/λ：平均到达间隔；

μ：平均服务率；

1/μ：平均服务时间；

ρ：服务强度，即每个服务台单位时间内的平均服务时间，一般有

N：系统中的顾客数。

5 车辆器材收发系统模型建立及求解

5.1 模型的假设

假设：车辆器材发出作业的车辆数为m辆，采用一个库房站台装卸作业，站台的服务时间为t装，汽车满载运输、火车站台卸车辆器材、汽车空返的时间分别为t重运、t空运、t卸。

由车辆器材收发流程过程中可知，在车辆器材收发过程中，从库房站台到火车站台卸载主要包括四部分：库房站台装车、汽车满载运输、火车站台卸车辆器材、汽车空返[5]。我们将这个装运卸载的过程看成一个排队服务系统，此系统共分为四级，如图3所示。

图3 车辆器材收发流程四级排队服务系统

5.2 模型的分析

首先，第Ⅰ级为装车服务系统。运送车辆器材的汽车首先到达洞库站台的装载服务台，此时当且仅当洞库装载服务台空闲且有足够车辆器材量搬运给汽车时，才能进行车辆器材的装载作业。这里先考虑只有1个服务台（装卸组）的情况，服务时间平均为t装。

其次，第Ⅱ级为汽车满载运行服务系统。此系统有n个服务台，可以保证所有汽车能同时进入重车运行服务系统进行服务（即驶往火车站台），不需等待。假定各服务时间（即满载运行时间）均为t重运。

再次，第Ⅲ级为卸车服务系统。通常在卸车服务台（火车站台）也会存在排队现象，为了研究方便，这里把卸载时间和等待卸车时间统一为卸车服务时间。假设卸车服务时间均值为t卸。

接着，第Ⅳ级为空车返回服务系统。它的特征和第Ⅱ级服务系统一样，不同的是汽车空车返回速度较快，这里还把空车到达后，把装车前的入换时间归并到空车运行时间。假定各系统的服务时间均为t空运。

最终，第Ⅳ级服务完毕，准备转入第Ⅰ级服务系统接受服务。

由上分析可知，车辆器材收发系统即可看作为m个顾客（m辆汽车）依次接受四级服务，接受了第Ⅳ级服务后，就返回到第Ⅰ级前等待队伍的末尾，如此不断地循环运行，形成一个顾客源有限的闭合式四级串联循环排队系统，此系统可简化为图4所示。

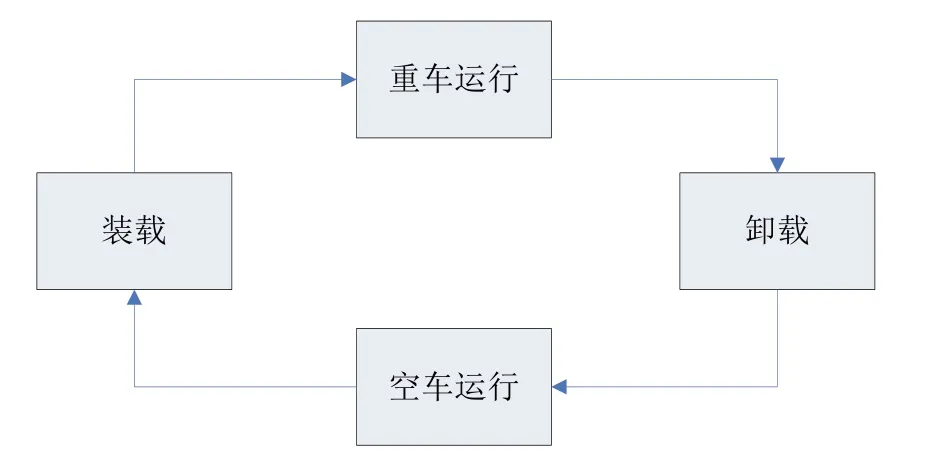
图4 车辆器材收发系统简化图

再把汽车满载运输、火车站台卸车辆器材、汽车空返三部分称之为车辆器材卸载系统。库房站台装车部分称为装载系统。由此可以建立出服务台数为1，顾客数为m的有限循环排队模型：M/M/1，如图5所示。整个过程近似于“生灭过程”。

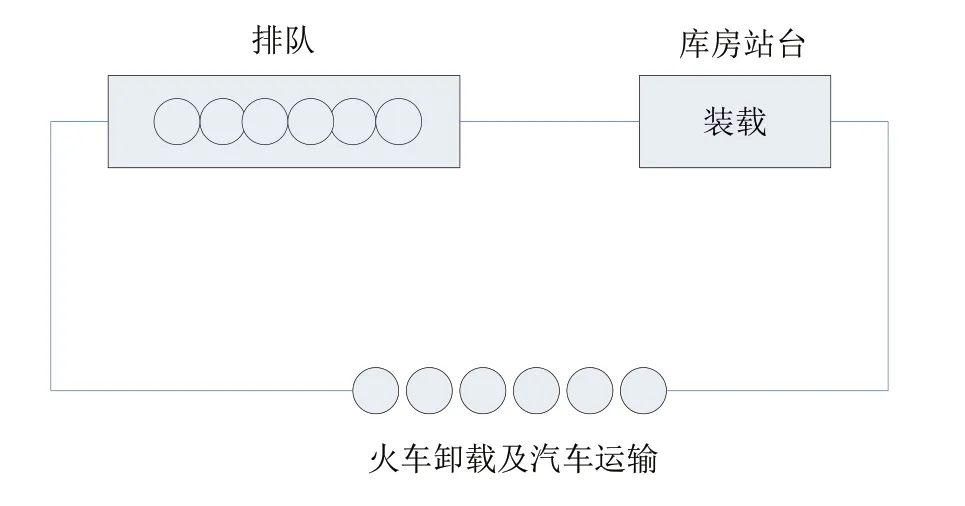
图5 车辆器材收发的有限循环排队模型

对该模型，我们还做以下假设：

（1）假设车辆器材发出作业的汽车按泊松流到达库房站台，站台的服务时间服从指数分布；

（2）假设在运输过程中，道路宽敞，汽车在路上不会发生堵车现象，且未受天气、道路条件等因素的影响，满载运输速度为35km/h，空车返回速度为60km/h；

（3）由于部队服务的特殊性，一天的工作时间可以稍长，假定一天工作时间为9h；

（4）车辆每次装载量相同，未超过其额定装载质量；

（5）车辆器材收发时，由于提前拆垛，能使车辆到达就立刻装车，无需等待。物资由库房发出，依次经过各服务台到达火车站台卸载，直到最后一辆汽车卸载点清完毕后，作业结束。

通过上述分析，我们建立了从库房站台到火车站台的有限循环排队模型。类似的，在库房拆垛到运输至库房站台这一过程，也可建立以牵引车为顾客的循环排队模型。

5.3 模型的求解

由以上数据可得，汽车的平均运输周期为：T周=t装+t重运+t空运+t卸；单位时间内，汽车的平均到达率为：λ=1/T周；站台的平均服务时间为：μ=1/t装。系统状态变化的生、灭过程如图6所示。

图6 系统状态变化的生灭图

其中，0、1、2、…、m-1、m表示在第Ⅰ级服务系统装载的汽车数量。

根据生灭规则，可得系统的极限概率为：

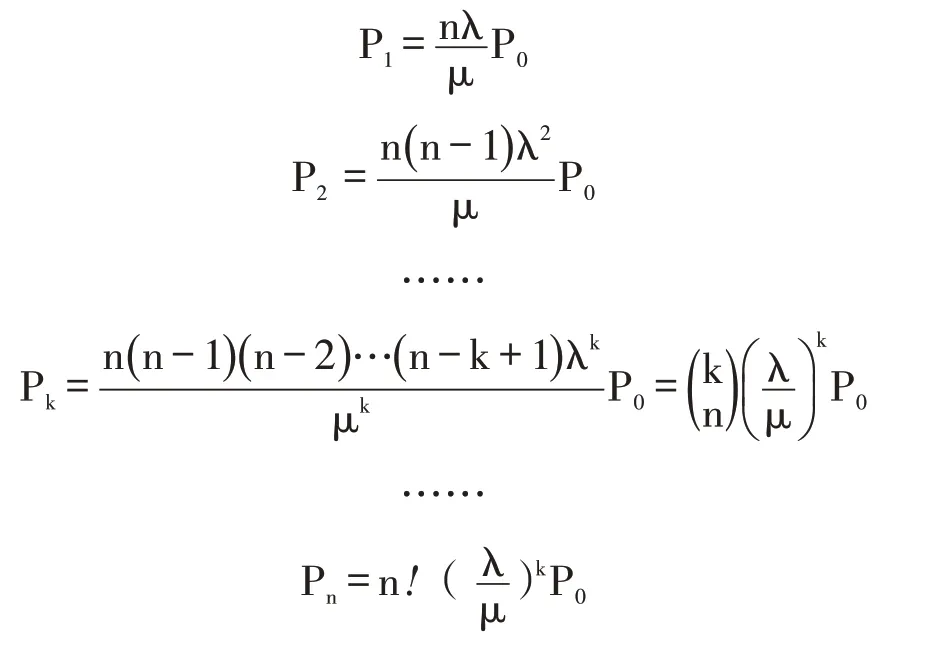
其中P0+P1+…Pk+Pn=1。

P0表示在第Ⅰ级服务系统装载的汽车数量为0，即所有汽车都在运行，库房站台处有0 辆汽车的概率（即库房空闲时的概率）。

根据以上公式，结合排队论知识，我们得到车辆器材仓库的收发系统其他指标的表达式：

6 小结

本文通过研究得到了如下结论：影响后方车辆器材仓库收发能力的因素有很多，它包括人员组织协调能力、人员与机械设备的数量、人员与机械的作用效率、库房设施、道路条件、离铁路专线（站台）距离等因素；同时，为了提高车辆器材的收发能力，可以通过加强人员业务训练、改善库房周边环境、采取集装箱等科学管理措施，合理配置人员与车辆，以此提高库房拆垛效率和装载效率，以达到增加收发能力的目的。