钛合金超声检测的信号特征与处理方法

(中国船舶重工集团公司第七二五研究所, 洛阳 471000)

钛合金材料具有比强度高、耐蚀性好等特性，但材料成本高、焊接与加工难度大，过去只用于制作精密结构件或特殊结构件。近些年材料成型与加工技术的飞速发展,为钛合金的大范围应用提供了技术支撑，目前钛合金已成为船舶、航空领域的关键材料。大规格、复杂结构焊接成为当前钛合金产品发展的重要趋势，由此带来的钛合金材料的无损检测问题也亟待解决。

在兼顾适用性、经济性和直观性的条件下，超声检测是多类钛合金构件检测的优先选择，但其相关标准多建立在参照钢制结构的基础上，在大厚度构件检测、微小缺陷检测时遇到了挑战。根据经验，钛合金超声检测时会存在杂波干扰，且在大厚度检测或高灵敏度检测时干扰信号尤为强烈，甚至会完全湮没缺陷信号。材料微观组织、被检构件结构、检测系统等均是引起杂波的重要因素，对此，通常采用优化物理结构或信号处理技术来减少干扰，如采用聚焦探头、对信号降噪滤波等，但仅在特定条件下的应用效果较好[1]。为解决上述问题，笔者重点探讨了超声检测信号的特征与缺陷识别方法，在结合钛合金微观组织特点探讨其声学性能的基础上，分析了其信号特征并提取特征参数，建立了非线性分类模型，通过样本训练实现了杂波与缺陷信号的分类，为大规格、高灵敏度超声检测提供了一种新思路。

1 信号特征分析

1.1 钛合金声学性能

钛合金组织一般分为等轴、双态、网篮与魏氏等4类，其组织由α相、β相构成，α相和β相的比例与形态不仅决定了材料的性能，且对超声波的声学性能有直接影响。超声波声速与衰减系数是超声检测中必须关注的材料声学特性参数，亦是保证缺陷定位与定量精度的基础。选择TC4钛合金为研究对象，制备等轴、双态、网篮与魏氏组织试块各1块，采用水浸超声C扫描进行试验，测试各试块的超声波信号并计算声速与衰减系数，图1为水浸超声设备外观及试验现场图片。

图1 水浸超声设备外观与试验现场图片

试块规格(长×宽×厚)为300 mm×90 mm×40 mm，加工精度为±0.02 mm，3个尺方寸向分别定义为x,y和z，分别对这3个尺寸方向进行试验。试验采用频率为5 MHz的平面探头，水层厚度大于近场区，采样率为200 MHz，采用栅格扫查分别获取3个尺寸方向的超声信号，每个方向50个采样点。利用固定厚度下的绝对时间差、幅值衰减量，分别计算纵波声速与衰减系数，为减小误差，以50个采样点的计算平均值为最终结果，表1和图2为最终测试结果。

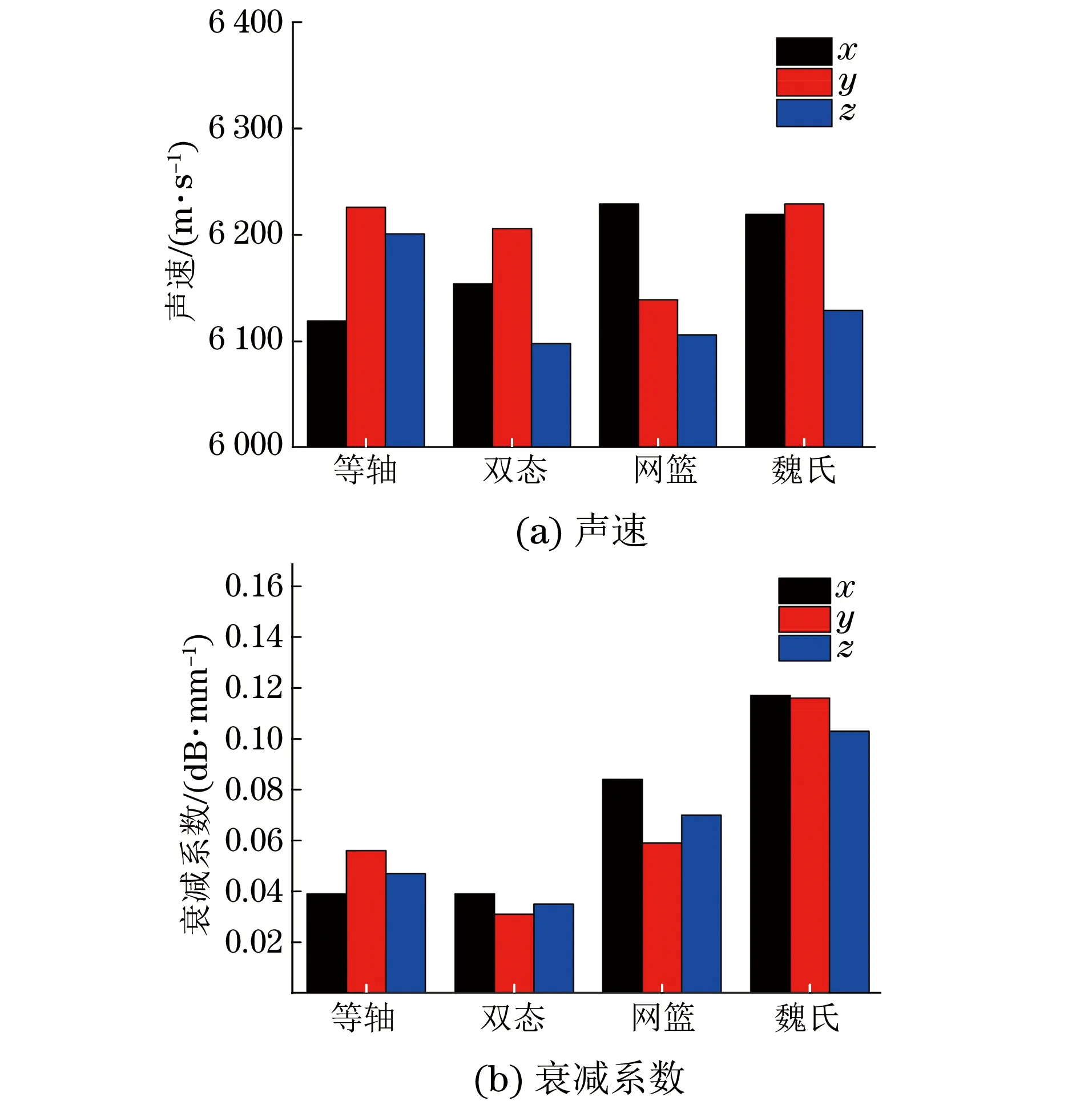
图2 不同组织的试块在各方向的声速与衰减系数

根据试验，钛合金纵波声速与微观组织并不存在绝对的对应关系，声速范围为6 098～6 226 m·s-1，

表1 声速与衰减系数

变化区间相对较小且呈现微弱的各向异性，材料组织不均匀引起的声速变化对缺陷定位的影响很小。不同组织间的超声纵波衰减系数则差别较大，网篮与魏氏组织的衰减系数明显大于等轴与双态组织的，且均呈现明显的各向异性，实际检测时能量衰减、缺陷定量应关注这一因素。

1.2 超声信号特征

钛合金超声检测中的干扰杂波主要源于材料内的晶粒散射，尤其在采用高频率、高灵敏度检测时尤为显著。除受被检材料本身组织的影响外，杂波信号亦与检测频率、检测厚度等其他参数存在一定关系，图3(a)为等径平底孔信号在不同深度下的信噪比变化，图3(b)为同深度，不同脉冲电压下的信噪比变化。由图3可见：检测深度增大时，平底孔信号信噪比总体呈下降趋势，平面探头的信噪比在近场区内会有波动，聚焦探头的信噪比在焦点附近最高，且随深度增大迅速减小；脉冲电压幅值增大时，虽然超声波能量增强，但散射杂波随之增强，信噪比并无明显变化。

图3 平底孔深度、脉冲电压幅值变化时，信噪比的变化

图4 极限检测厚度下，φ0.8 mm平底孔的时域信号 与频域信号

实际检测中，通常采用降低频率、分区扫查、选择聚焦探头等方式来提高信噪比，但却同时存在绝对灵敏度降低、聚焦深度范围过小等弊端，很难从根本上解决信噪比低的问题。信号的信噪比越高越有利于缺陷的识别与分析，信噪比低于12 dB时，散射杂波信号将与缺陷信号发生叠加，而可能掩盖小缺陷信号并增大缺陷定量的不准确性。以钛合金锻件为例，将基准灵敏度设置为φ0.8 mm平底孔时极限检测厚度约100 mm，此时平底孔对应的时域与频域信号见图4，杂波信号与平底孔信号的频谱均集中在探头中心频率(5 MHz)附近，常用的带通、带阻等数字滤波法对提高信噪比基本无明显效果。

钛合金超声检测信号中含有较高的散射杂波成分，杂波水平高低与被检对象、检测参数密切相关，由此造成的信噪比偏低是制约大厚度产品检测的关键因素。虽然由组织晶粒造成的超声波复杂反射、衍射等信号经过多次叠加才传输到超声换能器，但其本质上与缺陷反射波均属于声波的线性弹性响应信号，故在时域上无明显区别，在简单的频域变换中也很难识别。

2 缺陷信号处理

2.1 特征参数提取

特征参数是信号评定的依据，在复杂信号识别中,特征参数的选择尤为重要。而在杂波干扰严重的钛合金超声检测信号中，时域中的幅值、波宽等参数已不适用于表征缺陷信息，故文章采用小波分析与能量熵结合的方式提取数据段的特征参数。小波分析的窗函数可变化，具有多分辨率分析的特点，特别适合于弱突变信号的处理，利用该特点对缺陷信号进行分解能获得丰富的缺陷信号细节特征。小波能量熵是在信息熵的基础上演变而来的，在非平稳信号处理中具有良好的应用效果，常用于描述系统复杂程度或表征突变信号[3]。信号小波分解后分布于N个频带，将各个频带的能量定义为E1，E2，…，EN，且E为各频带能量之和，则小波能量熵的计算见公式(1)。

(1)

在超声检测完整信号段中，很可能存在因缺陷深度较小而产生的多次缺陷反射波，若将整段信号一次性分解，则会增加信号识别的不确定性。缺陷响应的信号长度基本与激励脉冲宽度接近，信号周期数一般为3～5个，探头频率越高,缺陷响应信号长度越短。在上述特点的基础上，以响应信号时间长度为参考，设定深度定尺区间，采用窗口滑动实现对完整信号的处理，区间长度即为缺陷深度分辨力。选择正交小波基db4对区间信号进行3层小波包分解，并计算第3层8个频带的能量熵，图5所示为杂波信号与缺陷信号的各频带能量熵。

图5 杂波与缺陷信号的各频带能量熵值

虽然图5中的杂波信号与缺陷信号的能量熵值主要体现在前4个频带中，但杂波信号的后4个频带中依然有明显的幅度，缺陷信号与杂波信号的各频带能量熵值呈现很大的差异性，不能以某一频段的熵值差异区分杂波信号与缺陷信号。故应选择8个频带的能量熵值a={WE1，WE2，WE3，WE4，WE5，WE6，WE7，WE8}作为信号特征向量，同时结合分类算法输入特征向量识别缺陷信号。

2.2 缺陷识别

在将分段信号分解为8个特征参数的基础上，缺陷的评判已转换为多参数模式识别问题，目前常用的方法主要有支持向量机(SVM)和神经网络。支持向量机基于统计学习理论，通过建立一个分类超平面,作为决策平面近似实现结构风险最小化;而神经网络采用模拟大脑神经元的方式组成非线性、自适应信息处理系统。SVM本质上为一个二分类器，利用核函数代替高维空间映射解决非线性问题，理论完善且通用性好，但在多分类和大规模样本训练时存在困难[4]。神经网络的神经元之间通过权系数相连接，信息分布式存储于权系数中，具有容错性高、抗干扰能力强的特点[5]。为达到满意的信号处理效果，分别采用SVM、LVQ与BP神经网络识别信号，对比缺陷识别的准确率。

(1) 建立模型

SVM的分类性能与核函数的选择密切相关，常用的核函数包括线性核函数、d阶多项式内积核函数、径向基核函数等，目前尚无系统的选择标准，参考其他SVM分类应用研究，选择径向基函数作为核函数。经小波包分解后的频带能量熵值即为样本输入向量，由于能量熵值均分布于0～1区间内，故不再对样本数据进行归一化预处理。LVQ神经网络由输入层、隐含层和输出层组成，输入层与隐含层完全连接，隐含层与输出层则部分连接，网络结构简单，通过计算输入向量与竞争层间距离实现分类。BP神经网络属于多层前馈神经网络，具有信号前向传递、误差反向传播的特点，创建的网络为3层，结构为8-25-2。上述3种模型均在MATLAB软件环境下建立。

(2) 训练模型

训练数据源于钛合金棒材、锻件与板材的水浸超声检测数据，既包括人工缺陷又含有夹杂、开裂等缺陷。为模拟大厚度检测信噪比低的状态，部分试件试验时采用了较高的频率，信噪比均在6 dB以下。按2 mm深度区间截取的试验数据共120组，缺陷数据与杂波数据各60组，图6所示为各组数据小波包3层分解后的能量熵值。图6中前60组为缺陷样本、后60组为杂波样本，各频段的杂波与缺陷能量熵值都存在交叉重复情况，无法根据单频段熵值进行直接区分。将缺陷与杂波数据等分为两部分，一部分用于训练模型，另一部分用于测试分类效果。

(3) 测试模型

对LVQ和BP神经网络分别训练1 000步，其中LVQ网络误差收敛速度很快，训练步数达到27步后均方误差基本在0.1附近波动，而BP网络训练步数越多均方误差越小，训练步数达到62步时均方误差已达到0.000 1。表2为模型训练后的分类测试结果，各个模型的总体识别准确率均达到了80%，神经网络分类模型优于SVM模型，BP神经网络分类准确率最高。

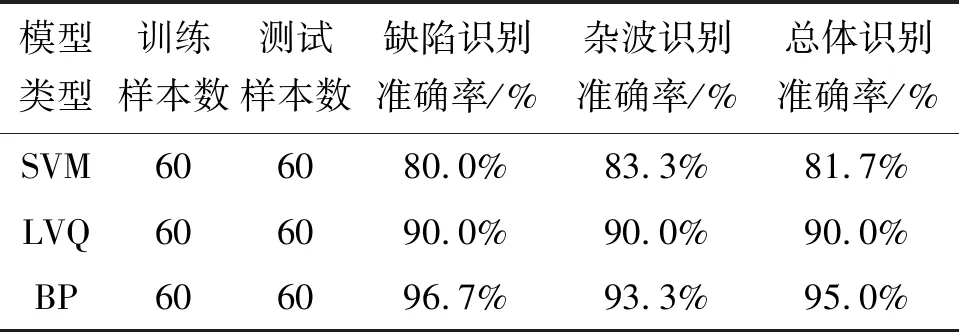
表2 实测模型分类准确率

3种非线性分类模型均表现出良好的分类效果，对于钛合金超声检测低信噪比的缺陷信号的最高识别率达到90%以上。受限于训练样本数量，各个模型并未达到最佳的训练效果，在增大样本数量的基础上，分类模型的准确性将进一步提高。虽然能通过优化SVM核函数的方式提高其分类准确性，但文章试验仅限于缺陷识别的层次，若考虑缺陷定量的多分类模式，则SVM可能不具有明显的优势，因此应用中应优先选择BP神经网络分类模型。

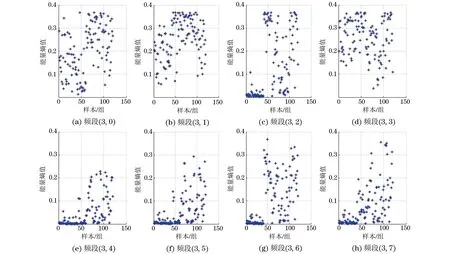
图6 样本数据小波包3层分解后的能量熵值

3 结语

钛合金材料的声学性能受微观组织变化的影响，声速变化区间较小，但衰减系数最大差异达到70%以上且呈现出各向异性，实际检测时应关注这一特征。超声检测信号杂波主要源于晶粒散射，大厚度或高灵敏度检测时，信噪比会严重下降而导致缺陷信号难以识别，杂波信号与缺陷信号的频域分布较为接近，常用的滤波方法效果并不明显。采用小波能量熵表征信号特征，结合SVM、LVQ与BP神经网络区分杂波与缺陷信号，识别准确率达到90%以上，为解决杂波干扰问题提供了一种方法，但在缺陷定量的方向上有待进一步研究。