基于拓展CBBA算法的在轨装配航天器任务分配技术研究

于晓强，郑红星

（哈尔滨工业大学，哈尔滨 150001）

1 引 言

在轨装配技术属于模块化航天器技术的重要组成部分［1］，是可以将受限制的大型空间结构等大质量、大体积的地面装备拆解后分批次地发射到空间中再进行装配的关键技术之一［2］。随着未来空间科学任务的日益复杂以及人工智能产业的蓬勃发展，对智能化、自主化空间在轨装配任务规划技术的需求也逐步提高［3-5］。目前的在轨装配任务不再局限于单个航天器独自安装，而需要多个航天器协同完成多类在轨装配任务，从而实现空间资源的高效利用［6］。面对不同种类的在轨装配任务（如零件运输任务、安装任务、维修任务等），不同任务之间会有一定的时间窗限制，如何统筹分配所有不同种类航天器资源，在最大化满足装配需求和资源充分利用的条件下，制定出最佳的航天器装配任务执行方案，是在轨装配领域中出现的亟待解决的新问题。

本文所研究的问题可描述为：针对大量在轨装配任务需求，在满足装配任务的类别约束及时间窗约束下，解决将各项任务分配给多个多种类航天器的在轨装配任务分配问题，即确定使用哪些航天器在哪段时间内按照什么顺序来执行哪些特定任务，以满足不同任务对不同种类机器人及各自完成时间的装配需求，最终实现在轨装配任务圆满完成、且综合效益最大的目标。任务描述如图1所示。

常见的任务分配算法主要包括基于合同网的市场拍卖方法、分布式马尔可夫决策方法和模型预测控制方法［7-10］。其中，基于合同网的拍卖算法面向动态任务的自主分配，并在过程中考虑智能体之间的信息交互和协商，是一种相对容易实现的分布式算法［11-13］。基于一致性的捆绑拍卖算法（Consensus-Based Bundle Algorithm，CBBA）是一种利用拍卖算法的多任务分配算法，允许智能体对每个任务进行竞价，然后开发一个共识算法来解决智能体之间的分配冲突［14-15］。本文提出了一种改进的CBBA算法，用于将具有协同任务约束的装配任务分配给具有不同能力的异构在轨装配航天器团队。

本文提出的改进算法包括以下两个方面：

（1）为体现在轨装配中运输、安装等任务的时间先后特性，为每个任务设置完成时间窗及完成任务所需时间。通过设计新的竞价函数，考虑运输及装配航天器运动速度及任务时间窗约束，保证所有任务在规定时间段内完成，并使整个航天器团队所花费的时间或路程代价最小。

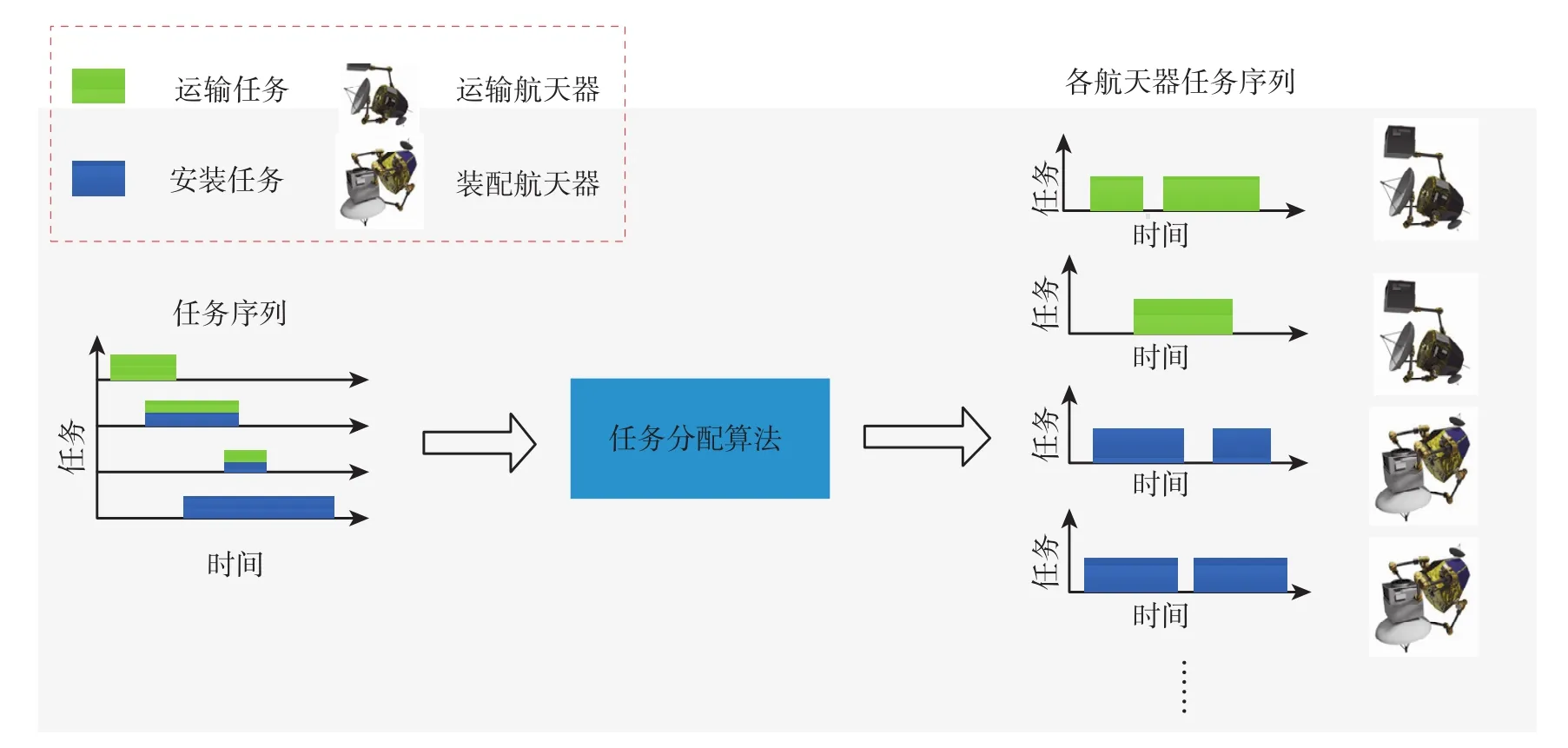
图1 在轨装配任务分配问题描述Fig.1 Description of on-orbit assembly task assignment problem

（2）考虑某些复杂运输/安装任务需要多个运输/安装航天器协同完成，这是原算法无法处理的情况。本文提出了一种新的一致性算法，更改了本地拍卖信息的储存方式，并提出了一种新的分配冲突解决规则，使算法可以处理多智能体任务分配问题。

最后，对本文提出的算法进行了仿真实验，证明了该算法能够在不增加额外计算时间情况下收敛到一个无冲突、可行的任务分配解决方案，可解决复杂多约束的在轨装配任务分配问题。

2 算法模型

2.1 CBBA算法原理

CBBA算法是一种分布式拍卖算法，为多智能体多任务分配问题提供了可靠的解决方案。CBBA算法在两个不同的阶段之间迭代进行，分别是拍卖包构建阶段和共识阶段，拍卖包构建阶段每个智能体按一定的顺序生成一个本地的任务包，共识阶段通过相邻智能体之间的通信及一致性算法解决分配冲突。

第一阶段：拍卖包构建阶段。每个智能体在本地构建一个任务包，其中包含它计划在分配过程中完成的所有任务，然后智能体不断地向包中添加任务并进行合理排序，直到达到它所能完成的任务数量上限。每个智能体i任务包中含有两个任务相关向量：bi和pi。其中bi按添加进包的先后进行排序，而pi按智能体计划完成任务的先后进行排序。表示智能体i按p中的任务序列执行任i务得到的总奖励，当包内插入了新的任务j时，表示将任务j插入到任务路径pi的第n个位置后得到的总奖励。cij［bi］表示由于添加任务j到任务包而导致的得分增长量。

每个智能体在当前路径pi中的所有可能位置插入新任务j，从而确定使cij［bi］最大的位置n。然后依次添加所有智能体可完成的任务至任务包内，从而确定出最大化任务奖励的完成路径pi。

每个智能体在构建完成自己的任务包后，需要构建包含竞标信息的量：中标价格列表yi、中标智能体列表zi、更新时间si。yi表示每个任务的当前出价中出价最高的价格，zi表示出价最高的智能体，zij=k表示智能体i认为任务j被分配给智能体k。智能体不仅需要知道它选择的任务是否高于最高出价，还要知道每个任务的分配对象。因此，需要更复杂的冲突解决规则来解决多智能体间的分配冲突，实现更好的分配。

第二阶段：共识阶段。CBBA算法的共识阶段是避免太多智能体分配到相同的任务。当智能体i收到来自另一个智能体k的消息时，yi、zi和si用于产生无冲突的任务分配细节。智能体i可以对任务j采取三种可能的行动：（1）更新：当yij＜ykj时，；（2）保留：当yij＞ykj时，；（3）重置：当路径pi中已经有其它变动，yij=0，zijij=∅。

如果以上规则更改了智能体的出价列表，每个智能体将检查更新或重置的任务是否在其任务包中，如果是，则在任务包内删除该任务。因为删除该任务会改变所有后续任务的得分，所以也需要删除在bin之后添加到捆绑包中的所有任务，对应的中标价格列表yi以及中标智能体列表zi都会被重置，即：如此依次解决每个任务的分配冲突，然后算法返回到第一阶段并重新添加新任务。算法会一直迭代这两个阶段，直到它们收敛到一个无冲突的解决方案。

2.2 考虑时间约束的竞价函数

考虑在轨装配过程中运输、安装等各子任务的时间先后，需要为每个子任务设置任务时间窗约束。本文设计了一种考虑任务复杂时间约束的竞价函数，考虑每个任务的时间约束，保证所有任务在其规定时间段内完成，并使整个航天器团队所花费的时间及路程代价最小。本文首先定义了时间分数项sj(t)以及时间窗uj(t)如下：

时间分数项sj(t)：表示航天器在时间t到达任务时从任务j获得的奖励，是基于任务的奖励值Rj和任务时间惩罚及距离惩罚的函数。

其中，（t-tjstart）是任务开始时间和航天器到达任务时间之间的差异，而λj是惩罚航天器迟到的折扣参数，Pdistance是惩罚航天器按路径p从上一任务到任务j所花费的路程项。

时间窗uj(t)：任务的有效时间窗口表示允许航天器执行任务的时间。对于任务j，此窗口定义为：

定义航天器对任务j的竞价函数cj(tij)为：

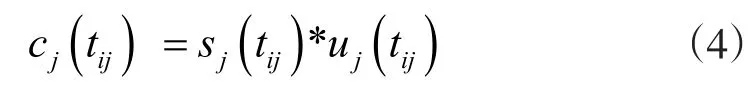
tij是其到达任务j位置的时间，是航天器在到达任务j之前所采取的路径p的函数。给定一个路径pi，和一组对于路径中所有任务k（k ∈pi）对应的最佳时间，对于每个任务j∉ p，执行任i务j的最佳时间定义为：

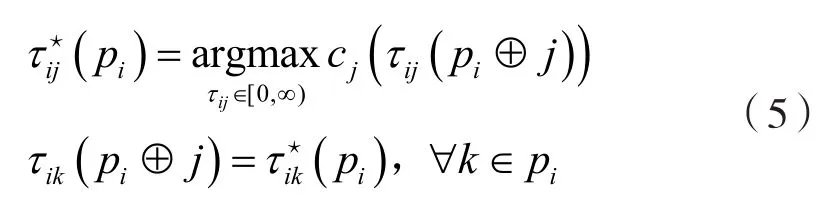
其中⊕表示将任务j插入路径pi而不改变pi中已有任务的顺序。上式约束为，将新任务j插入路径pi不能影响路径中已有任务的当前到达时间。通过将j插入最佳位置来更新路径。然后将任务j的最佳时间和得分保存为：和。

2.3 扩展一致性算法

考虑大型空间结构中某些复杂运输/安装任务需要多个运输/安装航天器协同完成，这是原算法无法处理的情况。本文据此提出了一种新的一致性算法，更改了本地拍卖信息的储存方式，并针对多智能体任务分配冲突提出了一种新的分配冲突解决规则。在算法的拍卖包构造阶段，每个航天器的任务包bi和路径pi的构造方法与原来的CBBA算法相同。在算法的分配冲突解决阶段，航天器接收来自附近航天器的所有任务分配信息的数据，然后使用一致性算法协调所有任务的分配冲突，下面对两部分内容分别进行详细描述。

2.3.1 航天器的信息矩阵构造

首先需要确定一致性算法所需的数据。当开始使用CBBA算法时，任务及航天器信息存储在航天器本地。每个航天器存储两个长度为Nm的向量（其中，Nm是总任务数），中标列表yi和中标航天器列表zi。每个航天器可以使用zi确定每个任务的出价最高者，并使用yi确定最高出价。当使用原始CBBA共识算法处理多航天器任务的数据时，不同的任务可以分配不同数量的航天器，对于需要多个分配的任务，向量不能存储每个分配的数据。因此，为了解决需要多航天器的任务分配问题，需要改变存储这些值的方式，必须将这两个向量转换成一个矩阵，以确定多个获胜者及其出价。

将这两个向量组合成一个包含所有拍卖获胜信息的信息矩阵B。矩阵使用行来显示任务，使用列来显示航天器，Bij对应于航天器i对任务j的出价，如果航天器尚未出价，则为0。此外，矩阵B的大小为Nn*Nm，其中Nn是在轨航天器数，每行中的非零值的数目不应超过任务所需的航天器数Lj。除此之外，还使用来区分每个航天器的本地数据，＞0表示航天器i认为任务j分配给航天器m，算法1给出了如何将zi、yi转换成矩阵集。

算法1：构造航天器i的信息矩阵B

2.3.2 分配冲突解决规则

原CBBA算法使用一个查找表来确定是根据发送者的信息更新还是重置接收者的信息。对于需要多航天器解决的任务，接收者不必重置或更新与自己不同的数据，而更可能合并数据，从而使两个航天器的数据都是正确的和保存的。新的分配冲突解决算法分为两个阶段，以便更好地结合航天器的数据，应对任务的多样性。

第一个阶段是将航天器的时间信息与它接收的所有数据进行比较，并接受更新的数据。通过比较航天器的时间戳信息，可以知道哪个航天器的数据比较新。在算法2中的4-8行，skm＞sim表示k有更多的最新通信数据，这些数据可能是更高的出价或更多的最新分配信息，应该保存。

在第二阶段，如果所有发送方和接收方当前都是最新的信息，根据发送方的数据更新接收方的数据。首先检查发送方k认为的分配给每个任务j的航天器m（算法2中第10-11行）。如果航天器i认为该任务没有分配给航天器m（=0），并且分配给任务j的航天器数量还没有达到该任务的需求数量，那么可以通过直接更新分配矩阵，将任务j同时分配给航天器i。

另外，当任务j的分配完成或有更好的出价时，应该按算法2中第12-14行更新任务j的分配矩阵。当接收者认为任务j的分配已满时，我们首先在分配给任务j的航天器中找到出价最低的航天器。如果发送者k认为出价高于此值，应该用发送者的数据替换最低出价，用更新新的分配矩阵（其中n是最低的投标航天器）。这里也可能有一个问题，当最小出价等于发送者的数据时，就可能出现死锁。因此，制定一个简单的规则，当航天器的出价相等时，ID较高的航天器具有优先级（算法2中的第15-19行）。

算法2：航天器i的分配冲突解决

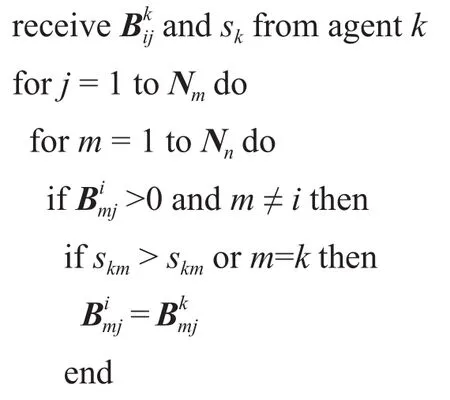
3 仿真结果及分析

本文中用于测试上述算法的仿真场景包括两种异构航天器（运输航天器和装配航天器），它们负责完成两类任务（运输和安装），每个任务所需的航天器数量可以单独定义。每个任务都有5min的时间窗口，一个随机的开始时间，以及5min或15min的任务执行时间。每个航天器都有自己的速度和特定的燃料消耗。

本文进行了以下仿真实验：每次实验包含20个任务，其中一半是运输任务，一半是装配任务。第一个实验验证了本文设计的竞价函数的有效性，其中每个任务只需要1个航天器完成；第二个实验验证拓展一致性算法，每个任务需要2个航天器完成；第三个实验设置为混合实验，运输任务需要2个运输航天器，装配任务需要1个装配航天器。每个实验的目标是最大化完成任务的所有航天器的奖励总和。多航天器任务将奖励完成任务的每个航天器，显示此类任务的难度和重要性，逐渐增加异构航天器的数量来测试算法性能。每个实验运行100次并记录平均数据。

图2显示了实验1的具体分配细节，图2（a）显示了每个航天器随时间的分配路径（为了更直观显示分配情况，只显示了x方向随时间的位置变化），图2（b）显示了每个航天器的具体分配时间表。从图中可以看出，含新竞价函数的分配算法可以成功处理具有复杂时间约束的在轨装配任务分配问题。

图3（a）显示了随着航天器数量的增加，三个实验的总分变化情况。可以发现，在实验开始时，由于异构航天器数量不足，多智能体任务的得分低于单一智能体任务的得分，但随着航天器数量的增加，多智能体任务的得分明显高于单航天器任务。图3（b）显示计算时间只会随着航天器数量的增加而增加，并且不会由于实验任务的类型变化而发生明显变化，它表明新的一致性算法不会导致计算量的增加。

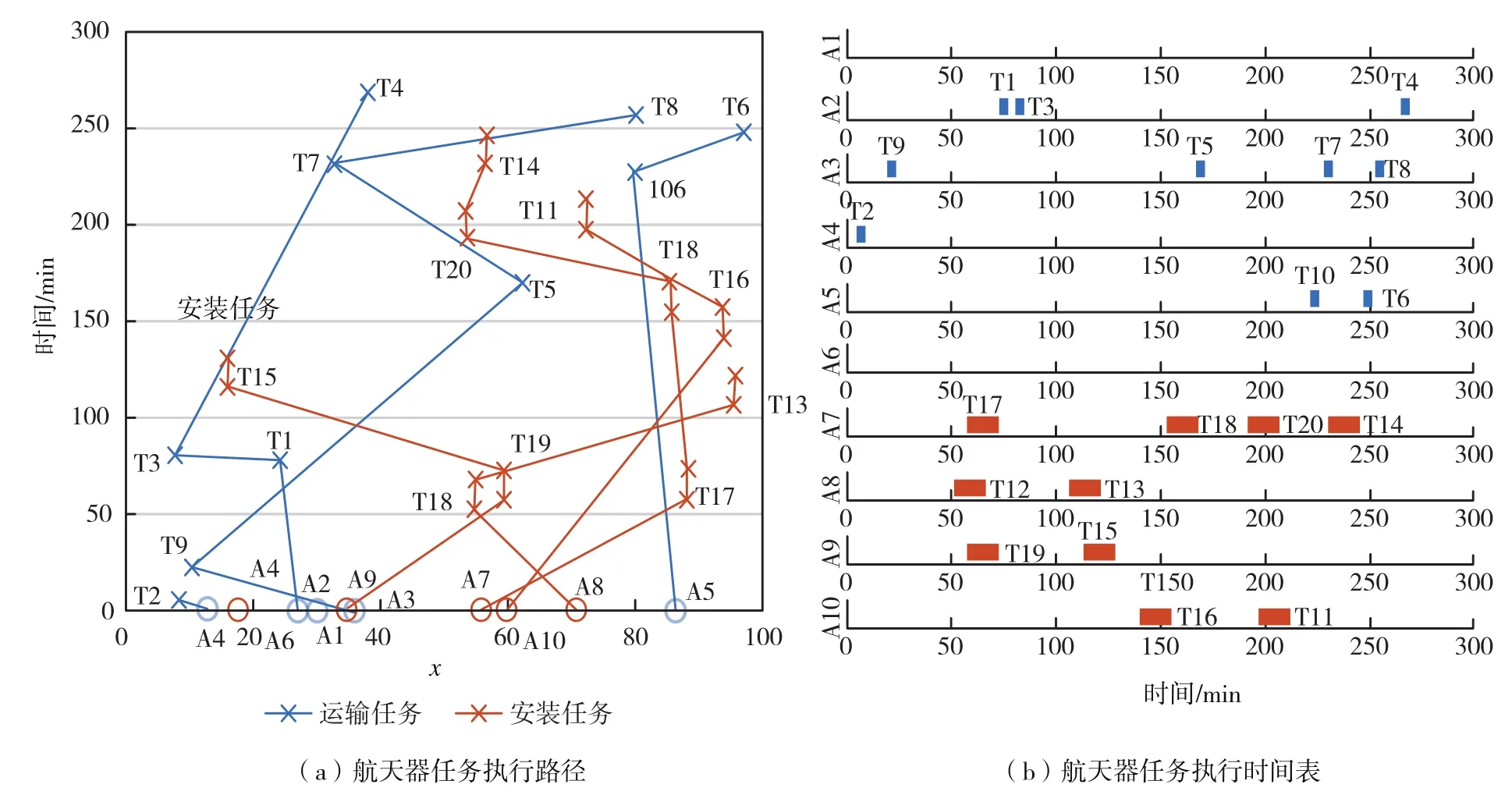
图2 实验一任务分配细节（共10个航天器，5个运输航天器，5个安装航天器）Fig.2 The first experimentation task assignment details（10 spacecrafts, 5 transport spacecrafts, 5 installation spacecrafts）

图3 各实验的实验性能对比Fig.3 Experimental performance between the Single-Agent, Multi-Agent and Mix experiments

图4 实验二任务分配细节（共10个航天器，5个运输航天器，5个安装航天器）Fig.4 The second experimentation task assignment details (10 spacecrafts, 5 transport spacecrafts, 5 installation spacecrafts)

值得注意的是，多航天器任务的通信步骤少于单航天器任务，这可以通过图4中航天器的分配细节解释。图4显示了共10个航天器执行多航天器任务的分配细节。

与单个航天器任务实验中每个任务需要选择最佳航天器相比，在执行多航天器任务过程中，当多个航天器组成团队完成第一个任务时，他们通常会一起执行下一个最近的任务，从而减少通信和距离成本。当然，航天器也会通过一致性算法形成一个更佳选择的新团队完成任务。但总的来说，这种现象减少了航天器之间的分配冲突，减少了通信步骤的数量。

4 结 论

本文提出了一种改进的CBBA算法，它为大型空间结构的在轨装配任务分配问题提供了一种分布式解决方法。算法的改进包括设计新的竞价函数使CBBA算法能够处理具有复杂时间约束的在轨装配任务，以及针对某些需要多航天器协同完成的特定复杂任务提出了扩展一致性算法，针对多智能体任务的分配冲突，将原CBBA算法中的中标名单和中标代理名单组合成一个包含所有中标信息的矩阵，并设计了新的冲突解决规则，解决了多代理任务引起的分配冲突。

本文通过仿真实验验证了该算法的有效性。实验表明，本文设计的含新竞价函数的分配算法可以成功处理具有复杂时间约束的在轨装配任务分配问题。同时，提出的扩展一致性算法成功解决了复杂多智能体任务的分配问题，且在不增加算法的运行时间情况下显著提高了分配任务总得分。综上所述，本文提出的分布式任务分配算法可以得出多航天器任务分配问题的无冲突解决方案，可以保证复杂在轨装配任务的成功分配。