基于最小一致性的自治式水下机器人路径规划

2019-10-31姚鹏，王琨

无人系统技术 2019年4期

姚鹏，王琨

（中国海洋大学工程学院，青岛 266100）

1 引言

作为一种具备自主导航与规划能力、可代替人类执行水下作业任务的无人运载平台，自治式水下机器人（Autonomous Underwater Vehicle，AUV）代表了水下航行器的未来发展方向，已逐渐应用于军用或民用领域［1-2］。现阶段，随着水下应用领域与应用需求的不断扩大、任务场景与任务要求的日益复杂，如何进一步提升AUV的自主航行能力与环境适应性，成为亟待解决的关键问题。而结合近些年AUV领域的发展趋势可知，路径规划技术是提升AUV自主性能的关键技术之一，因此受到越来越多的关注［3-4］。

AUV路径规划问题［5］是指依据已知或实时探测的环境信息，选定优化目标（如路径长度最短、能量消耗最少、或航行时间最少等），规划一条从起点到终点的全局路径，且可躲避各类障碍物或威胁，确保航行安全；而当AUV沿全局路径航行时，如果遭遇突发障碍或威胁，需在上述基础上对局部路径进行重规划。现有的AUV路径规划方法主要借鉴了地面或空中机器人的相关方法，并结合水下环境特点与AUV性能约束而不断深入。针对AUV路径规划问题，国内外学者从不同角度进行了大量的研究，现有方法主要包括：路标图法如Voronoi图、通视图等［5-6］，空间分解法如A*、D*、Dijkstra算法［7-8］，随机规划法如快速扩展随机树（Rapidly-exploring Random Tree，RRT）［9-10］，数学规划法如模型预测控制、混合整数线性规划［11-12］，基于势场的方法如人工势场法、流体扰动动态系统（Interfered Fluid Dynamical System，IFDS）［13-14］，导引法如几何导引法，行为法如模糊选择左转/右转等机动行为，以及上述各种方法的组合。

空间分解法可处理航行区域内的不规则障碍物，使用灵活方便，受到了国内外学者的广泛关注，它主要包括空间建模与优化求解两步：首先对规划空间进行处理，如构建栅格地图，从而将路径规划问题建模为典型的优化问题，然后采用合适的优化搜索算法（数学优化方法（如动态规划法等）、智能优化方法（如遗传算法、粒子群优化等）、启发式方法（如A*、D*）等）寻找一系列连通的单元组成最优路径［7-8，15-18］。例如，Zeng Z等［16］首先将规划空间离散化为一系列包含控制点的壳状空间，然后采用量子粒子群优化方法获得最优配置排序，以规划AUV全局路径。朱大奇等［17］引入栅格信度函数和环境信息来更新自组织神经网络中的获胜神经元权值，以引导AUV在向目标航行的过程中安全避障，并且克服了传统方法中的速度跳变缺陷。Ferguson D等［18］在D*算法基础上引入线性插值，获得连续平滑的AUV路径。然而，现有的空间分解法仍具有路径不平滑、优化时间长等缺陷，难以兼顾路径质量与计算效率，需进一步从空间建模或优化求解等角度进行改进。

一致性理论是指系统中不同个体的状态值趋于一致或相等，目前已广泛应用于多智能体编队等领域［19］。文献［20］在传统最小一致性理论的基础上，首次提出了一种引入连接权重的分布式最小一致性算法，用于寻找离散化栅格空间内的最短路径，该方法创新性地从控制的角度对路径规划问题进行了阐述，经证明总能获得当前空间精度下的最优路径。但上述方法仅考虑了路径长度指标，在复杂海洋环境下往往需结合洋流场等因素建立能量消耗或航行时间等指标，该类指标更加合理，上述方法仅采用了传统的栅格化空间策略，路径平滑度较差，甚至不满足机器人运动约束。因此本文在上述最小一致性算法的基础上，引入多层邻居栅格策略，并基于能量消耗与平滑度指标确定各节点状态值及连接权重，构建节点图，实现AUV全局路径规划。考虑到AUV沿全局路径航行时可能遭遇突发威胁，还引入偏离度等指标重新定义节点图，以重规划AUV局部路径。

2 AUV路径规划问题描述

通常来说，依据已知的离线环境信息如海底地形障碍、洋流分布等，需首先离线规划一条从起点到终点、满足运动约束、可引导AUV安全躲避障碍物的全局最优路径。但当AUV沿该条路径航行时，其搭载的侧扫声呐或水下相机等可能会探测到一些突发威胁如海洋生物、未知地形等，此时需进行局部路径重规划，引导AUV偏离初始路径以避开突发威胁，并迅速回到初始路径。

AUV航行空间通常远远大于AUV自身尺寸，因此路径规划问题仅考虑AUV质点模型。本文将规划空间离散化为二维栅格地图，且每个栅格设定为自由状态（f=0）或占据状态（f=1），用来表示该栅格是否为障碍物/威胁空间，各栅格中心点可表示AUV的备选路径点，路径规划问题可简化为选取一系列的栅格并依次连接组成路径。为降低计算复杂度，传统方法仅将AUV所在栅格的周围8个栅格（即第一层栅格，L=1）作为下一时刻可选位置，但会大大降低规划路径的质量如平滑度等。考虑到本文采用的最小一致性方法的计算量较少，本文进一步扩大了备选邻居栅格的层数（L≥2），即下一时刻AUV不仅可移动至周围8个栅格，还可移动至更远处的栅格，从而提高路径质量。如图1所示，采用四层邻居栅格策略，AUV可由位置a直接移动到位置b，而传统方法下AUV需经过c、d、e等点才能到达d，后者的规划质量明显低于前者。

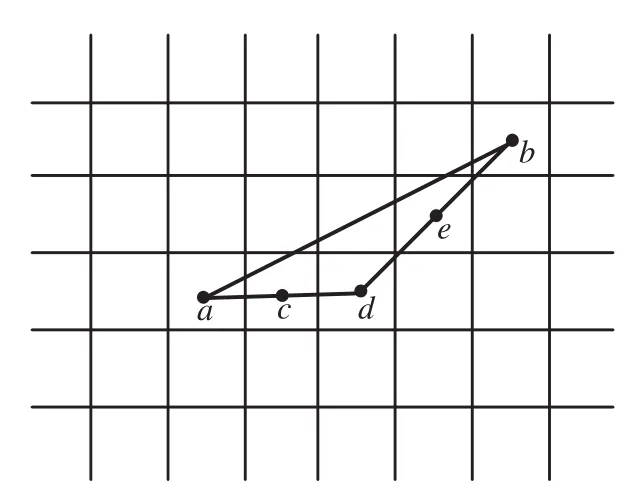
图1 栅格空间下的AUV运动示意图Fig.1 Illustration of AUV motion in grid-based space

3 基于最小一致性的AUV路径规划

3.1 最小一致性算法

首先，定义G=(V,E)为带权重的无向连接图，V={1,2,...,NV}表示各节点集合，E={(i,j)},i∈V,j∈V表示节点i和j连接，ai,j表示连接(i,j)的权重，令si和ui分别表示节点的状态值和控制输入，则节点状态方程可定义为。传统的最小一致性算法是指系统内的各节点到达稳定状态，其中si(0)表示节点的初始状态值，通常系统节点可分为Leader节点V1和Follower节点V2，各节点的控制输入可定义为：

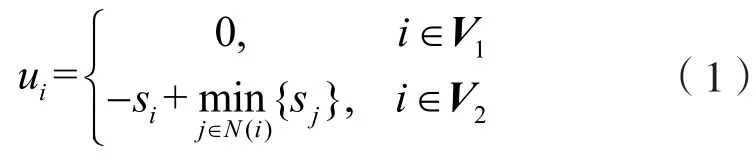
其中：N(i)表示节点i的邻居节点集合。通过更新各节点状态，系统最终到达稳定状态。

然后，可改进传统的最小一致性算法，使其能够适用于路径规划问题。AUV规划路径通常由一系列路径点组成，路径指标可定义为相邻路径点间的各路径段指标之和，因此可将所有的备选路径点作为图节点，当前路径点到终点的路径指标作为节点状态值，将相邻路径点间的路径段看作节点连接，路径段指标看作连接权重。各节点的控制输入将不仅取决于邻居节点状态值，还取决于本节点与邻居节点间的连接权重ai,j：

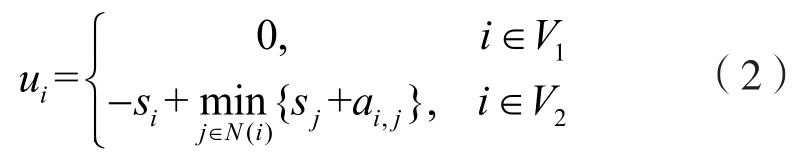
系统最终将到达如下稳定状态［20］：

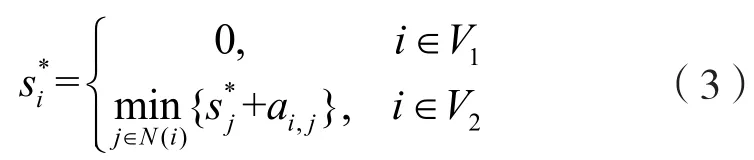
3.2 基于能量最优的AUV全局路径规划

3.2.1 全局路径优化指标

众所周知，AUV携带能量有限，沿路径航行所需要的能量越少，路径性能越好。本文主要采用能量指标来衡量全局路径的优劣，为使得规划路径易于跟踪，提升路径可行性，引入平滑性指标。AUV航行时必须满足环境约束即躲避障碍物，在计算上述指标之前，需首先判断规划路径是否成功避障，如果不满足环境约束，则直接引入无穷大的惩罚项。

假设全局路径为X={P1,…,Pm,…,PM}，其中P1，PM分别表示AUV起点和终点，则能量指标可定义如下［21］：

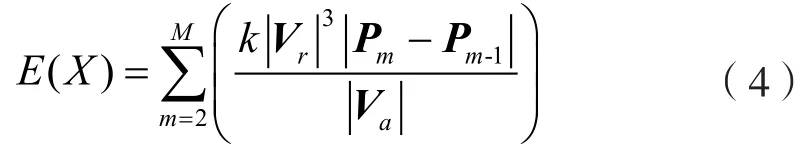
其中：k 表示AUV拖动常量，Vr表示AUV相对于洋流的速度（相对速度），Va表示AUV相对于大地的速度（绝对速度），定义Vc为洋流速度，则三者的矢量关系为：

平滑性指标可用全局平滑度来表示：

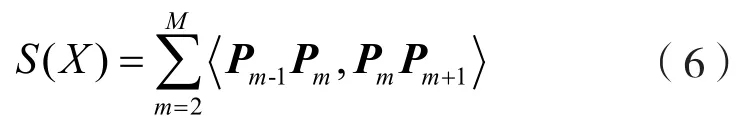
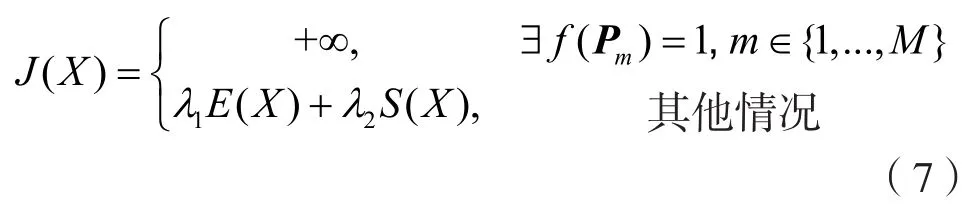
其中：λ1和λ2分别表示两类指标的权值。基于上述综合指标，AUV可在避开障碍物的前提下，尽可能消耗较少的能量并平滑地从起点到达终点。

3.2.2 最小一致性算法用于AUV全局路径规划

为将最小一致性算法用于解决路径规划问题，首先，需将AUV航行空间构建为对应的节点图。假设规划空间已离散化为N×N个栅格，从中可选取未被障碍物占据的栅格点作为图节点V，进而根据备选邻居栅格的层数来确定邻居节点，构建节点图。将任意节点i的状态值si定义为按式（7）计算的从当前节点i 到终点的路径指标值，以终点PM为Leader节点且其初始状态值为0，以其他节点为Follower节点且初始状态值设置为大于0的任意值，相邻节点间的连接权重ai,j可定义为：

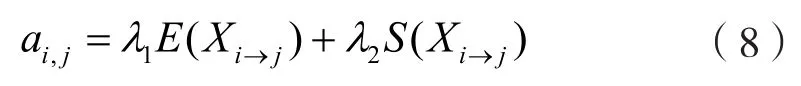
其中：Xi→j表示节点i和j 之间的路径段，能量代价和平滑性代价分别由式（4）和（6）计算获得。

然后，各节点采用改进的最小一致性算法，即利用式（2）迭代计算控制输入值ui并更新状态值，最终系统到达稳定状态即式（3）。需注意的是，不管节点初始状态取何值（但需大于0），经过有限步迭代更新后系统总能到达稳定状态，因此该算法在不同场景下均具有较好的适应性与较高的计算效率。在稳定状态下，起点的稳定状态值即表示全局路径的最优指标值，因此从起点开始，依次寻找父节点（即从邻居节点集合中选取具有最小的节点）直至到达终点，即可获得全局最优路径。

3.3 基于最小偏差的AUV局部路径重规划

AUV沿着规划的全局路径航行时，可能会遭遇突发障碍或威胁，因此还需进行局部路径重规划，使AUV偏离初始路径以避开突发威胁，并迅速回到初始路径。在确保航行安全的前提下，本文把AUV偏离初始路径的程度作为主要指标，并考虑平滑性等指标。

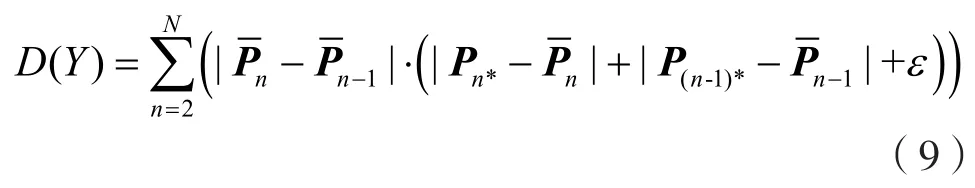
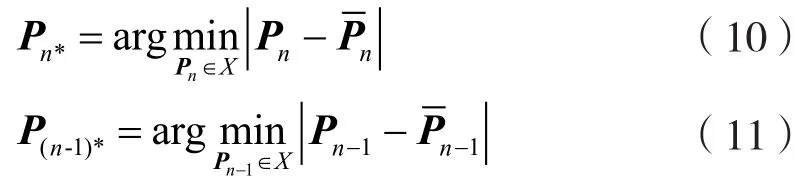
平滑性指标定义为：

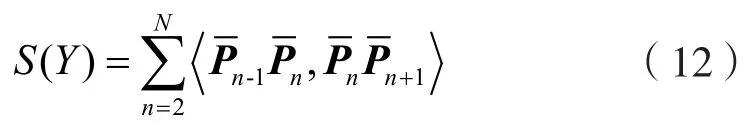
因此路径指标为：

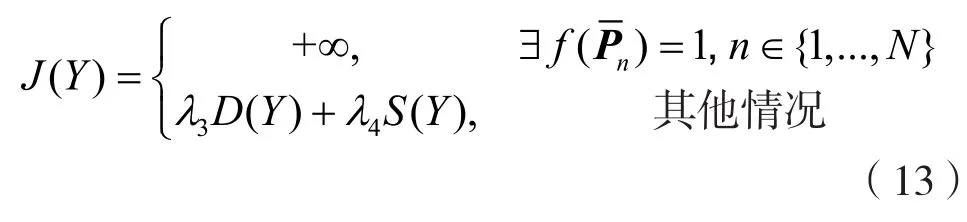
其中：λ3和λ4分别表示两类指标的权值。基于上述指标，AUV可在避开障碍的前提下尽可能靠近初始路径航行。

然后，采用最小一致性算法获得最优局部路径。节点图的构造方式类似于章节3.2.2，但需将节点状态值si定义为按式（13）计算的从当前节点i 到终点的指标值，而相邻节点间的连接权重ai,j可定义为：

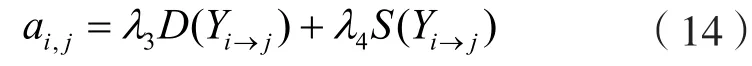
其中：Yi→j表示节点i和j 之间的路径段，偏离度代价和平滑性代价分别由式（9）和（12）计算获得。最终起点的稳定状态值即表示最优路径指标值，可通过迭代寻找父节点，最终获得局部路径。

此外，为减少系统迭代收敛到稳定状态所需的时间，可将全局路径点集合对应的节点的初始状态值均设置为0，并且当起点的状态值到达稳定时即可结束迭代过程。

4 仿真结果及分析

本文通过仿真实验来验证最小一致性算法用于解决路径规划问题的有效性。设定规划空间为1000m×1000m，栅格数为100×100，AUV绝对速率|Va|=2m/s，洋流场速率恒定，邻居栅格层数L=3，AUV起点为（0,0），终点为（1000,1000），AUV拖动常量k=1000kg。

某复杂场景包含多个随机生成的任意形状的障碍物，洋流场为正弦分布且速率恒定，图2表示采用最小一致性算法（MC）以及IFDS、RRT的规划结果，三种方法均能获得安全避障的全局路径。RRT方法规划的路径不平滑，甚至难以跟踪，可行性大打折扣；IFDS方法规划的路径虽然较平滑，但路径走向未沿洋流方向，消耗能量较多；而MC方法规划的路径在一定程度上顺流航行，消耗能量较少，且通过引入多层邻居栅格，使得路径较平滑。经统计，基于MC、IFDS、RRT三种方法的能量消耗分别为4098kJ、5669kJ、5065kJ，说明MC方法可获得能量最优的全局路径。此外，考虑到RRT等方法的随机特性，本文分别在50种场景下进行了仿真对比，经统计MC方法每次都能获得最优的全局路径，具有较好的环境适应性与鲁棒性。

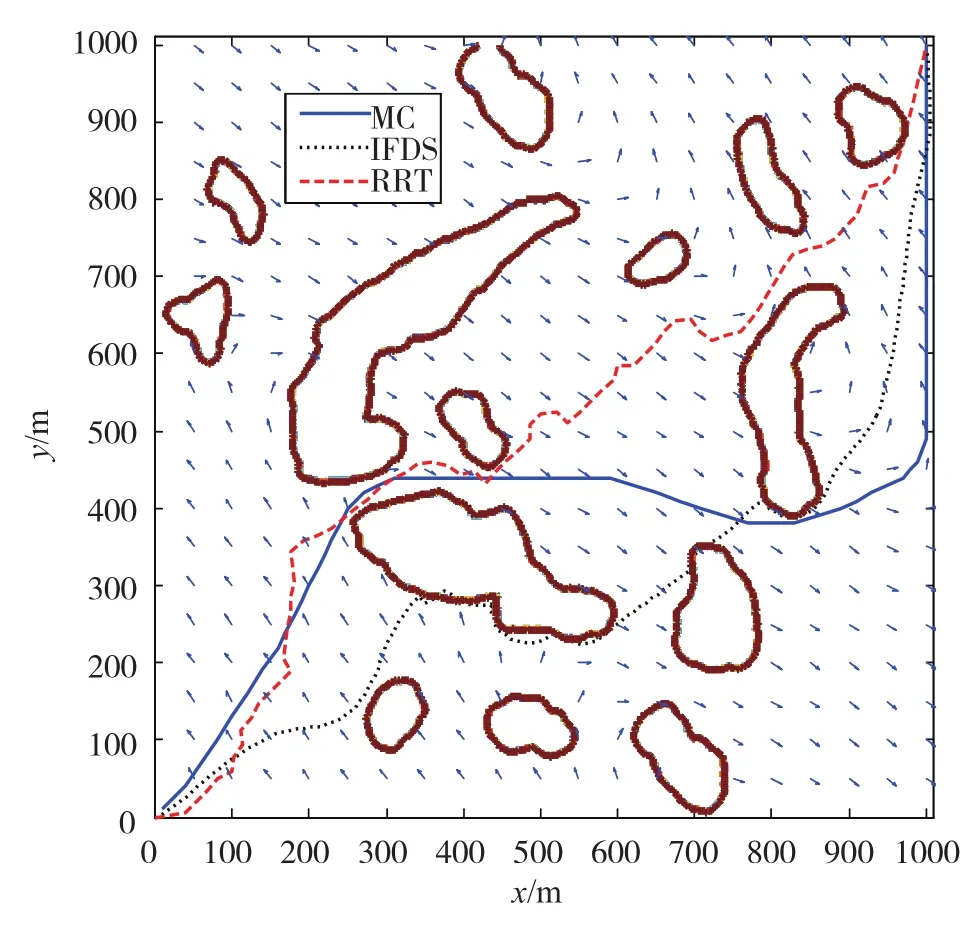
图2 采用不同方法的AUV路径规划结果Fig.2 AUV path planning results by different methods

图3给出了选取不同的邻居栅格层数（L=1,2,3）时的规划结果，其中L=1表示传统的栅格法。显然，通过增加邻居栅格层数，可以大大提高规划路径的平滑度，减少AUV能量消耗（分别为4389kJ、4150kJ、4098kJ）。但随着栅格层数增多，算法计算量将大大增加，而规划性能的提升有限，因此需选取兼顾计算量与优化性能的层数（本文选取L=3）。

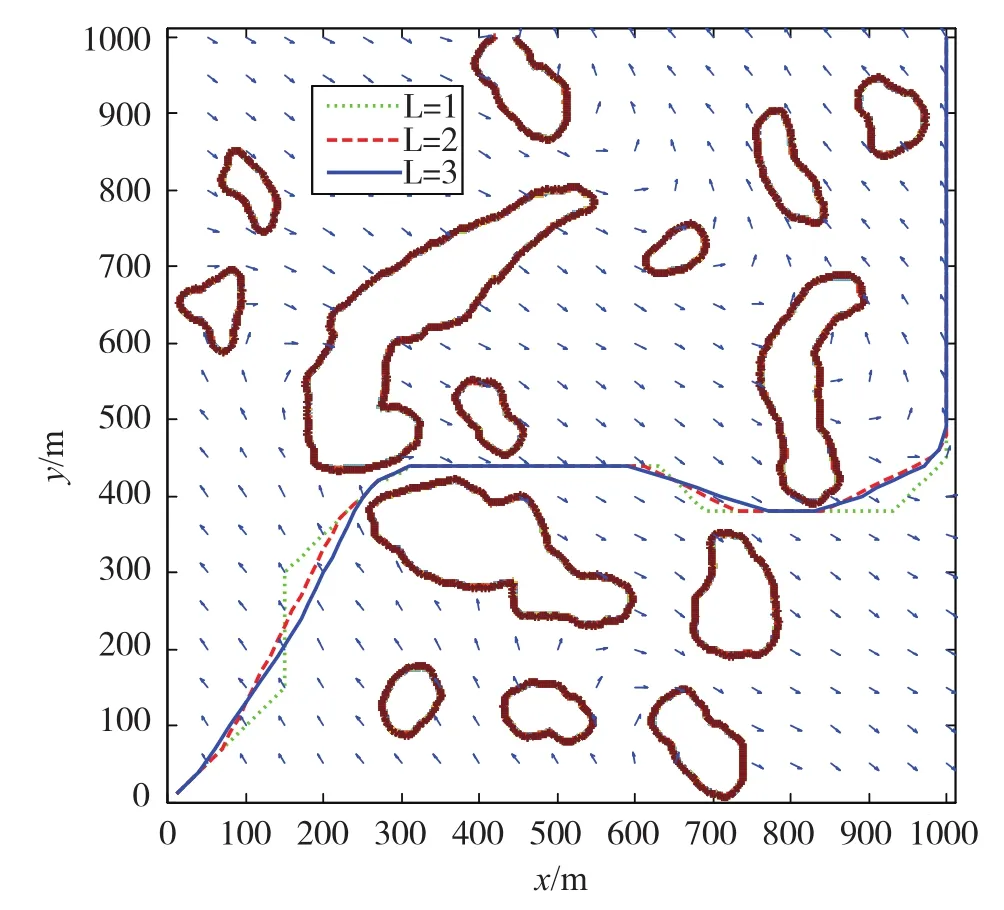
图3 采用不同L的AUV路径规划结果Fig.3 AUV path planning results with different L

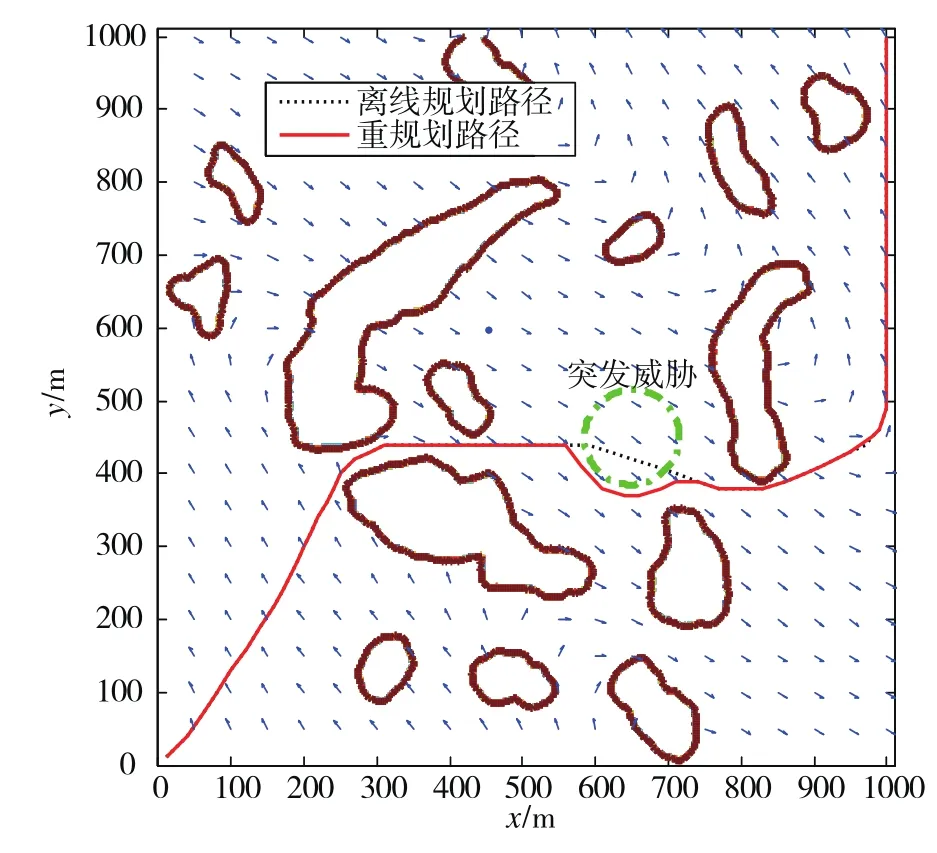
图4 基于最小一致性的 AUV路径重规划Fig.4 AUV path re-planning by minimum consensus

在上述已知场景基础上，假设还存在一个未知的突发圆形威胁，如图4所示。当AUV沿初始路径航行到（500,440）时才探测到该威胁，此时再次采取MC方法进行局部路径重规划。仿真结果表明，AUV会偏离初始路径即离线规划路径，以躲避该突发威胁，在避开威胁后AUV迅速回到初始路径，重规划路径的偏差程度较小、平滑度较好。