基于深度强化学习的行星车路径规划方法研究

周思雨，白成超

（哈尔滨工业大学航天学院，哈尔滨 150001）

1 引 言

近太空技术的不断发展与逐步成熟，掀起了人类不断向深外太空拓展的热潮。近年来，世界主要航天大国都相继制定了宏伟的深空探测长远规划与实施方案，例如美国、欧洲、日本以及俄罗斯［1-2］。在这些规划中，重返月球（Return to the moon）、火星2020（Mars2020）、火星外空生物学（Exobiology on Mars，ExoMars）等探测任务都将研制最先进的行星车。中国的嫦娥三号探测器携带玉兔号月球车实现了深空测控通信技术的突破；嫦娥四号探测器携带玉兔二号月球车实现了月球背面巡视探测技术的突破；未来计划发射的嫦娥五号探测器将对月面土壤进行采样并返回。2016年由国务院发布的《“十三五”国家科技创新规划》指出，“到2020年发射首颗火星探测器，突破一系列核心关键技术，在一次发射的基础上，实现火星环绕以及着陆巡视探测”。由此可见，行星车在航天领域的深空探测方向具有重大的研究意义。

行星车在星体表面运动时，要求其具备良好的自主能力，按照《新一代人工智能发展规划》中的论述，其关键技术为规划、感知和控制等。其中，路径规划是指在起点和目标点（给定环境）之间搜索出一条最优路径，它是行星车的中枢神经系统，是其能够安全高效地开展科学巡视探测的重要保证［3］。

按照地图信息获取方式的不同，将行星车的路径规划分为全局路径规划（基于先验地图信息）和局部路径规划（基于传感器信息）。研究方法可以分为传统方法和基于学习的方法。在传统方法中，行星车的所有行为都是预先定义好的。典型代表如美国喷气推进实验室（Jet Propulsion Laboratory，JPL）为一系列火星车开发的车辆任务序列与可视化系统（The Rover Sequencing and Visualization Program，RSVP）。地面工作人员可以通过RSVP快速复现的精确三维环境信息来制定行星车的任务序列［4-5］。选用RSVP是由于行星表面地形复杂，容易引起滑移和滚翻，导致任务失败。传统的方法在这种情况下可以增加系统的可靠性。

然而，未来的行星车需要做出战略转变，将以大规模科学探测为主。高价值的科学探测目标往往需要宇航员与多移动机器人协同作业，因此伴随着更为复杂的环境。对于行星车而言，作业环境不是完全已知的，需要其具备一定的对环境变化的自适应能力和自学习能力。因此需要研制出更高级的智能规划模块。此时，基于学习的规划框架就充分发挥了它的优势。在基于学习的方法中，深度学习（Deep Learning，DL）可以成功处理高维信息；强化学习（Reinforcement Learning，RL）可以在复杂环境下执行连续决策任务。如图1所示，将RL和DL结合在一起的深度增强学习（Deep Reinforcement Learning，DRL）可以学习一个端到端（End-to-end）的模型，尽可能地简化从感知到决策之间的人为操作，从而避免精密而脆弱的人工设计，进一步提升任务的稳定性和智能性。

图1 深度强化学习框架Fig.1 Deep reinforcement learning framework

基于以上需求背景，本文以行星车为应用背景，研究一种在行星探测环境中应用的基于DRL的路径规划方法。首先通过DL处理从环境中获取的多源传感器组成的状态信息，然后利用RL基于预期回报评判动作价值，将当前状态映射到相应动作，并将动态指令分配给行星车。作为算法验证，本文将深入探索较为高效的基于DRL的方法，并将其应用于多传感器行星车的路径规划中，赋予行星车对环境变化的自适应能力和自学习能力，同时在基于机器人操作系统（Robot Operating System，ROS）及Gazebo的仿真场景中验证算法的有效性。这种DRL算法具有非常广泛的应用，对于航天领域以及机器人领域中的自主规划等都有非常重要的意义。

2 DQN及其衍生算法

早期，研究者就尝试将神经网络与RL进行集成，但当把离策略（Off-policy）、函数近似和引导（Bootstapping）结合在一起时，RL会表现出不稳定，甚至开始发散。直到DeepMind团队的Mnih等［6］创造出DQN，这才点燃了DRL领域。

此后，DQN得到了广泛的发展，图2给出了DQN的发展历程，将其中的DQN、Double DQN和Dueling DQN算法融合在一起，结合PER算法就构成了D3QN PER算法。

2.1 DQN算法

2.1.1 经验回放

在DQN中使用经验回放的动机是：作为有监督学习模型，深度神经网络（Deep Neural Network，DNN）要求数据满足独立同分布假设；但样本来源于连续帧，这与简单的RL问题（比如走迷宫）相比，样本的关联性大大增加。假如没有经验回放，算法在连续一段时间内基本朝着同一个方向做梯度下降，那么在同样的步长下，这样直接计算梯度就有可能不收敛。所以经验回放的主要作用是：克服经验数据的相关性，减少参数更新的方差；克服非平稳分布问题。经验回放的做法是从以往的状态转移（经验）中随机采样进行训练，提高数据利用率，可以理解为同一个样本被多次使用。

2.1.2 算法原理

神经网络的训练可以理解为通过最优化损失函数使其最小化，这里的损失函数指的是标签和网络输出的偏差。为此，DQN算法利用Q-learning为Q网络提供有标签的样本，再通过反向传播使用梯度下降的方法更新神经网络的参数。

（1）采用DNN作为Q值的网络：

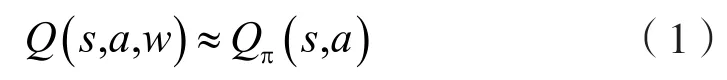
其中，w为DNN的参数。

（2）在Q值中使用均方差（Mean Square Error，MSE）定义损失函数：

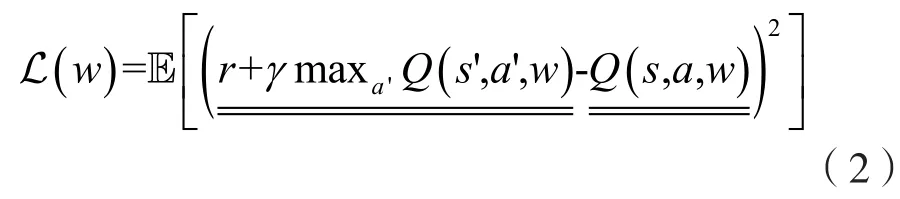
（3）计算参数w关于损失函数的梯度：

图2 DQN的发展历程Fig.2 Development of DQN

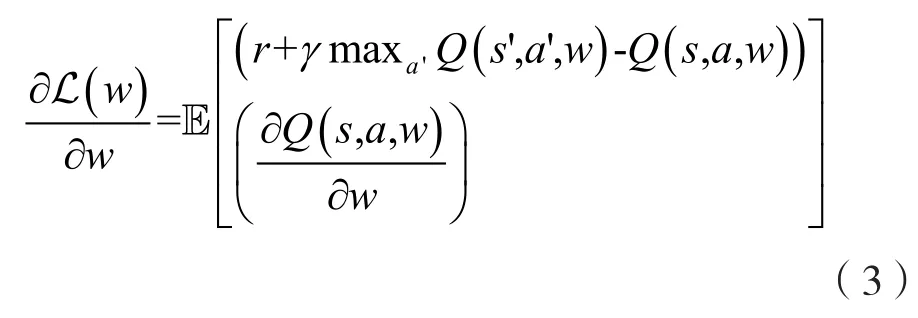
（4）使用随机梯度下降法（Stochastic Gradient Descent，SGD）更新参数，从而实现端到端的优化目标。

本文采用的DQN算法还引入了一个与当前值网络结构一致的目标值网络，负责生成训练过程的目标，即。每训练C步，将当前值网络的参数完全复制给目标值网络，那么，接下来C步参数更新的目标将由更新后的目标值网络负责提供。

2.2 Double DQN算法

2.2.1 优先经验回放

PER的思路来源于优先清理（Prioritized Sweeping），它以更高的频率回放对学习过程更有用的样本，本文使用TD-error来衡量作用的大小。TD-error的含义是某个动作的估计价值与当前值函数输出的价值之差。TD-error越大，则说明当前值函数的输出越不准确，换而言之，能从该样本中“学到更多”。为了保证TD-error暂时未知的新样本至少被回放一次，将它放在首位，此后，每次都回放TD-error最大的样本。

本文结合纯粹的贪婪优先和均匀随机采样。确保样本的优先级正比于TD-error，与此同时，确保最低优先级的转移概率也是非零的。

具体的，定义采样转移i 的概率为：

其中，pi是第i 个经验的优先级；指数α决定使用优先级的多少，当α=0时是均匀随机采样的情况。主要存在两种实践途径，第一种是成比例的优先（Proportional Prioritization），即

其中，δi为TD-error；ε是为了防止经验的TD-error为0后不再被回放。

在实现时采用二叉树结构，它的每个叶子节点保存了经验的优先级，父节点存储了叶子节点值的和，这样，头节点的值就是所有叶子结点的总和。采样一个大小为k 的minibatch时，范围[0,ptotal]被均分为k 个小范围，每个小范围均匀采样，各种经验都有可能被采样到。

第二种是基于排行的优先级（Rank-Based Prioritization），即：

其中，rank(i)是经验池中根据TD-error排行的第i个经验的排行。

在概率统计中，使用某种分布采样样本会引入偏差，加入重要性采样（Importance-sampling）可以消除偏差。这里的重要性采样权重为：

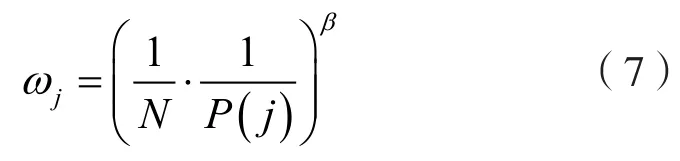
其中，β用于调节偏差程度，因为在学习的初始阶段有偏差是无所谓的，但在后期就要消除偏差。为了归一化重要性采样权重：

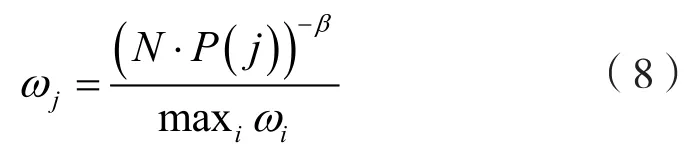
2.2.2 算法原理

Q-learning中存在严重的过估计问题，这个问题同样被带入到DQN算法中。假设所有动作在当前状态下的实际返回值都是0，但由于估计必定存在误差，所以一些动作可能返回正值（假设为+0.5），一些动作可能返回负值（假设为-0.5）。在Q函数返回所有动作在当前状态下的估计值后，Q-learning选择最大Q值的动作。但此时这个最大值是+0.5，并且每一步（在每个状态下）都存在该问题。随着迭代往前进行，过估计问题可能导致策略逐渐变为一个次优解。为解决过估计问题，Double DQN应运而生［7］。它将目标Q值中动作的选择和动作的评估分开，让它们使用不同的Q网络。在DQN中的目标Q值为：，而在Double DQN中的目标Q值为

2.3 Dueling DQN结构

如图3所示，Dueling DQN［8］相比于DQN在网络结构上做出了改进，在得到中间特征后，一边预测状态值函数v(s;θ,β)，另一边预测相对优势函数A (s,a;θ,α)，两个相加才是最终的动作值函数：

其中，s、a分别为当前状态和动作；θ为卷积层参数；β和α是两支路全连接层参数。这样做的好处是v(s)和A(s,a)分别评定远近目标，v(s)是对当前状态的长远判断，而A(s,a)则衡量在当前状态下不同动作的相对好坏。

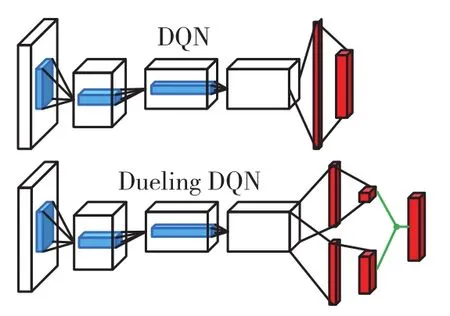
图3 Dueling DQN的网络结构示意图Fig.3 Network structure diagram of dueling DQN

训练时，如果按照式（9）的做法，给定一个Q值无法得到唯一的ν和A，比如，ν和A分别加上和减去一个值能够得到同样的Q值，但反过来显然不行。根据式（9），最优状态值函数ν*来源于使Q值最大的那个贪婪动作，即。由此，可通过强制使得选择贪婪动作的优势函数为0，来保证分离出来的ν就是最优策略下的ν*。所以取：

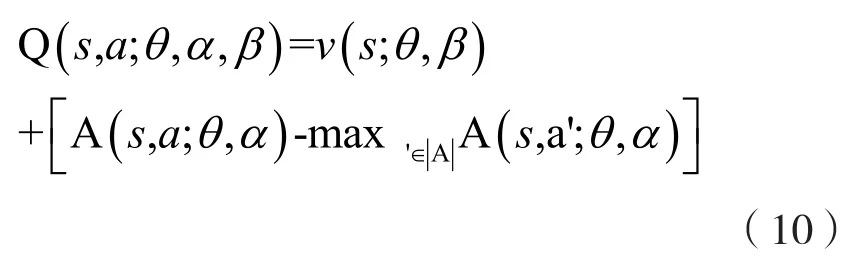
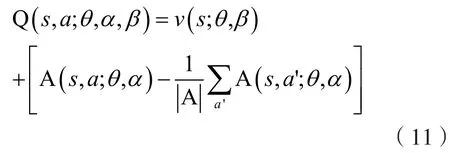
这个操作会偏离目标函数，A不再为0，但可以保证该状态下各动作的优势函数相对排序不变，而且可以缩小Q值的范围，去除多余的自由度，提高算法的稳定性。

3 行星车环境特征处理方案

3.1 自身状态信息处理方法

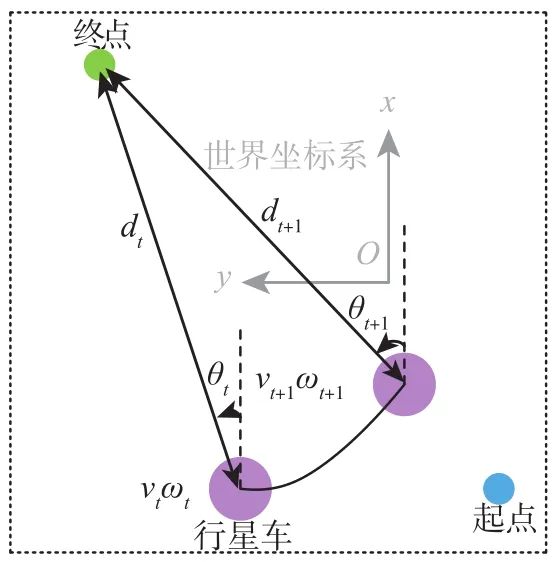
图4 自身信息处理方法示意图Fig.4 Schematic diagram of its own information processing method

3.2 激光雷达点云信息处理方法

激光雷达（Light Detection And Ranging，LIDAR）能适应不同的光照，同时对环境具有较好的鲁棒性，因此成为近期行星车发展中最重要的传感器之一。

LIDAR产生的点云属于长序列信息，比较难直接拆分成单个独立的样本通过CNN进行训练。本文采用长短期记忆（Long Short-Term Memary，LSTM）网络处理LIDAR点云信息，其中cell单元为512个，具体的网络结构如图5所示。

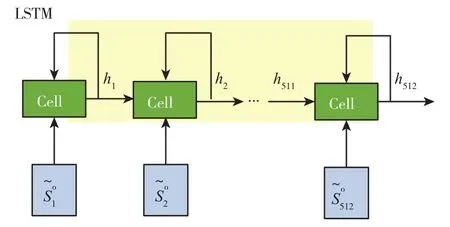
图5 处理LIDAR点云信息的LSTM网络结构示意图Fig.5 Schematic diagram of LSTM network structure for processing LIDAR point cloud information

为了方便，控制LIDAR输出的点云信息为360维，更新频率是50Hz，探测范围为-90o～90o，探测距离为0.1～10.0m。

3.3 视觉图像信息处理方法

尽管LIDAR擅长测量障碍物的距离和形状，但实际上它并不能用于确定障碍物的类型。计算机视觉可通过分类完成这项任务，即给定相机的图像，可以标记图像中的对象。

本文采用CNN处理视觉图像信息。输入图像（1024×728）经过预处理和叠帧（4帧）后变为80×80×4的单通道灰色图。这里共采用了三个卷积层，它们分别是conv1、conv2和conv3。Conv1、conv2和conv3的具体参数可参见表1。

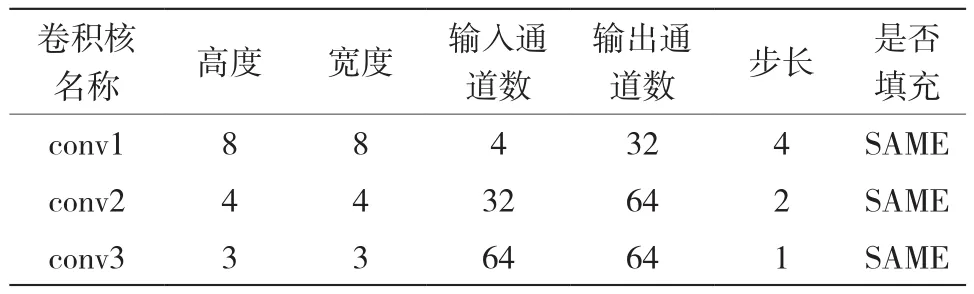
表1 卷积核参数Table 1 Convolution kernel parameter

3.4 环境特征融合方案

结合前面所提出的针对自身状态信息、LIDAR点云信息和视觉图像信息的处理方法，再结合D3QN PER算法，由此可以给出行星车的环境特征融合方案，如图6所示。

4 仿真结果及分析

4.1 行星车的动作空间划分

考虑到大规模行星探测作业环境的复杂性，首先将行星车的动作空间划分为11个单元，如表2所示。

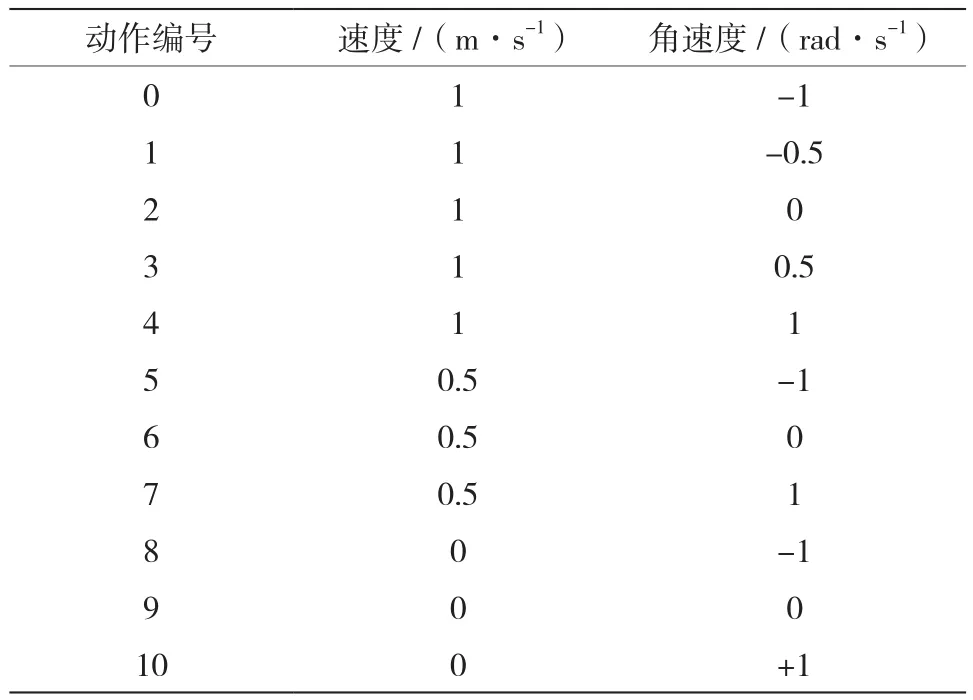
表2 动作划分表Table 2 Action partition table

图6 环境特征融合方案示意图Fig.6 Schematic diagram of environmental feature fusion scheme

4.2 算法参数与奖励函数设置

算法的基础参数设置如表3所示。为了加快收敛速度，є-贪婪法的є参数从初始值1.0开始按照训练步数线性下降，如式（12）所示，直到є等于єfinal后不再变化。

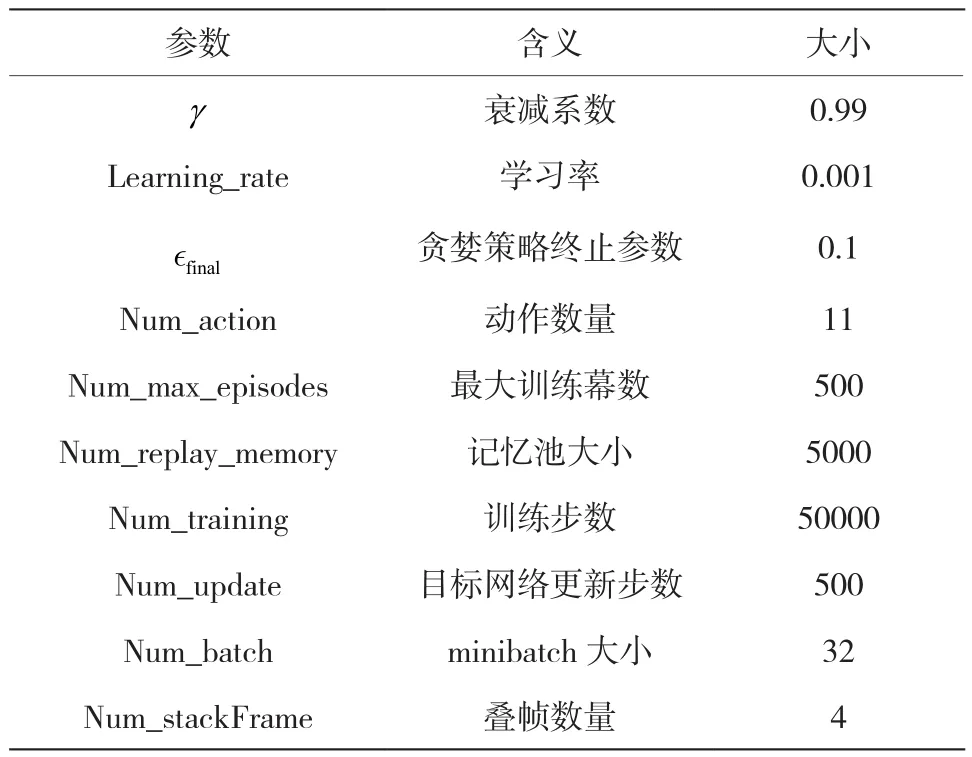
表3 参数设置表Table 3 Parameter settings table

PER算法的参数设置如表4所示。值得注意的是，β参数也按照训练步数线性下降：

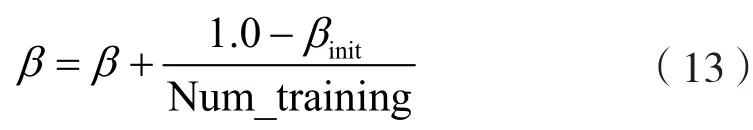
表4 PER算法参数设置表Table 4 PER algorithm parameter setting table

奖励函数的设置参见表5。其中，vt和vt-1分别为t时刻和t-1时刻行星车的速度信息；ωt和ωt-1为t时刻和 时刻行星车的角速度信息；dt和dt-1为t时刻和t-1时刻行星车相对终点的距离信息；θt和θt-1为t时刻和t-1时刻行星车相对终点的角度信息。

表5 奖励函数的设置Table 5 Setting of reward function

4.3 结果与分析

将沙砾和岩石简化为静态障碍，搭建的仿真环境如图7所示。

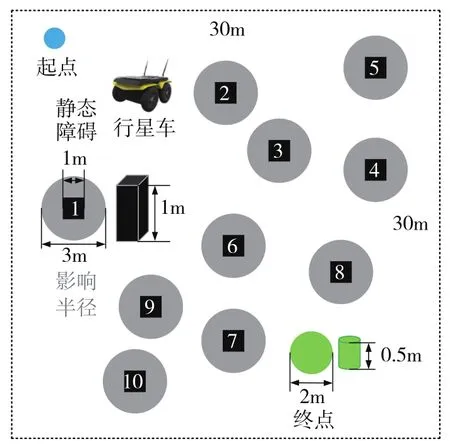
图7 仿真环境示意图Fig.7 Schematic diagram of simulation environment

其中，静态障碍为边长为1m的黑色正方体，影响半径为1.5m。在每一幕训练时，行星车的起点和终点以及静态障碍的位置都是随机的，为了模拟行星探测环境的复杂程度，它们需要满足以下条件：行星车的起点和终点之间的距离不小于20m；各静态障碍之间的距离不小于5m；各静态障碍与行星车的起点和终点之间的距离不小于5m。

训练过程中奖励随幕数的变化趋势如图8所示，由图可知，网络收敛。

随机生成的500幅地图进行测试，测试过程中奖励随幕数的变化趋势如图9所示。由图可知，500次测试中行星车全部到达了终点。

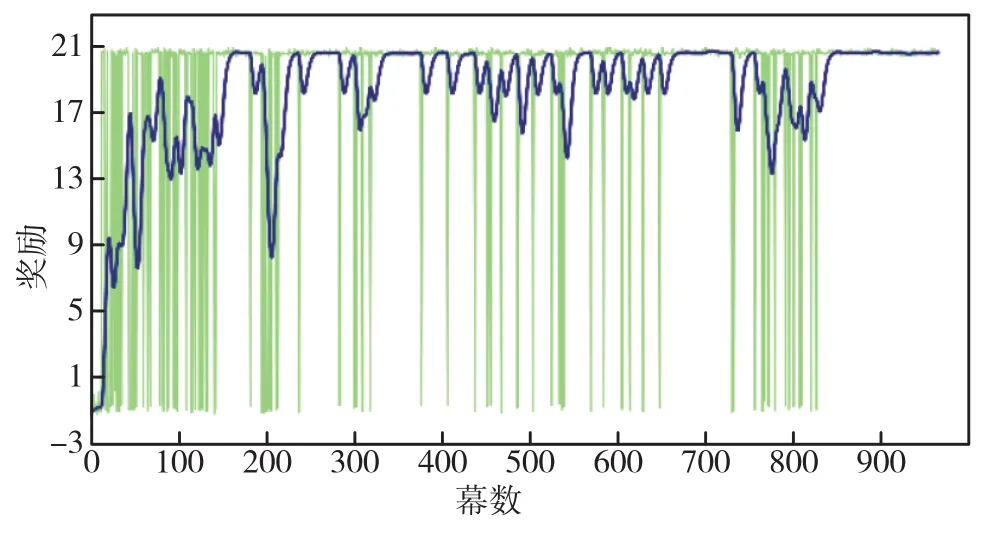
图8 训练过程中奖励随幕数的变化图Fig.8 Change of reward with episode during training

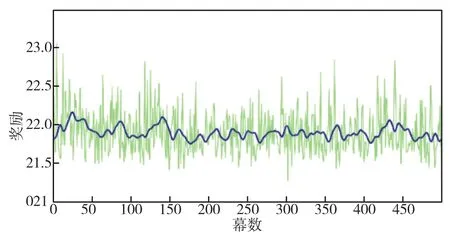
图9 测试过程中奖励随幕数的变化图Fig.9 Chart of reward change with episode during testing

展示测试中的地图，如图10所示，规划的路径不仅能够成功避障，并且较短较直。

图10 路径规划结果示意图Fig.10 Schematic diagram of path planning results

5 结 论

本文研究了行星车端到端的路径规划问题，将其应用于大规模行星探测背景下宇航员和多机器人协同作业的复杂环境中。使用CNN和LSTM处理多传感器信息，结合DQN、Double DQN、Dueling DQN和PER算法的优点，采用D3QN PER算法，赋予了行星车自主决策、自主学习以及自适应的能力。在静态障碍环境中进行了一系列实验，验证了该方法对不同环境的适应性，展示了其在航天领域深空探测行星车上的应用价值。