逼近无控旋转目标航天器的混合势函数安全制导

刘将辉，李海阳，陆林，赵剑

国防科技大学 空天科学学院，长沙 410073

航天器在空间中由于燃料耗尽或某部件发生故障时，将处于无控旋转状态[1-3]。为了使造价昂贵的航天器继续在轨运行，必须对航天器进行在轨修复、燃料加注或部件更换等[4-7]。面向无控旋转目标航天器的安全逼近是实施上述任务的基础。

相关学者在逼近无控旋转航天器方面做了大量的研究并取得了许多重要成果。Ma等[8]提出了前馈最优控制方法，将时间/燃料消耗作为优化变量，重点放在搜寻最佳逼近路径以及优化追踪航天器的推力分布。Xin和Pan[9]采用Thetas-D非线性最优控制方法，通过摄动过程求出Hamilton-Jacobi-Bellman(HJB)方程的近似解，设计了该问题的闭环反馈控制器。Martins-Filho和Jr[10]基于Clohessy-Wiltshire(C-W)方程建立了追踪航天器与无控旋转目标航天器的相对运动模型，分别采用线性二次调节器(LQR)和比例微分(PD)控制器进行控制，并对两种控制器的鲁棒性和跟踪能力进行了对比分析。Boyarko等[11]研究了圆轨道下逼近无控旋转目标航天器的最小能量和最小时间的轨迹优化问题，采用Pontryagin最小准则对最优控制问题进行分析并通过高斯伪谱法进行数值求解。Stoneman和Lampariello[12]提出了一种基于非线性优化的运动规划方法，通过在线全局搜索的并行优化法为追踪航天器逼近无控旋转目标卫星提供参考轨迹。考虑到控制输入饱和以及速度约束条件，Li等[13]提出模型预测控制策略以逼近无控旋转目标航天器。Zagaris和Romano[14]研究了逼近旋转目标航天器的可达性问题。李鹏等[15]提出追踪航天器沿旋转目标航天器最大惯量轴同步逼近的控制策略。姜博严等[16]采用滑模自适应控制方法，着重考虑了逼近旋转目标航天器的姿轨强耦合控制问题。作者团队[17]提出增广比例导引律方法，引入了跟随旋转目标航天器运动的逼近点概念。孙冲等[18]提出利用外包络法来优化追踪航天器路径。文献[8-18]在逼近无附件刚性航天器方面控制性能较好，当面对逼近具有太阳能电池帆板和天线等柔性航天器的问题时，则可能会导致追踪航天器与目标航天器太阳能电池帆板和天线等附件相撞，显然无法满足逼近过程的安全性要求。

为了保证航天器逼近过程的安全性，Breger和How[19]提出了一种主动安全方法，将交会对接过程中的安全性作为约束，在保证安全性的同时不额外消耗燃料。Park等[20]开发了一种模型预测控制器，能有效躲避碎片的撞击并有助于降低燃料的消耗。Chen等[21]利用人工势场法对4个柔性航天器进行在轨自主装配，所提控制策略使得服务航天器在到达期望位置的同时也避免了碰撞问题的发生。Dong等[22]引入了势函数法对追踪航天器的路径进行约束，提出了实时自适应控制律，在之后又提出了一种基于双四元数的特殊人工势场法来约束追踪航天器的轨迹[23]，张大伟等[24]利用基于椭圆蔓叶线的人工势函数制导，Zhu等[25]提出了模型预测控制法，Feng等[26]设计了一种基人工势函数的新型滑模控制策略，Cao等[27]设计了次优人工势函数滑模控制。Nicoletta等[28]将人工势场理论与滑模技术相结合设计了避障制导算法。作者团队[29]提出了追踪航天器沿旋转目标航天器某一体轴逼近的控制策略，设计了安全逼近轨迹。文献[19-29]很好地解决了安全逼近问题，但上述方法对追踪航天器的初始位置有要求，即追踪航天器的初始位置必须位于目标航天器本体坐标系的某一范围，否则追踪航天器仍然会与目标航天器的附件发生碰撞。

逼近无控旋转目标航天器方面的研究在取得大量成果的同时，也存在许多局限性，主要在以下两个方面：第一，航天器间的相对运动方程大多都是基于Clohessy-Wiltshire(C-W)方程的圆轨道描述，航天器间的相对位置和相对速度测量需要地面高精度的遥测和滤波，实时性较差并且位置误差较大。第二，为了满足安全逼近要求，对追踪航天器的初始位置有严格的限定。

基于上述考虑，本文以视线坐标系建立两航天器的相对运动方程，对任意偏心率的轨道均适用，追踪航天器与目标航天器的相对位置和相对速度的测量主要依赖于追踪航天器本身的传感器，实时性较好并且位置误差较小。其次，本文推导的方法对追踪航天器的起始位置没有要求，追踪航天器可以从任意位置对目标航天器进行逼近。最后，本文所提的方法不仅能安全逼近而且能躲避逼近过程中的飞行障碍物，安全性更高。

1 基础模型

1.1 相对运动方程

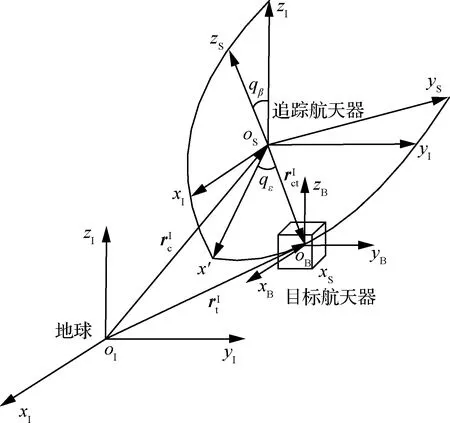
图1 相对运动坐标系统

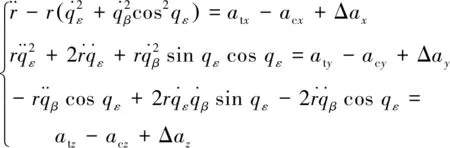
(1)

(2)

(3)

e1=r-rd=x1-rd

(4a)

e2=qε-qεd=x2-qεd

(4b)

e3=qβ-qβd=x3-qβd

(4c)

(4d)

(4e)

(4f)

ep=xp-xpd

(5)

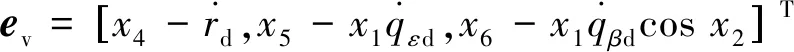
(6)

对式(5)和式(6)分别求导，可得

(7)

(8)

其中:

(9)

P2(x)=

(10)

1.2 姿态运动方程

为了方便分析，本文采用四元数描述航天器的姿态，四元数描述下的姿态运动学方程为

(11)

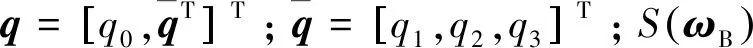
(12)

(13)

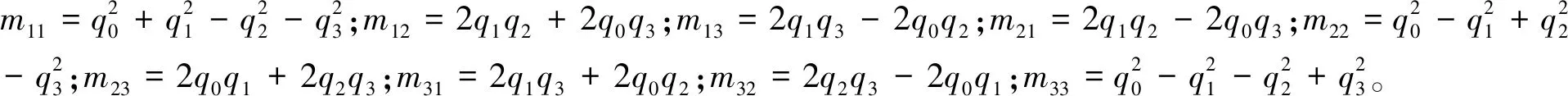
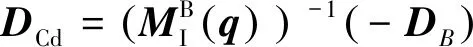
(14)

2 混合势函数与系统稳定性证明

混合势函数制导的原理为：定义能反映追踪航天器在全局运动趋势的混合势函数，该混合势函数由吸引势函数、安全势函数、障碍物势函数组成。用吸引势函数表示参考位置，参考位置对追踪航天器施加引力，混合势函数在参考位置具有全局最小值。用安全势函数表示安全区和安全走廊，安全区和安全走廊对追踪航天器施加斥力。用障碍物势函数表示障碍物，障碍物对追踪航天器施加斥力。安全区、安全走廊和障碍物构成了追踪航天器的路径限制区域。混合势函数在路径限制区域具有全局较大的值。利用Lyapunov稳定性理论分析混合势函数，找出合适的控制律使混合势函数的导数为负，从而使混合势函数保持单调递减。使得追踪航天器在到达参考位置的同时，也能有效地避开路径限制区域(安全区、安全走廊和障碍物)，以达到预期的制导目的。

2.1 吸引势函数

用吸引势函数表示参考位置，将吸引势函数设计为

(15)

式中：Qp和Qv为正定对称矩阵。由式(15)可知，当ep=0且ev=0时，Ωd=0，否则Ωd>0，参考位置(ep=0且ev=0)为该吸引势函数的最小值。

2.2 安全势函数

图2 安全区和安全走廊

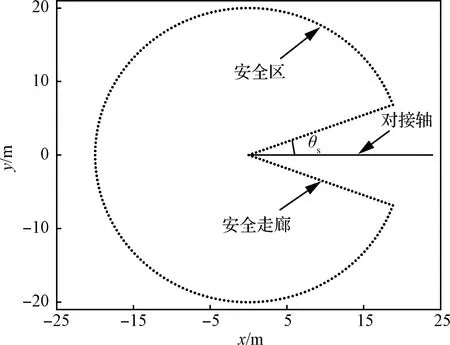
图3 安全区和安全走廊剖面

由图2和图3可知，可通过追踪航天器视线与目标航天器对接轴的夹角α与安全角θs的关系来划分安全区和安全走廊。当α>θs时，此时安全区起作用。当α≤θs时，此时安全走廊起作用。根据上述分析，可得

(16)

用Gaussian函数表示安全区和安全走廊，将安全势函数Ωs0设计为

(17)

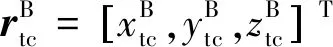
(18)

对式(17)求导可得

(19)

(20)

下面求解式(19)中的其他各项偏导数，

(21)

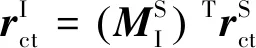
(22)

(23)

联立式(13)和式(18)可得

(24)

式中：

(25)

式中：

2.3 障碍物势函数

在逼近任务中，有时候需要伴飞航天器对无控旋转目标航天器进行全面的观察侦测。追踪航天器在逼近过程中应避免与伴飞航天器发生碰撞，此时伴飞航天器表现为障碍物。将障碍物看作是具有一定半径的球体，障碍物势函数Ωo0的设计为

(26)

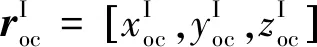
(27)

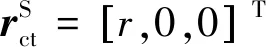
(4)压滤机。净化杂质的液固分离主要选用XAZGFN150/1250- U自动暗流隔膜压滤机。压滤机机座、压紧板、止推板材质为高强度Q345钢，前后机架、压紧板(包括地脚)玻璃钢防腐(≥3 mm厚)；主梁材质选用高强度桥梁钢外包2 mm厚 316L不锈钢；滤板材质为TPE弹性体无碱玻纤聚丙烯；滤布采用涤纶短纤747工业滤布；拉板机构链条、链盒、链轮材质均为316L不锈钢；渣斗、翻板为钢衬PE结构。

对式(26)求导可得

(28)

式中：

(29)

(30)

(31)

(32)

式中：

(33)

式中：

2.4 系统混合势函数

系统混合势函数Ω0为吸引势函数Ωd、安全走廊势函数Ωs0和障碍物势函数Ωo0之和，Ω0的表达式为

Ω0=Ωd+Ωs0+Ωo0=

(34)

由式(34)可知，Ω0的最小值不再精确位于参考位置状态。为了避免上述情况发生，将式(17)的安全势函数Ωs0和式(26)的障碍物势函数Ωo0重新定义，补充二次型系数，可得

(35)

(36)

Ω=Ωd+Ωs+Ωo=

(37)

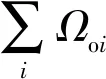
2.5 系统稳定性证明

取Lyapunov函数V为系统混合势函数Ω，即

(38)

由式(38)可知，V≥0。对式(38)求导可得

(39)

将式(7)和式(8)代入式(39)可得

(40)

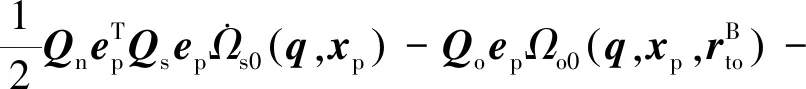
(41)

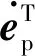
(42)

整理式(41)可得

at+as+ao

(43)

式中：

(44)

(45)

(46)

其中：at为目标参考位置对追踪航天器的引力加速度；as为安全区和安全走廊对追踪航天器的斥力加速度；ao为障碍物对追踪航天器的斥力加速度。将式(41)代入式(40)可得

(47)

证明完毕，因此所设计的系统具有稳定性。

(48)

由于追踪航天器的推力有限，因此其控制加速度有限，各方向的实际控制加速度为

(49)

式中：amax为追踪航天器单个方向所能提供的最大加速度;a为由式(48)所求得的加速度大小。

3 仿真分析

本文以追踪航天器相对无控旋转目标航天器超近距离段的交会对接任务进行数值仿真。为了形象分析吸引势函数、安全势函数和障碍物势函数的作用，本文设置了两组仿真场景，即

1) 考虑吸引势函数和安全势函数的作用。

2) 同时考虑吸引势函数、安全势函数和障碍物势函数的作用。

假设目标航天器在空间中处于无外力矩的自由旋转状态，且目标航天器不存在机动。其初始轨道根数如表1所示。

表1 目标航天器轨道根数

目标航天器的转动惯量Jt为

初始时刻目标航天器的姿态四元数qt(t0)和角速度ωt(t0)分别为

安全区的安全距离rs和安全走廊的安全角度θs分别为

追踪航天器的质量mc和各方向所能提供的最大推力Fmax分别为

吸引势函数的各参数分别为

安全势函数的各参数分别为

假设障碍物为半径3 m的球体，障碍物势函数的各参数分别为

需要说明的是，上述仿真参数的选择采用了尝试法，而没有进行最优化处理。仿真时间为200 s，仿真步长为0.05 s。

场景1考虑吸引势函数和安全势函数的作用，将式(44)中的Qo设为Qo=diag(0,0,0)，仿真结果如图4～图9所示。

图4 目标航天器的姿态与角速度

图4为无控旋转目标航天器的姿态和角速度变化曲线，由图4可以得出，不同时刻目标航天器的姿态和角速度各不相同。

图5为追踪航天器与目标航天器对接口的相对位置和相对速度变化曲线，经过110 s，追踪航天器到达了对接口位置，此时追踪航天器与对接口的相对速度为0 m/s，此后追踪航天器与对接口的相对位置和相对速度保持不变。

图6为位置角和参考位置角的变化曲线。经过69 s，方位角与参考方位角相同，并在之后两者保持同步。经过67 s，高低角与参考高低角相同，并在之后两者保持同步。

图5 追踪航天器与对接口的相对位置与相对速度(场景1)

图6 位置角与参考位置角(场景1)

图7为目标航天器体坐标系中追踪航天器与目标航天器对接口的相对运动变化曲线。图8为安全剖面图，由图7和图8可知，追踪航天器先逼近到目标航天器对接轴位置，之后沿着对接轴缓慢逼近追踪航天器，期间没有与安全区和安全走廊发生碰撞。

图7 目标航天器体坐标系中追踪航天器相对目标航天器运动(场景1)

图8 安全剖面(场景1)

图9为追踪航天器的控制加速度变化曲线，该控制加速度为追踪航天器视线坐标系描述的。由图9可以得知，为了跟上目标航天器对接口的位置，追踪航天器视线方向(x方向)始终需要提供控制加速度，该加速度在-0.2～0.2 m/s2之间来回切换。视线方向的加速度出现了严重的过饱和现象，说明发动机实际所能提供的控制加速度小于目标引力加速度，这主要是Qp和Ql取值较大决定的。如果Qp和Ql的取值较小，则目标引力加速度对位置误差和速度误差不敏感，导致追踪航天器的控制精度变差，甚至达不到预定的目标位置。初始时刻y方向和z方向控制加速度变化剧烈，经过72 s，y方向和z方向的控制加速度保持在一个极小的值，小于0.002 m/s2。本文中x方向开闭次数最高频率为20 Hz，而实际航天器冷气推力系统的开闭时间能够达到20 ms(频率50 Hz)，所以本文仿真结果(频率20 Hz)是可以实现的。

图9 控制加速度(场景1)

场景1说明，当考虑吸引势函数和安全势函数的作用时，混合势函数制导可以实现追踪航天器沿着安全路径对无控旋转目标的逼近，逼近过程中能够避免与目标航天器的附件发生碰撞，保证了安全性要求。

场景2在场景1中追踪航天器逼近目标航天器的运动路径上添加一个障碍物。同时考虑吸引势函数、安全势函数和障碍物势函数的作用，仿真结果如图10～图14所示。

图10 追踪航天器与对接口的相对位置与相对速度(场景2)

图11 位置角与参考位置角(场景2)

图12 目标航天器体坐标系下追踪航天器相对目标航天器对接口运动(场景2)

图13 安全剖面(场景2)

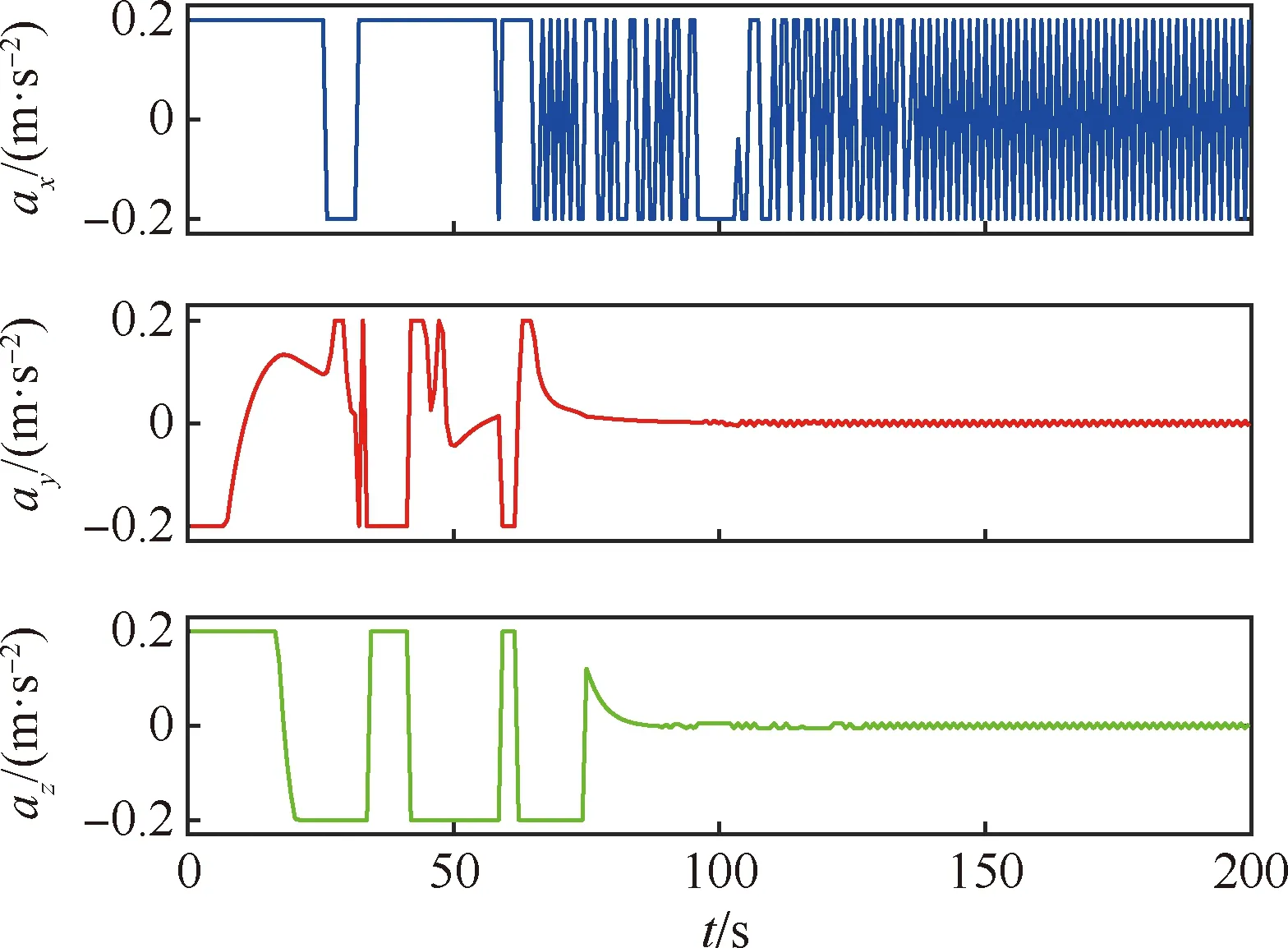
图14 控制加速度(场景2)

图10表明追踪航天器到达了目标航天器对接口的位置，与对接口的相对位置为0 m，相对速度为0 m/s。图11表明追踪航天器的位置角跟上了参考位置角。图12和图13表明，在考虑避障势函数作用时，追踪航天器能有效避开障碍物，最终安全逼近无控旋转目标。图14表明，经过一段时间，追踪航天器y方向和z方向的控制加速度趋向于0 m/s2，x方向的控制加速度在-0.2～0.2 m/s2之间来回变化。

场景2说明，当考虑障碍物势函数作用时，混合势函数制导可以使追踪航天器有效避开障碍物，实现追踪航天器沿着安全路径对无控旋转目标的逼近，保证了安全逼近和避障的制导要求。

表2给出了两种场景下的燃料消耗，由表2可知，场景2的燃耗比场景1的燃耗高，说明当追踪航天器需要躲避障碍物时，其所需燃料显著增加。

表2 不同场景所需燃料

4 结 论

研究了追踪航天器利用混合势函数对无控旋转目标航天器的安全逼近和躲避障碍物的制导问题。建立了追踪航天器相对于无控旋转目标航天器的相对运动方程。设计了吸引势函数、安全势函数和障碍物势函数。根据Lyapunov理论对混合势函数的稳定性进行了分析，并推导了追踪航天器的控制加速度。最后进行了数值仿真，仿真结果表明：

1) 当考虑吸引势函数和安全势函数的作用时，混合势函数制导可以实现追踪航天器沿着安全路径对无控旋转目标的逼近，逼近过程中能够避免与目标航天器的附件发生碰撞，保证了安全性要求。

2) 当同时考虑吸引势函数、安全势函数和障碍物势函数的作用时，混合势函数制导可以使追踪航天器有效避开障碍物，实现追踪航天器沿着安全路径对无控旋转目标的逼近，保证了安全逼近和避障的制导要求。

3) 当追踪航天器需要躲避障碍物时，其燃料消耗也更多。