基于布尔网络的语义悖论研究

陈智斌

（1.华南师范大学政治与行政学院，广州510631；2.广东技术师范大学计算机科学学院，广州510665）

0 引言

语义悖论（Semantic Paradox）是一种与计算机科学，特别是数理逻辑理论研究密切相关的逻辑悖论，这一点早已通过哥德尔不完全性定理及其对角线引理所揭示[1]。说谎者悖论是最为古老而典型的语义悖论，它可以用自然语言表达如下：

语句(L)为假 (L)

语义不稳定是语义悖论语句表现最为突出的现象。就以说谎者悖论为例，当对语句(L)赋值为真（假）时，它在下一阶段将为假（真），而在再下一阶段又变为真（假），如此反复。也就是说，说谎者语句(L)有悖于常理之处在于，无论如何赋值都无法断定(L)的真假。为此，需要回答以下问题：是什么导致了悖论语句的语义不稳定？

上述问题可借助计算工具加以讨论。已有一些学者尝试通过计算工具研究语义悖论的语义不稳定性[2]。然而，上述工作仅研究了说谎者悖论及其变体的语义不稳定现象，并没有一般性地探讨语义悖论的语义不稳定现象。为此，本文把研究范畴扩展到布尔悖论上。布尔悖论是语义悖论的一种子类型，说谎者悖论即属于布尔悖论。以下是一个关于布尔悖论的典型例子[3]：

从以上例子可见，布尔悖论的特点是其中每条语句均等价于一组语句的布尔组合，而每条语句的真值又取决于其他语句的真值。受此启发，本文发现布尔网络（Boolean Network）作为一种广泛应用在生物学、复杂系统研究中的数学模型[4]，与布尔悖论存在等价关系。因此，本文将通过引入布尔网络及其相关分析理论和计算工具，利用布尔悖论与布尔网络的等价性，在系统层面分析并研究布尔悖论的语义不稳定性，探究形成语义不稳定性背后的系统性因素。

1 布尔系统与布尔网络

1.1 布尔系统

这里主要研究带有真谓词的语义悖论（即真理论悖论），真谓词是指用于断定语句真假的谓词。例如前面举例提到的说谎者悖论，语句(L)断定了自身为假，因此其形式语言表达中应含有真谓词以及否定符号。在悖论研究中，布尔系统是指根据对角线引理构造的一组语句集。为给出布尔系统的定义，首先引入带真谓词的算术语言及相关概念。记N 是包含0 的自然数集，设L 为算术语言，N 是L 的标准结构，Th( )N 是L中的真算术理论。在L 中加入真谓词T 得到L+，设X是关于T 的解释，以N+X⊨A 表示A 在模型N+X 中为真并简记为X⊨A。L+的真算术理论Th+( )N 包含了所有满足如下条件的语句A：对任意X，有。为简化表示，使用X( A)=1 代替，使用X( A)=0代替N+X⊭A。给出有关定义如下：

定义1（布尔系统）[6]有穷语句集Δ={δi|1 ≤i ≤n}称为是一个布尔系统，如果对每个1 ≤i ≤n，都存在布尔组合式fi，使得：

在上述定义中，fi(p1,…,pn)是通常的命题公式，p1,…,pn是其中可能出现的命题变元。是在fi(p1,…,pn)中对p1,…,pn分别同时代入得到的语句。其中是语句δi的哥德尔编码表示该编码在L 中对应的数字，并且把形如的语句简记为。后面把fi称为一个布尔组合，同时它也代表对应的布尔函数（真值函数）。

定义3（修正周期）[6]设Δ 是语句集，X0⊆N。数m ≥1 称为是Δ 在X0上的修正周期（简称周期），如果存 在N ≥0，使 得 对 任 意k ≥N 和 任 意 A ∈Δ，Xk+m(A)=Xk(A)都成立。称m 是Δ 的一个周期，如果m是Δ 在某个X0上的周期。称除自身外不能被Δ 的其他周期整除的周期为Δ 的主周期。

给 定 布 尔 系 统Δ={δi|1 ≤i ≤n}和X0⊆N，称Xk(δ1)Xk(δ2)…Xk(δn)(k ≥0)为Δ 的一个真值排列。给定修 正 序 列，称 对Δ 的 真 值 排 列 按k=0,1,…排序而构成的序列为Δ 的一个修正序列。在文献[6]中已经证明，对任意X0⊆N，布尔系统在阶段k+1 的真值排列由阶段k 的真值排列决定，且按如下规则计算：

1.2 布尔网络与布尔系统的等价性

布尔网络是由N 个变量v1,…,vN构成的有向图，图中每个节点对应一个变量。每个变量均只有0 或1两种可能取值并由布尔函数fi:{0,1}ki→{0,1}决定，其中ki表示节点vi共有ki条输入边。布尔网络中各节点的输入边数目（入度）可以相同，也可以不同。往往规定各节点入度均为K，如果允许各节点入度不同，则取平均入度作为参数K[4]。布尔网络也称为N-K 模型。需要指出的是，为一般地研究布尔网络的特性，更常见的布尔网络模型是随机布尔网络，即给定节点数目及网络平均入度的取值范围，随机地选取网络样本，但在每个网络演化过程中网络拓扑和布尔组合不变。因此许多布尔网络的研究结论是在统计意义上成立。在一些文献中会更确切地使用“随机布尔网络”（Random Boolean Network）这样的术语。

布尔网络属于一种离散动力系统（Discrete Dynamical System），即按离散的时间点更新网络中各节点的状态。称排列v1(t)v2(t)…vN(t)是布尔网络在时刻t(t=0,1,…)的状态s(t)，其中vi(t)是vi在时刻t 的取值。称序列s(t )s( t+1) s( t+2 )…是布尔网络的一段演化轨迹（Trajectory）。布尔网络的演化规则如下，在每个离散时刻t+1，变量vi的取值vi(t+1)由在时刻t 的ki个输入决定：

比较式（2）和式（3）容易发现，布尔系统修正序列的真值排列计算规则与布尔网络的演化规则本质是相同的。对于具有n 条语句的布尔系统和具有N 个节点的 布 尔 网 络(n=N)，设X0(δ1)X0(δ2)…X0(δn)=v1(0)v2(0)…vN(0)，取相同的布尔组合fi（1 ≤i ≤n），对所有k=t，布尔系统在阶段k 的真值排列等同于布尔网络在时刻t 的状态。

定义4（等价性）称布尔系统Δ 和布尔网络Ω 是等价的，如果Δ 与Ω 使用同一组布尔组合 fi（1 ≤i ≤n）。

合肥市轨道交通1号线车站建筑方案设计的思路及探讨………………………………………………………… 闫阳（10-44）

1.3 布尔网络吸引子与语义稳定性

一旦布尔系统被表示为等价的布尔网络后，布尔网络动力学理论及工具就能为研究布尔系统的语义行为提供一条全新的途径。利用布尔网络的计算机模拟工具，能够获得任意布尔系统的语句真值变化过程。而且，根据布尔系统和布尔网络的等价性，两者的许多性质可以互相印证和使用。例如，记布尔网络所有可能状态构成的集合为S，则（N 是节点个数）。由于S 是有穷的且演化按式（3）进行因而是确定性的（Deterministic），因此布尔网络从任意初始状态出发演化都必然会有状态重复出现，使得网络的演化轨迹呈现周期性。布尔网络的周期性通过吸引子（Attractor）来表达，它是S 的一个非空子集，一旦网络演化到某个吸引子中的某一状态后，演化轨迹将按确定次序反复遍历吸引子内各状态。显然，一个布尔网络的吸引子长度（即吸引子中的网络状态数目）相当于布尔系统的一个周期。由以上讨论可知布尔网络至少有一个吸引子，换言之布尔系统至少有一个周期。而且由于S 是有穷的，显然布尔网络只存在有穷多个吸引子，对应地布尔系统只存在有穷个主周期。这一点同样已经在布尔系统的相关研究中被证明了[6]。

本文基于布尔网络的吸引子对布尔系统的语义稳定性定义如下。

定义5（语义稳定性）设布尔系统Δ 有等价的布尔网络Ω，Ω 的吸引子集合为A。对于a ∈A即为吸引子长度。划分Δ 的语义稳定性如下：

（2）称Δ 是语义不稳定的，如果存在a ∈A，|a |＞1。特别地，称Δ 是悖论的，如果对所有a ∈A，|a |＞1。

2 实验方法及结果

2.1 实验方法

本节将通过实验讨论在引言中提出的问题：是什么导致了悖论语句的语义不稳定？针对当前所要研究的对象，该问题可具体化为：为什么有的布尔系统是语义稳定的，但有的却是语义不稳定的？两类布尔系统之间在什么方面存在差异？

首先，利用归一化汉明距离（Hamming Distance）函数能够计算布尔系统的两条真值排列的差异程度，而真值排列的差异程度即反映了悖论语句集的语义不稳定性。根据按前面所给的布尔网络定义，归一化汉明距离函数可表示如下：

根据上述汉明距离函数定义布尔系统的语义不稳定度。然后利用布尔系统与布尔网络的等价关系，可对用于分析布尔网络动力学特性的德里达曲线（Derrida curves）[7]方法加以改造。具体定义如下：

定义6（语义不稳定度）设布尔系统Δ 有等价的布尔网络Ω，Ω 的吸引子集合为A。对每个a ∈A，设a={s1,…,sm}且s1s2…sm是Ω 的一段演化轨迹。称是a 的周长，其中H 是归一化汉明距离函数。Δ 的语义不稳定度为Ω 所有吸引子的周长之和。

定义7（德里达曲线）设布尔系统Δ 有等价的布尔网络Ω。在时刻t 任取Ω 的一个状态s(t)，有ρ(t)=H(s(t),s(t+1))和ρ( t+1)=H( s( t +1),s( t+2 ))，其 中H 是归一化汉明距离函数。称(ρ(t),ρ( t+1))为Δ 的德里达曲线上的一个点。

定义7 实际是把布尔系统的一段包含有3 个阶段的修正序列转换为德里达曲线中的一个点。在这段修正序列中，ρ(t)表示了布尔系统从时刻t 到t+1 有多少语句的真值发生变化，ρ( )t+1 则表示了这些变化在再下一阶段给系统造成多大的后续变化。因此，布尔系统的德里达曲线反映了其语句真值变化的传递特性。本文称布尔系统中语句真值变化的传递特性为它的系统稳定性。下面通过实验分析系统稳定性对布尔系统的语义不稳定性的影响。

2.2 实验结果

本实验通过在MATLAB 软件上编写程序（使用了http://www.teuscher.ch/rbntoolbox/提供的工具箱），随机构造布尔系统作为统计样本并将它们按语义稳定性分类。实验中分别从节点个数N=10,12 的布尔网络中各随机选取了1000 个样本，它们的平均入度K 取值范围均为1～5。假设已得到若干个具有相同语义稳定性的布尔系统，根据定义7 可随机地抽取这组布尔系统的德里达曲线上的点并将抽取结果合并，由此得到具有某种语义稳定性的布尔系统的德里达曲线，统计结果如图1 所示。

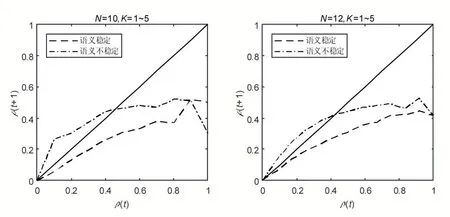
图1 语义稳定和不稳定的布尔系统的德里达曲线

从图1 可见到，在统计意义上语义不稳定的布尔系统的德里达曲线基本位于语义稳定的布尔系统对应曲线的上方，这表明任意时刻在语句真值变化程度相同的情况下，与语义稳定的布尔系统相比，语义不稳定的布尔系统会在下一时刻引致更多语句的真值发生变化。也就是说，对于语义不稳定的布尔系统，它的系统稳定性较低，而对于语义稳定的布尔系统，它的系统稳定性较高。而且，语义不稳定的布尔系统有一部分曲线位于图中对角线（即直线ρ(t+1)=ρ(t)）的上方且与对角线相交于原点外的另一点。因此从统计意义上来看，此类系统在演化过程中ρ(t)将收敛于该交点，使得系统中语句真值持续地变化下去，从而形成了语义不稳定的现象。与此相反，对于语义稳定的布尔系统，曲线在图中对角线的下方并只与对角线交于原点，因此语句真值变化所带来的影响会被逐渐消减为零。

表1 从实验样本集抽取了五个典型例子，由表中结果可见，系统稳定性越低的布尔系统，其语义不稳定度越大。这一结论与图1 的统计结果相一致，表明系统稳定性，即布尔系统中语句真值变化的传递特性对于语义稳定性所起的作用。

表1 一些布尔系统实例

3 结语

为探究语义悖论的语义不稳定现象，本文利用布尔网络的计算工具及分析理论通过计算实验探讨了布尔悖论语义不稳定的系统性因素。实验结果表明，对于系统稳定性较低的布尔系统，语句真值的变化通过语句间网络关系一直传递下去，从而形成了语义不稳定现象。进一步，可利用本文所介绍的工具和方法研究语义悖论的自指性。