基于贝叶斯粗糙集的肺部肿瘤CT图像抗噪算法设计*

卓德强

(武汉大学中南医院放射科 ， 湖北 武汉 430071)

1 引 言

近年来，癌症患者死亡率逐年递增，肺癌的死亡率远高于其它癌症[1-2]。CT图像作为胸部影像学中最常用的图像，大范围应用于肺部肿瘤检测中[3-4]。医生通过CT影像观察分析患者病情，作出正确的病情判断[5]。在此过程中，医生的诊断能力会影响诊断精准度，肺部肿瘤CT图像的质量更是影响临床诊断结果的关键[6]。尤其在传输过程中，肿瘤CT图像受到各种噪声干扰，图像质量下降，图像细节以及纹理特征信息缺失[7-8]，会严重干扰图像的观察与分析结果，易导致误诊[9-10]。因此，去除肺部肿瘤CT图像噪声、保留图像细节以及纹理特征信息的研究具有重要的意义[11]。

粗糙集通过决策规则实现分类能力，可对不确定决策系统进行分析及约简，获取合理的决策规则[12]，在图像数据分析方面具有优越性。本研究拟设计一种基于贝叶斯粗糙集的肺部肿瘤CT图像抗噪算法，对取得的肺部CT图像进行分类，利用贝叶斯粗糙集构建分类模型，判断肺部CT图像中是否存在肿瘤；对存在肿瘤的肺部图像进行去噪处理，基于分类结果构建小波系数拉普拉斯数学模型，取得小波系数的预估值，采取贝叶斯MAP估计方法得到小波系数的概率密度，实现肺部肿瘤图像自适应抗噪处理。

2 数据和方法

2.1 数据来源

2.2 方法

2.2.1基于贝叶斯粗糙集约简的肺部肿瘤CT图像分类 约简决策规则，预测肺部CT图像类别，将图像以是否存在肿瘤划分成两类。

此贝叶斯粗糙集模型基于经典粗糙集分类模型构建，采用先验概率替换变精度粗糙集中的参数β，提升其噪声数据处理能力，用于处理决策表不协调分类问题。

决策规则约简是根据决策逻辑将决策算法中各决策规则的非必要条件过滤，针对每一项决策规则过滤掉冗余属性值[14]。每一条决策规则均从第一个属性开始依次减少，并核实减少该属性是否会造成决策表失衡，失衡则继续保留。以此类推，实现所有决策规则约简[15]。利用约简生成的全部决策规则构建肺部CT图像分类模型，获取分类对象和决策规则间的匹配度后，求取决策类别相同规则匹配度之和，将此类别规则数量作为除数，求取两者之商，商值大的规则决定图像类别，以此预测肺部CT图像中是否存在肿瘤。

2.2.2去噪方法 将拉普拉斯分布作为小波系数的数学分布模型，基于贝叶斯最大后验概率估计小波系数，对存在肿瘤的肺部CT图像进行抗噪处理。

(1)肺部肿瘤CT图像的拉普拉斯数学模型

设定g为受到噪声污染的肺部肿瘤CT观测图像，g=b+ε，其中b为真实的干净图像，ε为服从N(0,θ2)分布的加性高斯噪声，针对g实施小波变换可得y=w+n，其中y是观测肺部肿瘤CT图像，w是真实肺部肿瘤CT图像，n是噪声所对应的小波系数，n亦服从N(0,θ2)的分布。估计贝叶斯是在g中最大限度的恢复b的相近预估值b′，实际图像实施小波变换之后，全部子带的小波系数均在0时处于峰值，两边有长拖尾，使整体看起来是一种尖峰形状，体现小波系数具备长拖尾性。拉普拉斯分布模型可准确表示肺部肿瘤CT图像的相关统计性能。拉普拉斯模型仅具备一个参数，计算量相对较小[16]，数学表达式简单明了，遵循图像分布特性，能够较好获取小波系数的预估值[17]，拉普拉斯模型概率密度函数表达式见式(1)：

(1)

其中，θx表示边缘标准差。

(2)贝叶斯最大后验概率估计

(2)

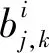
(3)

其中P()、L[ ]分别为概率密度函数、代价函数，代价函数用式(4)表示：

(4)

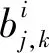
(5)

式(5)可简化为式(6)：

(6)

依据贝叶斯定理获取式(7)：

(7)

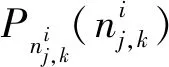
(8)

(9)

(3)贝叶斯自适应去噪算法

为使贝叶斯算法具自适应性，需把每个小波系数视为具备不同边缘标准差(局部相关随机变量)的拉普拉斯分布[18]。噪声方差能良好体现噪声统计特性，对噪声方差做大限度估计，估计方法见式(10)：

θn=Mediany((i))/ξ(i)

(10)

(11)

其中，Q为邻域中小波系数个数。

(12)

基于贝叶斯自适应去噪算法步骤：首先对肺部CT图像实施小波变换，并估算噪声方差；其次计算子带小波系数标准差，基于通过多次传输，噪声较少，画面清晰；为原始肺部肿瘤CT图像添加高斯噪声，见图1(b)，作为图像抗噪声处理的对象；图1(c)、图1(d)、图1(e)、图1(f)分别是式(9)概率密度得到真实图像小波系数的MAP估值，对MAP估计值实施小波反变换，完成肺部肿瘤CT图像去噪。

3 结果

图1(a)为肺部肿瘤CT原始图像，且未经均值滤波结果、中值滤波结果、小波阈值结果以及本研究算法去噪结果；表1是不同噪声标准差下图像抗噪信噪比。

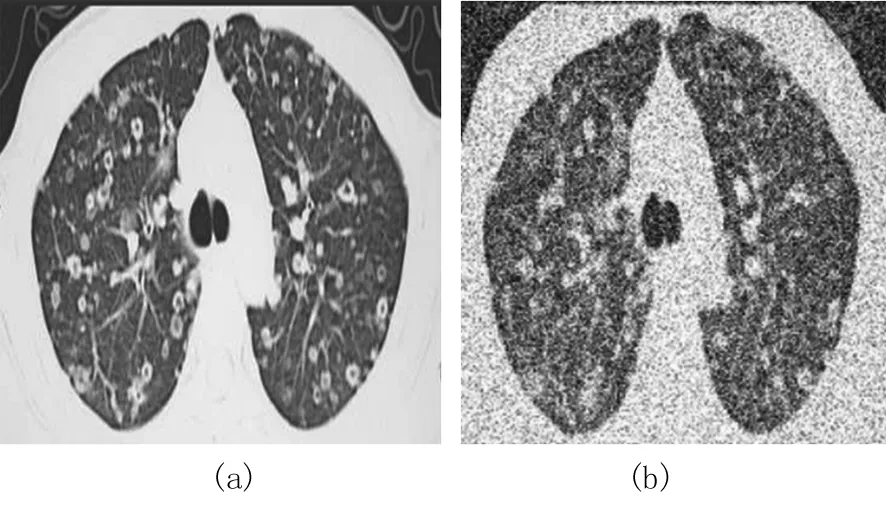
图1 四种抗噪算法的图片视觉效果图(a).原始图像;(b).加入噪声的图像;(c).均值滤波结果;(d).中值滤波结果;(e).小波阈值结果;(f).本研究算法结果Fig.1 Visual effects of 4 anti-noise algorithms表1 不同噪声标准差下四种算法图像抗噪信噪比Table 1 Image anti-noise SNR of four algorithms under different noise standard deviations

噪声标准差加噪图像抗噪处理后的峰值信噪比/%均值滤波中值滤波小波阈值本研究算法522.8187 24.421528.128030.40481022.727824.061726.387528.02601522.608023.410326.063727.91222022.510723.041424.332526.46052522.458022.866324.152125.54803022.055622.106422.810023.66043522.010122.028422.6558 22.93054021.000421.070421.274721.8607

通过分析图1和表1可知，以上四种算法对添加噪声的实验图像均能实现去噪，但图像视觉效果差别很大，均值滤波算法的视觉效果最差，并且在不同噪声标准差上的峰值信噪比均处于最低值，中值滤波算法、小波阈值结果算法结果相似，图像噪声处理效果差、处理后图像峰值信噪比较低；本研究算法在不同噪声标准差上的峰值信噪比最高，且去噪处理后的图像和原始图像接近，说明采用本算法进行抗噪处理的图像视觉效果更好，抗噪性能更优。

四种算法处理不同类型噪声结果见表2。

表2 四种算法处理不同类型噪声结果Table 2 Fouralgorithms for processing different typesof noise results

由表2数据可以看出，均值滤波算法对三种类型噪声的抗噪效果最差，小波阈值算法在处理椒盐噪声时效果低于中值滤波算法，对其它两种类型的噪声抗噪效果较好，本研究算法针对三种噪声的抗噪效果最优，在四种算法中具有显著优势，因此本算法针对不同噪声均具有良好抗噪效果。

4 结论

本研究设计一种基于贝叶斯粗糙集的肺部肿瘤CT图像抗噪算法，基于贝叶斯粗糙集进行图像分类，相比经典贝粗糙集分类模型而言，具有较强噪声数据处理能力，应用在CT噪声图像分类中，得到的图像分类结果精度较高，为后期进行肺部肿瘤CT图像去噪提供有利条件，降低图像去噪难度。