基于扩展卡尔曼滤波的磁共振指纹参数量化优化算法*

2019-10-30黄敏张璐坚周到陈军波

生物医学工程研究 2019年3期

黄敏，张璐坚，周到，陈军波

(中南民族大学生物医学工程学院，武汉 430074)

1 引言

磁共振成像(MRI)技术已被广泛应用于临床检查，但MRI一次扫描只能得到T1、T2或质子密度中的一种加权像，对医生的经验要求较高。2013年,Griswold等人提出了“磁共振指纹”(magnetic resonance fingerprinting,MRF)成像方法[1]，可通过一次扫描，得到多参数的定量图像。

经典MRF成像框架需要建立一个包含被扫描部位所有组织的参数信息的字典,字典大小与参数匹配的准确度和效率密切相关。该框架存在匹配时间过长，字典不具有通用性等缺陷。基于分组匹配方法[2]和奇异值分解(SVD)[3-4]后再匹配的方法可以加快匹配速度。基于压缩感知[5-6]的方法可加速匹配过程，提高准确度，但对不同的采样序列，当改变TR和FA后，需重新生成字典，增加了额外的时间和空间成本。

目前提出的基于无字典的MRF参数量化框架的方法中，有采用深度学习得到参数图像，代替基于字典的匹配过程[7-8]，但深度学习需要大量数据作为训练支撑，可获得的MRF采集数据和标签数据非常少。Zhang等人提出了使用卡尔曼滤波的方式对参数进行量化，无需训练数据，但量化时间较长[9-10]。为此，我们研究了基于扩展卡尔曼滤波的磁共振指纹参数量化方法，并对量化速度和精度进行了优化。

2 参数量化方法

MRF技术采用伪随机变化的TR和FA组合(如1 000组)进行扫描，获得对量化参数敏感的独特信号。为缩短扫描时间，在每组TR时间内，可采用单支螺旋轨迹采样，得到K空间欠采样数据。对采样数据进行逆NUFFT得到空间域图像，将空间域图像各点对应位置的多帧信号连接起来，即得到每个体素的“磁共振指纹”信号。在经典MRF参数量化中，需要根据所有组织参数组合与序列参数，通过Bloch方程建立字典库。将指纹与字典信号进行逐条匹配，通过匹配结果得到参数像。

卡尔曼滤波(KF)可用于线性系统的信号跟踪和观测，是一种最优估计方法[11]。而利用扩展卡尔曼滤波(EKF)，可实现对非线性系统(MRF属于此类)的优化估计问题。我们先建立磁共振指纹成像模型；对模型的MRF信号进行EKF跟踪观测，使估计值趋近于真实值，实现对该信号的输入参数进行反推和估计。该方法简称为EKF-MRF方法。

2.1 模型建立

在MRF中，磁场不是绝对均匀的，存在偏振频率df。若k时刻某组织的磁化矢量信号为Mk=[Mxk;Myk;Mzk], 待量化的参数组合为pk=[T1;T2;df]，定义此时的联合状态向量为：

Xk=[Mk;pk]=[Mxk;Myk;Mzk;T1;T2;df]

(1)

将MRF数据演变过程看作一个非线性系统，系统动态方程可以表示为：

Xk=f[k-1,Xk-1]+wk

(2)

Zk=h[k,Xk]+vk

(3)

其中Zk为观测值，wk∈R6×1为过程噪声(近似高斯白噪声)，其协方差为Qk。vk∈R2×1为观测噪声，其协方差为Rk。

由MRF原理可知，f(*)为非线性变换，h(*)为线性变换。k时刻的测量值[Mxk;Myk]与系统变量之间是线性关系，观测矩阵H表示为：

(4)

若采用bSSFP序列[1]进行MRF数据采集，根据Bloch方程，k时刻的系统变量与k-1时刻的系统变量之间是一个复杂的非线性关系。

已知k-1时刻的磁化矢量Mk-1，结合组织参数pk，要计算出下一时刻的磁化矢量Mk，需要经过三步：

(1)首先，经过dt1时间的自由进动后，磁化矢量可通过Bloch方程计算，即：

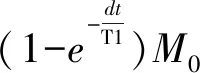
(5)

其中，ω为偏振角频率，dt为当前信号采集时刻到下次射频施加之前的时间段dt1(bSSFP序列为0.5TR(k-1))。得到自由进动状态下磁化矢量：

Mt+dt=g(Mt,dt)

(6)

可另写为：

M1,k=g(Mk-1,dt1)

(7)

(2)施加下一RF脉冲后(翻转角为αk，相位为0和180°相互交替的φk)，得到新的磁化矢量：

(8)

其中，

(9)

(3)再经过dt2时间的自由进动，按照式(2)计算新的磁化矢量Mk。其中，dt为下次射频施加时刻到下次信号采集时刻的时间段dt2(bSSFP序列为0.5TR(k))，可表示为：

Mk=g(M2,k,dt2)

(10)

由于每个体素的组织参数T1，T2和磁场不均度df是不变的。将磁化矢量与参数相结合，可得到k时刻的联合状态变量Xk。最终公式为：

Xk=f(Xk-1)=

(11)

2.2 参数量化

基于扩展卡尔曼滤波的MRF参数量化过程，主要是对五个关键方程进行迭代计算：

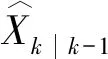
(12)

(2)预测协方差矩阵Pk|k-1

Pk|k-1=FkPk-1|k-1FkT+Q

(13)

(3)求解卡尔曼增益Kk

Kk=Pk|k-1HT(HPk|k-1HT+R)

(14)

(4)状态更新X(k|k)

(15)

(5)协方差更新Pk|k

Pk|k=(I-KkH)Pk|k-1

(16)

其中，f(Xk-1)为EKF-MRF的非线性状态方程。将k-1时刻状态变量代入式(11)，得到k时刻状态的估计值。

通过状态方程的一阶线性化得到转移矩阵，由于状态向量Xk含有[Mk;pk]两部分，所以最终状态转移矩阵为：

(17)

随机输入待量化的三个参数T1，T2和df的初始值，通过扩展卡尔曼滤波不断跟踪预测信号，对方差进行估计，更新参数组合的值,最终使参数组合通过状态方程后，得到的信号趋近于信号真实值。说明此时参数值已趋近于组织真实值，即得到了量化结果。

2.3 EKF-MRF优化

为减少MRF扫描时间，使用500组TR和FA的脉冲序列进行数据采集，但经过500次卡尔曼迭代后，未能得到收敛的参数值，需要对观测值进行数据复制。

通过实验发现，过程噪声Q和观测噪声R对实验结果的准确性影响较大，Q值直接迭代次数。在第一轮(500次)EKF迭代时，由于初始参数值是随机的，计算的预测值偏离真实值较远，我们选取较大的Q值，使卡尔曼运算中更偏向测量值。在第一轮卡尔曼迭代过程中，各参数值向真实值迅速趋近，但不能精确收敛。当参数值已经趋近于真实值后(误差变小)，再将Q值逐步调小，使其收敛在一个固定值附近。

实验表明：当R值过小，收敛后量化的T1,T2参数值会较真实值偏小；当R值过大，各参数将不能准确收敛。经过大量试验后，我们将卡尔曼滤波算法中的数据重复次数控制在四轮，即2 000个点处，可以得到逼近真实值的量化结果。

相较于Zhang等人的方法[10]，本研究还在状态方程的一阶线性化过程中做了优化。前者在一阶线性化过程中将状态方程分成两个非线性方程和一个线性方程，做了两次一阶线性化过程。我们基于EKF原理，将状态方程作为一个整体仅做一次一阶线性化，计算速度大大加快。

3 实现与结果

3.1 单组织参数量化结果

翻转角FA采用添加了柏林噪声的伪随机变化值，并加入随机噪声；TR取范围为6.5～14 ms的随机值，见图1。模拟脑部组织参数值，在df为4 Hz，SNR为15 dB条件下，对EKF-MRF方法进行实现和分析。

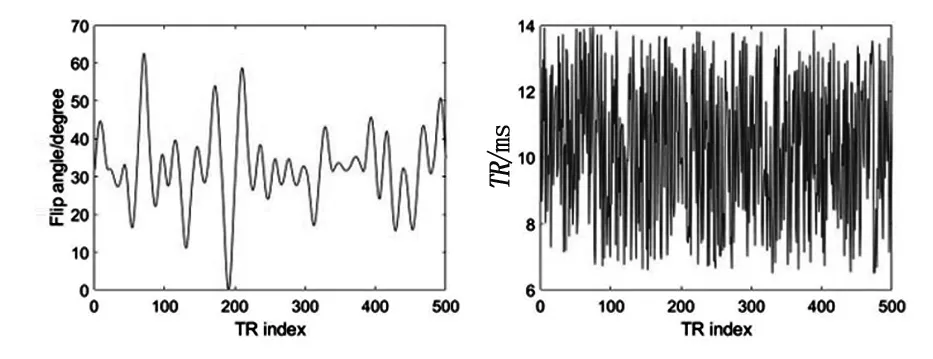
图1 翻转角与重复时间Fig.1 Flip angle and repetition time

选取T1=500 ms，T2=70 ms，df=6 Hz，分析观测噪声和测量噪声对实验结果的影响，见图2。图2(a)中，当R值偏小时，df虽然能收敛，但收敛值偏小；(b)中，当R值偏大时，df不能收敛；(c)中，当Q值固定时，df在较大范围内震荡，不能准确的收敛；(d)为本研究的df结果，能较快并准确的收敛。

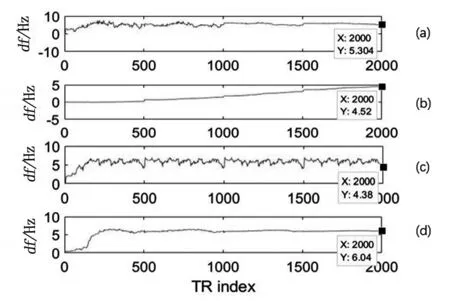
图2 噪声对结果的影响Fig.2 Influence of noise on results

选取T1值最高的脑脊液(T1∶2 569 ms、T2∶329 ms)，以及T1值与T2值差距最大的肌肉(T1∶350 ms、T2∶70 ms)进行实验，得到仿真的磁化矢量Mx和My，见图3。

脑脊液和肌肉的参数估计值收敛曲线见图4。测量数据在重复1轮至1 000个点时，估计值已收敛到较小范围；到1 500个点时，能得到稳定收敛且误差很小的参数值，证明优化方法可得到逼近真实值的参数估计值。

图3两种组织的磁化矢量

Fig.3Magnetic vector of two tissues

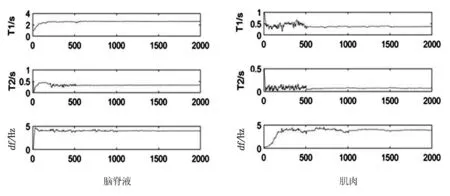
图4参数估计曲线

Fig.4Curves of parameter estimation

3.2 二维模型结果

在配置为Intel Core(TM) i5-8300H 2.30 GHz 的PC上，在Matlab R2017b环境下，对上述算法进行实现。

为了将EKF-MRF优化法与Zhang等人的方法[10]进行比较，使用相同的BrainWeb数据库中人脑模型进行仿真。BrainWeb的模型大小为217×181×181，将每层扩充为256×256，在1T条件下，设置每层组织的T1、T2以及质子密度值[4]。模拟信号采集的SNR为15 dB，df在范围为0～12 Hz内呈指数趋势中心对称变化，并对非感兴趣区域添加掩膜。

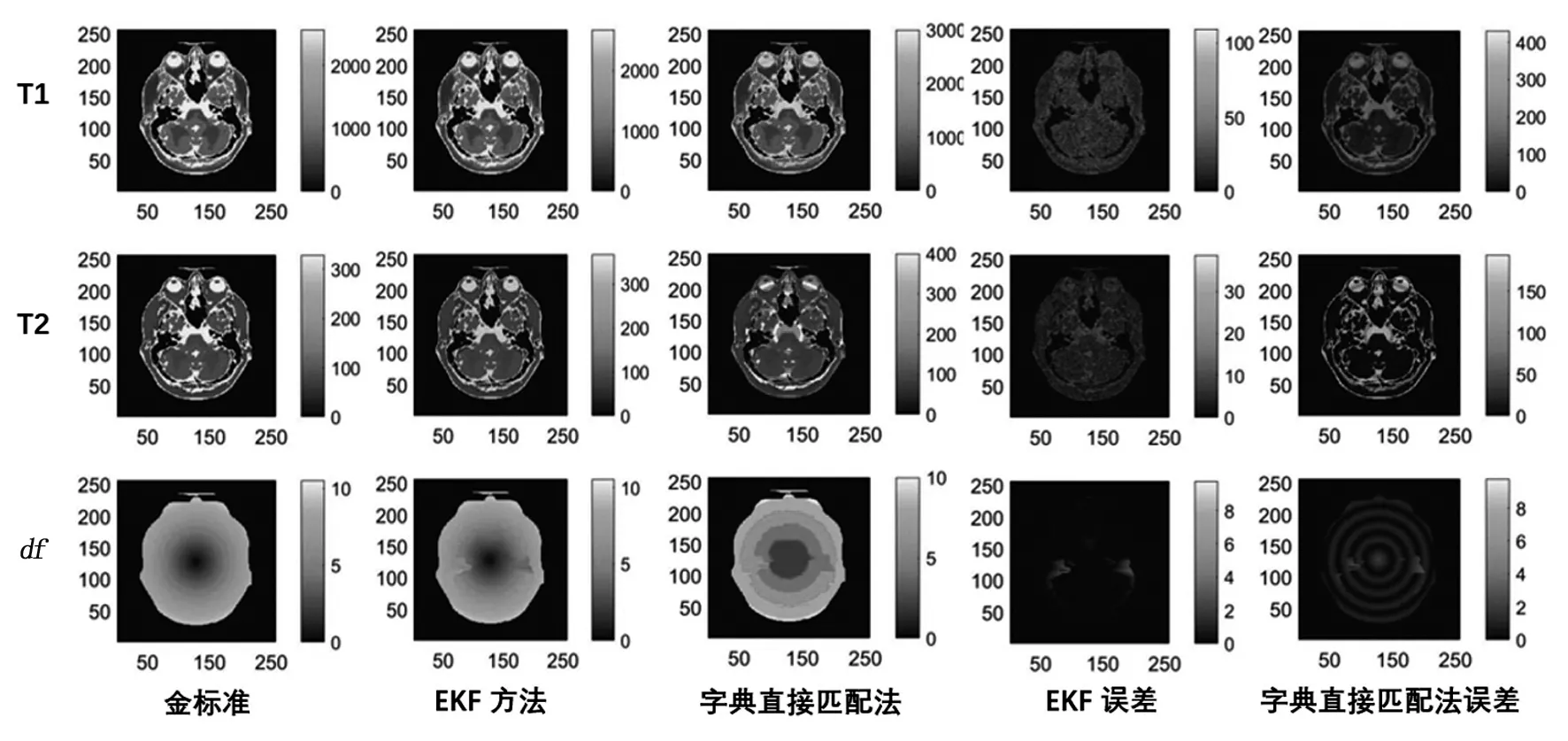
另外，为了与字典量化法比较，我们建立了字典。参数选择：T1值范围为100～5 000 ms(100～2 000 ms之间，以20 ms为间隔；2 000 ms以上，300 ms为间隔)；T2范围为20～3 000 ms(20～100 ms之间，以5 ms为间隔；100～200 ms之间，以10 ms为间隔；200 ms以上，200 ms为间隔)；df范围为-20～20 Hz(2 Hz为间隔)；得到字典入口数为91 266个。由组织特性可知，无T1

EKF-MRF及字典法的参数量化图像见图5，匹配误差及量化时间见表1。准确度采用参数量化结果与金标准之间的均方根误差作为衡量标准。

结果表明，EKF-MRF法在量化的准确度和效率上均优于字典直接匹配法。直接匹配法的最大缺陷是T2量化图失真严重，df量化出现环状伪影。EKF-MRF法T2量化精度明显增强，误差明显缩小，df量化无环状伪影。

表1 匹配误差及量化时间Table1 Matching error and quantification time

Zhang等人的方法[10]，对BrainWeb数据进行64×64点量化，用时42 min；可估算该方法量化256×256点的图像需要640 min。本研究的优化方法，参数量化256×256点仅需约38 min，时间缩短了1个数量级，效率明显提高。提高的关键在于：对测试数据的重复次数仅需要4次即可达到迭代的精度要求；雅克比矩阵仅用直接一次性计算，大大节省了时间。

为进一步测试量化的准确度，三个参数组合中保持两个不变，观测对剩余一个参数的量化影响。在T2=60 ms和df=6 Hz时，分析T1量化的准确性；在T1=600 ms和df=6 Hz时，分析T2量化的准确性；在T1=600 ms和T2=60 ms时，分析df量化的准确性。结果见图6，表明EKF-MRF在T1,T2,df具有很好的量化效果。字典直接匹配法T1参数估计较准确，df估计误差较大，T2误差尤其大。