引入二次方项的NSS模型实证研究

2019-10-30陶浪平

山西财政税务专科学校学报 2019年2期

陶浪平林江

(安徽财经大学，安徽蚌埠 233030)

利率是金融市场中一个十分重要的指标，在过去的很多年中，不管是理论学者还是金融机构的管理人员都对其十分重视。由于不同期限的利率一般有所不同，由此引出的利率期限结构问题成为人们关注的焦点。利率期限结构又称到期收益率曲线，指的是无违约风险下利率与不同到期期限的一一对应关系。由于国债一般没有违约的风险，学术界常将国债的收益率曲线看成一个国家的利率期限结构。

在资源的配置过程中，利率的市场化是一种有效的方式。自1996年我国逐步推进市场化改革以来，利率市场化程度稳步提高。在经历了20多年的发展后，央行对于利率的管制一步步放松，现在主要存在于存款的上限和贷款的下限中。2012年，央行扩大了金融机构存贷款利率的区间。2013年底，央行推出的银行同业存单业务意味着松动了大额存款利率。2014年3月1日，人行开放上海自贸区的小额外币存款上限，意味着自贸区内实现了外币利率市场化。2015年10月24日起，央行不再对金融机构设置存款利率浮动上限，实现了利率管制的基本开放。对于利率市场化，有专家给出观点：由于可能出现的区域性套利问题，我国应该加强全国利率市场化建设；与此同时，伴随着互联网金融的快速崛起，各种网贷平台强势发展，利率市场化的速度应该加快。因此，在这个大环境下，研究利率期限结构就显得十分必要。

由于利率曲线的形状、利率水平的高低、长短期利率的利差等因素，利率期限结构隐含着大量的信息。国内外对于利率期限结构的研究主要分为两个角度：静态利率期限结构和动态利率期限结构。对于静态的利率期限结构模型，常见的有B样条模型、指数样条模型、多项式样条模型、NS族模型等。本文的研究主要是建立在NSS模型上，于经典的NSS模型中引入二次方项，建立了一个扩展的NSS模型,并使用二次移动平均法进行动态预测。

一、文献综述

国内外对于静态利率期限结构模型的研究是比较多的。国外对于NSS模型的研究要追溯到1987年Nelson和Siegel提出的一种较为简单的收益率曲线模型。Nelson和Siegel(1987)从动态利率期限结构模型中推导出指数形态的瞬时远期利率，并通过即期利率与瞬时远期利率的关系推导出即期利率函数，该模型就是NSS模型的基础——NS模型。Svensson(1994)在NS模型的基础上进行扩展，添加了一个新的曲度项，这就是著名的NSS模型。Bjork和Christensen(1999)在 NS 模型的基础上也新增了一个项，但不同的是该项是用于描述斜率特征的因子。Diebold和Li(2006)将时间序列引入NS模型，构建了时变的NS模型。

随着我国利率市场化改革进程的不断推进，国内学术界对于以NSS为代表的NS族模型的研究在近些年开始增多。朱世武、陈建恒(2003)对比了多项式样条模型和Svensson模型对上交所国债利率期限结构拟合的结果，认为NSS模型在收益率曲线的短端拟合能力优于多项式样条模型，不过在收益率曲线的远端，NSS模型的效果并不很好。谈正达、霍良安(2012)通过构建无套利的NS模型对中国国债市场进行分析，认为无套利的NS模型拟合能力比NS模型更好，并且无套利的NS模型样本外预测能力很好。文忠桥(2013)通过对NS模型的参数构建AR(2)过程进行预测，发现样本内的预测结果较为理想，但是样本外的不理想。丁志国等(2014)使用NS族模型对中国国债收益率数据进行拟合，认为NS族模型之所以拟合效果较好，是因为模型中的潜在因子能够较好地刻画收益率曲线关于宏观经济变量变化的预期。丁志国等(2014)利用NS模型对利率期限结构和宏观经济因素之间的关系进行实证判别，认为宏观经济因素对利率期限结构影响明显，但是并不稳定，其影响的结果取决于人们对于经济形势的预期。赵晶等(2014)基于2005年至2014年9月国债市场月度数据，对比了NS模型和NSS模型的拟合效果，发现NS模型能够更好地拟合中国国债的利率期限结构特征。沈根祥、陈映洲(2015)在NS模型上引入第二个斜率因子，构造了双斜率因子的模型，增强了收益率曲线的静态拟合及动态预测能力。王雪标、赵前程(2017)考察了银行间债券期限结构模型估计，发现系数估计中存在显著的小样本偏差，然后利用Bootstrap模拟的偏差修正方法进行修正，重新解释了我国远期利率及远期溢价的一些重要特征。

二、理论与模型简介

(一)传统的利率期限结构理论

虽然不同到期期限的利率变动并不是完全相关的，但是其中的高度相关性引起人们的关注。那么究竟是哪些因素导致了利率期限结构的变化呢？这些因素中哪些是主导因素呢？学者们通过主成分和因子分析给出了数学和统计角度的解释,然而这些解释过于数学模型化，因此，给出其经济意义就显得十分重要。

利率期限结构理论主要有四个：纯预期理论、流动性偏好理论、市场分割理论、期限偏好理论。

1.纯预期理论。纯预期理论认为当前的利率期限结构表示了市场对未来即期利率变化的预期。该理论给出了不同形状的收益率曲线与未来即期利率变化的关系，即收益率曲线和未来即期利率的变化是同涨同跌的。

2.流动性偏好理论。流动性偏好理论是建立在纯预期理论上的，该理论认为债券的剩余期限越长，流动性风险越高。由于市场中大多数投资者都是要规避风险的，因此，只有当长期债券的收益率同时含有预期利率水平和流动性风险溢价时，投资者才可能会增持长期债券。流动性偏好理论对于不同形状的利率期限结构有较好的解释能力，如对于收益率曲线上升的问题，该理论认为有两种可能的原因：第一，市场对于未来的利率预期是上升的；第二，利率预期水平不变或者有一些轻微的下降，但是流动性风险溢价随着期限的增加而增加的幅度很大，不仅能抵消利率预期的下降，还能使其上升。

3.市场分割理论。市场分割理论认为不同的投资者有各自不同的期限偏好，并且期限不变。由于大量的投资者根据自身的需求将债券的到期期限与个人的投资计划进行匹配，导致债券市场不再是一个整体。当不同的债券市场处于完全分割状态时，交易发生于相互分离的市场中，某一个期限债券价格的变动不影响投资者对其他期限债券的需求。

4.期限偏好理论。期限偏好理论是建立在市场分割理论的基础上的。该理论认为由于不同投资者本身的资产及债务状况有很大差异，因此各投资者有着特定的投资期限偏好，并且各种特定投资偏好是变动的。例如，当不同到期期限的债券供求发生较大变动时，风险溢价与利率风险失衡，投资者的偏好就会发生变化。

对以上四种理论进行对比总结可以发现：纯预期理论最为基础，该理论的核心是未来即期利率变化的预期；流动性偏好理论则在预期理论的基础上引入了流动性风险溢价；市场分割理论则是站在另一个角度进行分析，认为投资者有各自不变的期限偏好；而期限偏好理论则在流动性偏好理论的基础上，认为投资者的期限偏好是会随着供求因素的变动而变动的。

(二)粒子群算法简介

本文在对模型待估参数进行估计时，使用了经典的粒子群算法。粒子群算法简称PSO，是进化算法的一种。该方法的主要思想是从随机解出发，通过反复迭代寻找最优解，主要内容如下：

在一个D维的目标空间中，有N个粒子组成的一个群落，其中第i个粒子表示为一个D维向量：

Xi=(Xi1，Xi2，…，XiD)，i=1，2，…，N

(1)

第i个粒子移动的速度也是一个D维向量：

Vi=(Vi1，Vi2，…，ViD)，i=1，2，…，N

(2)

第i个粒子迄今为止搜索的最优位置为个体极值：

Pbest=(Pi1，Pi2，…，PiD)，i=1，2，…，N

(3)

整个粒子群迄今为止搜索的最优位置为全局极值：

Gbest=(Pg1，Pg2，…，PgD)，g=1，2，...，N

(4)

在搜索这两个极值时，粒子根据式(5)、式(6)来不断调整自己所在的位置以及相应速度：

(5)

(6)

其中,c1，c2是学习因子，r1，r2为均匀随机数。

式(5)由三部分组成：第一部分称为惯性，表示粒子本身的运动趋势；第二部分是认知部分，表示粒子有向自身历史最佳位置运动的趋势；第三部分是社会部分，反映粒子有向群体最佳位置逼近的趋势。

(三)NS族模型简介

NS族模型中最为基础的就是NS模型，在该模型的基础上，又延伸出NSS模型、BC模型和DL模型。

1.NS模型。NS模型全称是Nelson-Siegel模型，是Nelson 和 Siegel在1987年提出的。该模型的瞬时远期利率是指数形式的：

ft(τ)=β1+β2e-λ1τ+β3λ1τe-λ1τ

(7)

由此推导出t时刻到期收益率函数为:

(8)

其中，参数β1刻画了长期的利率变动水平，因此被定义为长期因子。参数β2被称为短期因子，因为其因子载荷项是一个从1开始迅速衰减为0的函数。参数β3是曲度因子，因为该因子的载荷项先从0开始逐渐增大，等增大到一定程度后又开始衰减，直至减为0。这样的变化过程很好地描述了中期因子的变化趋势，因此曲度因子又被称为中期因子。λ1表示的是指数衰减率，NS模型可以通过最小二乘法估计β1、β2、β3三个参数的结果。从该模型可以看出，模型的设计非常简便，而且三个参数的含义十分明确，很多研究者使用NS模型对利率期限结构进行拟合，均取得了较好的效果，因此，NS族其他模型均是对NS模型的补充和改进。

2.NSS模型。NSS模型又称Svensson模型，是NS模型的一种重要的扩展型。该模型在NS的基础上增加了一个曲度因子。这样的改进使模型的中期因子更加灵活多变，适用更多形状的收益率曲线，增强了模型的拟合能力。该模型的具体表达式如下：

ft(τ)=β1+β2e-λ1τ+β3λ1τe-λ1τ+β4λ2τe-λ2τ

(9)

(10)

λ2是该模型在NS基础上新增的衰减因子。

3.BC模型。BC模型和NSS模型类似，也是在NS的基础上增加了一个因子。与NSS模型不同的是，BC模型增加的是斜率因子，并且这个增加的斜率因子拥有更快的衰减速率(2λ)。该模型的具体表达式如下：

ft(τ)=β1+β2e-λ1τ+β3λ1τe-λ1τ+β4e-2λ1τ

(11)

(12)

4.DL模型。DL模型是NS模型的又一个扩展模型，该模型将时间序列引入NS模型，构建了时变的模型变量，该模型的具体形式如下：

ft(τ)=β1t+β2te-λ1tτ+β3tλ1tτe-λ1tτ

(13)

(14)

本文所构建的二次方项NSS模型则是建立在NSS模型基础上的，是NSS模型的一种扩展形式。该模型t时刻到期收益率yt(τ)具体表现形式如下：

(15)

三、实证分析

(一)数据选取说明

由于我国国债市场主要由证券所交易市场和银行间交易市场组成，而我国的金融机构仍然以银行为主体，并且银行间市场国债交易量巨大，在整个国债市场占有很重要的地位，因此本文选择的数据是银行间国债市场利率日交易数据。数据的时间跨度是从2017年1月6日至2018年12月30日，数据来源于万德数据库。

本文之所以选择日交易数据是因为日交易数据量非常大，能够较为精确地对债券市场的收益率曲线进行拟合。除去非交易日、部分缺失值以及异常值后，样本的交易天数为471天。对模型参数进行估计的指标有五个：收盘价、每年付息次数、票面利率、剩余期限和收盘价的修正久期。由于每日的平均交易数据有几百个，每个交易数据都由上述五个指标的数据组成，因此整个原始面板数据量达到38万。

(二)扩展的NSS模型估计结果分析

本文在NSS模型的基础上引入了二次方项，通过使用MATLAB软件进行编程，对收益率曲线的五个参数β1、β2、β3、β4、β5进行估计。在这里，我们通过对不同时间参数进行拟合比对，将两个时间参数进行固定。我们给出了五个参数的描述性统计，如表1所示。

表1 收益率曲线参数描述性统计

从表1可以看出，几个参数的标准差都比较小，中位数和最大值、最小值差距不大，这说明模型参数整体较为稳定。从峰度和偏度两个指标来看，五个参数整体上离群程度较低，但是β2和β3两个参数相对于其他三个参数的数据离群程度较高。表2、图1给出了用MATLAB运行的2018年11月2日的到期收益率结果及相应的收益率曲线图。

表2 2018年11月2日的到期收益率数据

从图1的收益率曲线图可以看出，随着到期期限的增加，利率随之增加，其中在前8年时间内，到期收益率的增长是非常迅猛的。10年期限以上的收益率虽然整体也在上涨，但是涨幅明显放缓。对2017年1月至2018年12月的数据重复上述操作，得到每日的收益率曲线。将每日的数据进行汇总并计算出各到期收益率，我们通过表3的描述统计表和图2的三维图展示结果。

图1 2018年11月2日的收益率曲线

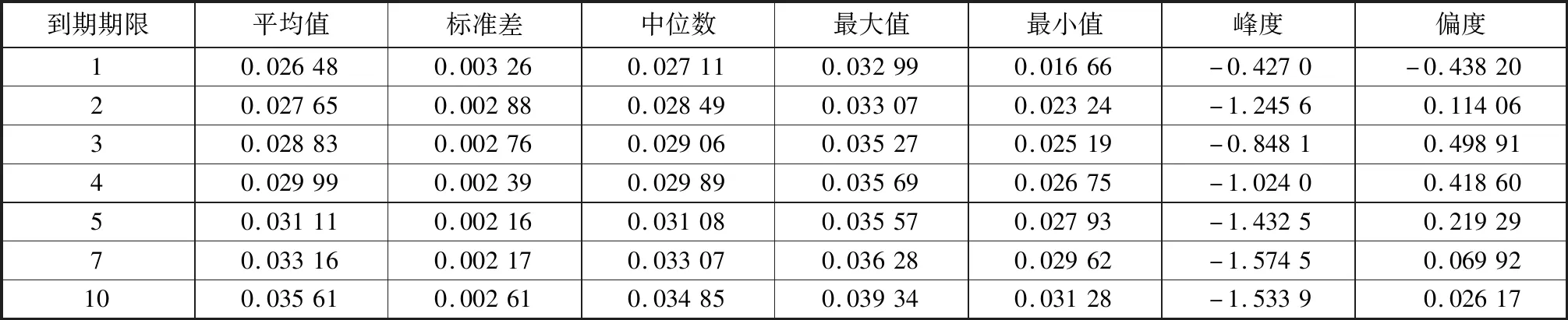
表3 各到期期限利率的描述统计结果

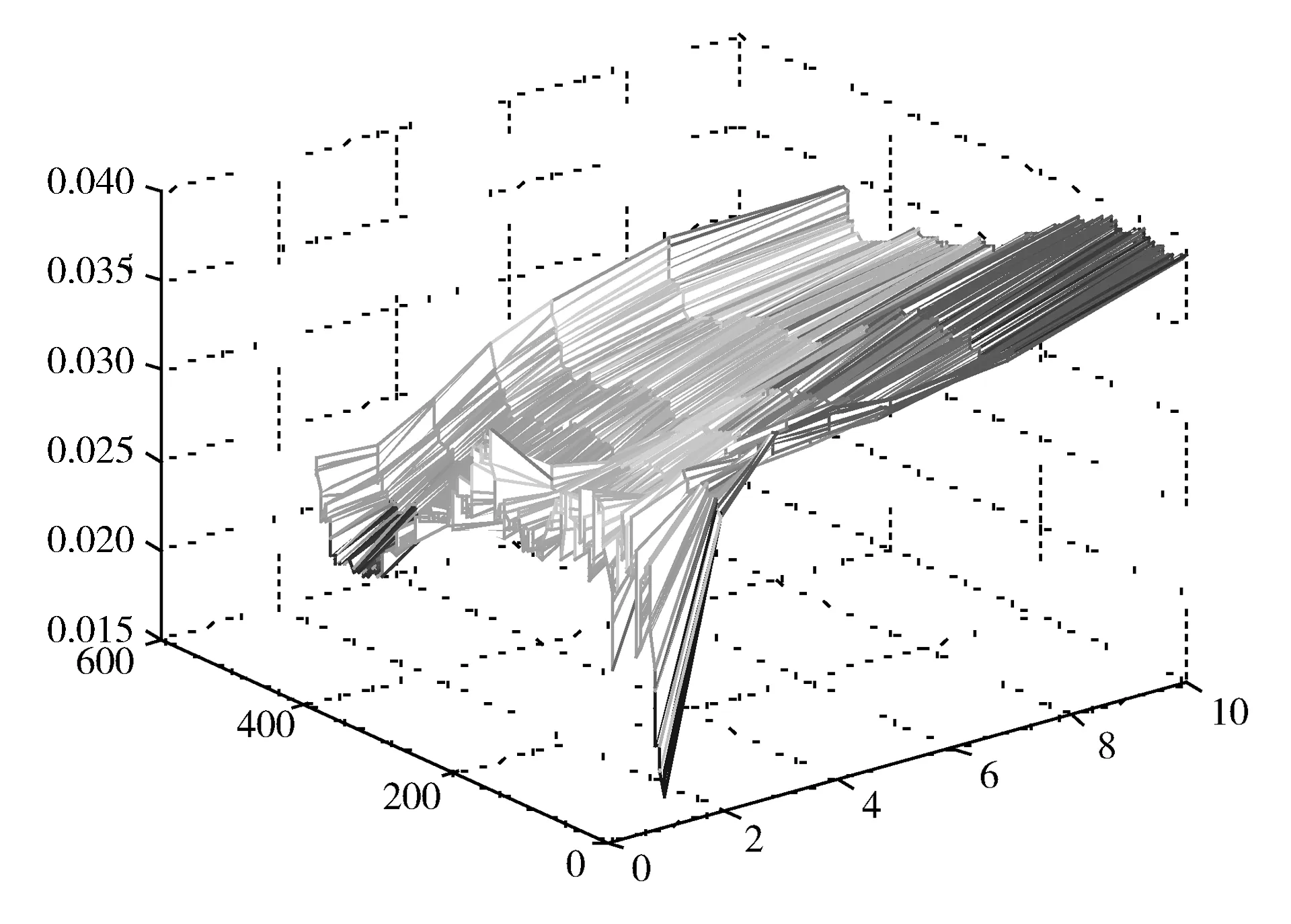
图2 2017年1月至2018年12月利率期限结构三维图

表3和图2分别给出了不同到期期限利率的描述统计汇总和2017、2018两年的利率期限结构走势。图2清晰地展示了利率期限结构的整体变动趋势。随着剩余年限的不断增加，到期收益率不断上升，并且上升的幅度在短期较大，而在长期则逐渐减小。这个现象的发生从流动性偏好理论的角度进行解释是由于风险溢价的存在。随着年限的增加，投资者所面临的不确定性也在增加，为了弥补这种由时间跨度增加而导致的不确定性，投资者往往会要求更高的投资收益率。表3则给出了到期收益率数据的各统计指标。首先，从均值、中位数、最大值和最小值的变动趋势可以看出，随着年限的增加，数据整体增大，这和利率期限结构的三维图是一致的。其次，从标准差可以看出，各期限的到期收益率均非常平稳。最后，峰度和偏度的两组值总体上较小，这说明数据的离群程度较低，实验的结果较为理想。

(三)模型的样本内预测

我们用建立好的模型对2017年(样本总量为36 534)、2018年(样本总量为40 551)银行间债券价格进行样本内预测，误差结果如表4、表5所示。

表4 2017年绝对误差

表5 2018年绝对误差

表4、表5给出了2017年和2018年银行间市场债券价格的样本内预测误差。由2017年的绝对误差值我们可以发现，误差小于1的个数为19 041，总体占比达到52%，误差小于2的个数达到25 438，总体占比将近70%，误差高于10的总体占比为2%。由2018年的数据可以发现误差小于5的个数有33 455，总体占比为83%，误差在10以上的个数仅占5%。因此，从总体看，引入二次方项的NSS模型样本内预测的结果是比较理想的。