区域管制扇区复杂性指标构建及分析

董襄宁 胡明华 李孝荣

（1.南京航空航天大学国家空管飞行流量管理技术重点实验室，南京，211106；2.中国国际工程咨询有限公司，北京，100048）

引 言

随着飞行流量不断增长，空域承受压力日益加大。为缓解和平衡压力，空域被划分为若干扇区。相比进近管制扇区，区域管制扇区范围更广，航空器虽速度更快但滞空时间更久，管制员同时管辖的航空器数量更多，且航路阶段对航空器引导限制较进近阶段更严格，因而区域管制员调配冲突手段更少。针对区域管制扇区特征，构建复杂性指标集，以真实扇区数据为样本，分析指标相关性，探寻指标相互影响规律，将为扇区复杂性研究提供实证。

空中交通管制复杂性被定义为两个维度，一是静态扇区特征（扇区复杂性），二是动态交通流模式（交通复杂性）[1]。扇区复杂性作为空中交通管制复杂性研究的重要分支，广受关注。丛玮等[2]将扇区复杂性表征为结构复杂性和运行复杂性两类，探讨了扇区复杂性指标体系的评估方法。王红勇等[3]用冲突解脱指数来建立航空器间的内禀复杂度计算模型，设计了空域复杂度的可视化表示方式。高伟等[4]构建了扇区静态复杂度和动态复杂度，并对比了区域管制扇区与进近管制扇区复杂度差异。Sunil等[5]发现区域管制空域中对空域内水平方向路径进行过度结构化约束将导致空域容量下降。Popescu等[6]提出空域如果提供更灵活的路径将有助于降低管制员的工作负荷。许炎等[7]基于雷达数据研究交通流参数内在影响规律，揭示了空中交通拥堵机理。

已有研究尚欠缺复杂性指标的相关性分析，难以明确复杂性指标相互影响规律，扇区样本或来自仿真而非真实扇区，或虽以真实扇区为对象但样本数量偏少。本文根据区域管制扇区结构与流量分布特征，构建复杂性指标集，以中国37个区域管制扇区数据为样本，分析指标相关性。

1 问题描述与复杂性指标构建

1.1 区域管制扇区结构特征

区域管制空域内的飞行活动为巡航阶段飞行，包括高空和中低空的航路航线飞行。典型的区域管制扇区如图1所示。图1中：区域管制扇区水平边界为a～f六个点联结的封闭凸多边形；r1～r5表示5条路径；进出点间有的是双向都有路径，如r1和r2分别往返于a，c两点；有的是仅单向有路径，如r3，r4和r5分别表示a飞往e，e飞往b和f飞往d的路径。区域管制扇区中航空器多为平飞，按照东单西双（即真航线角0°～179°使用单数高度层，180°～359°使用双数高度层）的高度层配备，因而r1和r2路径上各自平飞的航空器没有对头冲突。从路径交叉的情况来看，r1和r2分别与r4交于u和u′，r3与r5交于v，r4与r5交于w。其中，u和u′位置较近，可简化为一个交叉点。因此，图1计3个交叉点。由于区域管制扇区中航空器平飞比例大于高度改变飞行比例，因而交叉点附近的汇聚冲突成为区域管制扇区的主要飞行矛盾，扇区路径和交叉点数量成为度量其复杂性的两个重要指标。

此外，扇区的水平范围包括周长及面积的大小也会影响扇区的复杂性[8]。中国区域管制扇区包括中低空扇区和高空扇区，中低空扇区垂直范围一般是过渡高度层以上直至7800 m或8400 m，高空扇区垂直范围一般是8100 m或8900 m以上直至巡航高度层上限。调研发现，为平衡管制员工作负荷，各区域管制扇区的可用飞行高度层的数量大致相同。因此，本文不考虑区域管制扇区间的垂直范围差异。

1.2 扇区流量分布统计

有些扇区各路径流量分布较为均匀，而有些扇区流量则主要集中在其中若干条路径上。扇区内流量在不同路径的分布是否均匀也将影响扇区复杂性[9]。因此，有必要统计扇区典型繁忙日总流量在各路径的分布比例。考虑到各扇区路径数量不同，为便于比较，将统计比例进行先排序后累加。首先将统计的扇区内各路径流量占日流量比例从高向低排序，然后累加。当累加值刚刚超过某个限定值时，记录累加值及对应的路径数量。本文选70%为限定值，即各路径流量比例累加刚刚超过70%的值及其对应的路径数量。这反映了扇区内主要流量在不同路径上分布情况均匀与否。当然也可取60%，80%或其他值。

1.3 区域管制扇区复杂性指标建立

根据区域管制扇区的静态和动态特点，即扇区结构和流量分布的特征，表1定义7个区域管制扇区的复杂性指标。

表1 区域管制扇区复杂性指标定义Tab.1 Definitions of complexity indicators in area control sector

表1中，指标Acc1～Acc5定义比较直观，指标Acc6描述的是扇区流量分布的均匀水平，即数值越大，扇区流量在各路径上分布越均匀；指标Acc7描述的是扇区流量分布的不均匀水平，即数值越大，扇区流量在各路径上分布越不均匀。

2 分析算法

2.1 算法思路

首先统计各扇区的复杂性指标，对其极值、中位数、均值和变异系数进行计算分析，然后构建协方差矩阵分析指标间线性相关性，最后运用最短距离法确定指标间聚类关系。

2.2 相关性分析

设q个扇区样本，定义n个复杂性指标X1,X2,…,Xn，n×q矩阵表示为

式中xij为指标i在扇区j的值。指标i在q个扇区的均值表示为

方差表示为

由于每个指标量纲各不相同，需要将初始指标值标准化，以标准化的代替式(1)中xij，得到指标i的向量为

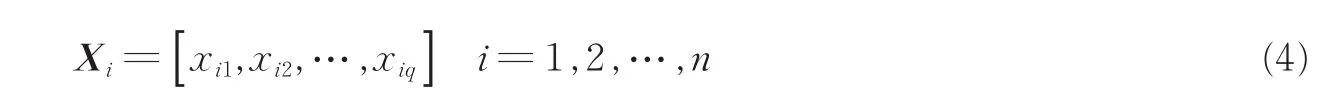
原始数据矩阵X的协方差矩阵R表示为

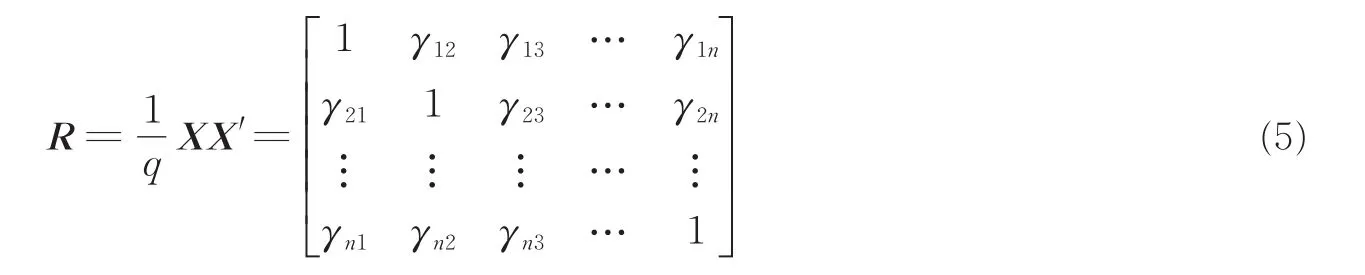
各指标的相关矩阵是主对角均为1的对称矩阵，即相关系数γij=γji。

2.3 聚类分析

先将每个指标各自分为一类，然后将距离最近的类合并成一个新类（简称并类），计算新类与其他类之间的距离，重复进行两个最近类的合并，每次减少一类，直至所有的指标合并为一类，形成聚类树图。

设类G包括n个指标，用行向量Xi(i=1,2,…,n)来表示，dij表示指标Xi与Xj间的欧式距离，DKL表示类GK和GL之间的距离。类间距离取最短距离，如式(6)所示。

若某一步类GK与类GL聚成一个新类，记为GM，类GM与任意已有类GJ之间的最短距离为

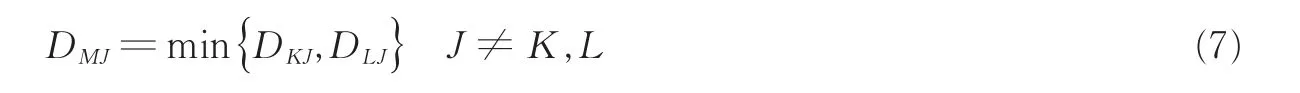
计算步骤如下：

(1)将初始的指标预处理成协方差矩阵，各自作为一类，计算n个指标的距离矩阵D(0)；

(2)寻找D(0)中最小元素DKL，将GK和GL聚成一个新类，记为GM，即

(3)计算新类GM与任一类GJ之间最短距离的递推公式为

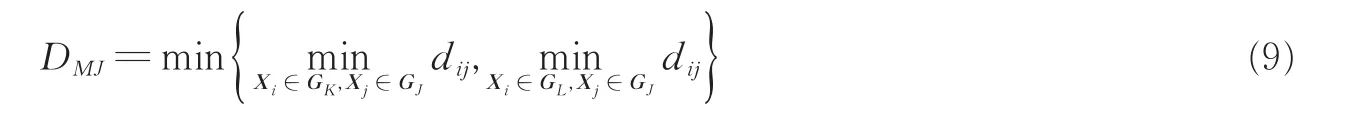
将GK和GL所在的行和列合并成为一个新行新列，对应GM，新行和新列上的新距离由式(9)计算，其余行列上的值不变，得到的新距离矩阵记为D(1)；

(4)对D(1)重复上述对D(0)的操作，得到距离矩阵D(2)。如此下去，直至所有元素合并为一类为止。

3 计算与结果分析

3.1 数据样本

本文选取区域管制扇区样本共计37个，分别隶属于中国东北、华东、西南、华南和新疆地区，具有较为广泛的地域代表性。数据采集日期分布在2011—2013年间，时段较为集中，具有一定的同期可比性。表2列出了37个区域管制扇区编号、名称和采样日期。

3.2 扇区复杂性指标描述性分析

样本扇区复杂性指标值的差异分析结果见表3。

表3中，只有指标Acc7的变异系数9.02%小于10%，离散程度较小，说明样本区域管制扇区流量在不同路径上分布的不均匀程度较为接近。其余指标变异系数均较大，如Acc4变异系数高达194.75%，说明中国区域管制扇区面积差异较大，如乌鲁木齐03扇区面积最大，是面积最小的广州02扇区的84.9倍。比较均值和中位数发现，除Acc3和Acc4外其余指标均值均接近中位数，也验证了样本扇区的范围差异较大。

表2 区域管制扇区样本Tab.2 Samples of area control sector

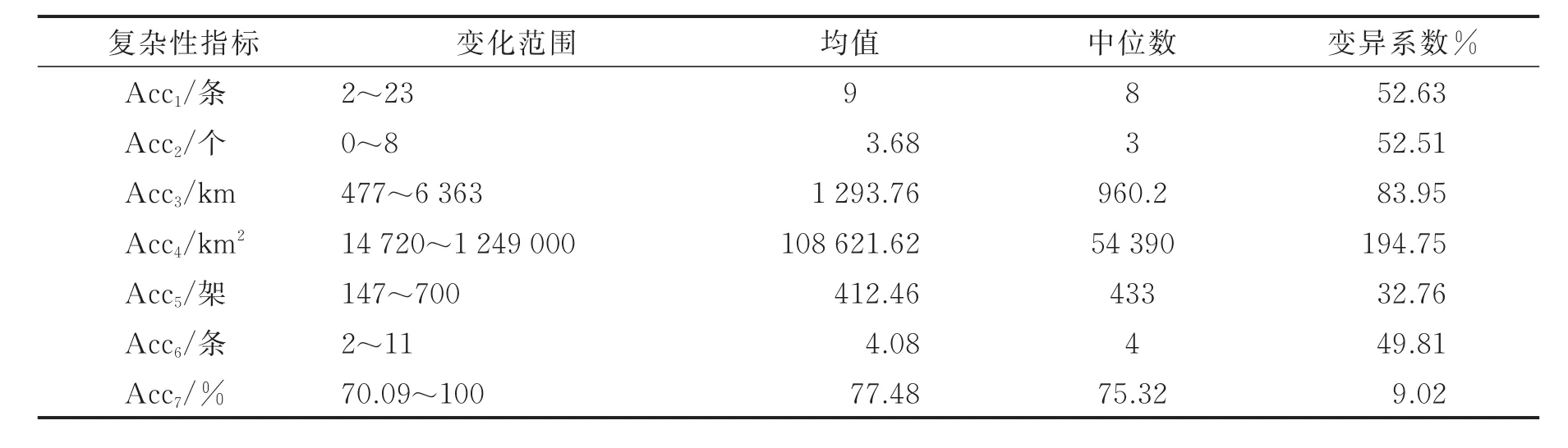
表3 区域管制扇区复杂性指标描述性统计Tab.3 Descriptive statistics of complexity indicators in area control sectors

3.3 协方差矩阵

考虑到区域管制扇区7个指标种类不一且量纲差异较大，对扇区数据标准化之后，求出其协方差矩阵如图2所示。图2的可视化协方差矩阵直观描述了7个指标的线性相关性，为一个对称矩阵。协方差取值范围为-1（含）～1（含）之间。数值为0表示不存在线性相关，数值为1（-1）表示线性正（负）相关。椭圆的颜色深浅与形状直观地描述了指标间的相关性。颜色越浅（或深），表示指标间正（或负）相关性越强。椭圆越扁（或圆），表示相关性越强（或弱）。椭圆顶部右（或左）倾表示相关性为正（或负）。

例如，路径数Acc1与交叉点数Acc2的相关系数是0.36，表明两者正相关，因为路径数越多，交叉点数也应越多；路径数Acc1与扇区范围（周长Acc3和面积Acc4）正相关（相关系数0.58/0.55）；周长Acc3与面积Acc4强正相关（相关系数0.96）；扇区范围（周长Acc3和面积Acc4）与扇区流量分布均匀程度（超70%路径数Acc6）正相关（相关系数0.54/0.59），与扇区流量分布不均匀程度（超70%流量比例Acc7）弱负相关（相关系数-0.06/-0.13），这说明范围大的扇区与范围小的扇区相比，各路径流量分布要更均匀些；日流量Acc5与扇区的范围（周长Acc3和面积Acc4）负相关（相关系数-0.36/-0.32），这说明扇区的范围越大，反而流量越低，这是因为流量增长将导致管制员工作负荷增加，达到一定阈值后必然会影响扇区安全，因此，随着流量的增长，该扇区将被划分为若干范围较小的扇区，即流量增长会导致扇区面积变小。注意到Acc6与Acc7除了与日流量Acc5分别弱负相关和负相关（相关系数-0.08/-0.46）外，与其他指标的相关系数均为相反数，前者说明流量分布不均匀的扇区往往日流量不大，但偶有例外，这表明为提升扇区服务能力，应尽可能均匀交通流的时空分布，但某些扇区会有例外；后者验证Acc6与Acc7这两个指标在绝大多数情况下能够反映扇区流量在不同路径上分布均匀与否。图2中7个指标两两间相关系数共计21个，例如交叉点数Acc2与扇区流量分布均匀程度（超70%路径数Acc6）正相关，但不存在因果关系。限于篇幅，没有因果关系的相关系数不再赘述。

图2 区域管制扇区复杂性指标的协方差矩阵Fig.2 Covariance matrix of area control sector complexity indicators

3.4 聚类树图

运用最短距离法对图2的协方差矩阵进行系统聚类，得到区域管制扇区7个复杂性指标的关系图谱（聚类树图）如图3所示。图3横坐标为并类距离（无量纲），纵坐标列出区域管制扇区复杂性指标，各指标自左向右的合并顺序反映了各指标被聚入新类的顺序。并类距离越近，说明指标间关系越紧密，聚类分6步完成。观察图3，发现以下3点特征：

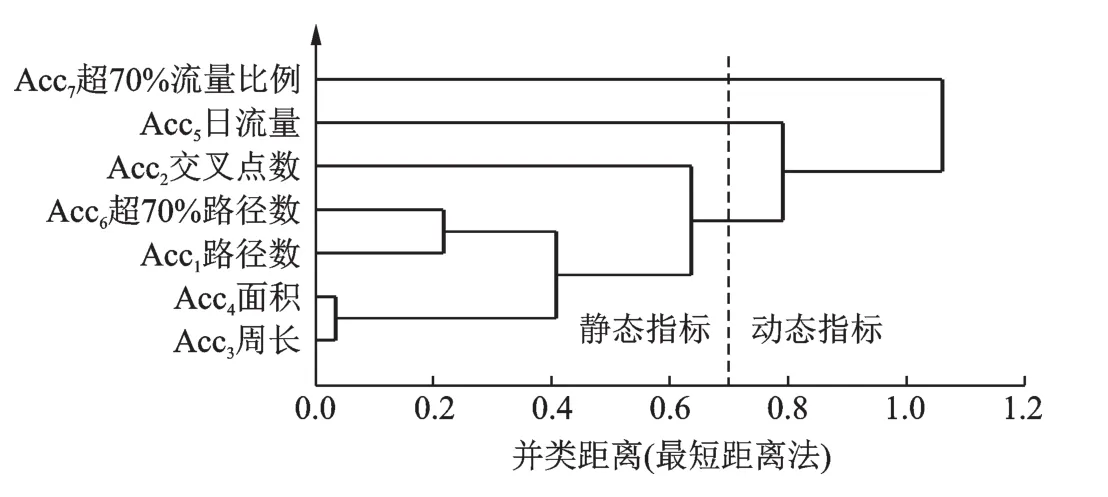
图3 最短距离法聚类树Fig.3 Single linkage method clustering tree

(1)描述扇区范围的面积与周长指标关系最近，第1步聚类就被合并；第2步将描述扇区流量分布均匀程度的超70%路径数指标与路径数指标合并；第3步将前两步聚类合并；第4步将第3步聚类与交叉点数指标合并。

(2)第5步将第4步聚类与日流量指标合并；第6步将第5步聚类与超70%流量比例指标合并，聚类完成。

(3)从聚类的顺序上看，以并类距离0.70为界，前4步聚类的指标都是偏重描述扇区静态特征的指标，后2步聚类的指标都是描述扇区动态特征的指标。这揭示了对于区域管制扇区，静态复杂性指标的共性强于动态复杂性指标。

4 结束语

本文首先分析了区域管制扇区结构和流量分布特征，构建了复杂性指标集。以中国37个区域管制扇区的复杂性指标为样本，研究了复杂性指标间的相关性，运用最短距离法，对区域扇区的7个复杂性指标进行聚类分析。基于样本，得到如下结论：

(1)区域各扇区面积相差悬殊（变异系数194.75%），但流量在不同路径的分布均匀程度比较一致（变异系数9.02%）；

(2)为提升扇区服务能力，应尽可能均匀交通流的时空分布，但对于某些扇区会有例外；

(3)扇区范围越大，往往流量在各路径上的分布越均匀（相关系数0.54～0.59），但扇区流量反而越低（相关系数-0.06～-0.13）；

(4)以并类距离0.70为界，扇区复杂性指标分为静态和动态两类，且静态指标共性强于动态指标。

本文选取集中在2011—2013年的37个扇区数据作为样本，经过多年的发展，各扇区流量分布和结构数据都可能发生改变。使用更新或更多的数据样本得到的分析结果可能会有变化，但基于扇区特征构建的复杂性指标及分析方法仍适用于样本变化的情况。