基于层次结构数据的多元线性回归问题分析
2019-10-30唐旭清
赵 芸 唐旭清,2
(1.江南大学理学院,无锡,214122;2.无锡市生物计算工程技术研究中心,无锡,214122)
引 言
线性回归(Linear regression,LR)分析或多元线性回归(Multiple linear regression,MLR)分析[1-3]主要用于研究变量间的相关关系及基于数据变量间客观规律的获取。作为一种常用的统计分析方法,MLR在实际问题研究中得到了广泛应用[4-7],同时理论也得到不断丰富和发展[3-8]。
近年来,随着计算机科学和网络技术的飞速发展,大批量数据不断涌现,大数据已经成为许多部门与行业一个重要的特点[9-11]。受实际需求影响,在大数据存储、计算过程中数据量庞大,一般多采用拓扑结构形式进行存储,其中较为常见的就是层次结构[12-13]。层次结构作为一种常用的数据结构,具有典型的树状特点,有利于存储数据的管理与检索。如银行、保险、医疗等行业的数据按行政区划就具有层次结构的特点,并且这些行业需要利用大数据处理技术进行不同地区间或者不同行业间的数据整合与分析。因此,基于层次结构的数据处理与计算技术研究就显得尤其重要和紧迫[13-14]。
随着大数据研究的不断深入,基于大数据的MLR模型被广泛应用于数据处理中。王慧文等[15]提出了MLR模型的增量算法,该算法可在已知全部数据信息的前提下,节约数据读取时间,减小了数据存储传输的压力。此外对于不同的回归分析模型,如Logistic回归也渐渐被引入大数据处理,并产生了相应的算法,Jiang等[16]提出了基于网络分布式数据的Logistic回归分析算法,用于数据间的规律获取。这些基于大数据处理与计算方法的探索与研究有利于提高计算的效率,同时对于具有层次结构的数据进行处理与计算时,除考虑现有问题外,更需要解决各层之间的联系以及数据综合的问题,如各分层部分的MLR系数与总的MLR系数的数量计算关系。除此之外,在一些特殊行业中,例如金融服务、医疗卫生等领域还面临着数据安全和隐私保护的问题,并已经成为大数据研究的重要问题之一。冯登国等[17]从宏观方面提出了大数据安全与隐私保护的一些构想。罗永龙等[18]提出了一种基于安全协议的隐私保护方法,并应用MLR分析方法进行研究。美国加州大学圣地亚哥分校的Jiang教授团队就分布式数据提出了隐私保护协议的支持向量机算法[19-20]。
在以上研究的基础上,本文提出了层次结构数据的MLR分析方法的研究,其主要目的是通过下层数据的部分偏回归系数以及层次结构矩阵来求解上层模型的偏回归系数,以此来实现由部分偏回归系数来构建全体MLR模型的目标。针对下层每个部分的偏回归系数,数据用户只需要提供原数据总和、平方和以及交叉项乘积和即可求解该部分的MLR模型的偏回归系数。与直接利用原始数据求解偏回归系数的相比,通过原数据总和、平均值以及交叉项乘积和的输入进行偏回归系数的求解,既可以保证原始数据的私密性,又可达到与原始数据直接输入相同的结果。同时模型可实现整个计算的并行处理,提高大数据处理能力。
1 基于层次结构数据的偏回归系数计算方法
1.1 带加密数据库的层次结构数据
在大数据分析处理中,为方便数据的存储、读取、计算等操作,大部分数据都按照一定拓扑结构进行存储,如链式结构、网状结构、环形结构等,其中较为常用的一种数据管理结构为层次结构。
通过层次结构所组成的数据即为层次结构数据[21],层次结构数据具体关系见图1。在层次结构数据中,所有数据点组成一个层次化的垂直树形网络,每一上层数据集拥有下层分支的全部数据成员。在实际操作过程中,对一个共含有P层的层次结构数据集合,第P层的各数据集将全部数据传输到该节点对应的上层数据节点,然后对第P-1层的各数据集汇总,并传输到其对应的第P-2层数据节点上,每次往上一层汇总时,会对汇总层进行置空,以此类推,直到传输汇总到第1层数据节点。
通过层次结构化的垂直树形网络,数据被逐层传递汇总,在实际的计算分析中数据既可以在当前数据层进行处理,也可以在上层进行汇总处理。这样既可以保持统计规律不改变,又实现了并行处理,增加了数据的灵活性和可用性。基于此特点,层次结构数据在银行、金融、医疗卫生[22]等行业领域有着广泛的适用性。
同时在银行、金融、医疗卫生等行业领域中,数据集中往往包含着用户的隐私信息,因此多采用加密数据库进行存储、传输。在加密数据库中,每个数据库仅保留少量外部接口或对数据进行加密处理,两者加密方法都对基于全体数据的回归分析模型在构建上造成一定困难。为了对基于隐私数据的层次结构数据集进行回归分析,本文在传统回归分析的基础上,提出基于少量接口数据的回归数据计算方法,算法如下:
步骤1开始;
步骤2参数初始化p、P,令p=P;
步骤3由第p层接口数据求解部分偏回归系数Bp、层次结构矩阵Qp,令p=p-1;
步骤4由部分偏回归系数Bp、层次结构矩阵Qp,求解总体偏回归系数B;
步骤5判断p值,如果p>1转步骤2,如果p=1转步骤6;
步骤6结束。

图1 层次结构拓扑图Fig.1 Hierarchy topology
在该算法中,参数p为计数器,计算当前所在的层数,参数P是层次结构数据的总层数。算法中步骤2负责计算包含少量接口数据的下层部分偏回归系数,在充分保护数据隐私的前提下构建结构下层数据中小部分数据的MLR模型。步骤3负责利用下层部分偏回归系数以及数据传递时的层次结构矩阵计算上层总体偏回归系数。在步骤2,3的计算过程中,所有偏回归系数以及层次结构矩阵的计算仅需少量接口数据,因此本文算法能在构建层次结构数据MLR模型的同时,充分保障数据的私密性。步骤3,4的具体计算方法如下。
1.2 层次数据的回归建模
考虑一组已知的层次结构数据,采用MLR分析对其结构内数据进行建模计算,由层次结构的特点,本文考虑对其中任意上下两层数据子集进行分析。该数据子集中上层有一个部分,下层由K个部分组成,数据上下层之间满足层次结构,且下层之间数据相互独立。在此数据集的基础上本文考虑构建上层总体偏回归系数与下层部分偏回归系数之间的关系模型。
1.2.1 部分偏回归系数计算
以下将具体阐述下层部分偏回归系数的求解方法。为达到保护隐私的目的,本文方法只需少量接口数据便可进行下层每个部分偏回归系数的求解,其中接口数据包括原数据总和、平均值及交叉项乘积和。
在传统MLR分析中,利用最小二乘求解方法[23]求解偏回归系数仅需计算

式中N表示回归模型中自变量X的维数。
对式(1)中回归系数方程组系数矩阵L与L0=(L10,L20,…,LN0)T的计算方法通常如下

式中:N表示回归模型中自变量X的维数;n表示每一维自变量的样本数。
在式(2)算法中需要已知全体自变量X和应变量Y的原始数值才可以进行计算求解。但在一些特定场合中,原始数据是严格保密的,因此本文考虑通过原数据总和、平均值、交叉项乘积这类不涉及隐私信息、可用于传输的接口数据来构造部分偏回归系数方程组系数矩阵L和常数向量L0。
本文考虑对式(2)中的Lij进行展开计算,以此来设计新的方程组系数构造方法。展开后结果如下
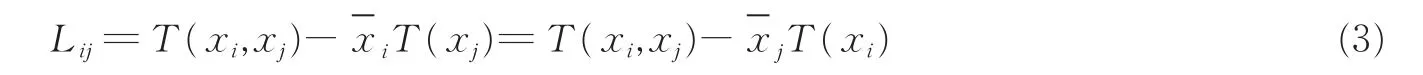
其次本文考虑对Lj0进行展开计算,可得到

式中:第i维自变量数据的平均值为;第i维自变量数据的总和为T(xi);与第j维自变量数据的交叉乘积和为T(xi,xj);应变量数据的平均值为-y;因变量与第i维自变量数据的交叉乘积和为T(xi,y)。
这样即可得到下层部分偏回归系数的两部分系数,非常数项偏回归系数

以及常数项偏回归系数

式中N为自变量维数;在式(5)中的矩阵A是由原数据总和、平均值、交叉项乘积所构造的系数逆矩阵,具体表达式为A=L-1。L0的具体表达式为L0=(L10,L20,…,LN0)T;在(6)式中为因变量的平均值,i为第i维自变量的平均值。
通过上述求解推导,本文旨在对于原有回归分析的求解方法做进一步展开合并计算,并通过原数据总和、平均值、交叉项乘积来构造式(1)方程组中的系数L,以此来求解部分偏回归系数B=[b1,b2,b3, …,bN]。同时在方程组求解过程中又引入系数逆矩阵A来替代原有的L,进一步化简的偏回归系数求解方法。
1.2.2 总体偏回归系数计算
本节将构建上层总体偏回归系数与下层部分偏回归系数之间的关系模型。
考虑MLR分析中最小二乘的矩阵求解方法

在本文模型对应的层次结构数据中,式(7)中的X、Y包含了K个数据部分,第k部分的数据为X(k)和Y(k)(k=1,2,…,K),由模型的线性可加性可知,式(7)中的XTX、XTY可表示为

由最小二乘法的矩阵表示形式可知,式(8)中的XTY可表示成

将式(8,9)代入式(7),可得第k部分结构数据的偏回归系数Bk与总体偏回归系数B之间的关系为

将X(k)TX(k)表示为层次结构矩阵Qk,进行展开计算后可得到

式中:X(k)为第k部分数据矩阵的扩展矩阵,即第1列数据全为1,第2列到最后一列为原始数据;第k部分数据的第i个分量的总和为T(X(k)i),平方和为T(X(k)i,X(k)i);与第j个分量的平方和为T(X(k)i,X(k)j)。
通过式(11)的计算方法,直接输入数据可得到Qk,结合计算Bk可以得到总体偏回归系数

式中:Bk为下层第k部分数据的偏回归系数;B为上层全体数据的总体偏回归系数。
基于式(12),可通过部分偏回归系数以及层次结构间的矩阵来计算任意p层与p-1层之间满足层次结构数据关系的偏回归系数。当层次结构数据由下往上按图1方式传输时,任意2层之间满足关系的数据就可构建上下层之间的偏回归系数模型,由此就可构建整个层次结构数据的偏回归系数关系模型。这种新的数据处理模式,对于具有层次结构的大数据处理具有重要意义。在不影响规律提取的前提下,一方面数据的分块处理能有效保护数据的隐私性;另一方面数据能分块处理可实现计算机的并行运算,提高大数据处理的能力。此外,通过理论推导可知本文的模型计算均为精确值。但在实际计算中,计算工具会导致截断误差的存在,不影响模型结果。
2 数据模型验证
在经济学研究中,多元性回归分析是一种常用的方法。本文参考韩琴等[24]在2017年提出的财政收入MLR模型,建立起2015年我国财政收入Y与人口数X1、最终消费支出X2、农业总产值X3、工业总产值X4、建筑业增加值X5、灾害直接经济损失X6之间的MLR方程,通过财政收入的MLR方程来验证本文所提方法模型的准确性。
同时为使数据呈现层次结构,本文将全国31个省市地区按照孙红玲等[25]提出的中国经济区的横向划分方法将全国31个省市地区划分为泛珠三角经济区、泛长三角经济区、大环渤海经济区,同时每个经济区分别包含12、10和9个省市地区,本文通过此经济区域划分来构建层次结构数据。具体结构如图2所示。
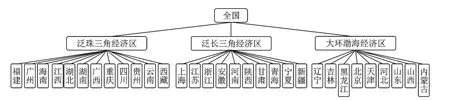
图2 基于横向划分的全国经济区域层次结构图Fig.2 The Horizontal Structure of National Economy Based on Horizontal Division
根据图2结构,参照回归模型中所需的自变量和因变量,从2016年统计年鉴[26]中可知表1列出的数据。
通过表1数据及相应的层次结构,进行回归系数模型的验证。在验证过程中,将本文模型所求结果与Matlab自带工具箱求解结果进行比较,以此作对比验证。
对于3个经济区的数据,采用少量接口数据求解每部分的偏回归系数,再通过文中基于接口数据求得的部分偏回归系数以及层次结构矩阵,求解总体偏回归系数。
在求解部分偏回归系数时,本文假设表1数据集中的3个经济区的具体数值是未知,仅知道3个经济区数据总和、平方和以及交叉项乘积和,具体数值如表2—4所示。

表12015年全国31个省市地区统计数据Tab.1 Statistics of 31 provinces and cities in the country in 2015
在表2—4中,总和与均值可以通过表1数据简单计算得出。而交叉项乘积和是需要进行计算的。通过表2—4中的数据,利用部分偏回归系数的求解方法可以将3个经济区每部分的偏回归系数计算出来。进而利用层次结构矩阵Qk构建的总体偏回归系数的求解方法去求解全国31个省市地区的总体偏回归系数,结果如表5所示。

表2 泛珠三角经济区接口数据表Tab.2 Interface data of the Pan-Pearl River Delta

表3 泛长三角经济区接口数据表Tab.3 Interface data of the Pan-Yangtze River Delta

表4 大环渤海经济区接口数据表Tab.4 Interface data of Circum-Bohai-Sea region
表5中的bi表示每一维自变量的偏回归系数。本文模型求解的全体偏回归系数与Matlab工具箱结果相比,两者结果之间的计算误差数量级为10-11到10-13之间,属于Matlab工具本身导致的截断误差,不影响模型及方法本身,因此两者方法本身并无差距,由此可说明本文的总体偏回归系数模型有效可靠。

表5 部分偏回归系数、全体偏回归系数以及Matlab工具箱计算结果Tab.5 Partial regression coefficients,total partial regression coefficients,and Matlab toolbox calculations
上述基于中国经济区的横向划分方法的31个省份财政收入的回归模型研究中,充分说明了本文提出的部分偏回归系数模型,以及基于层次结构矩阵的全体偏回归系数模型在实际应用中是可行、有效的。本文模型方法可在只提供原数据总和、平均值、交叉项乘积和等接口数据的前提下实现部分偏回归系数以及全体偏回归系数的求解,可适用于银行、医疗等领域在保护数据隐私前提下构建不同层次的回归分析模型。
3 结束语
本文针对大数据环境下海量的数据集以及数据处理的隐私保护问题,提出了基于层次结构矩阵来构建下层部分偏回归系数与上层总体偏回归系数之间关系的模型。理论推理表明模型可以利用原数据总和、平均值、交叉项乘积和这些带隐私保护功能的接口数据来求解部分偏回归系数。同时利用带隐私保护的接口数据求解层次结构矩阵,使层次结构矩阵也带有隐私保护功能,再通过部分偏回归系数以及层次结构矩阵求解总体偏回归系数,实现了全局模型的数据隐私保护。
同时以经济统计试验数据为例,验证了新模型的准确性。本文模型是对MLR模型及偏回归系数估计做出的有益的尝试,为大数据处理提供了更为快捷的方法,适用于不同行业的数据。同时,对于一些特殊行业的数据保密和隐私保护具有重要意义。
