一种基于关联频繁模式的振动数据流挖掘框架

2019-10-30张艳梅杨余旺

数据采集与处理 2019年5期

张艳梅陆伟杨余旺

（1.广东培正学院电子商务系，广州，510830；2.南京理工大学计算机科学与工程学院，南京，210094）

引言

轴承是大多数滚转机器的重要组件，约40%的滚转机器故障是由轴承故障造成，主要包括外圈、内圈和滚珠轴承故障[1]。目前，机器状态监测（Machine condition monitoring，MCM）技术主要是对磨损产物、电机电流、噪声、气温和振动信号等进行监测和分析，其中振动信号分析凭借其可靠性和灵敏性成为最有效的监测对象[2]。不同的故障类型会引起不同的振动频率成分，主要和轴承几何形状及运行速度有关系，其外圈、内圈和滚珠轴承故障所对应的振动频率成分函数表达式分别为[3]

式中：frm,dpitch,dball,n和φ分别为旋转频率、节圆直径、滚珠直径、滚珠数目和接触角。振动分析技术包括时域、频域和时频域分析。时域分析难以分离出不同振动源，而由于振动频率特性，频域分析成为主要分析手段，其中以能够将时频域振动信号转换为离散频率成分的快速傅立叶变换（Fast Fourier transform,FFT）为主[4]。因此，本文使用FFT对振动信号作频域分析。

信号频率域分析主要是从机器振动数据中提取故障信号特征，并使用机器学习技术从正常信号中识别出故障特征[5]。由于机器故障类型多和故障发生的偶然性使故障收集变得很难，通常使用模式分类技术解决此问题[6-9]，涉及小波技术、人工神经网络和支持向量机技术，但均存在故障识别精确度低的问题。目前已有研究将数据挖掘技术引入到故障诊断研究中，通过使用粗糙集、决策树融合等实现旋转机械、感应电机等的故障诊断决策[10-11]，相比传统模式分类技术具有较优的识别性能，结果显示数据挖掘技术在故障诊断领域具有很大的发展潜力。

频繁模式挖掘是数据挖掘领域的一种基本方法，但由于数据流环境具有数据量大、实时性、数据预知性差等特点，传统频繁模式挖掘算法难以适应。关联频繁模式挖掘算法由于具有更高的挖掘效率更适合于数据流环境，主要分为广度优先算法和深度优先算法两大类，广度优先算法有Apriori,Apriori-Hybrid等[12]，其在密集数据库环境下效率比较低。深度优先算法则以FP-growth[13],FP-Streams[14]为代表，其中FP-Streams算法使用频繁模式树存储过去时间窗口中的频繁模式项集信息，但当事务长度增加时算法效率会降低。由于现实应用中，人们更关心当前时间窗口内到达的数据流信息，因此一些学者将滑动窗口引入到数据挖掘之中。文献[15]研究了时间窗口长度固定和变化条件下的频繁模式挖掘算法，文献[16]针对滑动窗口数据挖掘算法，提出了一种数据结构闭合枚举树，用来存储动态选定项及其边界，降低了算法时间代价。因此，本文将关联频繁模式挖掘中的深度优先算法引入到对轴承振动数据流的数据挖掘中，再借鉴上述算法使用的滑动时间窗口思想分块求取频繁模式集。

本文提出了一种新的数据挖掘框架——关联频繁模式集挖掘框架（Associated frequency patterns mining framework，AFPMF），设计了一种基于滑动窗口的关联频繁模式树（Sliding window associated frequency pattern-tree,SWAFP-T）结构和SWAFP算法，挖掘振动数据流得到关联频繁模式集，识别故障频率，获得优于现有技术的故障识别性能。频繁模式挖掘技术受最小支持阈值约束，阈值大小影响频繁模式集数目。由于轴承振动信号从各角度分析会产生大量数据，需要寻找合适的筛选方法在振动数据中找到具有强相关性的频率特征模式。因此，本文将使用关联频繁模式从振动数据中寻找具有强相关性的频率特征模式，对通过已知故障数据得到的故障特征进行FFT分析，以提取故障的频域成分信息。最后，方案根据频繁模式集对轴承的缺陷状态实施监测，进而避免了轴承故障的发生。实验验证了方案有效性，结果表明本文所提出方案具有优越的检测效率和识别精确度。

1 数据预处理

数据挖掘框架AFPMF主要由数据预处理、关联频繁模式挖掘和故障频率识别构成。数据预处理过程主要处理从轴承数据寄存器中收集的振动数据。首先使用大小合适的矩形窗将振动数据划分为多个具有相同时间大小的子窗，长度为l的信号X被采样点数W的矩形窗划分为m个时间子窗，表达式为

其中，振动信号X的任意时间子窗i表示为

式中：i=1,2,3,…；w=1,2,3,…,W。受机器运行状态和环境影响，振动数据包含的故障特征信号会受不同程度水平噪声影响[17]。为分析不同噪声水平影响，时间子窗xi被高斯白噪声影响，表达式为

由于时间域信号的时变特性，将时间子窗信号xi转换到频域，其频域fi表达式为

其中当窗口尺寸为W时，fi包含W/2+1个频率，对fi归一化，即

其中频率具有连续幅值，关联模式挖掘要求频率使用二值表示即为激活态(1)或者非激活态(0)，使用阈值ε将-fi中的每个频率幅值转换为二值，其表达式为

式中：Ti包括在时间子窗i内所有幅值为1的频率信息。

2 挖掘关联频繁模式集

2.1 基础概念

设F={f1,f2,…,fn}为故障振动数据预处理后的频率集。假设时间被划分为等长时隙t={t1,t2,…,tq}，tj+1-tj=λ和j∈[1,q-1]，λ为时隙大小。集合P={f1,f2,…,fp}⊆F为频繁模式，振动数据流被定义为VDS=[e1,e2,…,en)，r∈[1,n]，er表示元组E(Ets,P)，其中P为元组所在相同时间Ets子窗内的频繁模式，设size(E)为E大小，表示频率数目。设每个窗口W内包含长度相等的非重叠序列的批，设有M序列和N批，批由M/N构成，故批大小为|MN|，设定窗以批为单位进行串序滑动。图1给出了振动数据流结构示意。

定义1窗口W中模式P支持集为SUPw(P)，如果某模式支持度大于支持度阈值MinSUP，有0≤MinSUP≤ |W|，则认其为一个频繁模式。再者，模式P的最大频率支持集为MaxfreqSUPw(P)=max(SUP(fj)|∀fj∈P)。

图1 振动数据流结构示意Fig.1 Structure diagram of vibration data flow

定义2设窗口W中模式P信任度为αw(P)，其表达式为

定义3如果αw(P)大于或等于窗口W中给定的最小信任度阈值MinallConf，则称其为关联频繁模式。

当给定振动数据流VDS，|W|，MinSUP和MinallConf等数据时，将关联频繁模式挖掘问题转换为|W|中大于某阈值条件下的模式集合寻找问题。

2.2 树构建过程

数据流VDS由无限长序列构成，批由非空集的序列构成。SWAFP-T树构建过程分为插入阶段和重构压缩阶段。

插入阶段，SWAFP-T树根据频率在数据流中出现的顺序依次安排频率顺序，并通过插入的方式排列VDS中先后出现的每个序列，并且维护一个存储所有频率支持度的频率头列表F-list，完成SWAFP-TA初始化。

初始化阶段SWAFP-TA结束后，开始重构压缩阶段，通过本阶段得到一个高度压缩的SWAFP-T，能够占用更小的内存空间和更快的挖掘处理速度。重构压缩处理过程使用文献[18]中提出的分支排序方法（Branch sorting method,BSM）。BSM使用合并排序排列前缀树上的每条路径，该方法首先移除未排序路径然后给其他路径排序，最后再将之前移除的路径重新插入排列。此外，使用文献[19]提出的压缩方法选择树上每条分支具有相同支持度的频率节点并将其合并为一个节点。SWAFP-T构造算法的具体描述过程如算法1所示。

算法1SWAFP-T构造算法

Function SWAFP-TACONSTRUCTION PROCESS

INPUT：VDS，MinSUP，MinallConf，目标窗，批，序列，初始排序表ISO；

OUTPUT：构成SWAFP-T树；

生成F-list;

生成前缀树为空的SWAFP-TA;

FOR每个批Bido

删除当前窗中孤立的批

FOR每个序列Ekdo

排列Ek的项；

更新F-list中频率支持度；

将Ek插入到SWAFP-TA；

END FOR

按频率降序从F-list中计算Ffd；

FOR SWAFP-TA的每个分支do

使用BSM算法重构压缩；

END FOR

ENDFOR

END

如图1所示，数据流被划分为4个批，每个批包含相同数目的序列，窗则由固定数目的非重叠批组成，图1中的每个窗有3个批。图2给出了窗1的SWAFP-T树构建过程。如图2(a)所示，SWAFP-T树初始化为空，并从“null”根节点开始构建。TS=1序列{f2f5f6f7f8}按顺序插入到树中，第一分支中f2为根节点之后的初始节点而f8为尾节点，fx:1表示频率fx的支持度值为1，如定义1所述。在插入第2条序列前，为维护F-list，将TS=2的频率排列顺序从{f1f2f4f7}变为{f2f5f6f7f8f1f4}，并将其插入到树中。图2(b)为插入批1后的树结构，图2(c)为插入批2的树结构，图2(d)为插入批3的树结构。重构压缩后的树结构如图2(f)所示。

图2 窗1 SWAFP-T树构建过程Fig.2 Construction process of SWAFP-T in window 1

当振动数据流移动到批4时，由于窗2不再包含批1，因此需要移除批1信息。当有些节点不包含批2和批3的信息时将被从树上去除。图3给出了窗2树构建过程，其中图3(a)删去了批1，图3(b)插入了批4，图3(c)是窗2最终构成的SWAFP-T树。

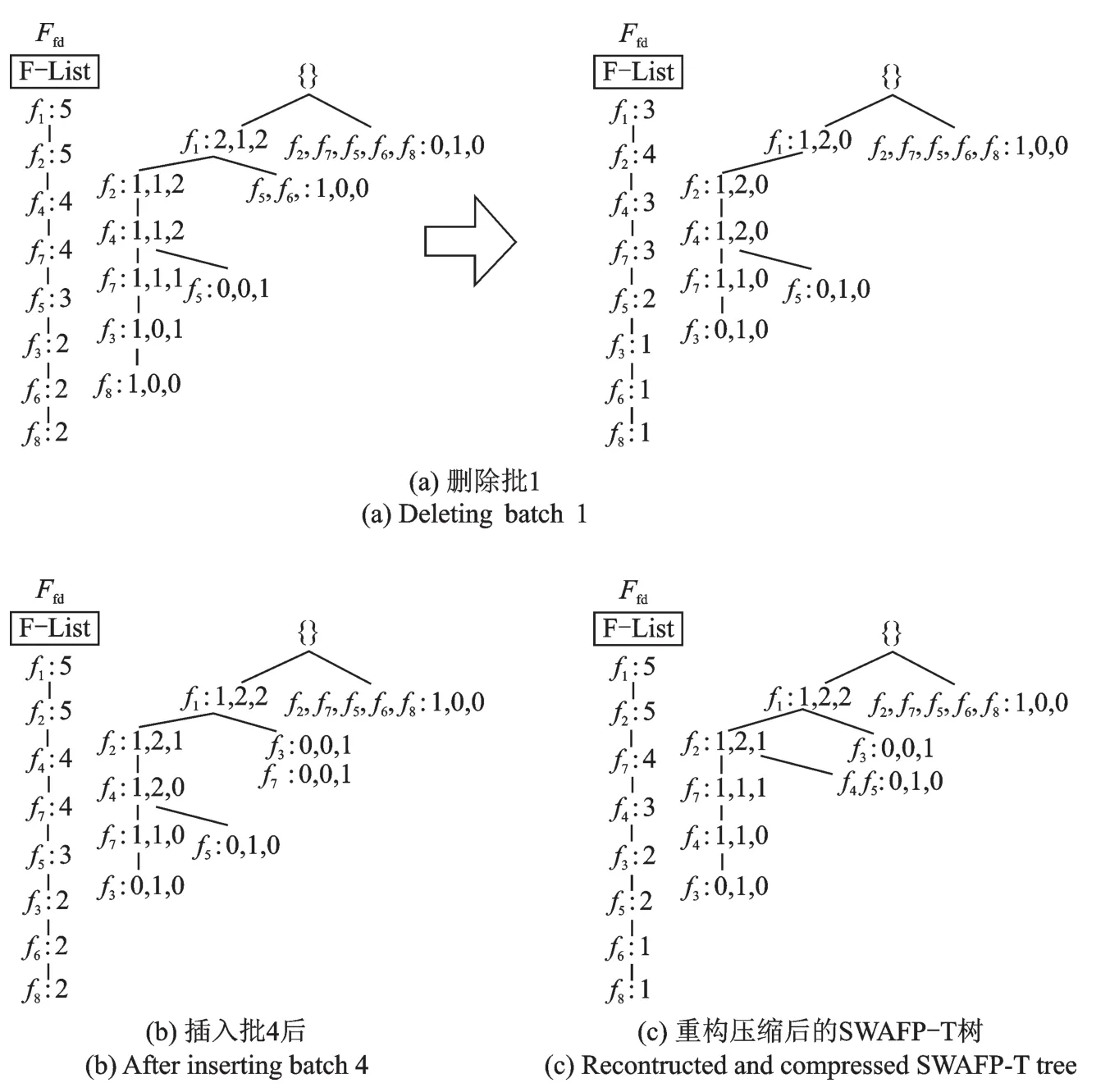
图3 窗2 SWAFP-T树构建过程Fig.3 Construction process of SWAFP-T in window 2

2.3 SWAFP树挖掘过程

从SWAFP-T树上挖掘关联频繁模式的基本操作包括：(1)记录长度为1的频繁频率点；(2)构建每个频率的条件模式基；(3)对每个条件模式基构建条件树。(4)从条件树生成关联模式集，这些过程总结起来得到挖掘算法流程如算法2所示。为了从图1给出的数据流挖掘出关联频繁模式，需要寻找窗1中的所有关联频繁模式集。假定

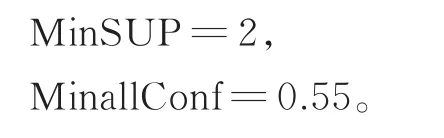
使用和文献[20,21]中类似的方法从SWAFP-T树上挖掘所有关联频繁模式，从Ffd底部频率开始建立条件模式基（Conditional pattern-bases,CPBs）和条件树（Conditionaltrees,CTs）。首先从图3(c)建立频率f5的条件模式基，这是因为最底部的f6和f8满足MinSUP阈值，因此从窗2的SWAFP-T树中的两个分支上提取出频率f5。由这些分支形成的路径分别为(f1f2f4f5∶1)和(f2f7f5∶1)。因此，考虑将f5作为后缀，其相关的生成条件模式基的两个前缀路径则分别是(f1f2f4∶1)和(f2f7∶1)，其条件模式基树见图4(a)。如图所示，条件树为空，频率f1,f4和f7不在条件树中，这是因为其支持度值为1小于阈值MinSUP，并且f1f5,f4f5和f5f7的所有信任度值均小于MinallConf。另一方面，尽管频率f2满足阈值MinSUP，但是其f2f5的信任度值小于MinallConf，所以频率f2也不在条件树中。因此，频率f5没有关联频繁模式。频率f3的条件模式基是(f1f2f7f4∶1)和(f1∶1)，如图4(b)所示。频率f4的条件模式基是(f1f2f7∶ 1)和(f1f2∶ 1)，其条件树只包含一个单路径(f1f2∶ 3)，如图 4(c)所示。f4的关联频繁模式集有(f1f4∶1)、(f2f4∶3)和(f1f2f4∶3)。表1给出了图1数据流在窗2下的关联频繁模式集的挖掘结果。

算法2SWAFP-T挖掘算法

Function Mining_process of SWAFP-T

Begin

Forfiin F-list do

从底部开始寻找长度为1的fi;

For eachfido

If位于fi底部的频点fj支持

＜MinSUP

删除fj;

以fi为后缀，将前缀路径作为CPBs；

End

For eachfjin CTs offido

Iffj支持度≥MinSUP&&fjfi

的信任度＞MinallConf

保留fj；

End;

所有保留元素fj构成CTs；

End for；

For all CTs offido

求出所有关联频繁模式集；

End for

End

图4 前缀和条件树构建过程Fig.4 Prefix and conditionaltree construction process

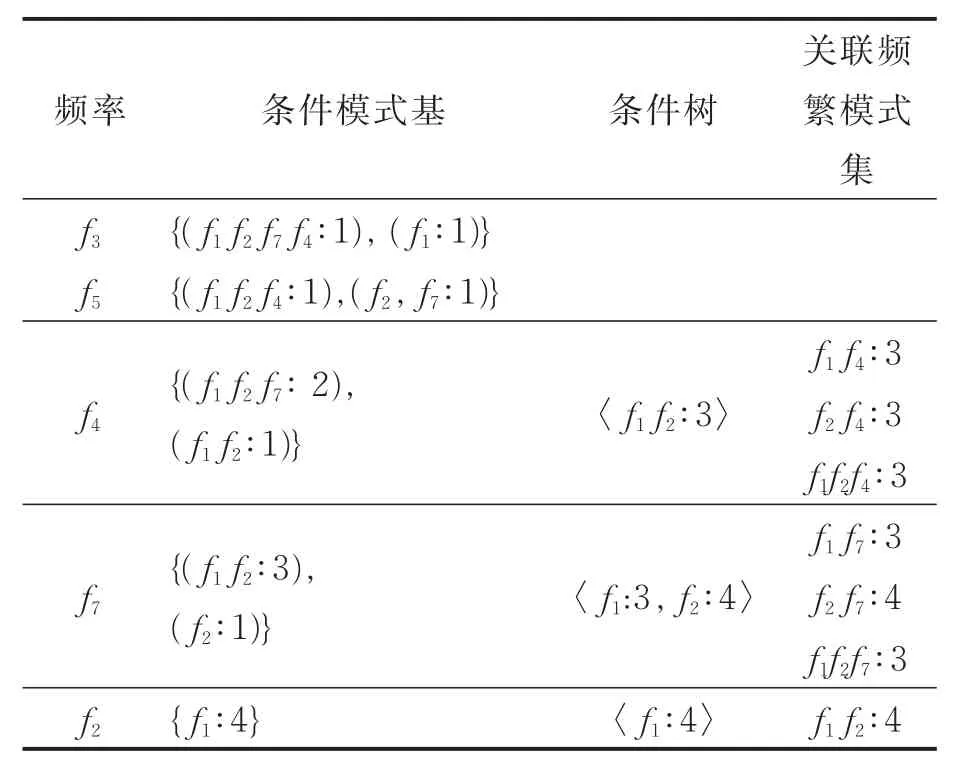
表1 窗2下的数据流关联频繁模式集挖掘结果Tab.1 Data stream association frequent pattern set mining results in window 2

3 故障状态监测

本节在AFPMF框架下利用SWAFP-T树进行故障概率识别，从而实现故障状态监测。首先计算故障特征频率，主要过程如下：检查频率信息表（表2），对比具有可疑振动频率信息的轴承ID，此具体频率信息由式(1—3)计算。若表中可疑振动频率出现在关联频繁模式集SWAFP-T树中，则认为该振动频率对应的器件有可能出现故障。以轴承1为例，若其轴速为350圈/min，则内圈故障频率为10.65×350=3727.5圈/min=62.125 Hz。

一旦SWAFP-T树中出现以上频率或者相应的谐波频率成分，则认为此轴承内圈有一定概率存在故障，进而启动相应的修复进程替换该潜在故障轴承。

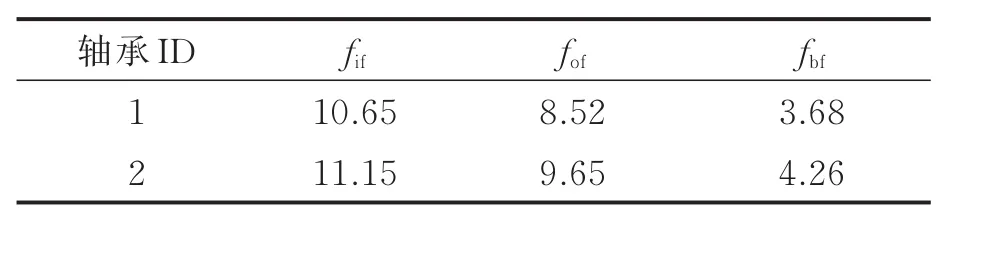
表2 轴承故障频率Tab.2 Bearing failure frequencyHz

4 实验结果分析

为识别故障频率，需要从故障轴承数据中挖掘所有的关联频繁模式集。实验分析了3种不同故障如轴承内圈、外圈和滚珠故障条件下的振动数据，数据收集使用16通道的数字式磁带录音机，采样速率为12000次/s。在AFPMF数据预处理过程中，将获得的每种故障振动数据通过Matlab软件FFT函数转换为频域数据。AFPMF中数据挖掘算法和故障状态监测均使用Matlab 2012b实现，软件运行硬件环境的CPU是2.8 GHz，内存为8 GB。

4.1 算法运行效率

首先，评估不同时间窗大小和不同批大小条件下AFPMF算法的运行效率。先将内圈数据集划分为12批，每批包含100条序列，窗口大小设为W=3B。在滑动窗口环境下，窗1包含了最开始的3个批次，分别为B1,B2和B3。同理，窗2包含的批分别是B2,B3和B4。再次重复实验时，数据划分为6批，每批包含200条序列，同样窗口大小为W=3B。图5(a)给出了不同阈值MinallConf时算法应用于内圈数据的执行时间对比，其中设置MinSUP为30%。图5(b)给出了批大小分别为150和300条序列并且窗口W=3B的外圈数据挖掘算法结果，实验中MinSUP固定设置为40%。由图5结果可知，算法运行时间在所有数据集下均会随着MinallConf的增加而下降。其次，图6给出了算法执行时间在MinallConf固定、MinSUP不同时的实验结果对比。从图6中可以看出，所有类型数据集下算法的运行时间均会随着MinSUP的增加而下降，这是因为候选模式集数目减小所致。

4.2 故障诊断识别性能

为识别故障频率，实验采用驱动端轴承，数据参数如表3所示，故障频率计算结果如表4所示。根据第3节中故障频率的计算公式，若表中可疑振动频率出现在关联频繁模式集SWAFP-T树中，则认为该振动频率对应的器件有可能出现故障。通过计算可知内圈、外圈和滚珠故障频率分别为 158，210和138 Hz。首先，检查在关联模式集中是否会出现故障频率和谐波成分。如果出现某类型故障频率，则说明该数据集对应的轴承部件有可能出现故障。实验结果显示，关联模式集中出现316 Hz频率，由于这是158 Hz的谐波频率，因此轴承内圈可能发生故障。本方案的优点在于只要有任何故障频率存在，不管阈值如何设置，SWAFP-T树均能够识别出故障频率。

图5 不同MinallConf时算法挖掘时间对比结果Fig.5 Experimental results of mining time at different Minallcof

图6 不同MinSUP时算法挖掘时间对比结果Fig.6 Experimental results of mining time at different MinSUP

4.3 故障诊断精度

为评估不同高斯白噪声干扰（0 dB到—10 dB）条件下算法对内圈、外圈和滚珠数据的故障诊断精度，定义故障诊断精度为加噪声后检测到的故障频率数目和加噪声前检测数目之比。

表3 轴承主要特征参数Tab.3 Main characteristic parameters of bearingscm

表4 故障频率Tab.4 Faillure frequengHz

以内圈数据为例，未加噪声时，主要参数有W=3B，B=100，MinallConf=55%，MinSUP=45%。实验得到了60个与316 Hz频率相关联的可疑故障频率，其中316 Hz是4.2节 158 Hz的故障谐波频率。加过噪声之后，在0和-2 dB时实验结果相同，而对于-4,-6,-8，-10 dB时分别得到59,57,56和55个关联频率数目。内圈、外圈和滚珠的实验结果如表5所示，其中外圈和滚珠的MinSUP和MinallConf分别为55%和65%,60%和70%。

本文将文献[6,8,9,11]中提到的4种算法作为对照算法，通过适当改进应用于振动数据流，结果如表6。据表6可知，AFPMF识别故障的精度显著优于现有技术。

表5 SWAFP-T算法精度Tab.5 Accuracy of SWAFP-T algorithm

5 结束语

本文提出了一种应用于轴承故障数据场景的数据挖掘框架AFPMF。在AFPMF框架中，首先使用FFT将振动数据流从时域转换为频域数据，再使用基于滑动窗口的挖掘算法SWAFP寻找到关于故障频率信息的关联频繁模式集，使用了具有高压缩、高效率可重构的SWAFP-T树用于关联频繁模式集的挖掘。最后，将关联频繁模式集直接应用于故障识别，实现故障状态监测。实验结果表明，本文所提方案有较快的算法执行效率，并且拥有比现有算法更优越的故障识别精度。