预紧力对滚柱直线导轨副刚度特性影响的研究

宋现春樊明贞王皓陈洪建荣伯松

(1.山东建筑大学 机电工程学院，山东 济南250101；2.山东博特精工股份有限公司，山东济宁272071)

0 引言

滚柱直线导轨副是数控机床的关键功能部件，其制造水平的高低在很大程度上影响了数控机床的发展。由于具有承载能力强、接触刚度高、摩擦阻力小、精度保持性好等优点，众多企业将其运用到工业生产中。

静刚度表示滚柱直线导轨副在承受外载荷时抵抗变形的能力。疏亚雅[1]利用Hertz接触理论分析了滚柱和滚道之间的受力关系，基于Palmgren公式建立了导轨副水平、垂直和绕主轴转动等3个方向的刚度模型，并对其进行有限元分析，探究了预紧力及滑块变形对静刚度的影响，结合试验数据分析得出，考虑群部变形所得静刚度与试验数据更接近；张巍等[2]运用齐次变换矩阵建立滚柱直线导轨副的刚度模型，分析了滚柱直线导轨副在不同预紧力和接触角下弹性变形量，找到了滚柱直线导轨副不同预紧力和接触角对其刚度特性的影响规律。

对导轨副动力学分析的关键在于对其结合面的动态特性研究。陈蓉等[3]基于ANSYS Workbench仿真软件对不同预紧力下滚柱直线导轨副进行仿真分析，得到各阶固有频率及振型，并结合模态试验，分析出不同预紧力对滚柱直线导轨副振动特性的影响规律。成建平等[4]利用弹簧单元代替结合面导轨与滑块的接触，采用Palmgren的经验公式，通过等效法得到弹簧单元的等效刚度，并验证了滚柱直线导轨副高刚度的特性。Shimizu[5]通过多滑块结构为基础，以变形协调关系为基础建立整体刚度模型，假设基础是以多滑块刚度一致进行，但与实际情况契合度不高。Ohta等[6]发现滚动直线导轨副的实测静刚度值远小于理论计算值，其原因是导轨副预紧之后滑块群部变形。还有学者对滚动直线导轨副的滚动体在承受偏载情况时，进行接触力学分析，建立了刚度与负载之间的函数关系[7-8]。

预紧力对直线导轨副的动静刚度有直接的影响研究，通常采用增大滚柱直径的方法增加预紧力，从而提高导轨副的刚度和承载性能。文章通过建立滚柱直线导轨副刚度模型，研究预紧力对滚柱直线导轨副弹性变形量及固有频率的影响，从而为研究其刚度特性提供依据。

1 滚柱直线导轨副的刚度特性研究方法

1.1 刚度特性的试验测量方法

以济宁博特精工股份有限公司的JSA-LZG45型滚柱直线导轨副为研究对象，该型号直线导轨副为四方向等载荷结构，相关参数见表1。

在结合面的基础参数中，刚度主要影响结构系统的固有频率和振动幅值，阻尼一般不影响系统固有频率，且在静力学分析中阻尼的存在并不影响分析结果。所以，在进行有限元建立模型时，采用等效法，将滑块与导轨结合面之间的滚动体等效为若干弹簧单元连接滑块和导轨，分别布置在4个滚道内滑块长度的1/4、1/2、3/4处[9-11]，如图1所示。

表1 JSA-LZG45型滚柱直线导轨副相关参数表

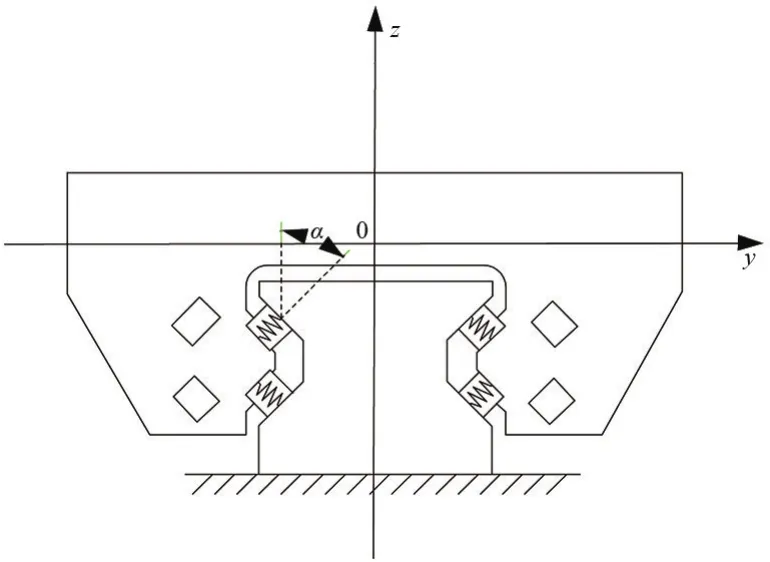
图1 阻尼弹簧单元的刚度模型图

静刚度试验采用滚动直线导轨副静刚度试验台装置进行试验研究，如图2所示。试验台是由机械主体、控制系统及测试系统组成的。机械主体主要包括床身、支撑立柱、被测导轨副、上横梁、加载头、滑块夹具和导轨夹具体等；控制系统主要包括驱动控制系统、交流伺服电机和液压比例加载系统等；测试系统主要包括称重传感器和位移传感器。

图2 滚动直线导轨副静刚度试验台结构图

试验台的主要功能是测量在垂直载荷下滚动直线导轨副的弹性变形量，在设计时应确定最大加载载荷(20%C)，可测导轨副的规格为35、45、55和65型滚柱直线导轨副。试验台采用液压加载，加载方式主要有:(1)匀速施加，到达最大值后保持最大载荷一段时间，然后匀速卸载；(2)阶梯式加载，按照最大加载力的百分比逐级加载，每阶段匀速加载达到指定值后稳压一段时间，直到加载力的最大设定值，然后以同样的方式卸载。试验采用阶梯式加载，可实现直线导轨副液压伺服的比例加载，加载力在0～100 kN连续可调，满足试验要求。

模态试验所采用的滚柱直线导轨副的结构与有限元模型一致。采用DHL050型号的力锤传感器对滑块进行激振，采用INV9822A型号的加速度传感器(适用测量频率比较高的机械结构)拾振。信号采集仪是东方振动和噪声技术研究所的INV3018C信号采集仪(8通道24位)，模态分析软件采用的DASP V10模态分析软件。现场装置如图3所示。

图3 模态试验测量装置图

锤击法是现场试验中应用较多的激励方式，优点在于体积小、易携带，试验的操作步骤简单，测试速度快，力锤产生的能量比较分散。由于LZG45型滚柱直线导轨副的结构较小、质量较轻，所以应尽量减小其附加质量及其影响。因此，在模态试验激励时采用多点激励单点输出的方式进行测量，传感器固定位置不变，力锤敲击所有的测点，并且在力锤敲击时应注意脉冲为单脉冲，避免试件与力锤的回击。

1.2 受垂直载荷时接触刚度计算

1.2.1 无预紧力时弹簧刚度计算

由于滚柱直线导轨副为四方向等载荷型结构，当滑块受到不同方向的载荷时，导轨副中总有2列滚柱承受外部载荷。每个滚柱在外部载荷的作用下与导轨、滑块分别构成一个接触副，所有接触副将产生弹性变形，从而使导轨副在力的方向上产生位移量[12-14]。采用Palmgren的经验公式计算得到每个滚柱的接触刚度，从而得到弹簧单元的等效刚度。

在垂直载荷F作用下，直线导轨副的i1、i2、i3、i4列滚柱中，只有i1、i2列滚柱承受载荷[15]，且每列滚柱承受的法向力为F′n，受力情况如图4所示。

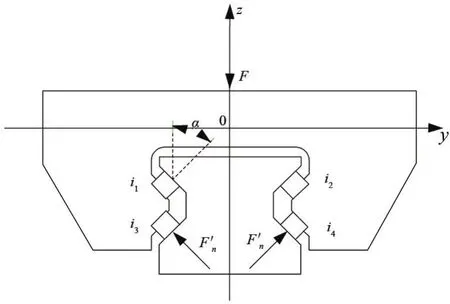
图4 受垂直载荷时滚柱直线导轨副受力图

每个滚柱受法向力F′n由式(1)表示为

式中:a为单列承载滚柱个数；α为接触角，°；F为垂直载荷，N。

由Palmgren的经验公式[16-17]，可求得每个接触副的法向变形量δn，由式(2)表示为

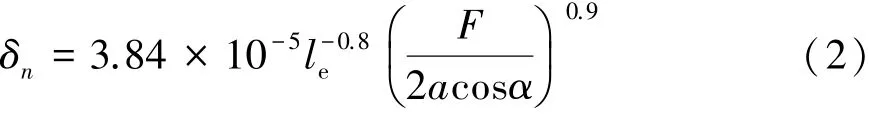
式中:le为滚柱与滚道的有效接触长度，mm。

由于每个滚柱同时与滑块和导轨构成接触副，且其在每个接触副的法向位移将导致导轨副在垂直方向上的位移，所以导轨副垂直方向的位移量δv由式(3)表示为

单个滚柱的接触刚度Kc由式(4)表示为

由于每个滚珠有2个接触副，所以每根模拟弹簧刚度Ks由式(5)表示为

1.2.2 有预紧力时弹簧刚度计算

为了增加滚柱直线导轨副的刚度及运动时的精度，采用增大滚柱直径的方法来施加预紧力。导轨副在垂直方向的弹性位移量δ0由式(6)表示为

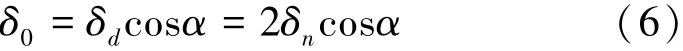
式中:δd为滚柱直径过盈量，mm。

i1、i2列滚柱产生的竖直方向作用力为F1，i3、i4列滚柱产生的竖直方向作用力为F2，由式(7)和(8)表示为

式中:δ为滚柱直线导轨副受垂直载荷时产生的弹性位移量，mm。

则求得垂直外载荷F由式(9)表示为

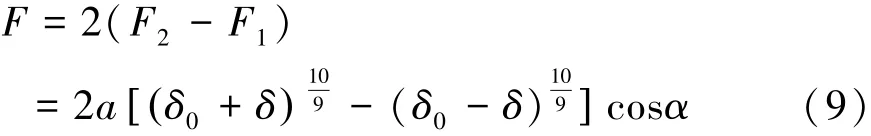
滚柱直线导轨副有预紧力时，求其静刚度要以i1、i2列滚柱刚刚失去预紧力时导轨副产生的垂直位移量来计算[18-19]，即i1、i2列滚柱与滑块脱离接触，此时δ=δ0，则F1=0，总的外载荷F由式(10)表示为

所以，当导轨副受预紧力时，每根模拟弹簧的刚度由式(11)表示为

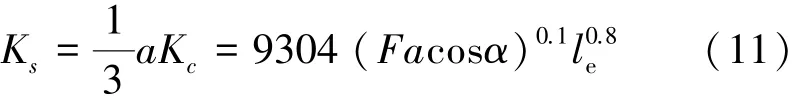
2 仿真结果分析

2.1 预紧力对垂直静刚度的影响

通过ANSYS Workbench仿真分析，得到不同预紧力对直线导轨垂直刚度的影响。分别取0.01C、0.05C和0.1C不同等级预紧力，在滑块上分别施加2、4、6、8、10、12、14 kN 的垂直载荷，导轨副的变形量见表2。

表2 不同预紧力下直线导轨副的变形量表

将垂直外载荷与导轨副变形量之间的关系转换为刚度曲线，如图5所示。无预紧力时，导轨副刚度为1 385.7 N/μm，轻预紧力时导轨副刚度为2 482.3 N/μm，中预紧力时导轨副刚度为2 713.2 N/μm，重预紧力时导轨副刚度为2 816.9 N/μm，因此，对滚柱直线导轨副施加预紧力可以显著提高导轨副的刚度。当施加轻预紧力时，刚度曲线斜率是无预紧力时曲线斜率的1.8倍，导轨副的刚度变化明显增大，继续增大预紧力时，刚度变化减小。同时，预紧力过大会加大导轨副的磨损，降低其的运行精度和工作寿命。因此，合理施加预紧力对导轨十分重要。

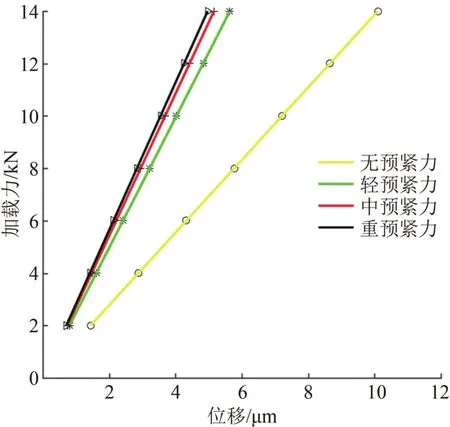
图5 预紧力对导轨副垂直刚度的影响图

2.2 预紧力对动刚度的影响

取0.01C、0.05C、0.1C等3种不同的预紧力，根据表1的相关参数，计算出对应的模拟弹簧刚度分别为170.04、177.66、180.51 kN/mm。将建立的三维模型转换成x＿t格式，导入到Workbench中进行仿真分析，得到不同预紧力下每阶模态的振动频率，结果见表3，不同振型模态结果如图6所示。可以看出，随着预紧力的增加，各级固有频率也随之增大，说明导轨副的固有频率受预紧力的影响。

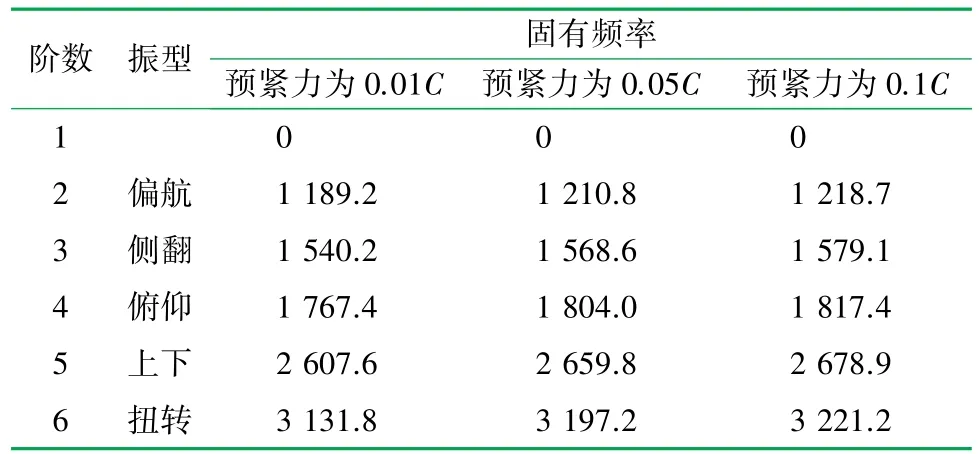
表3 不同预紧力下导轨副的固有频率表/Hz

为了更加直观的看出预紧力对导轨副固有频率的影响，绘制了折线图，如图7所示。当预紧力增大时，各阶固有频率也相应增大，这是因为直线导轨副的固有频率与刚度呈正相关，当导轨副预紧力增大时，其刚度也对应提高，进而各阶固有频率也相应增长，说明直线导轨副的固有频率与预紧力之间也呈正相关。施加较小的预紧力时，固有频率增长明显，当持续增大预紧力时，直线导轨副固有频率变化明显变小，所以适当增加预紧力可以提高导轨副动态特性。同时，预紧力过大也提高了接触面的摩擦力。因此合理选择预紧力大小直接影响直线导轨副的动态性能。

图6 滚柱直线导轨副的振型图

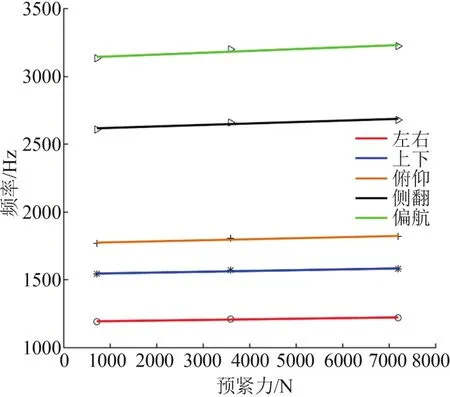
图7 预紧力对导轨副各阶固有频率的影响图

3 仿真与试验结果对比分析

3.1 加/卸载时静刚度结果

在进行静刚度试验时，为了消除滚柱直线导轨副与导轨夹具和滑块夹具之间的间隙，需要对滚柱直线导轨副施加预加载荷，然后以位移传感器调零时的数据为起点采集数据。随着加载力的不断增加，位移传感器实时采集滚柱直线导轨副的变形量，称重传感器实时记录加载力的变化量，然后进行垂直载荷的卸载，等到卸载完成后，得到相应的载荷增量和导轨副变形量的数据。加载、卸载时导轨副静刚度曲线如图8所示。

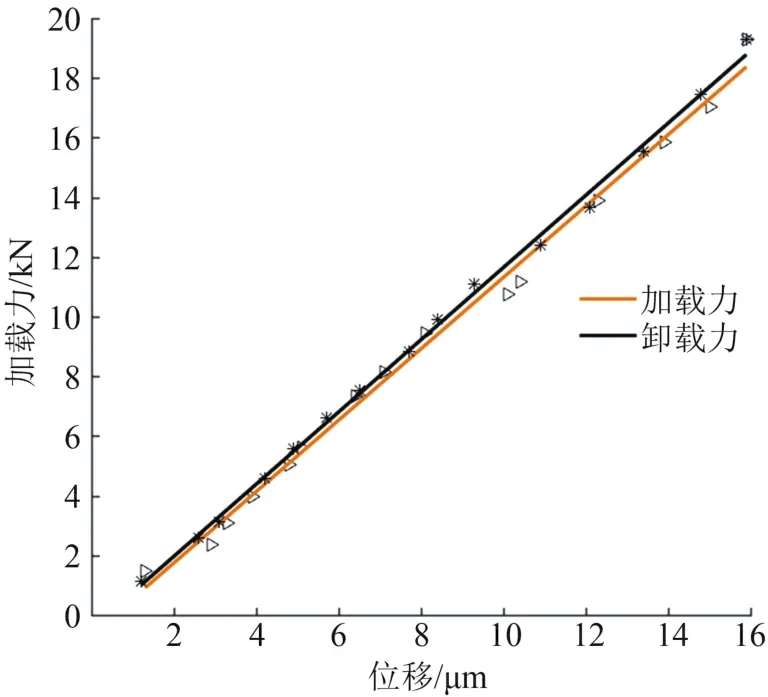
图8 加/卸载时静刚度曲线图

采用最小二乘法对载荷增量和相对变形量进行拟合，得到被测样件加载静刚度和卸载静刚度。可以看出，加载静刚度曲线和卸载静刚度曲线不完全重合，但非常接近，在允许的试验操作误差范围内，表明滚柱直线导轨副的性能满足试验要求。

将加/卸载状态下得到的刚度测量均值进行平均得到试验刚度，试验静刚度数据与Workbench仿真的数据进行比较，结果见表4。每次加载或者卸载时静刚度值浮动较小，其范围在5 N/μm内，加载与卸载相比静刚度值偏差较大，范围在15 N/μm内。与仿真相比，试验综合刚度误差为13.1%，考虑到试验台的测量精度，导轨副及夹具的安装精度，测量误差在允许的范围内。因此，静刚度试验台测量的数据是可靠的。

表4 滚柱直线导轨副静刚度试验数据表

3.2 不同预紧力导轨副静刚度对比分析

试验以JSA-LZG45型滚柱直线导轨副为研究对象，分别选择无预紧、轻预紧、中预紧、重预紧4种不同等级的预紧力导轨副进行静刚度试验测量，将其与仿真数据进行对比。预紧力的等级通过更换滚柱的型号来调节，滑块、导轨等采用同一样件。为了提高数据准确性，其他变量全部统一。

根据位移传感器在各数据采集点的测量值，计算得到相对于预加载时的载荷及变形量。采用最小二乘法对载荷增量和相对变形量数据进行拟合处理，通过数据拟合得到不同预紧力时导轨副静刚度的对比曲线图，如图9所示。当施加轻预紧力时，导轨副的刚度变化明显，静刚度增长量为835.58 N/μm，继续增大预紧力时，导轨副的刚度变化显著减小；中预紧时静刚度增长量为91.49 N/μm；重预紧时静刚度增长量仅为34.20 N/μm。试验表明:施加较小的预紧力就可以获得较大的导轨副静刚度，随着预紧等级的增大，静刚度的增长量逐渐变小。

图9 导轨副静刚度试验对比曲线图

将滚珠直线导轨副静刚度仿真数据和试验数据进行对比，结果如图10所示。静刚度仿真值和试验值均随着预紧力的增大而增大，但是导轨副静刚度试验值均低于静刚度仿真值，轻预紧时，二者相差441.82 N/μm；中预紧时，二者相差 581.23 N/μm。随着预紧等级的增加，相同预紧等级时仿真与试验之间的偏差量逐渐变大。

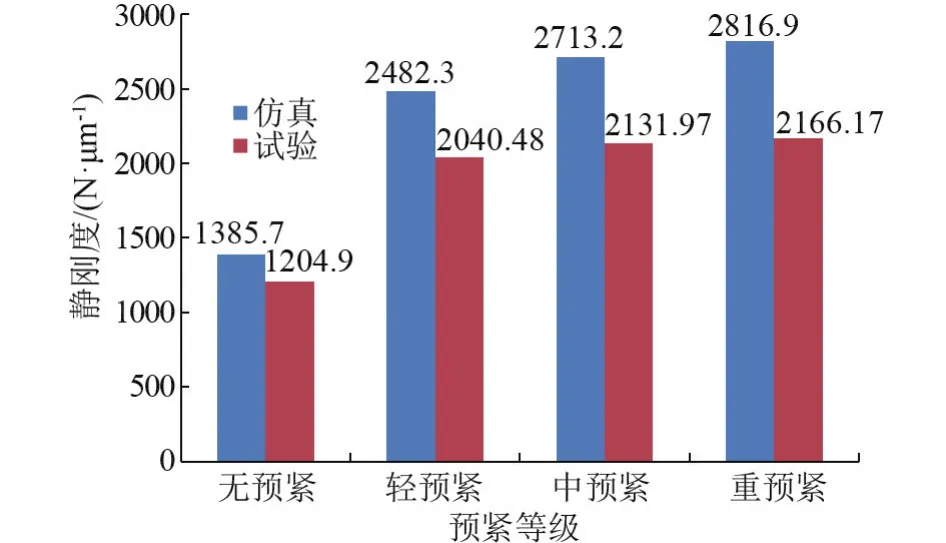
图10 滚柱直线导轨副静刚度仿真与试验对比图

3.3 滚柱直线导轨副模态试验研究

模态试验主要是对导轨副进行结构动力学分析，获得其固有频率、振型、模态阻尼和模态刚度等模态参数。通过加速度传感器和力锤传感器获得导轨副的振动信号，振动信号经过数据采集仪和模态分析软件对结构的试验数据进行处理和分析，获得导轨副固有频率、振型等关键参数。

滚柱直线导轨副的高阶模态频率都很高，力锤不能将高阶模态激发出来，也超出了所使用的传感器的识别范围。所得到的振型与仿真结果基本一致，基本确定试验操作的准确性。试验所采用的加速度传感器是单轴加速度传感器，只能拾取单维度的振动位移，且在进行激励时只敲击了滑块上表面的测点，忽略了滑块侧面的测点。所以在ADSP V10软件中，用模态分析模块进行数据分析，只提取了滚珠直线导轨副滑块的低阶模态。

试验采用轻预紧、中预紧和重预紧3种预紧等级的导轨副进行模态试验，在相同试验条件下进行测试，结果见表5。可以看出，不同预紧力等级下导轨副试验模态值和仿真模态值基本吻合。随着导轨副预紧力增大，其固有频率也随之增大。

表5 不同预紧力等级导轨副固有频率数据表/Hz

4 结论

文章建立了滚柱直线导轨副的阻尼弹簧单元的刚度模型，基于ANSYS workbench有限元仿真分析了预紧力对滚柱直线导轨副刚度特性的影响规律，并结合试验对仿真结果进行了对比分析。主要结论如下:

(1)施加较小的预紧力就可以获得较大的导轨副静刚度，但随着预紧等级的增大，静刚度的增长量逐渐变小。对滚柱直线导轨副合理施加预紧力，可以显著提高导轨副的静刚度，提高滚柱直线导轨副的承载能力。

(2)当滚柱直线导轨副的预紧力增大时，各阶固有频率也相应增大，持续增大预紧力时，滚柱直线导轨副的固有频率变化明显变小。合理选择预紧力大小有助于提高滚动直线导轨副的动态性能。