体表形态凸角对腰围间隙量的影响

应 欣， 程碧莲， 刘 正,2,3， 邹奉元,2,3

(1. 浙江理工大学 服装学院， 浙江 杭州 310018； 2. 丝绸文化传承与产品设计数字化技术文化和旅游部重点实验室, 浙江 杭州 310018； 3. 浙江省服装工程技术研究中心， 浙江 杭州 310018)

间隙量是指着装状态下服装与人体表面的空隙部分，是影响服装合体性、舒适性和三维虚拟试衣质量的关键因素[1],服装合体性是人们选购服装最关注的问题[2]。服装个性化版型设计的本质是根据款式特点将人体形态信息和松量组合成为合体的着装空间形态，因此，间隙量分布对版型设计与修改起着关键的指导作用。

目前，国内外学者针对人体与服装之间的空间关系研究主要集中在面料、放松量与着装间隙量的关联。徐继红等[3-4]从服装合体性角度研究了服装松量、面料性能与服装廓体松量的配伍关系；张爱萍等[5]采用三维扫描仪采集间隙量数据，建立了特定角度处的距离松量与平均距离松量的相关关系和回归方程；Agne等[6]和于淼等[7]通过研究织物力学性能与服装空间形态、体积的关系，改进了三维虚拟试衣软件的适体性，提出织物性能影响衣下空间体积的回归方程。而在现有应用的服装CAD软件中，人体着装模型主要根据织物物理仿真的弹簧质点模型和曲面碰撞检测方法进行构建，其方法对于宽松服装而言建模效果较差，主要原因是缺乏差异体型和不同面料下的间隙量数据。

服装依附于体表进而形成千姿百态的造型，从空间构成要素分析，人体形态特征对间隙量构造与分布起着基础且关键的作用。上述学者主要是以尺寸松量和面料物理性能对衣下间隙量分布影响为研究对象，而对于人体形态对着装衣下间隙量分布的影响研究鲜有见到。

本论文以人体的体表形态凸角对腰部截面间隙量的影响为研究对象，采用补正人台的方法构造递进的体表形态凸角，利用三维扫描仪采集净体与着装2种状态下的点云数据，通过Geomagic软件重建着装模型后，计算体表点法线方向的距离来确定着装腰部间隙量值，分析不同松量下体表形态的胸突角和背入角与间隙量分布的相关性，并建立腰截面间隙量与胸突角、背入角及腰围松量之间的回归公式。研究结论对不同体型其号型服装的合体程度，基于局部特征的服装个性化样板生成，以及虚拟试衣软件中间隙量的设置具有参考意义。

1 实验部分

1.1 体表形态凸角

女子体型分类中人体的躯干表面共形成7个角度：肩斜角、体侧角、胸突角、背入角、背侧角、臀突角、腹突角[8]。由于本文研究胸腰形态对腰部间隙量的影响，因此选取胸突角和背入角这2个能体现胸腰形态特征的体表角度作为研究对象，如图1所示。

注：α为胸突角； β为 背入角。

1.2 人台改造

静止状态下同一形态人台和真人的着装间隙量分布规律基本无差异，采用人台作为着装载体能够固定着装姿势。为避免呼吸、站姿等因素对体表角度和间隙量的影响，本文采用在人台上穿着不同厚度胸衣对人台进行补正，并采集补正后人台的着装间隙量值。所用人台为国家标准人台(如图2所示)高度为160 cm，胸围为84 cm，腰围为66 cm，臀围为90 cm。在人台初始的胸突角和背入角基础上，构造了穿着6种不同厚度胸垫人台的胸突角(如图3所示)。通过测量角度，将其编号为X1～X7并作为胸突角的参数规格。同理，在原有背入角的基础上，以2°为1个档差制作3个具有差异的背入角人台并将其编号为Y1～Y3(分别为13.96°，15.96°，17.96°)。具体样本规格参数见表1。

图2 实验人台Fig.2 Experiment mannequin

图3 胸突角测量

表1 胸突角规格参数表

1.3 样衣制作

本文选取浅色的棉布作为实验用样衣材料，设计并制作8件不同放松量的无领无袖样衣，编号为1#～8#。在贴体(胸围放松量0～4 cm)、合体(胸围放松量6～12 cm)和宽松(胸围放松量16～24 cm)的3类服装规格中，分别以胸围1、2和3 cm为档差制作1件贴体、4件合体和3件宽松规格的样衣。所有样衣的臀围与胸围相同，贴体和合体样衣腰围比胸围小16 cm,宽松样衣腰围比胸围14 cm[9]。具体样衣规格见表2。

表2 样衣规格表

1.4 实验过程

实验设备采用[TC]2三维人体扫描仪。首先，确定人台位置与姿势，得到人台净体的三维数据，保持人台位置和姿势不变，分别穿着1#～8#样衣进行扫描，得到1#～8#样衣穿着状态下的三维点云数据。然后，对穿着胸垫的补正人台进行扫描，得到补正人台数据，保持补正人台位置和姿势不变，依次套入1#～8#样衣进行扫描并得到三维点云数据。以同样的方法，获得背入角补正后的净体人台和穿着8件样衣的三维点云数据。为避免实验操作的人为误差，每件样衣在每个档差规格下扫描3次，无异常情况下取均值数据作为实验结果。

1.5 腰截面间隙量获取

1.5.1 腰截面坐标数据读取

将三维人体扫描仪得到的点云数据导入到Geomajic 软件，删除人体躯干以外的其他的部位，如图4所示。在净体人台模型中导入着装模型，将 2个模型以位置坐标为基准进行注册对齐，具体见图5。在Geomajic软件中采用构建平面[10]的方式选取研究所需的腰围截面，然后采用等距离采样法采集腰围截面上60个坐标点的坐标，采用多项式分段拟合人体和服装的腰围截面曲线。

图4 着装前后人台衣身

1.5.2 腰截面间隙量数学模型

着装间隙量狭义上是指同一水平面上人体到服装的最短距离[11]，本文采用人体腰截面表面点到服装的法线距离来定义腰截面处着装间隙量。

设人体腰截面上点A(a1,b1)处曲线方程为f(x),则该点的法线方程为

(1)

该法线与服装上的2个相邻点D1、D2的连线交点为B1，与服装的交点为B，如图5所示。

图5 人体法线与服装交点

将法线方程(1)改写为

A1x+B1y+C1=0

(2)

直线D1D2的方程为

A2x+B2y+C2=0

(3)

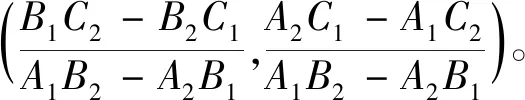
设通过点D1、D2的服装曲线函数为

(4)

将法线方程(1)改写为

N(x)=ex+g

(5)

则法线与服装的交点B为q(x)=g(x)-N(x)的一个零点。

采用牛顿迭代公式，利用B1点作为初始值对q(x)采用式(5)进行迭代：

(6)

式中ai是点B1的横坐标，一般通过牛顿迭代公式迭代几次就可以得到B点的横坐标a2,将a2代入式(5)中即可求出B点的纵坐标b2。

则腰截面处人体法线到服装的距离(见图6)为

(7)

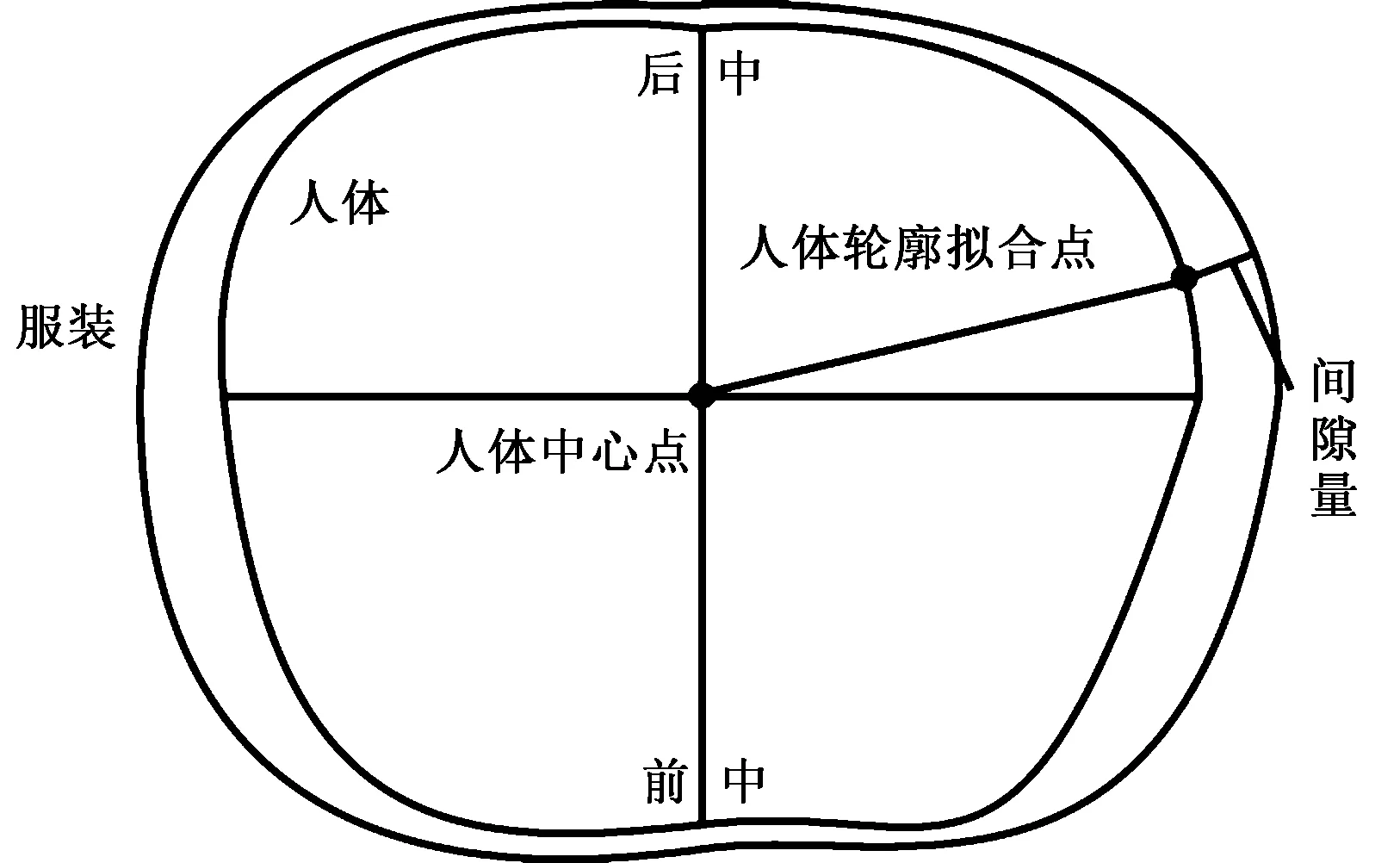
图6 腰截面间隙量示意图

2 间隙量与体表形态凸角的关系

为更清晰地表示体表形态凸角与间隙量分布的关系，以人体截面中心为坐标原点，每隔30°角作1条射线对腰围截面进行区域分割，如图7所示，计算各角度区域的间隙量的分布特征。

图7 不同胸突角腰围截面图

2.1 腰截面间隙量与胸突角的关联分析

图8示出不同背入角的腰围截面图。可以看出腰围截面间隙量的分布基本是以纵坐标为轴对称变化。为便于分析和表述，本文选取右边0°～180°区域为对象，研究腰截面间隙量的分布规律。

图8 不同背入角的腰围截面图

2.1.1 胸突角单因素分析

图9示出不同胸突角的腰围面间隙量分布，发现腰部间隙量整体呈现非均匀分布。胸突角为X1时，间隙量在人体的侧面60°～120°区域分布较大，且在60°～90°区域的分布大于90°～120°区域，即人体后腰的间隙量大于前腰的间隙量。这是因为这些区域位于腰围的侧面部分，由于后面有肩胛骨的支撑，前面有BP点的支撑，使得该区域相对较平坦，间隙量集中在该部分；随着胸突角度的增加，间隙量的分布从0°～60°区域逐渐转移至60°～180°区域，其中大部分转移至侧面60°～120°区域；由于手臂的因素，在90°区域间隙量并无明显变化，而在120°区域，间隙量大小与胸突角呈显著性正相关，相关系数为0.941。

2.1.2 放松量与胸突角联合分析

在人体侧面即60°～120°区域，间隙量数值与腰围放松量档差呈现正相关变化。而在0°～60°区域与120°～180°区域，放松量较小的样衣即1#～4#，后腰的间隙量小于前腰，放松量较大的样衣即5#～8#，后腰间隙量大于前腰。

胸突角度的变化对不同放松量下的服装腰截面间隙量分布有着显著的影响。对于2#～5#样衣，随着胸突角的增加，间隙量从30°～60°区域向60°～180°区域转移，且这种趋势在样衣5#中最为明显，其中120°区域间隙量与胸突角呈高度正相关变化,相关系数为0.941。这是由于人体左右两侧BP点的支撑使得前中部位形成较为稳定的空间，当胸突角度从X1～X7增加时，前中部分即120°～180°区域的间隙量值逐渐变大；对于1#、6#～8#样衣，胸突角与间隙量之间呈弱相关变化，虽然随着胸突角的增加，间隙量的分布也从0°～60°区域向60°～180°区域转移，但其变化量并不明显。这是因为贴体型服装在腰部一般紧贴人体，胸突角的变化并不会对间隙量分布产生大的影响，而松量过大的服装，BP点对服装的支撑作用小于重力对服装的作用，改变胸突角的大小无法对间隙量分布产生影响。

2.2 腰截面间隙量与背入角的关联分析

2.2.1 背入角单因素分析

随着背入角的增大，0°～90°区域的间隙量增大，其中0°～60°区域间隙量与背入角呈高度正相关变化，相关系数均高于0.9。在0°～30°区域相关显著性均为0.001；90°～180°区域的间隙量变小，其中120°～180°区域间隙量与背入角呈中度负相关变化，相关系数都在-0.8以上；由于手臂的原因，90°区域间隙量与背入角变化无关联。

2.2.2 放松量与背入角联合分析

背入角大小对不同松量服装有着差异化的影响。对于1#样衣，背入角的变化对间隙量分布的影响较小，在0°～30°区域间隙量与背入角呈低度相关变化，在60°～180°区域间隙量与背入角无相关关系，这是因为贴体型服装腰部间隙量的大小受肩胛支撑点的影响很小；对于2#～8#样衣，随着背入角的增大，间隙量的分布发生变化，在0°～60°区域的显著性均小于0.01其中后中部位0°～30°区域的相关显著性均达到了0.001，相关系数在0.9以上。这可以解释为人体左右两侧肩胛点对具有一定松量的服装有支撑作用，背入角越大肩胛骨就越突出，从而导致后中部位间隙量发生明显变化；120°～180°区域的相关显著性均小于0.05，进一步说明背入角对具有一定松量服装的腰部间隙量分布有显著影响。

3 回归分析

从上述的2.1、2.2节分析得知，在2#～5#样衣中腰截面间隙量与胸突角、背入角及腰围放松量呈现了高相关性，因此，本文针对0°、30°、60°、120°、150°和180°区域的腰截面间隙量，以胸突角、背入角及腰围松量为变量，进行多元线性回归分析[12]。回归方程如表3所示，定义y为特定角度处的间隙量，x为腰围松量，α为胸突角，β为背入角。

表3 不同角度处间隙量的回归方程

在各区域的回归分析中，30°区域和120°区域的间隙量与胸突角、背入角及腰围松量的相关性系数最高，回归方程的拟合优度也最好，回归方程的R2值都达到0.95以上。60°区域和150°区域的相关系数稍低，回归方程的拟合优度稍差，回归方程的R2值分别为0.776和0.879。

4 结 论

本文将体表形态凸角作为研究腰部着装间隙量分布规律对象，通过[TC]2三维扫描仪的测量实验，获得系列档差胸突角、背入角的补正人台及其穿着不同松量样衣的点云数据，计算得到腰截面各区域间隙量的数值，得到体表凸角与腰部间隙量分布的关联。

实验结果显示：1#样衣腰截面间隙量不受胸突角和背入角的影响，2#～5#样衣同时受胸突角和背入角的影响，6#～8#样衣受背入角影响，不受胸突角影响；其中胸突角对腰截面120°区域影响最大，背入角对0°～30°区域影响最大；胸突角和背入角都对侧缝区域的间隙量无影响；30°区域和120°区域间隙量与胸突角、背入角及腰围松量回归方程拟合优度较好，回归方程的R2值为0.968和0.979。这些结论对于下一步研究如何将间隙量分布转化为样板修改规则，以及提高虚拟试衣的仿真程度有着很好的参考和意义。