基于传统理念的风景建筑体量参数化控制研究

陈 烨

马文倩

1 风景建筑体量控制研究

1.1 传统风景建筑体量控制理念

乐山乐水者传承山水文化之精髓，在山水之间营造建筑，是山水文化的必然追求。正如郭熙所言：“君子之所以渴慕林泉者，正谓此佳处故也”“山之人物以标道路，山之楼观以标胜概”[1]。也因此，山水之间的风景建筑被郑绩称为“山水之眉目”[2]。作为“眉目”，便有了点睛抑或点景的含义，在尺度控制上也就有了一定的章法和约束。

传统风景建筑的尺度控制多以感性描述为主。在自然山水背景下，秦汉宫苑是将人工建筑散布于自然山水之中，追求弥山跨谷的气势；在写意山水理念中，强调“终南移入户庭间”(白居易《累土山》)。二者尺度跨度巨大，却又在天人一体的自然山水观中完美融合。

自然山水中的建筑营造追求增补互益的效果，如清代施闰章所言：“山水之有亭楼，犹人之高冠长佩也，在补其不足，不得掩其有余”[3]；在小尺度环境中，则运用考量规模限度的方法，如吴亮在《止园记》中提出：“园亩五十而赢，水得十之四，土石三之，庐舍二之，竹树一之”[4]，与王世贞描述小祗园“土石得十之四，水三之，室庐二之，竹树一之”[5]颇为一致，其余文献中所述大抵如是。

传统的体量控制方法有较大的或然性，今天我们研究山水之间的建筑营造，是在自然山水的真实尺度下展开的研究。陈从周先生曾提出风景建筑尺度控制的方向，如其在《说园》中所认为的那样：“风景区之建筑宜隐不宜显，宜散不宜聚，宜低不宜高，宜麓不宜顶。[6]”这句话既包含了选址概要，也包含了尺度控制的态度，只是具体量化的控制方法还需要进一步探索。

1.2 基于Civil 3D的体量研究思路

当前针对风景建筑对景观环境影响的研究文献较少，其中针对风景建筑尺度的研究，大多缺少明晰的方法体系。如波兰克拉科夫工业大学的Ozimek等从景观质量的角度，通过数字化计算结合图形分析的办法，研究了在景观环境中观赏距离、建筑类型和建筑规模对景观质量的影响[7]，是对景观质量定性定量的分析；其他在研究方向上接近的有胡一可等的《基于互动式眺望模型的风景区边缘区建筑高度控制研究》[8]、徐磊青等的《山景城市天际线的偏好与景观知觉：建筑高度与视廊数量的影响》[9]，以及美国景观建筑协会理事会(FASLA)的风景质量顾问Palmer等从人的视野、视域、视敏度和像素取样捕捉视觉信号等技术角度对风景的评估等[10]。

在山水之间营造建筑，需要针对特定的山水形态做出充分评估。如选址山麓、山腰，需要细究山形，山形板则破，山形虚则补，或增、或补、或破、或立，皆有其妙处。传统描述山体的形与势，在现代专业语汇中就涉及高程、高度、坡度、坡向、空间和比例等一系列环境要素。当代风景建筑体量的控制研究，应当在三维空间中解析上述诸环境要素，找到量化与计算的方法。

Autodesk Civil 3D是专业处理地形要素的软件，在基于地形信息建立的三维动态工程模型中，所有曲面、断面等均以动态方式链接，可用于快速完成道路工程、场地、雨水/污水排放系统以及场地规划设计等。借助该软件，可以对场地模型进行便捷的曲面建构和修改，并可对曲面高程、坡度、坡向和汇水等相关数据进行多方面的可视化和交互性分析。

风景园林建筑体量是三维空间中的体量，可拆解为水平方向的建筑占地面积与垂直方向的建筑高度2个关键指标。以选址山地为例，可通过采集场地的竖向信息，建立山地坡体形状的数字地形(曲面)模型，利用Civil 3D提取等高线，进行坡度分析以及视线影响区分析，根据风景建筑与地形竖向要素之间的相关因素，以及游人对空间尺度的视觉感知特性，解析建筑边界范围、建筑与山体轮廓的参数因子，从而针对山地环境中的建筑设计构建参数控制模型，建立基于建筑密度的面积控制算法。进而充分利用数字地形模型数据处理与分析的优势，通过生成曲面纵断面进行数据分析，并依据坡形比值研究对建筑高度的限制条件。

在运行计算的过程中，结合前期对江南传统优秀风景建筑的数据分析成果，运用风景环境中建筑密度的指标区间、基于坡体形状的指标参数区间，为山地环境中建筑体量的计算提供参考依据。

2 基于Civil 3D的参数化体量控制算法

2.1 控制建筑占地面积的算法

宋代是风景建筑的高速发展时期，王希孟的《千里江山图》中呈现了多样化的建筑形制。细观山中建筑，体量组合多变、疏朗有致。宋代的文人园林也以疏朗为主，有“三分水、两分竹、一分屋”的说法，建筑数量得到控制，不像明清时期通过游廊及建筑划分空间而呈现出的高建筑密度。至清代，龚贤指出：“凡安寺观大小，亦宜视山之深浅、林之厚薄、设桥亦然，小桥、板桥止可设于平滩沙水之际；深山大泽，须用石桥。楼台宜耸出在松楸林木之外，然亦须衬贴。大石桥边必有古寺。[11]”这一观点充分体现了因山构室、因穴成屋的重要思想。建筑因特定山体空间形态而选址，视特定的可建设用地而控制规模，正是对多变的山体形态的呼应。

本研究以平整的土地特性提取空间范围，通过可建设用地的面积倒推建筑占地面积。

1)地段可建设面积的获取。

(1)等高线范围的划定：首先选择建筑基址所在空间，将可建设坡度阈值定为0～25%，形成满足坡度要求范围的边缘等高线，构建基于坡度选择的建筑选址初步范围(图1)。

(2)可视域范围的确定：进一步通过Civil 3D的视线影响计算模块，根据地段内道路及可视方位进行视线影响区分析。基于视线双向可逆的原理，设定以坡形限高比方法计算出的建筑高度作为计算基准高度，通过计算得出可视域范围，在该视域范围内观与被观均可满足(图2)。

图1 等高线提取

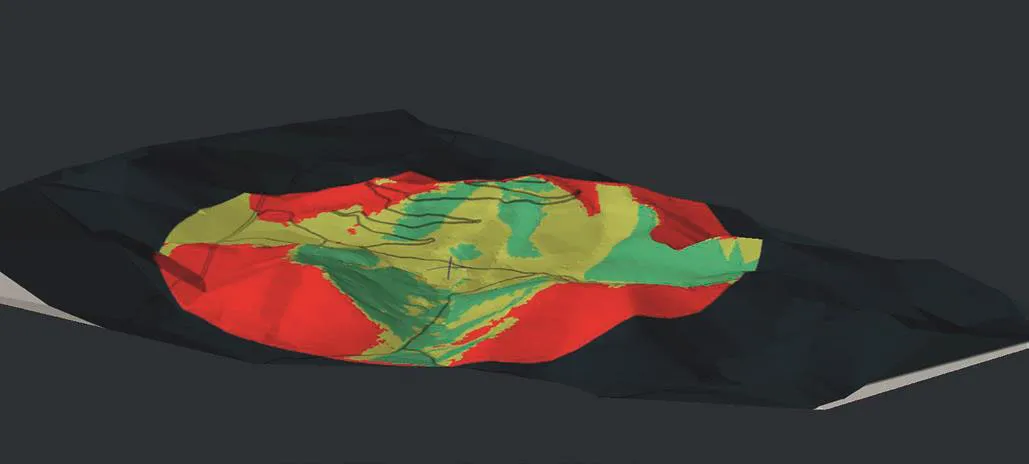
图2 视线影响区分析(红色区域不可见，黄色区域部分可见，绿色区域全部可见)

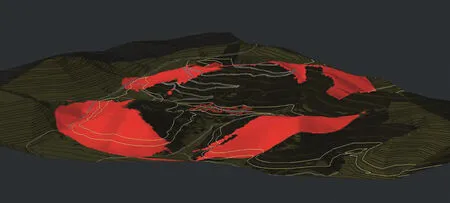
图3 边界叠加

(3)可建设范围确定：将建筑可视域范围与等高线确定的边界进行叠加，得到更精准的边界，进一步限定可建设范围(图3)。

2)建筑密度计算。

建筑密度是获得建筑占地面积的关键技术指标。风景区建筑密度的控制指标不能借鉴城乡规划的相关指标，二者环境背景不一样，因此不具有可比性。为此，研究小组专门针对江浙一带传统优秀建筑展开调研，通过获取的电子数据结合现场调研结果，采用同样的方法，归纳计算相似条件的建筑及建筑群的建筑密度(表1)，得出建筑密度(ρ)的可参照区间为0≤ρ≤0.25，可将其代入公式(建筑占地面积=可建设面积×建筑密度)计算建筑占地面积数值区间。

2.2 控制建筑高度的算法

在风景建筑尺度控制的传统理念中，有清代施闰章所描述的“补形”思想，也有如李渔所追求的“增益”思想：“因其高而愈高之，竖阁磊峰于峻坡之上，因其卑而愈卑之，穿塘凿井于下湿之区。[12]”二者都属于因山构室以求“增补互益”的理念。这一思想对于建筑高度的控制有着模糊的制约，其基本理念都是在视觉感知下充分考虑山体形态的连续与完整以及建筑在空间格局中的隐藏与凸显。本文以Civil 3D提取山地坡形，通过参数化计算得出建筑高度的控制指标。

1)基于坡形的建筑高度限制计算(图4)：通过场地竖向信息的采集，建立数字地形模型。基于建筑选址展开分析，首先经过某一观景驻点和建筑选址中心点创建并提取纵断面。在纵断面中连接观景驻点与背景山体最高点，构建虚拟坡形线，过建筑中心位置做虚拟坡形线的垂直交线，得到基于坡形的建筑限制高度。

2)在纵断面中，通过上述辅助线获取的坡形限高高度，受所创建的纵断面曲线曲率及其变化的影响。在风景环境中，可基于规划平面选取合适的驻点位置以提取纵断面，驻点涵盖近景、中景、远景的观赏视距(图5)。设置多处驻点并求其最小值(对景观环境的影响最小)，以确保所得建筑高度满足多个观赏角度下的尺度要求。

3)利用坡形限高比计算建筑高度。传统风景建筑的高度在增补互益的观念下，或强调坡形的连续起伏，或在高处增补凸显。因此，坡形限高并不等于建筑的真实高度，需要对计算出的坡形限高进行参数化修正计算。将建筑高度与基于坡形线的建筑限制高度的比值定义为坡形限高比(F)，作为建筑高度控制的指标参数，用于描述视野范围内建筑高度对山体坡形的影响。通过提取模型中的多个纵断面分析得到多个坡形限高高度，进而选取以最小值计算得到建筑坡形限高高度Hi的区间，提出坡形限高比计算公式：

F=H/Hi

式中，F为坡形限高比；H为建筑高度；Hi为建筑坡形限高高度。

坡形限高比的参数区间是通过对类似条件下优秀传统建筑的选取与数据分析得到的。调研并归纳相似环境条件下的案例(表2)，可得到坡形限高比F的区间为[0.45，1.55]，以计算建筑高度(H)区间。通过坡形限高比可以看出建筑高度对山体坡形的影响。虽案例有限，但基本可以看出相对于坡形限高上下50%的变化幅度，可以认为，在传统理念与观赏视角下，建筑的隐与显大多为半遮半掩状态，基本符合通常对建筑尺度控制的理念。

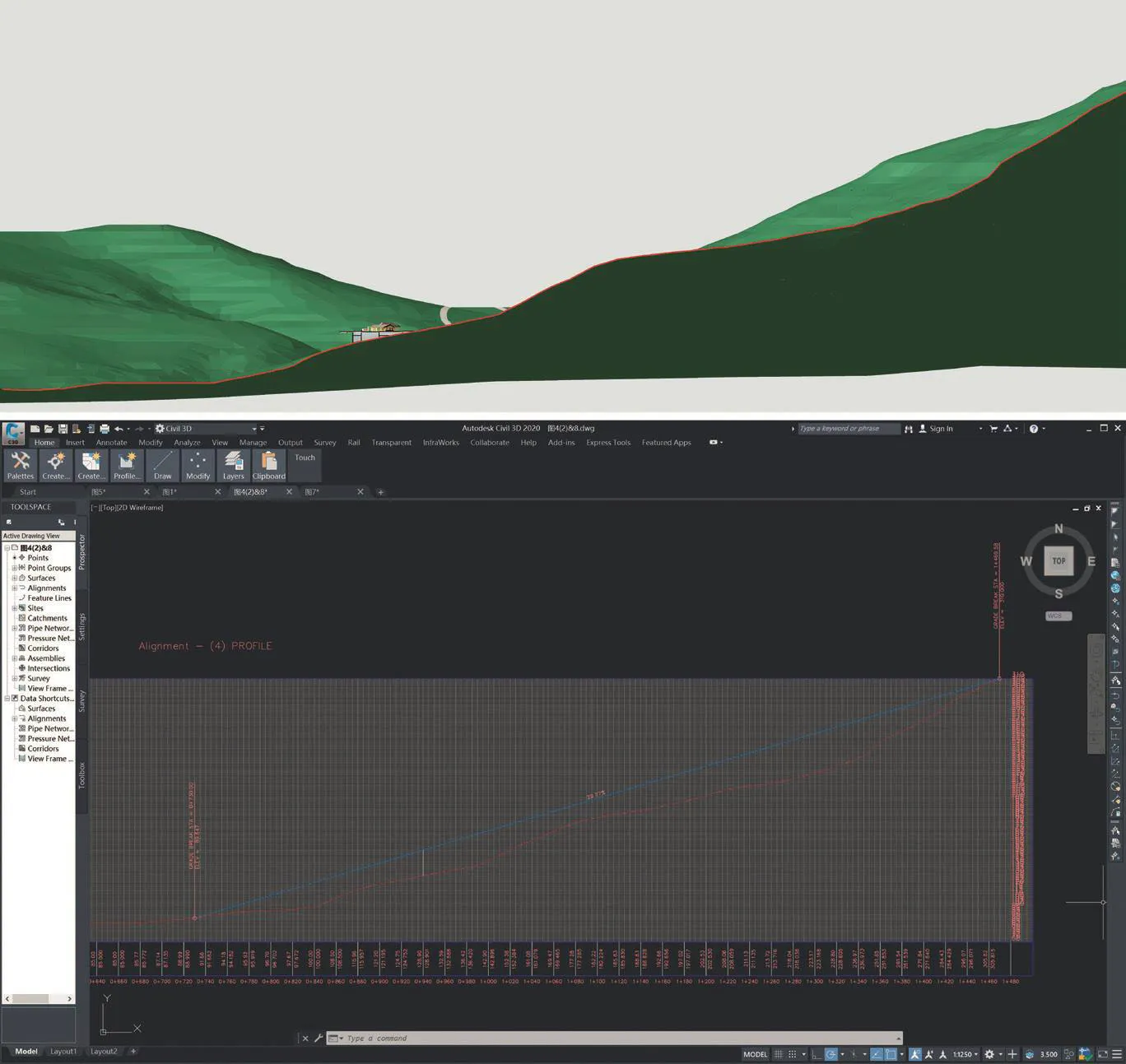
图4 Civil 3D纵断面模型分析

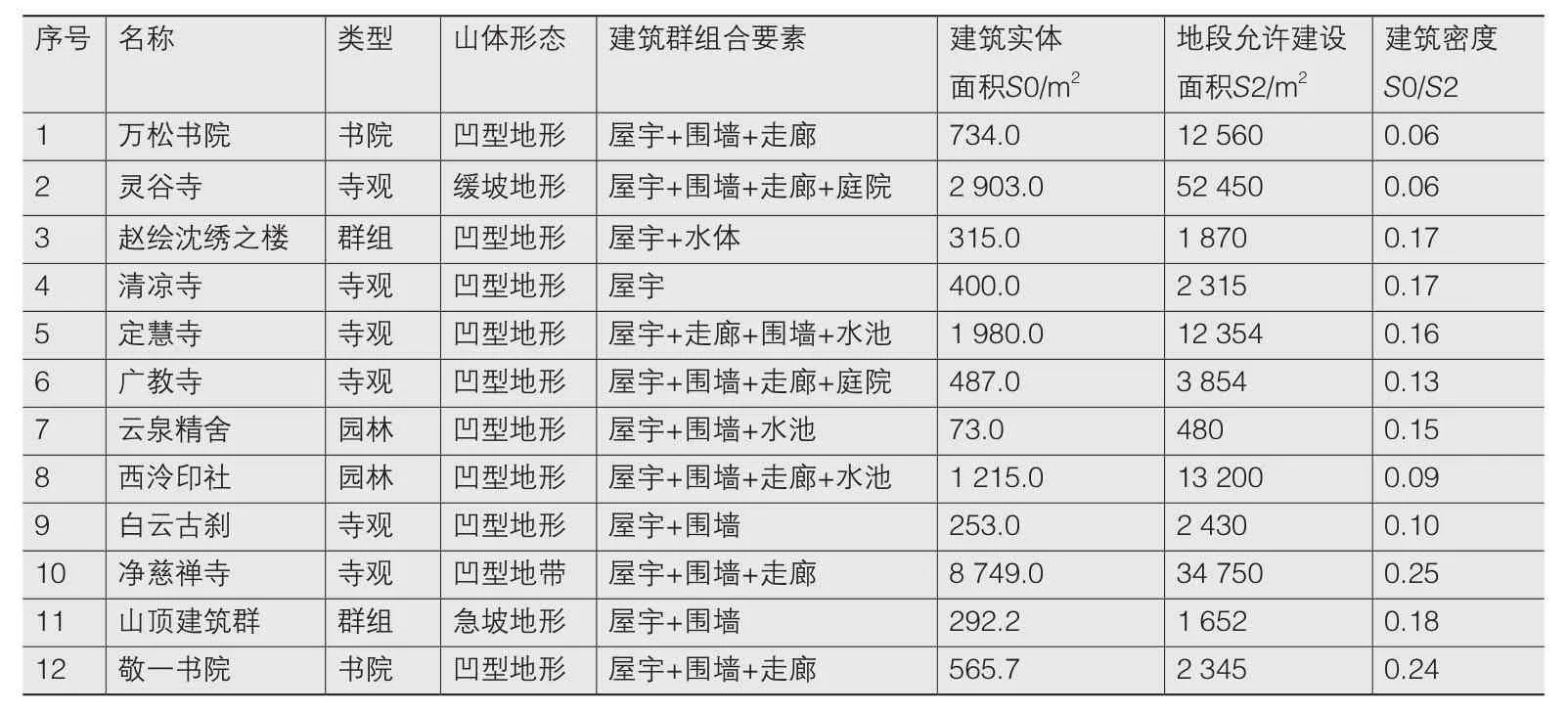
表1 相似条件建筑调研数据

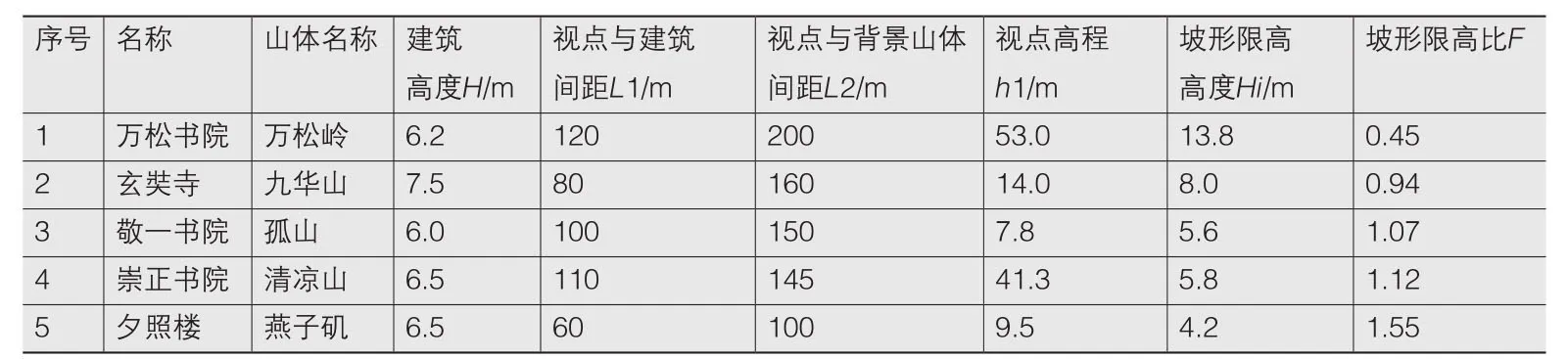
表2 区间地带坡形限高比

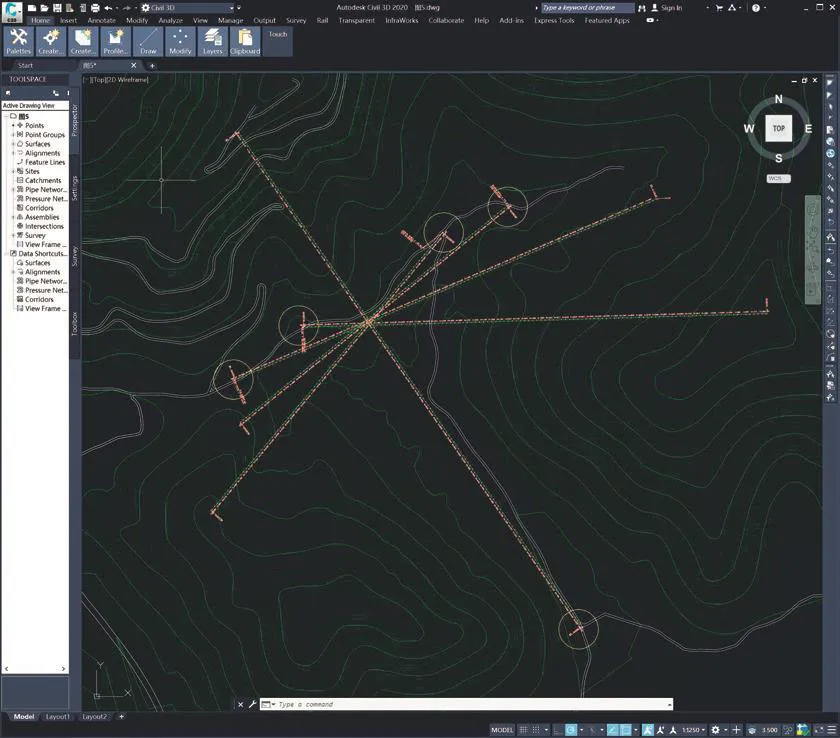
图5 设置多处驻点进行纵断面创建

图6 南京老山风景区卫星图

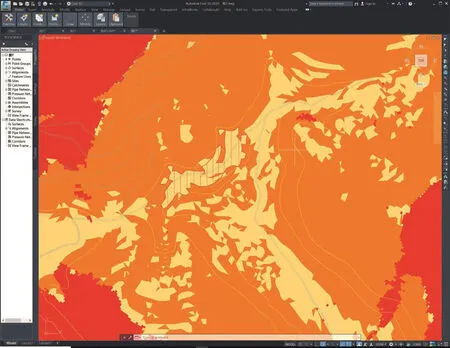
图7 可建设面积与等高线及不可视域的叠合

图8 多角度纵断面分析

3 应用研究

南京老山风景区是南京城市总体规划确定的13片环境风貌保护区之一，老山国家森林公园是其中的核心部分。在公园中，有一处位于3座山峰之间的山间平台(图6)，拟在地块东侧结合原南宋状元张孝祥的雕像形成草坪广场，地块西侧构建一座穿插迂回的状元廊，廊内设竹简铭墙，同时拥有展示、售卖、公共卫生间和观景等功能，将成为状元广场上的核心景观建筑。该建筑体量应当与山体环绕的空间相协调，通透的体量既成为一处观景胜地，又构成一处绝佳风景。在建筑选址、道路流线确定的情况下，基于Civil 3D的两大算法成为研究建筑体量的重要工具。

1)建筑占地面积的计算。

首先提取高程信息建立数字地形模型(曲面)，并将道路部分的设计图纸叠加于模型上，标识出建筑初步选址范围。将可建设坡度阈值设定为0～25%，更改曲面样式显示坡度变化，提取建筑选址范围内适于建设的坡度边界，得出区域内可建设面积S。利用Civil 3D判断建筑初步选址位置的所在高程(高程=125m)，选择坡度适合的相邻2根等高线(高程分别为115、135m)构成边界，形成建筑选址区域。设定选址处6m高度的位置进行视线影响区分析，生成建筑可视域与不可视域，叠加并细化建筑选址范围，得到区域可建设用地总面积30 415.76m2。根据建筑密度(ρ)的数值区间[0，0.25]，可得到在该选址位置处建筑占地面积(m2)数值的控制区间为[0，7 603.940](图7)。

2)建筑高度的计算。

在建筑选址位置周边的主要游览道路上设置近、中、远共5个观赏驻点，进行纵断面分析(图8，表3)，综合考虑建筑在近景、中景以及远景的眺望尺度下最合理的高度区间。观赏驻点为近景2处、中景2处、远景1处，分别通过驻点与建筑选址位置做5个纵断面，并利用Civil 3D进行分析，得到对应的坡形限高高度，利用Excel进行数据整理求其最小值。结合调研得到的坡形限高比F的参数值区间为[0.45，1.55]，利用公式H=F×Hi，对建筑高度H的区间范围进行计算。得出在该选址位置处建筑高度(m)数值的控制区间应为[5.5，18.6]。基于环境容量的考虑，建筑高度实际只要低于18.6m，对环境的影响都是可以承受的，且越接近底线越好。其中5.5m为参数计算的最低值，实际上如果低于此高度，表示在某些可视域内无法看到，对环境影响自然更小。

3)建筑体量及设计调整。

通过计算，可获得建筑的大致体积(m3)区间[0，141 432.5]，实际设计的状元廊建筑体量为6 198.9m3，在计算得到的控制区间内。在设计控制的系列指标中，考虑到建筑高度控制区间的最高值从燕子矶夕照楼采集而来，属于垂直体量的建筑类型，与本方案建筑类型有较大差异，因此将建筑高度(m)数值控制区间调整为[5.5，13.6]，且建筑选址位于陡坡边缘，视觉彰显度较大，因此结合高差变化，最终将建筑最高高度确定为10.2m(局部跌落)，大部分高度在4.2～7.3m，基本都在基于坡形限高比得出的建筑高度限制区间[5.5，13.6]内；建筑占地总面积659m2，观景平台占地460m2，在计算出的建筑占地面积区间[0，7 603.9]内，大部分可用区域最终建设成为广场和草坪。

在设计中，考虑到建筑体量数值偏于计算出的空间容量下限，因此实际建筑体量具有了较大弹性。在布局中通过回转曲廊的方法，围合出面向广场和面向山谷的两大开放空间，形成了空间与流线互相穿插的折线空间；在建筑体量的调整中，以计算出的限高下限为准，建筑物以一层高度为主，并利用场地的竖向高差，形成高低错落的建筑形态。考虑到面向山谷的景观面的开敞度，整个建筑体量布局偏向场地西侧，东侧以观景平台及以张孝祥雕塑为主的大面积草坪相呼应。建筑以廊道形式为主，采用木屋架结构结合混凝土支撑结构，在廊内设置可旋转的竹简铭墙，彰显状元文化的特色与底蕴。在连续变化的通透长廊中，利用局部空间的变化，融入相对封闭的售卖、卫生间等功能，构成了以状元文化为底蕴的老山国家森林公园中的重要景点(图9、10)。

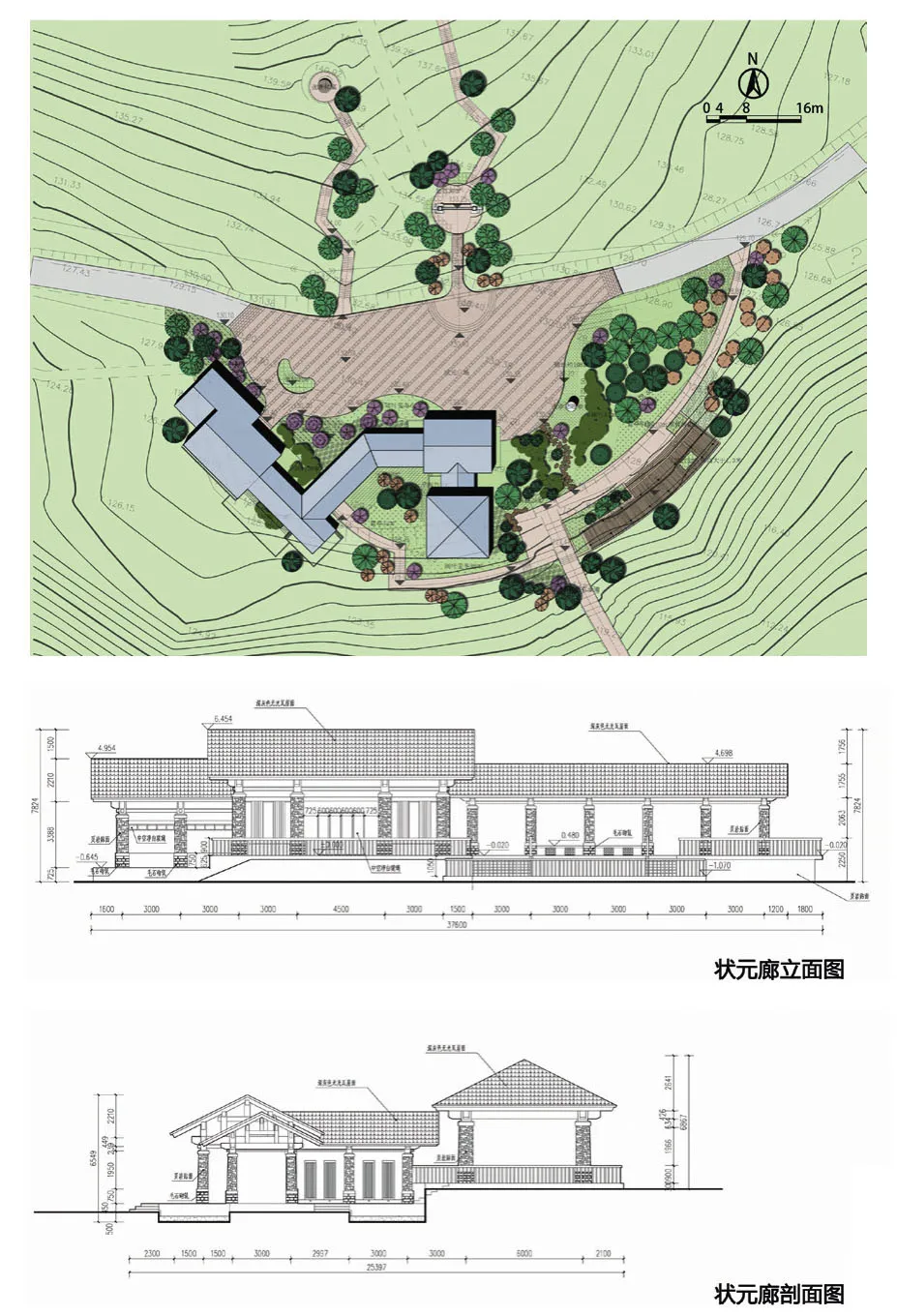
图9 老山状元廊技术图纸

图10 老山状元廊实景

表3 各纵断面建筑坡形限高高度统计

4 结语

从传统模糊的体量控制理念到参数化计算，相较于经验、感性的控制理念更为科学、合理。基于Civil 3D计算的体量控制技术是一次有益的尝试，其中等高线与坡断面的自动提取功能是其优势。在结合传统理念的基础上，不仅具有清晰可调控的技术手段，而且能兼顾多种设计方向，兼顾不同建筑类型，具有可调节的弹性区间。需要强调的是，参数化计算方法只是通过科学计算找到了基于环境特征的最大承载量，在实际操作上应尽量取建筑控制高度的最小值，这样才能使整体环境更加贴近自然。