对2019年高考全国ⅠⅠ卷理科21题的溯源与解析*

福建省南平市高级中学(353000) 江智如

2019年高考全国ⅠⅠ卷理科第21 题,题型结构常见,三个问题按梯度层层递进,难度步步提升,很好地考查考生的推理论证能力与运算求解能力,体现试题的区分功能与选拔功能.因为高考试题通常都具有深刻的命题背景,所以作为一线数学教师,不能仅限于解题和就题论题,而应站在命题者的角度探寻试题命制的源流,追溯问题的本源[1],更好地理解与领悟课程标准的精神[2]和要求,提高日常教学的质量与效率.

1 试题呈现

题目(2019年高考全国ⅠⅠ卷理科第21 题) 已知点A(-2,0),B(2,0),动点M(x,y) 满足直线AM与BM的斜率之积为记M的轨迹为曲线C.

(Ⅰ)求C的方程,并说明C是什么曲线；

(ⅠⅠ)过坐标原点的直线交C于P,Q两点,点P在第一象限,PE⊥x轴,垂足为E,连结QE并延长交C于点G.

(i) 证明：△PQG是直角三角形；

(ii) 求△PQG面积的最大值.

本试题三个小问,按照“轨迹—证明—求值”常规结构命制,第(Ⅰ)问求轨迹是利用椭圆的“第三定义”—斜率乘积为定值求解；第(i)问是常见俗套问题-“垂直”问题；第(ii)问是在第(i)问的基础上求最值问题,全题波澜不惊,步步为营,让人似曾相识,下面笔者探寻试题的本源与解法.

2 试题溯源

笔者查阅历年高考试题,发现本试题几乎是2011年江苏高考第18 题的原题,试题如下：

题1 (2011年高考江苏卷第18 题) 如图1,在平面直角坐标系xoy中,M,N分别是椭圆的顶点,过坐标原点的直线交椭圆于P,A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k.

(Ⅰ)当直线PA平分线段MN时,求k的值；

(ⅠⅠ)当k=2 时,求点P到直线AB的距离；

(ⅠⅠⅠ) 对 任 意k＞0,求 证：PA⊥PB.

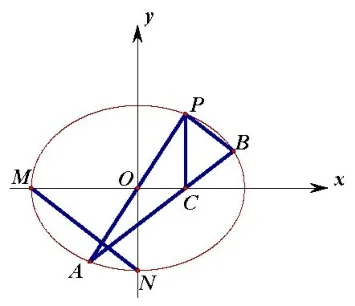
图1

点评题1 与全国ⅠⅠ卷第21 题的已知条件非常相似,区别在：题1 中曲线方程直接给出,而全国ⅠⅠ卷的试题则把曲线方程设置为第(Ⅰ)问进行求解,两道试题考查的难点都是“垂直”问题.此外,题1 的第(Ⅰ)问和第(ⅠⅠ)问设置比较基本,面对大部分考生,难度比全国ⅠⅠ卷试题低；全国ⅠⅠ卷试题第(Ⅰ)问利用斜率定义求解曲线方程,属于概念题型,大部分考生能够完成,但从第(ⅠⅠ)问开始难度提高.整体上看,两道试题考查的目标与解题思路一致,都是考查曲线轨迹知识与解析几何相关知识,考查考生数学阅读水平,数形结合思想、推理论证能力和运算求解能力.

除了题1 相似外,笔者发现2012年湖北高考理科第21题也是此类题型,只是把x轴与y轴交换一下而已,试题如下：

题2 (2012 湖北理21)设A是单位圆x2+y2=1 上的任意一点,l是过点A与x轴垂直的直线,D是直线l与x轴的交点,点M在直线l上,且满足|DM|=m|DA|(m＞0且m/=1).当点A在圆上运动时,记点M的轨迹为曲线C.

(Ⅰ)求曲线C的方程,判断曲线C为何种圆锥曲线,并求其焦点坐标；

(ⅠⅠ)过原点且斜率为k的直线交C于P,Q两点,其中点P在第一象限,它在y轴上的射影为N,直线QN交曲线C于另一点H.是否存在m,使对任意的k＞0,都有PQ⊥PH? 若存在,求m的值；若不存在,请说明理由.

点评题2 引入参数,讨论轨迹方程,考查椭圆的定义与几何性质知识,考查考生分类讨论思想和运算求解能力.如图2,第(ⅠⅠ)问在第(Ⅰ)问的基础上,探究PQ⊥PH成立所需的值,虽然已知条件把x轴换成y轴,但是解题思路与全国ⅠⅠ卷和江苏卷试题一脉相承,解题方法殊途同归.

考查直线与椭圆位置关系的相关知识,考查考生数形结合思想、推理论证能力和运算求解能力,同时题2 与全国ⅠⅠ卷第21 题在试卷中的定位类似,都是作为压轴题,体现试题的区分功能与选拔功能.

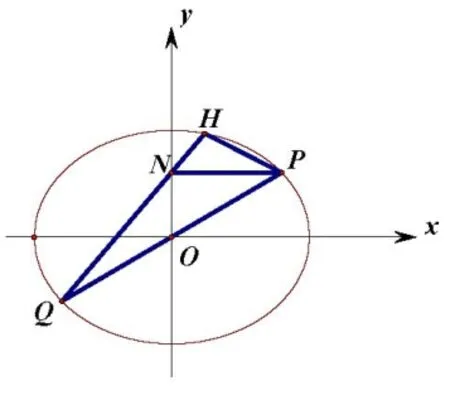
图2

3 试题解析

3.1 试题分析

试题的第(Ⅰ)问是常见的求轨迹题型,面向大部分的考生,考生只要按照日常复习的“轨迹问题五步骤”就可顺利求解.第(i)问的本质是垂直问题,常用“斜率法”或“向量法”求解,考查一元二次方程韦达定理知识,计算量大,考查考生的运算求解能力.第(ii)问是在第(i)问的基础上,求解三角形面积的表达式,利用“对勾”函数的性质及单调性求解最大值.其中,如何建立三角形面积的表达式是本小问的难点,考查考生推理论证与运算求解能力,计算复杂,难度大,考查考生综合数学能力与素养,体现试题的区分功能与选拔功能.

3.2 试题解析

(Ⅰ) 直 线AM的 斜 率 为：BM的斜率为：则化简得所以曲线C的方程为是焦点在x轴上,不包含A,B两顶点的椭圆.

(ⅠⅠ) (i)如图3,由已知可设直线PQ方程为：y=kx,(k＞0),代入曲线C:x2+2y2=4,得x2=因为点P在第一象限,所以xP=从而

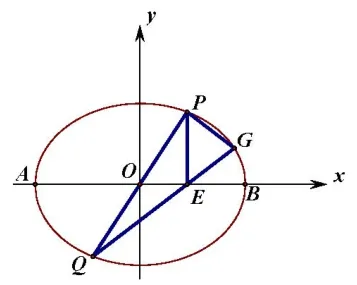
图3

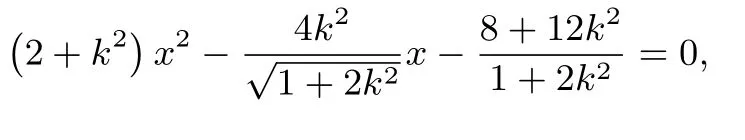
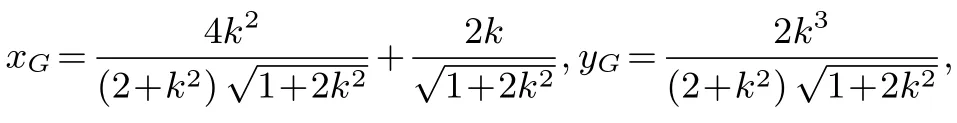
(ii)由(i)知

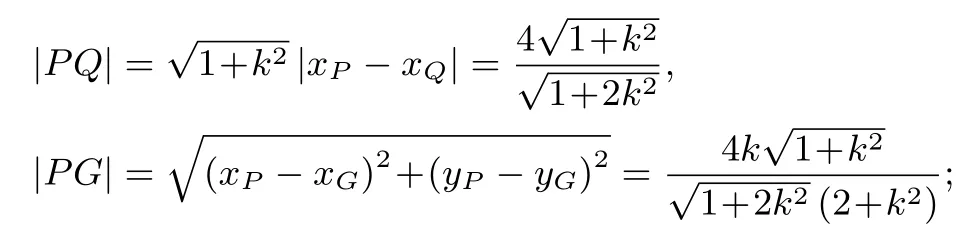
故

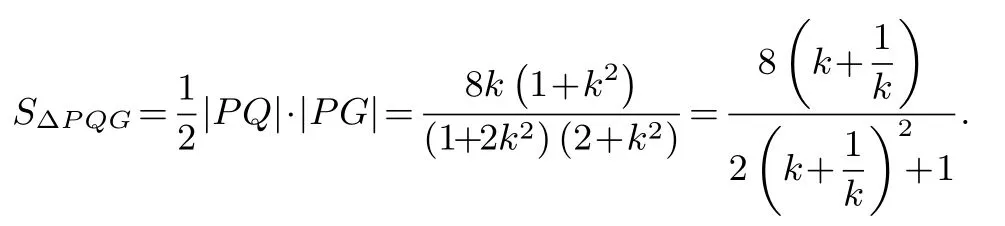
令t=则t ≥2,从而因为在[2,+∞)上单调递增,所以当t=2 即k=1 时,S△PQG最大值为因此△PQG面积的最大值为

3.3 试题点评

本试题较往年的高考试题,固本强基,夯实基础,难度有所回归,技巧性强,运算复杂,计算量大,把解析几何的特点展现得淋漓尽致,突出区分功能和选拔功能.试题将椭圆、动点的轨迹、两直线垂直、函数最值等知识内容有机结合,考查考生运用数形结合的思想方法和综合应用数学知识解决问题的能力,对数学阅读能力、逻辑推理能力、运算求解能力有较高的要求[3].试题重基础、重能力,稳中有变,在不变中蕴含着变,符合《课程标准》和《考试大纲》的要求,破解应试教育,对引领数学课程改革能起到正确的导向作用,不失为一道好题.

4 溯源启示

4.1 转变教学视角

随着新一轮高中课程改革的实施,教师对解析几何的教学应由传统的“结果性教学”转变为素养立意的“过程性教学”,这就要求教师在教学过程中,不仅要让学生知其然,更要知其所以然,同时引导学生了解甚至主动去探究解析几何问题的本“源”,学会举一反三,而不是就题解题,机械模仿.一方面,教师探寻解析几何问题的本“源”,追溯数学思维发展的源泉,可以提升教师自身数学专业素养和专业化水平；另一方面,教师把握解析几何问题的“流”[4],可以培养学生多维度思考问题的习惯,登高望远,拓展视野.

如全国ⅠⅠ卷的第(ⅠⅠ)问,能够培养学生思维的深度和广度,提高学习数学的兴趣,挖掘数学学习的潜能.

4.2 设置精致练习

考试对教学有导向功能,影响教师教学的深度和广度.2019年高考《考试大纲》明确“了解曲线与方程的对应关系,理解数形结合的思想,了解圆锥曲线的简单应用”考查目标,以及“基础性、综合性、应用性、创新性”四个考查要求[1].在日常解析几何教学中,教师应按照《课程标准》和《考试大纲》的要求,从学生的认知发展规律出发,设置精致练习[5],摒弃“题海战术”,以解析几何知识与能力为载体,突出学科素养导向,注重学生直观想象素养与逻辑推理素养的培养,使习题有“源”而“活”,有“源”而“新”,让学生在“润物细无声”中[6]理解与掌握解析几何知识,提升数学应用能力.